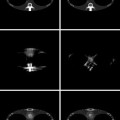
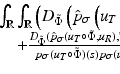: the mesh, namely, a set of triangles
v: current mesh vertex to be denoised
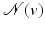 : neighborhood of vertex v (this neighborhood excludes v).
: neighborhood of vertex v (this neighborhood excludes v).n v , n p , etc.: normals at vertex v or point p, etc., to the underlying surface
w 1( | | p − v | | ), w 2( < n v , p − v > ), etc.: 1D centered Gaussians with various variances, used as weighting functions applied to the distance of neighbors to the current vertex and to the distance along the normal direction at v.
H v , H p , etc.: curvatures of the underlying surface at v, p, etc.
f: triangle of a mesh
a f : area of triangle f
c f : barycenter of triangle f
n f : normal to triangle f
Π f : projection on the plane containing triangle f
V: voxel containing points of the data set
s ′ , 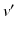 ,
, 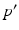 ,
, 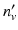 : processed versions of s, v, p, n v , etc.
: processed versions of s, v, p, n v , etc.
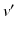 ,
, 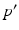 ,
, 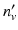 : processed versions of s, v, p, n v , etc.
: processed versions of s, v, p, n v , etc.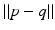 : Euclidean distance between points p and q
: Euclidean distance between points p and q The neighborhood filter or sigma filter is attributed to Lee [26] in 1983 but goes back to Yaroslavsky and the Sovietic image processing theory (see the book summarizing these works [44]) in 2D image analysis. A recent variant by Tomasi and Manduchi names it bilateral filter [37]. The bilateral filter denoises a pixel by using a weighted mean of its similar neighbors gray levels. In the original article, the similarity measure was the difference of pixel gray levels, yielding for a pixel v of an image I with neighborhood  :
:
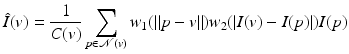 where w 1 et w 2 are decreasing functions on
where w 1 et w 2 are decreasing functions on 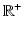 (e.g., Gaussian) and C(v) is a normalizing coefficient:
(e.g., Gaussian) and C(v) is a normalizing coefficient: 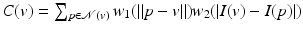 . Thus
. Thus 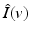 is an average of pixel values for pixels that are similar in position but also in value, hence the “bilaterality.”
is an average of pixel values for pixels that are similar in position but also in value, hence the “bilaterality.”
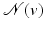 :
: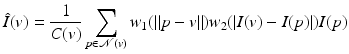
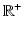 (e.g., Gaussian) and C(v) is a normalizing coefficient:
(e.g., Gaussian) and C(v) is a normalizing coefficient: 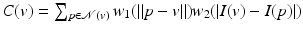 . Thus
. Thus 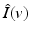 is an average of pixel values for pixels that are similar in position but also in value, hence the “bilaterality.”
is an average of pixel values for pixels that are similar in position but also in value, hence the “bilaterality.”Bilateral Filter Definitions
Filtering without losing the sharp features is as critical for surfaces as it is for images, and a first adaptation of the bilateral filter to surface meshes was proposed by Fleishman, Drori, and Cohen-Or in [15]. Consider a meshed surface 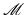 with known normals n v at each vertex position v. Let
with known normals n v at each vertex position v. Let 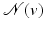 be the one-ring neighborhood of v (i.e., the set of vertices sharing an edge with v). Then the filtered position of v writes
be the one-ring neighborhood of v (i.e., the set of vertices sharing an edge with v). Then the filtered position of v writes 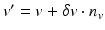 , where
, where
![$$\displaystyle{ \delta v = \frac{1} {C(v)}\sum _{p\in \mathcal{N}(v)}w_{1}(\|p - v\|)w_{2}(< n_{v},p - v >) < n_{v},p - v > }$$” src=”/wp-content/uploads/2016/04/A183156_2_En_27_Chapter_Equ1.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(1)</DIV></DIV>where the weight normalization factor is <SPAN id=IEq14 class=InlineEquation><IMG alt=]() )$$” src=”/wp-content/uploads/2016/04/A183156_2_En_27_Chapter_IEq14.gif”>. In a nutshell, this means that the normal component of the vertex v is moved by a weighted average of the normal components of its neighboring points which are also close to the plane tangent to the surface at v. The distance to the tangent plane plays for meshes the role that was played for images by the distance between gray levels. If v belongs to a sharp edge, then the only points close to the tangent plane at v are the points on the edge. Thus, the edge sharpness will not be smoothed away. One of the drawbacks of the above filter is clearly the use of a mesh-dependent neighborhood. In case of a mesh with fixed length edges, using the one-ring neighborhood is the same as using a fixed size neighborhood. Yet in most cases mesh edges do not have the same length. The one-ring neighborhood is then very dependent on the mesh representation and not on the shape itself. This is easily fixed by defining an intrinsic Euclidean neighborhood.
)$$” src=”/wp-content/uploads/2016/04/A183156_2_En_27_Chapter_IEq14.gif”>. In a nutshell, this means that the normal component of the vertex v is moved by a weighted average of the normal components of its neighboring points which are also close to the plane tangent to the surface at v. The distance to the tangent plane plays for meshes the role that was played for images by the distance between gray levels. If v belongs to a sharp edge, then the only points close to the tangent plane at v are the points on the edge. Thus, the edge sharpness will not be smoothed away. One of the drawbacks of the above filter is clearly the use of a mesh-dependent neighborhood. In case of a mesh with fixed length edges, using the one-ring neighborhood is the same as using a fixed size neighborhood. Yet in most cases mesh edges do not have the same length. The one-ring neighborhood is then very dependent on the mesh representation and not on the shape itself. This is easily fixed by defining an intrinsic Euclidean neighborhood.
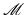 with known normals n v at each vertex position v. Let
with known normals n v at each vertex position v. Let 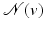 be the one-ring neighborhood of v (i.e., the set of vertices sharing an edge with v). Then the filtered position of v writes
be the one-ring neighborhood of v (i.e., the set of vertices sharing an edge with v). Then the filtered position of v writes 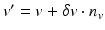 , where
, whereAnother adaptation of the 2D bilateral filter to surface meshes is introduced by Jones, Durand, and Desbrun in [20]. This approach considers the bilateral filtering problem as a robust estimation problem for the vertex position. A set of surface predictors are linked to the mesh  : for each triangle f the position estimator
: for each triangle f the position estimator  projects a point to the plane defined by f. Let a f be the surface area and c f be the center of f. Then, for each vertex v, the denoised vertex is
projects a point to the plane defined by f. Let a f be the surface area and c f be the center of f. Then, for each vertex v, the denoised vertex is
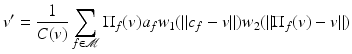
where 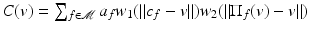 is the weight normalizing factor and w 1 and w 2 are two Gaussians.
is the weight normalizing factor and w 1 and w 2 are two Gaussians.
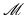 : for each triangle f the position estimator
: for each triangle f the position estimator 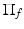 projects a point to the plane defined by f. Let a f be the surface area and c f be the center of f. Then, for each vertex v, the denoised vertex is
projects a point to the plane defined by f. Let a f be the surface area and c f be the center of f. Then, for each vertex v, the denoised vertex is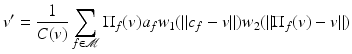
(2)
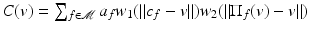 is the weight normalizing factor and w 1 and w 2 are two Gaussians.
is the weight normalizing factor and w 1 and w 2 are two Gaussians.Thus, the weight w 1( | | c f − v | | ) is small if the triangle f is close to v. This term is the classic locality-in-space term of the bilateral. Similarly, 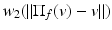 measures how far point v is from its projection onto the plane of the triangle. This weight favors the triangles f whose plane is coherent with v.
measures how far point v is from its projection onto the plane of the triangle. This weight favors the triangles f whose plane is coherent with v.
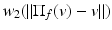 measures how far point v is from its projection onto the plane of the triangle. This weight favors the triangles f whose plane is coherent with v.
measures how far point v is from its projection onto the plane of the triangle. This weight favors the triangles f whose plane is coherent with v.Since the projection on the tangent planes operator 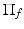 depends on the normals to f, these normals must be robustly estimated. Normals being first-order derivatives, they are more subject to noise than vertex positions. Hence the method starts by denoising the normal field. To do so, the mesh is first smoothed using the same formula as above without the influence weight w 2 and with
depends on the normals to f, these normals must be robustly estimated. Normals being first-order derivatives, they are more subject to noise than vertex positions. Hence the method starts by denoising the normal field. To do so, the mesh is first smoothed using the same formula as above without the influence weight w 2 and with 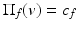 , namely, an updated position:
, namely, an updated position:
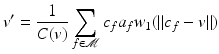 where
where 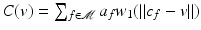 . The normal for each face in the denoised mesh is then computed and assigned to the corresponding face of the original noisy mesh. It is with this robust normal field that the bilateral filter of Eq. (2) is applied in a second step.
. The normal for each face in the denoised mesh is then computed and assigned to the corresponding face of the original noisy mesh. It is with this robust normal field that the bilateral filter of Eq. (2) is applied in a second step.
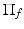 depends on the normals to f, these normals must be robustly estimated. Normals being first-order derivatives, they are more subject to noise than vertex positions. Hence the method starts by denoising the normal field. To do so, the mesh is first smoothed using the same formula as above without the influence weight w 2 and with
depends on the normals to f, these normals must be robustly estimated. Normals being first-order derivatives, they are more subject to noise than vertex positions. Hence the method starts by denoising the normal field. To do so, the mesh is first smoothed using the same formula as above without the influence weight w 2 and with 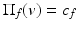 , namely, an updated position:
, namely, an updated position: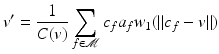
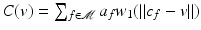 . The normal for each face in the denoised mesh is then computed and assigned to the corresponding face of the original noisy mesh. It is with this robust normal field that the bilateral filter of Eq. (2) is applied in a second step.
. The normal for each face in the denoised mesh is then computed and assigned to the corresponding face of the original noisy mesh. It is with this robust normal field that the bilateral filter of Eq. (2) is applied in a second step.The idea of filtering normals instead of point positions is crucial in point rendering applications, as was pointed out by Jones, Durand, and Zwicker in [21]. Indeed, when rendering a point set, removing noise from normal is more important than removing noise from point position, since normal variations are in fact what is perceived by observers. More precisely the eye perceives a dot product of the illumination and the normal, which makes it very sensitive to noisy normal orientations. The bilateral filter of [20] is seen as a deformation F of the points: 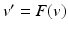 . Then, the update of normal n v can be obtained through the transposed inverse of the Jacobian J(v) of F(v):
. Then, the update of normal n v can be obtained through the transposed inverse of the Jacobian J(v) of F(v):
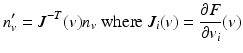 where J i is the ith column of J and v i is the ith component of v. n v must then be renormalized. The rendering of the point set with smoothed normal is better than without any smoothing.
where J i is the ith column of J and v i is the ith component of v. n v must then be renormalized. The rendering of the point set with smoothed normal is better than without any smoothing.
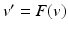 . Then, the update of normal n v can be obtained through the transposed inverse of the Jacobian J(v) of F(v):
. Then, the update of normal n v can be obtained through the transposed inverse of the Jacobian J(v) of F(v):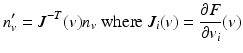
In [38], Wang introduces a related bilateral approach which denoises feature-insensitive sampled meshes. Feature insensitive means that the mesh sampling is independent of the features of the underlying surface, e.g., uniform sampling. The algorithm proceeds as follows: it detects the shape geometry (namely, sharp regions), denoises the points, and finally optimizes the mesh by removing thin triangles. The bilateral filter is defined in a manner similar to [20], with the difference that only triangles inside a given neighborhood are used on this definition. Let v be a mesh vertex, 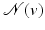 be the set of triangles within a given range of v, and n f , a f , c f be, respectively, the normal, area, and center of a facet f (a triangle). Denote by
be the set of triangles within a given range of v, and n f , a f , c f be, respectively, the normal, area, and center of a facet f (a triangle). Denote by 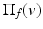 the projection of v onto the plane of f, and then the denoised vertex is defined by
the projection of v onto the plane of f, and then the denoised vertex is defined by
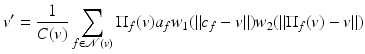 where
where 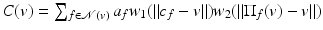 (weight normalizing factor).
(weight normalizing factor).
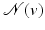 be the set of triangles within a given range of v, and n f , a f , c f be, respectively, the normal, area, and center of a facet f (a triangle). Denote by
be the set of triangles within a given range of v, and n f , a f , c f be, respectively, the normal, area, and center of a facet f (a triangle). Denote by 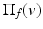 the projection of v onto the plane of f, and then the denoised vertex is defined by
the projection of v onto the plane of f, and then the denoised vertex is defined by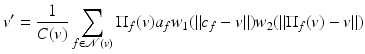
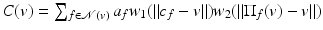 (weight normalizing factor).
(weight normalizing factor).The first step is to detect sharp regions. Several steps of bilateral filtering (as defined in [20]) are applied, and then a smoothness index is computed by measuring the infimum of angles between normals of faces adjacent to v. By thresholding this measurement, the sharp vertices are selected. Triangles whose three vertices are sharp and whose size does not increase during the bilateral iterations are marked as sharp. This detection done, points are restored to their original positions. Then the bilateral filtering formula is applied to sharp vertices only, and the geometry sharpness is encoded into a data collection containing normals, centers, and areas of filtered triangles. Points are then restored to their original position. Each sharp vertex is moved using the bilateral filtering over the neighboring stored data units, and thin vertices are removed from the mesh (these last two steps are iterated a certain number of times). Finally, a post-filtering step consists in applying one step of bilateral filtering on all non-sharp edges.
In [40] (Wang, Yuan, and Chen), a two-step denoising method combines the fuzzy C-means clustering method (see Dunn’s article on fuzzy means [12]) with a bilateral filtering approach. Fuzzy C-means is a clustering technique that allows a piece of data to belong to two different clusters. Each point p gets a parameter μ p, k which measures the degree of membership of p to a cluster k. Let m p be the number of points in the spherical neighborhood of a point p. If m p < threshold, the point is deleted. Otherwise, a fuzzy C-means clustering center c p is associated with p. The normal at point c p is computed as the normal to the regression plane of the data set in a spherical neighborhood of p. Fleishman’s bilateral filter [15] is used to filter c i which yields the denoised point. This hybrid and complex method is doubly bilateral. Indeed, the previous C-means clustering selects an adapted neighborhood for each point and replaces it by an average which is by itself the result of a first bilateral filter in the wide sense of neighborhood filter. Indeed, the used neighborhood for each point depends on the point. The second part of the method therefore applies a second classical bilateral method to a cloud that has been filtered by a first bilateral filter.
The bilateral filtering idea was also used as a part of a surface reconstruction process. In [30], for example, Miropolsky and Fischer introduced a method for reducing position and sampling noise in point cloud data while reconstructing the surface. A 3D geometric bilateral filter method for edge-preserving and data reduction is introduced. Starting from a point cloud, the points are classified in an octree, whose leaf cells are called voxels. The voxel centers are filtered, representative surface points are defined, and the mesh is finally reconstructed. A key point is that the denoising depends on the voxel decomposition. Indeed, the filter outputs a result for each voxel. For a voxel V, call v its centroid with normal n v . Let w 1 and u 2 be two functions weighting, respectively, 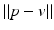 , the distance between a point p position and the centroid location, and
, the distance between a point p position and the centroid location, and 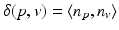 , the scalar product of the normal at p and the normal at the centroid. Then the output of the filter for voxel V is
, the scalar product of the normal at p and the normal at the centroid. Then the output of the filter for voxel V is
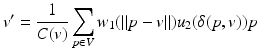 where
where 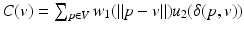 . Here w 1 is typically a Gaussian and u 2 is an increasing function on [0, 1]. But this filter proves unable to recover sharp edges, so a modification is introduced: prior to any filtering for each voxel V, points of V are projected onto a sphere centered at the centroid v. Each mapped point is given a normal
. Here w 1 is typically a Gaussian and u 2 is an increasing function on [0, 1]. But this filter proves unable to recover sharp edges, so a modification is introduced: prior to any filtering for each voxel V, points of V are projected onto a sphere centered at the centroid v. Each mapped point is given a normal 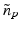 which has direction p − v and is normalized. The geometric filtering is reduced to
which has direction p − v and is normalized. The geometric filtering is reduced to
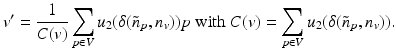 Although only the similarity of normals is taken into account in the above formula, the filter is bilateral because the average is localized in the voxel.
Although only the similarity of normals is taken into account in the above formula, the filter is bilateral because the average is localized in the voxel.
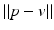 , the distance between a point p position and the centroid location, and
, the distance between a point p position and the centroid location, and 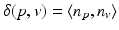 , the scalar product of the normal at p and the normal at the centroid. Then the output of the filter for voxel V is
, the scalar product of the normal at p and the normal at the centroid. Then the output of the filter for voxel V is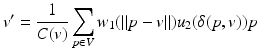
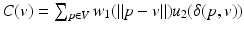 . Here w 1 is typically a Gaussian and u 2 is an increasing function on [0, 1]. But this filter proves unable to recover sharp edges, so a modification is introduced: prior to any filtering for each voxel V, points of V are projected onto a sphere centered at the centroid v. Each mapped point is given a normal
. Here w 1 is typically a Gaussian and u 2 is an increasing function on [0, 1]. But this filter proves unable to recover sharp edges, so a modification is introduced: prior to any filtering for each voxel V, points of V are projected onto a sphere centered at the centroid v. Each mapped point is given a normal 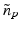 which has direction p − v and is normalized. The geometric filtering is reduced to
which has direction p − v and is normalized. The geometric filtering is reduced to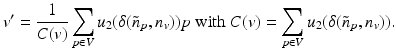
In [27], Liu et al. interpreted the bilateral filter as the association to each vertex v of a weighted average
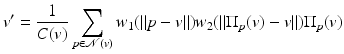 where
where 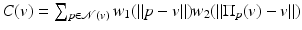 (normalizing factor) and
(normalizing factor) and 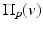 is a predictor which defines a “denoised position of v due to p,” namely, the projection of v on the plane passing by p and having the normal n v . For example, the bilateral predictor used in [15] is
is a predictor which defines a “denoised position of v due to p,” namely, the projection of v on the plane passing by p and having the normal n v . For example, the bilateral predictor used in [15] is 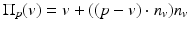 , and in [20], the used predictor is
, and in [20], the used predictor is 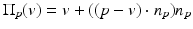 which is the projection of v on the tangent plane passing by p. With this last predictor the corners are less smoothed out, yet there is a tangential drift due to the fact that the motion is not in the normal direction n v but in an averaged direction of the n p for
which is the projection of v on the tangent plane passing by p. With this last predictor the corners are less smoothed out, yet there is a tangential drift due to the fact that the motion is not in the normal direction n v but in an averaged direction of the n p for 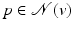 . Therefore a new predictor is introduced:
. Therefore a new predictor is introduced:
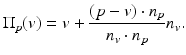 This predictor tends to preserve better the edges than all other bilateral filters.
This predictor tends to preserve better the edges than all other bilateral filters.
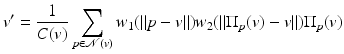
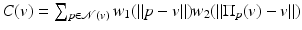 (normalizing factor) and
(normalizing factor) and 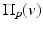 is a predictor which defines a “denoised position of v due to p,” namely, the projection of v on the plane passing by p and having the normal n v . For example, the bilateral predictor used in [15] is
is a predictor which defines a “denoised position of v due to p,” namely, the projection of v on the plane passing by p and having the normal n v . For example, the bilateral predictor used in [15] is 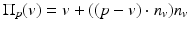 , and in [20], the used predictor is
, and in [20], the used predictor is 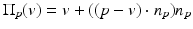 which is the projection of v on the tangent plane passing by p. With this last predictor the corners are less smoothed out, yet there is a tangential drift due to the fact that the motion is not in the normal direction n v but in an averaged direction of the n p for
which is the projection of v on the tangent plane passing by p. With this last predictor the corners are less smoothed out, yet there is a tangential drift due to the fact that the motion is not in the normal direction n v but in an averaged direction of the n p for 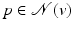 . Therefore a new predictor is introduced:
. Therefore a new predictor is introduced: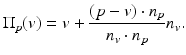
The question of choosing automatically the parameters for the bilateral filter was raised by Hou, Bai, and Wang in [19]. It was proposed to choose adaptive parameters. The adaptive bilateral normal smoothing process starts by searching for the set of triangles (T i ) i whose barycenters are within a given distance of a center triangle T. (But this keeps a distance parameter anyway.) Then the influence weight parameter σ s is computed as the standard deviation of the distance between normals 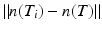 . The spatial weight parameter is estimated using a minimum length descriptor criterion (for various scales). The estimated parameters are then used to get the smoothed normal. This result is finally used for rebuilding the mesh using the smoothed normals by Ohtake, Belyaev, and Seidel’s method described in [31].
. The spatial weight parameter is estimated using a minimum length descriptor criterion (for various scales). The estimated parameters are then used to get the smoothed normal. This result is finally used for rebuilding the mesh using the smoothed normals by Ohtake, Belyaev, and Seidel’s method described in [31].
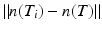 . The spatial weight parameter is estimated using a minimum length descriptor criterion (for various scales). The estimated parameters are then used to get the smoothed normal. This result is finally used for rebuilding the mesh using the smoothed normals by Ohtake, Belyaev, and Seidel’s method described in [31].
. The spatial weight parameter is estimated using a minimum length descriptor criterion (for various scales). The estimated parameters are then used to get the smoothed normal. This result is finally used for rebuilding the mesh using the smoothed normals by Ohtake, Belyaev, and Seidel’s method described in [31].The bilateral filter has proved to be very efficient to denoise a mesh while preserving sharp features. The trilateral filter is then a natural extension which takes into account still more geometric information.
Trilateral Filters
Choudhury and Tumblin [6] propose an extension of the trilateral image filter to oriented meshes. It is a 2-pass filter: a first pass filters the normals and a second pass filters the vertex positions. Starting from an oriented mesh, a first pass denoises bilaterally the vertex normals using the following update:
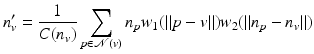 where
where 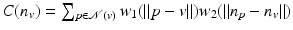 . Then, an adaptive neighborhood
. Then, an adaptive neighborhood 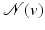 is found by iteratively adding faces near v until the normals n f of face f differ too much from n v ′ . A function F measuring the similarity between normals is built using a given threshold R:
is found by iteratively adding faces near v until the normals n f of face f differ too much from n v ′ . A function F measuring the similarity between normals is built using a given threshold R:
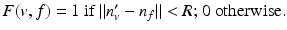
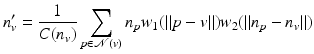
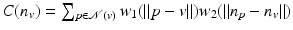 . Then, an adaptive neighborhood
. Then, an adaptive neighborhood 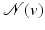 is found by iteratively adding faces near v until the normals n f of face f differ too much from n v ′ . A function F measuring the similarity between normals is built using a given threshold R:
is found by iteratively adding faces near v until the normals n f of face f differ too much from n v ′ . A function F measuring the similarity between normals is built using a given threshold R: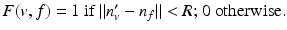
The trilateral filter for normals filters a difference between normals. Define 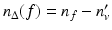 . Then the trilaterally filtered normal n v is
. Then the trilaterally filtered normal n v is
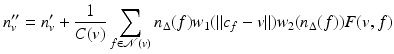 where
where 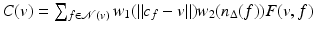 . Finally, the same trilateral filter can be applied to vertices. Call P v the plane passing through v and orthogonal to n v ′ . Call
. Finally, the same trilateral filter can be applied to vertices. Call P v the plane passing through v and orthogonal to n v ′ . Call 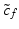 the projection of c f onto P v and
the projection of c f onto P v and 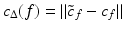 . Then the trilateral filter for vertices, using the trilaterally filtered normal n v ′ ′ , writes
. Then the trilateral filter for vertices, using the trilaterally filtered normal n v ′ ′ , writes
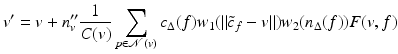 where
where 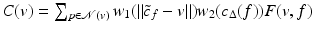 .
.
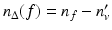 . Then the trilaterally filtered normal n v is
. Then the trilaterally filtered normal n v is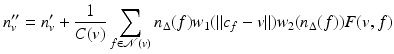
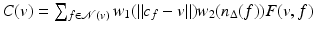 . Finally, the same trilateral filter can be applied to vertices. Call P v the plane passing through v and orthogonal to n v ′ . Call
. Finally, the same trilateral filter can be applied to vertices. Call P v the plane passing through v and orthogonal to n v ′ . Call 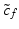 the projection of c f onto P v and
the projection of c f onto P v and 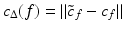 . Then the trilateral filter for vertices, using the trilaterally filtered normal n v ′ ′ , writes
. Then the trilateral filter for vertices, using the trilaterally filtered normal n v ′ ′ , writes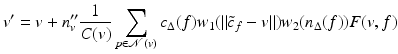
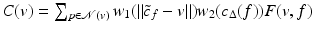 .
.Similarity Filters
In [41] Wang et al. proposed a trilateral filter with slightly different principles. A geometric intensity of each sampled point is first defined as depending on the neighborhood of the point
![$$\displaystyle{\delta (p) = \frac{1} {C(p)}\sum _{q\in \mathcal{N}(p)}w_{pq} < n_{p},q - p >}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_27_Chapter_Equm.gif”></DIV></DIV></DIV>with<br />
<DIV id=Equn class=Equation><br />
<DIV class=EquationContent><br />
<DIV class=MediaObject><IMG alt=]() \|)w_{h}(\|H_{q} – H_{p}\|)}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_27_Chapter_Equn.gif”>and
\|)w_{h}(\|H_{q} – H_{p}\|)}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_27_Chapter_Equn.gif”>and
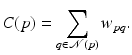
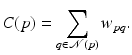
This type of filter is a trilateral filter, which means that it depends on three variables: distance between the point p and its neighbors q, distance along the normal n p between the point p and its neighbors q, and the difference of their mean curvatures H p and H q .
At each point, a local grid is built on the local tangent plane (obtained by local covariance analysis), and at each point of this grid, the geometry intensity is defined by interpolation. Thus, neighborhoods of the same geometry are defined for each pair of distinct points, and the similarity can be computed as a decreasing function of the L 2 distance between these neighborhoods.
Since the goal is to denoise one point with similar points, the algorithm proposes to cluster the points into various classes by the mean shift algorithm. To denoise a point, only points of the same class are used. This gives a denoised geometry intensity δ ′ (p) and the final denoised position 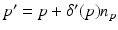 .
.
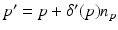 .
.More recently the NL-means (Buades, Coll, Morel [3]) method which proved very powerful in image denoising was adapted to meshes and point clouds by Yoshizawa, Belyaev, and Seidel [47]. Recall that for an image I, the NL-means filter computes a filtered value J(x) of pixel x as
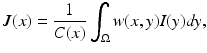 an adaptive average with weights
an adaptive average with weights
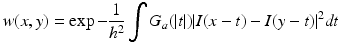 and
and 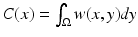 .
.
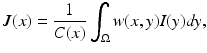
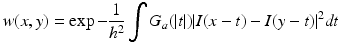
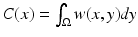 .
.