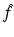(1)
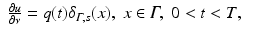
(2)
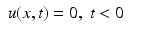
(3)
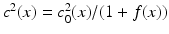 with the (known) background velocity c 0 and a function f > −1 which has to be determined.
with the (known) background velocity c 0 and a function f > −1 which has to be determined.We remark that everything we are doing in this paper can also be done for more general problems, such as problems with varying density [26], in moving media [61] and problems with attenuation [4, 20, 40].
3 The Born Approximation
Even though the underlying differential equation is linear, the inverse problem is nonlinear. Most of the literature on the problem makes use of some kind of linearization, mostly the Born approximation. Our goal is definitely to deal with the fully nonlinear problem. However linearization leads to valuable insights also for the nonlinear problem. Therefore we discuss the Born approximation in some detail.
An Explicit Formula for the Slab
We restrict ourselves to a very simple geometry: Ω is just the slab 0 < x n < D. Sources and receivers are sitting either on both boundaries (transmission mode) or on only one of them (reflection mode). It is more convenient to work with the inhomogeneous initial value problem
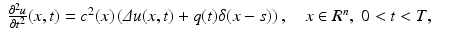
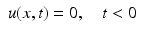
with δ the Dirac function in R n and s a source. We also assume c(x) = c 0 > 0 constant in this section. Equations (4), (5) is a simplified version of (1)–(3).
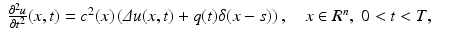
(4)
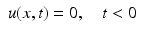
(5)
We also look at the problem in the frequency domain. For the Fourier transform in R n , we use the notation
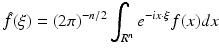 and we denote the inverse Fourier transform of f by
and we denote the inverse Fourier transform of f by 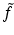 . Doing an inverse Fourier transform with respect to t in (4), we get
. Doing an inverse Fourier transform with respect to t in (4), we get
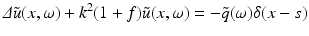
where 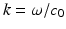 is the wave number. Because of (5) this equation has to be complemented by the Sommerfeld radiation condition for outgoing radiation, i.e.,
is the wave number. Because of (5) this equation has to be complemented by the Sommerfeld radiation condition for outgoing radiation, i.e.,
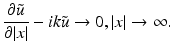 In this section we derive an explicit representation of the Born approximation by Fourier analysis. We follow [14, 42].
In this section we derive an explicit representation of the Born approximation by Fourier analysis. We follow [14, 42].
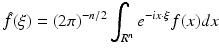
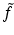 . Doing an inverse Fourier transform with respect to t in (4), we get
. Doing an inverse Fourier transform with respect to t in (4), we get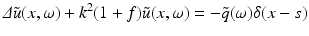
(6)
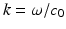 is the wave number. Because of (5) this equation has to be complemented by the Sommerfeld radiation condition for outgoing radiation, i.e.,
is the wave number. Because of (5) this equation has to be complemented by the Sommerfeld radiation condition for outgoing radiation, i.e.,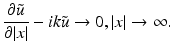
For f = 0, the solution of (6) is 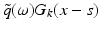 with G k the free space Green’s function which we give in the plane wave decomposition
with G k the free space Green’s function which we give in the plane wave decomposition
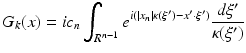
where 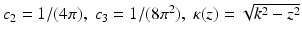 . For z > k, κ(z) is defined to be
. For z > k, κ(z) is defined to be 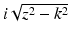 .
.
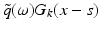 with G k the free space Green’s function which we give in the plane wave decomposition
with G k the free space Green’s function which we give in the plane wave decomposition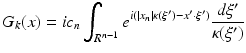
(7)
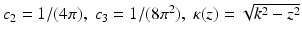 . For z > k, κ(z) is defined to be
. For z > k, κ(z) is defined to be 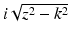 .
.For arbitrary f, we put 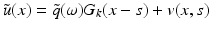 , obtaining for v
, obtaining for v
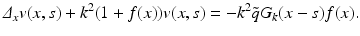 Neglecting fv leads to the Born approximation
Neglecting fv leads to the Born approximation
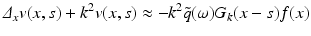 or
or
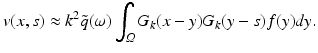 With x ′ the first n − 1 coordinates of x and correspondingly for s, y we rewrite this as
With x ′ the first n − 1 coordinates of x and correspondingly for s, y we rewrite this as
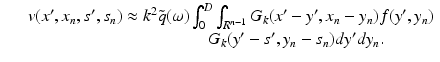 Inserting (7) we get
Inserting (7) we get
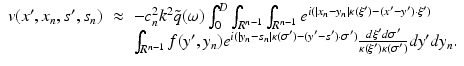 The y ′ integral is just a (n − 1)-dimensional Fourier transform, hence
The y ′ integral is just a (n − 1)-dimensional Fourier transform, hence
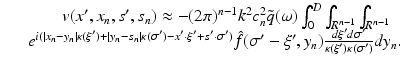
where 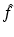 is the (n − 1)-dimensional Fourier transform of f with respect to the first n − 1 variables. Fourier transforms of dimensions n − 1 with respect to x ′ and s ′ yield
is the (n − 1)-dimensional Fourier transform of f with respect to the first n − 1 variables. Fourier transforms of dimensions n − 1 with respect to x ′ and s ′ yield
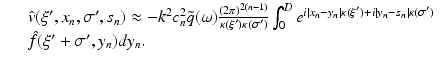 In particular we have
In particular we have
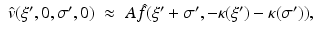
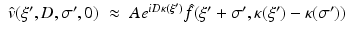
where 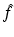 is now the n-dimensional Fourier transform of f and
is now the n-dimensional Fourier transform of f and 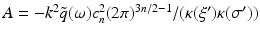 . Equations (9), (10) is the solution of the inverse problem of reflection and transmission imaging, resp., in the Born approximation. Note that the derivation of (9), (10) depends entirely on the plane wave decomposition of G k which was used first in this context in [14].
. Equations (9), (10) is the solution of the inverse problem of reflection and transmission imaging, resp., in the Born approximation. Note that the derivation of (9), (10) depends entirely on the plane wave decomposition of G k which was used first in this context in [14].
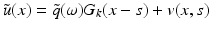 , obtaining for v
, obtaining for v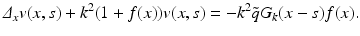
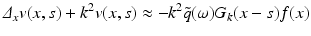
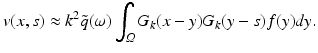
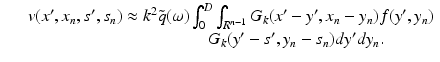
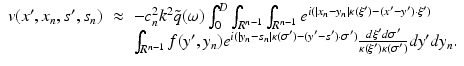
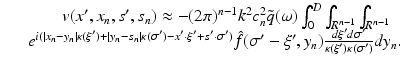
(8)
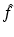 is the (n − 1)-dimensional Fourier transform of f with respect to the first n − 1 variables. Fourier transforms of dimensions n − 1 with respect to x ′ and s ′ yield
is the (n − 1)-dimensional Fourier transform of f with respect to the first n − 1 variables. Fourier transforms of dimensions n − 1 with respect to x ′ and s ′ yield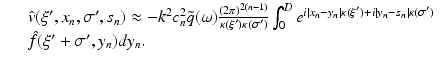
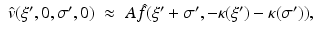
(9)
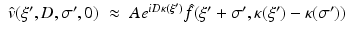
(10)
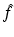 is now the n-dimensional Fourier transform of f and
is now the n-dimensional Fourier transform of f and 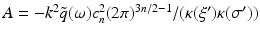 . Equations (9), (10) is the solution of the inverse problem of reflection and transmission imaging, resp., in the Born approximation. Note that the derivation of (9), (10) depends entirely on the plane wave decomposition of G k which was used first in this context in [14].
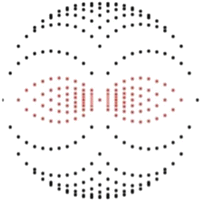
. Equations (9), (10) is the solution of the inverse problem of reflection and transmission imaging, resp., in the Born approximation. Note that the derivation of (9), (10) depends entirely on the plane wave decomposition of G k which was used first in this context in [14].Let’s look at the transmission case, i.e., (10). For simplicity, we consider the 2D case. Consider the semicircle of radius k in the upper half plane around the origin. Attach to each point of this semicircle the semicircle of radius k around this point that opens downward. According to (10), 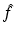 is determined by the data along each of these semicircles. These semicircles fill the circles of radius k with midpoints (±k, 0); see Fig. 1. In the reflection case (9) we proceed in the same way, except that we start out from the semicircle in the lower half plane. Now the attached semicircles fill the semicircle of radius 2k in the lower half plane, except for the circles of radius k around (±k, 0).
is determined by the data along each of these semicircles. These semicircles fill the circles of radius k with midpoints (±k, 0); see Fig. 1. In the reflection case (9) we proceed in the same way, except that we start out from the semicircle in the lower half plane. Now the attached semicircles fill the semicircle of radius 2k in the lower half plane, except for the circles of radius k around (±k, 0).
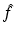 is determined by the data along each of these semicircles. These semicircles fill the circles of radius k with midpoints (±k, 0); see Fig. 1. In the reflection case (9) we proceed in the same way, except that we start out from the semicircle in the lower half plane. Now the attached semicircles fill the semicircle of radius 2k in the lower half plane, except for the circles of radius k around (±k, 0).
is determined by the data along each of these semicircles. These semicircles fill the circles of radius k with midpoints (±k, 0); see Fig. 1. In the reflection case (9) we proceed in the same way, except that we start out from the semicircle in the lower half plane. Now the attached semicircles fill the semicircle of radius 2k in the lower half plane, except for the circles of radius k around (±k, 0).
Fig. 1
Left: Fourier coverage for transmission imaging. Right: Fourier coverage for reflection imaging. k is the wave number. The figures are for n = 2. For n = 3, one has to rotate the figures around the vertical axis
Thus we see a fundamental difference between transmission and reflection imaging: In transmission imaging low frequency features f can be recovered irrespectively of the frequency content of the source pulse q, whereas in reflection imaging one needs low frequencies in the source pulse to recover low frequency features in f. This is one of the main difficulties in seismic imaging; see [9, 19, 22, 30, 60]. To the best of our knowledge, Fig. 1 appeared first in [35, 64]. The difficulties in reflection imaging without low frequencies will be discussed in section “Missing Low Frequencies”.
We also conclude from (9), (10) that combined transmission and reflection measurements determine 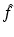 within the ball of radius 2k. In other words, since
within the ball of radius 2k. In other words, since 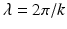 is the wavelength of the irradiating sources, the spatial resolution according to Shannon’s sampling theorem is
is the wavelength of the irradiating sources, the spatial resolution according to Shannon’s sampling theorem is 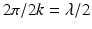 . This is a classical result already known to Born.
. This is a classical result already known to Born.
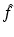 within the ball of radius 2k. In other words, since
within the ball of radius 2k. In other words, since 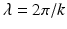 is the wavelength of the irradiating sources, the spatial resolution according to Shannon’s sampling theorem is
is the wavelength of the irradiating sources, the spatial resolution according to Shannon’s sampling theorem is 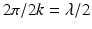 . This is a classical result already known to Born.
. This is a classical result already known to Born.The numerical evaluation of (9), (10) is by no means trivial. In principle it can be done by Fourier transforms. However this requires a sophisticated software for non-equispaced fast Fourier transforms. Assuming uniform sampling of 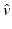 in ξ ′ and σ ′ leads to non-equispaced sampling of
in ξ ′ and σ ′ leads to non-equispaced sampling of 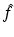 on a grid of the type shown in Fig. 2. An implementation similar to the filtered backprojection algorithm of X-ray computerized tomography has been given in [14].
on a grid of the type shown in Fig. 2. An implementation similar to the filtered backprojection algorithm of X-ray computerized tomography has been given in [14].
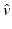 in ξ ′ and σ ′ leads to non-equispaced sampling of
in ξ ′ and σ ′ leads to non-equispaced sampling of 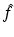 on a grid of the type shown in Fig. 2. An implementation similar to the filtered backprojection algorithm of X-ray computerized tomography has been given in [14].
on a grid of the type shown in Fig. 2. An implementation similar to the filtered backprojection algorithm of X-ray computerized tomography has been given in [14].An Error Estimate for the Born Approximation
We now assume that Ω is a ball of radius r, the background speed is constant as in the previous section, and that the illumination done is by plane waves. This leads to the problem
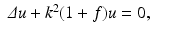
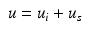
where u i = exp ikx ⋅ θ is the incoming wave with direction θ ∈ S n−1 and wave number k and u s is the scattered wave satisfying the Sommerfeld radiation condition of exterior radiation. We assume f to be supported in Ω. θ runs through all of S 1 for n = 2 and through a great circle of S 2 for n = 3. The problem is to determine f from 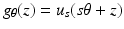 for some s with | s | > r and z ∈ θ ⊥ . The decisive tool for the error estimate is an estimate for the operator
for some s with | s | > r and z ∈ θ ⊥ . The decisive tool for the error estimate is an estimate for the operator
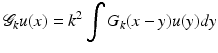 in L 2( | x | < r). In [41] it has been shown that
in L 2( | x | < r). In [41] it has been shown that
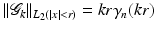 where γ n is a function with
where γ n is a function with 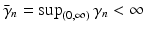 . For instance,
. For instance, 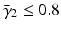 . We have
. We have 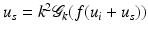 , hence, with
, hence, with 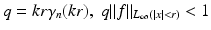
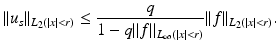
We introduce the propagation operator
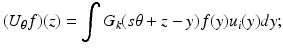 see [14]. For the (n − 1)-dimensional Fourier transform of U θ in θ ⊥ , we have
see [14]. For the (n − 1)-dimensional Fourier transform of U θ in θ ⊥ , we have
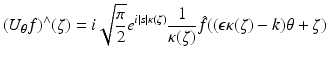 where
where 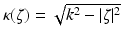 and ε = sgn(s). This is essentially Theorem 3.1 of [50].
and ε = sgn(s). This is essentially Theorem 3.1 of [50].
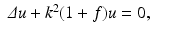
(11)
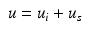
(12)
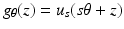 for some s with | s | > r and z ∈ θ ⊥ . The decisive tool for the error estimate is an estimate for the operator
for some s with | s | > r and z ∈ θ ⊥ . The decisive tool for the error estimate is an estimate for the operator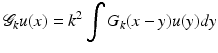
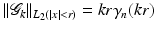
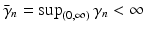 . For instance,
. For instance, 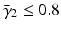 . We have
. We have 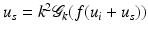 , hence, with
, hence, with 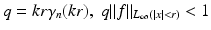
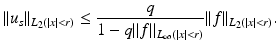
(13)
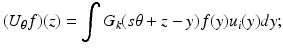
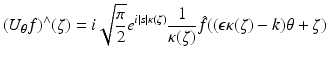
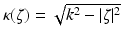 and ε = sgn(s). This is essentially Theorem 3.1 of [50].
and ε = sgn(s). This is essentially Theorem 3.1 of [50].We have
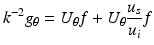 hence
hence
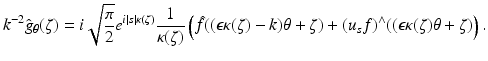 Now let ξ ∈ R n be in the ball | ξ | < 2k. We can find θ ∈ S n−1, ζ ∈ θ ⊥ with
Now let ξ ∈ R n be in the ball | ξ | < 2k. We can find θ ∈ S n−1, ζ ∈ θ ⊥ with 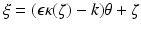 . For any such choice of θ and ζ, the last formula yields
. For any such choice of θ and ζ, the last formula yields
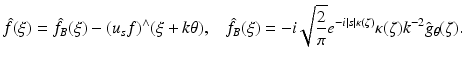 Since
Since
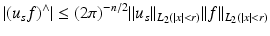 we have for | ξ | ≤ 2k
we have for | ξ | ≤ 2k
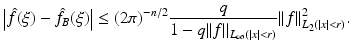
Thus we obtained an approximation of second order in f for 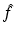 in the ball | ξ | ≤ 2k. This is what we expect from the Born approximation. The restriction to the bandwidth 2k is also natural as this corresponds to the maximal spatial resolution of π∕k.
in the ball | ξ | ≤ 2k. This is what we expect from the Born approximation. The restriction to the bandwidth 2k is also natural as this corresponds to the maximal spatial resolution of π∕k.
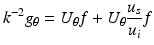
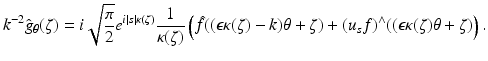
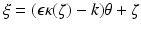 . For any such choice of θ and ζ, the last formula yields
. For any such choice of θ and ζ, the last formula yields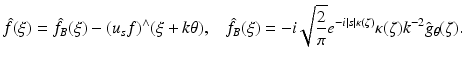
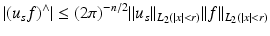
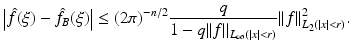
(14)
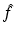 in the ball | ξ | ≤ 2k. This is what we expect from the Born approximation. The restriction to the bandwidth 2k is also natural as this corresponds to the maximal spatial resolution of π∕k.
in the ball | ξ | ≤ 2k. This is what we expect from the Born approximation. The restriction to the bandwidth 2k is also natural as this corresponds to the maximal spatial resolution of π∕k.We see from (14) that the decisive quantity for the Born approximation to be valid is 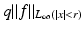 . In the engineering literature, see, e.g., [32], it is well known that this is a measure for the phase shift generated by the object f. Thus we arrive at the conclusion that the Born approximation works if the phase shift is sufficiently small. We also conclude from (14) that the reconstruction process, if restricted to the resolution π∕k is fairly stable: there are no unstable operations in the computation of
. In the engineering literature, see, e.g., [32], it is well known that this is a measure for the phase shift generated by the object f. Thus we arrive at the conclusion that the Born approximation works if the phase shift is sufficiently small. We also conclude from (14) that the reconstruction process, if restricted to the resolution π∕k is fairly stable: there are no unstable operations in the computation of 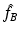 . It has been shown in [53] that this is also the case for the fully nonlinear problem, provided the geodesics behave reasonably. Thus the frequently discussed instability of the inverse scattering problem is just a consequence of an inadequate choice of the frequency of the irradiating waves.
. It has been shown in [53] that this is also the case for the fully nonlinear problem, provided the geodesics behave reasonably. Thus the frequently discussed instability of the inverse scattering problem is just a consequence of an inadequate choice of the frequency of the irradiating waves.
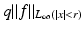 . In the engineering literature, see, e.g., [32], it is well known that this is a measure for the phase shift generated by the object f. Thus we arrive at the conclusion that the Born approximation works if the phase shift is sufficiently small. We also conclude from (14) that the reconstruction process, if restricted to the resolution π∕k is fairly stable: there are no unstable operations in the computation of
. In the engineering literature, see, e.g., [32], it is well known that this is a measure for the phase shift generated by the object f. Thus we arrive at the conclusion that the Born approximation works if the phase shift is sufficiently small. We also conclude from (14) that the reconstruction process, if restricted to the resolution π∕k is fairly stable: there are no unstable operations in the computation of 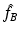 . It has been shown in [53] that this is also the case for the fully nonlinear problem, provided the geodesics behave reasonably. Thus the frequently discussed instability of the inverse scattering problem is just a consequence of an inadequate choice of the frequency of the irradiating waves.
. It has been shown in [53] that this is also the case for the fully nonlinear problem, provided the geodesics behave reasonably. Thus the frequently discussed instability of the inverse scattering problem is just a consequence of an inadequate choice of the frequency of the irradiating waves. 4 The Nonlinear Problem in the Time Domain
In this section we deal with the problem in the form (1)–(3). We suggest a very simple but practically useful iterative method and discuss some theoretical and practical aspects of it.
The Kaczmarz Method in the Time Domain
For a finite number of sources 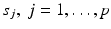 we have to solve a system of the form
we have to solve a system of the form
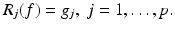
where R j is an operator between a Hilbert space H of functions on Ω × (0, T) and certain Hilbert spaces H j of functions on Γ × (0, T). In our case the operator R j is defined by R j (f) = u j | Γ×(0, T), where u j is the solution of (1)–(3) for the source s = s j .
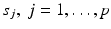 we have to solve a system of the form
we have to solve a system of the form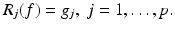
(15)
A natural method for solving (15) is the Kaczmarz method. This is an iterative method with the update
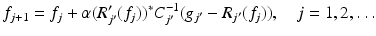 where j ′ = j mod p. Here, R j ′ is the Fréchet derivative of R j , R j ′ ∗ its adjoint, and C j is a positive definite operator. Going through all the equations once is called a complete sweep of the Kaczmarz method.
where j ′ = j mod p. Here, R j ′ is the Fréchet derivative of R j , R j ′ ∗ its adjoint, and C j is a positive definite operator. Going through all the equations once is called a complete sweep of the Kaczmarz method.
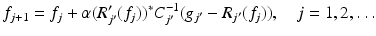
In the linear case, i.e., if R j : H → H j is a linear bounded operator the convergence of the Kaczmarz method is well understood, in particular for the case of CT; see, e.g., [50], Theorem 5.1.
If C j − R j R j ∗ is positive semidefinite, the sequence f j converges for 0 < α < 2 to 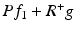 , where P is the orthogonal projection on the nullspace of
, where P is the orthogonal projection on the nullspace of 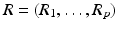 and R + is the Moore–Penrose generalized inverse of R. In the nonlinear case the situation is much less clear, see [6] for a theoretical discussion of the issue.
and R + is the Moore–Penrose generalized inverse of R. In the nonlinear case the situation is much less clear, see [6] for a theoretical discussion of the issue.
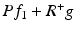 , where P is the orthogonal projection on the nullspace of
, where P is the orthogonal projection on the nullspace of 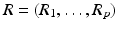 and R + is the Moore–Penrose generalized inverse of R. In the nonlinear case the situation is much less clear, see [6] for a theoretical discussion of the issue.
and R + is the Moore–Penrose generalized inverse of R. In the nonlinear case the situation is much less clear, see [6] for a theoretical discussion of the issue.The Kaczmarz method is not to be confused with the Landweber iteration. In the Landweber method one does the update only after all the equations have been processed, while in Kaczmarz we do the update as soon as a single equation is processed. In practice Kaczmarz turns out to be much faster than Landweber. In the linear finite dimensional case Kaczmarz is identical to the SOR method, see Theorem 5.2 in [50]. Also, the speed of convergence depends on the ordering of the sources. Sequential ordering does not yield the best results. Sophisticated arrangements, in particular random orderings, are much better. For the case of CT, see Section 5.3.1 of [50].
In order to compute R j ′ (f) for our imaging problem, we replace f by f + h and u j by u j + w with h, w small and ignore higher order terms. We get for w the differential equation
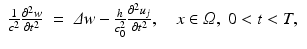
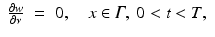
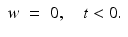
Hence we expect that
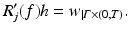 In fact it has been shown in [16] that with a suitable choice of Hilbert spaces H, H j the operator R j is Fréchet differentiable and the expression above is the derivative. A possible choice is H = H 2(Ω), restricted to functions f > −1, and
In fact it has been shown in [16] that with a suitable choice of Hilbert spaces H, H j the operator R j is Fréchet differentiable and the expression above is the derivative. A possible choice is H = H 2(Ω), restricted to functions f > −1, and 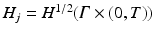 .
.
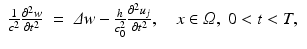
(16)
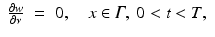
(17)
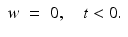
(18)
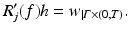
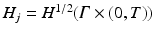 .
.Now we come to the problem of computing the adjoint of R j ′ . For this we have to specify the spaces H, H j . To make things easy, we put 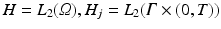 , i.e., we consider R j ′ as an unbounded operator between these spaces. Then the adjoint R j ′ ∗ satisfies
, i.e., we consider R j ′ as an unbounded operator between these spaces. Then the adjoint R j ′ ∗ satisfies
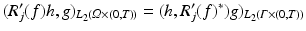 for sufficiently smooth functions h, g. Determining the exact domain of definition of the adjoint is a more tricky question which is not considered here.
for sufficiently smooth functions h, g. Determining the exact domain of definition of the adjoint is a more tricky question which is not considered here.
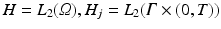 , i.e., we consider R j ′ as an unbounded operator between these spaces. Then the adjoint R j ′ ∗ satisfies
, i.e., we consider R j ′ as an unbounded operator between these spaces. Then the adjoint R j ′ ∗ satisfies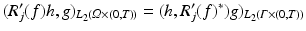
To find an explicit form of the adjoint, we follow [38]. We start out from the identity
![$$\displaystyle\begin{array}{rcl} & & \int _{\varOmega }\int _{0}^{T}\left ( \frac{1} {c^{2}} \frac{\partial ^{2}w} {\partial t^{2}} -\varDelta w\right )zdtdx -\int _{\varOmega }\int _{0}^{T}\left ( \frac{1} {c^{2}} \frac{\partial ^{2}z} {\partial t^{2}} -\varDelta z\right )wdtdx {}\\ & & =\int _{\varGamma }\int _{0}^{T}\left (\frac{\partial z} {\partial \nu } w - z\frac{\partial w} {\partial \nu } \right )dtdx + \left [\int _{\varOmega } \frac{1} {c^{2}}\left (\frac{\partial w} {\partial t} z - w\frac{\partial z} {\partial t}\right )dx\right ]_{0}^{T}. {}\\ \end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_37_Chapter_Equ22.gif) where ν is the exterior normal on Γ. This holds for any sufficiently smooth functions w, z on Ω × (0, T). Choosing for w the solution of (16)–(18) with u = u j the solution of (1)–(3) for source j and for z the solution of the final value problem
where ν is the exterior normal on Γ. This holds for any sufficiently smooth functions w, z on Ω × (0, T). Choosing for w the solution of (16)–(18) with u = u j the solution of (1)–(3) for source j and for z the solution of the final value problem
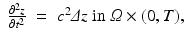




![$$\displaystyle\begin{array}{rcl} & & \int _{\varOmega }\int _{0}^{T}\left ( \frac{1} {c^{2}} \frac{\partial ^{2}w} {\partial t^{2}} -\varDelta w\right )zdtdx -\int _{\varOmega }\int _{0}^{T}\left ( \frac{1} {c^{2}} \frac{\partial ^{2}z} {\partial t^{2}} -\varDelta z\right )wdtdx {}\\ & & =\int _{\varGamma }\int _{0}^{T}\left (\frac{\partial z} {\partial \nu } w - z\frac{\partial w} {\partial \nu } \right )dtdx + \left [\int _{\varOmega } \frac{1} {c^{2}}\left (\frac{\partial w} {\partial t} z - w\frac{\partial z} {\partial t}\right )dx\right ]_{0}^{T}. {}\\ \end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_37_Chapter_Equ22.gif)
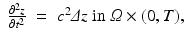
(19)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree