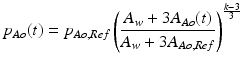Fig. 1.
CircAdapt model representation (left) with aorta and aortic valve parameters (right). RA: right atrium, LA: left atrium, RV: right ventricle, LV: left ventricle, TV: tricuspid valve, PV: pulmonary valve, MV: mitral valve, pAo: aortic pressure, AAo: cross-sectional area of the aorta, Aw: cross-sectional area of the aortic wall, ALV: cross-sectional area of the left ventricle, pLV: left ventricular pressure, AAoValve: cross-sectional area of the aortic valve, lAoValve: length of the aortic valve, Δp: pressure drop across the aortic valve.
2.2 Aortic Valve
The aortic valve is modeled as described previously [6], and can be used for healthy and pathological valve functions. The aortic valve is a narrow and varying orifice area where blood flow, 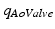 , passes through assuming unsteady, incompressible and non-viscous plug flow. Blood flow is considered forward flow (
, passes through assuming unsteady, incompressible and non-viscous plug flow. Blood flow is considered forward flow (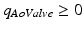 ) when it travels from the LV into the aorta, and backward flow (
) when it travels from the LV into the aorta, and backward flow (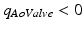 ) in the opposite direction. The aortic valve mechanics is governed by the differential equation:
) in the opposite direction. The aortic valve mechanics is governed by the differential equation:
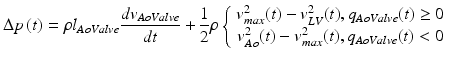
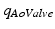 , passes through assuming unsteady, incompressible and non-viscous plug flow. Blood flow is considered forward flow (
, passes through assuming unsteady, incompressible and non-viscous plug flow. Blood flow is considered forward flow (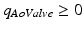 ) when it travels from the LV into the aorta, and backward flow (
) when it travels from the LV into the aorta, and backward flow (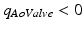 ) in the opposite direction. The aortic valve mechanics is governed by the differential equation:
) in the opposite direction. The aortic valve mechanics is governed by the differential equation: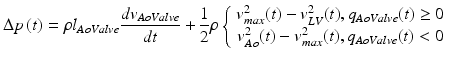
(1)
The blood flow across the valve at time 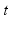 ,
, 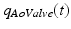 , causes a transvalvular pressure drop,
, causes a transvalvular pressure drop, 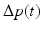 , which is the sum of inertia and Bernoulli effects (first and second right hand terms in Eq. 1, respectively). Briefly, the inertia term in Eq. 1 adds the effect of blood acceleration in change of pressure between the LV and the aorta by considering the valve as a small channel (with length
, which is the sum of inertia and Bernoulli effects (first and second right hand terms in Eq. 1, respectively). Briefly, the inertia term in Eq. 1 adds the effect of blood acceleration in change of pressure between the LV and the aorta by considering the valve as a small channel (with length 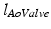 ) where blood flow has a velocity change in time
) where blood flow has a velocity change in time 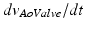 . The second right hand term adds the kinetic energy that must be conserved along a streamline of flow according to Bernoulli’s law (neglecting gravitation and pressure loss due to friction or turbulence). Flow velocities at the aortic valve, at the LV and at the aorta are
. The second right hand term adds the kinetic energy that must be conserved along a streamline of flow according to Bernoulli’s law (neglecting gravitation and pressure loss due to friction or turbulence). Flow velocities at the aortic valve, at the LV and at the aorta are 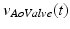 ,
, 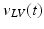 and
and 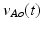 , respectively, and
, respectively, and 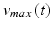 is:
is:
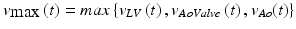
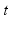 ,
, 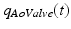 , causes a transvalvular pressure drop,
, causes a transvalvular pressure drop, 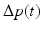 , which is the sum of inertia and Bernoulli effects (first and second right hand terms in Eq. 1, respectively). Briefly, the inertia term in Eq. 1 adds the effect of blood acceleration in change of pressure between the LV and the aorta by considering the valve as a small channel (with length
, which is the sum of inertia and Bernoulli effects (first and second right hand terms in Eq. 1, respectively). Briefly, the inertia term in Eq. 1 adds the effect of blood acceleration in change of pressure between the LV and the aorta by considering the valve as a small channel (with length 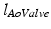 ) where blood flow has a velocity change in time
) where blood flow has a velocity change in time 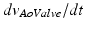 . The second right hand term adds the kinetic energy that must be conserved along a streamline of flow according to Bernoulli’s law (neglecting gravitation and pressure loss due to friction or turbulence). Flow velocities at the aortic valve, at the LV and at the aorta are
. The second right hand term adds the kinetic energy that must be conserved along a streamline of flow according to Bernoulli’s law (neglecting gravitation and pressure loss due to friction or turbulence). Flow velocities at the aortic valve, at the LV and at the aorta are 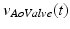 ,
, 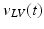 and
and 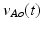 , respectively, and
, respectively, and 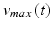 is:
is: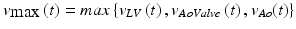
(2)
All flow velocities are computed as the flow passing across the aortic valve 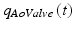 divided by the corresponding cross-sectional area at
divided by the corresponding cross-sectional area at 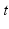 . Blood density is
. Blood density is 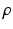 . The orifice area of the aortic valve at instant
. The orifice area of the aortic valve at instant 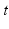 ,
, 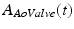 , is defined by an opening orifice area (OOA) and a regurgitant orifice area (ROA), which corresponds to the cross-sectional area of the opened and closed (or regurgitant) valve, respectively. The signs of pressure drop
, is defined by an opening orifice area (OOA) and a regurgitant orifice area (ROA), which corresponds to the cross-sectional area of the opened and closed (or regurgitant) valve, respectively. The signs of pressure drop 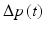 and blood flow
and blood flow 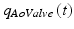 determine whether the valve is opened or closed at
determine whether the valve is opened or closed at 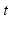 . Therefore, an ROA value greater than 0 allows simulating AR. In the healthy situation, the OOA and ROA of the aortic valve are 5 cm2 and 0 cm2, respectively.
. Therefore, an ROA value greater than 0 allows simulating AR. In the healthy situation, the OOA and ROA of the aortic valve are 5 cm2 and 0 cm2, respectively.
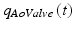 divided by the corresponding cross-sectional area at
divided by the corresponding cross-sectional area at 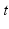 . Blood density is
. Blood density is 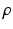 . The orifice area of the aortic valve at instant
. The orifice area of the aortic valve at instant 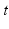 ,
, 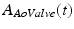 , is defined by an opening orifice area (OOA) and a regurgitant orifice area (ROA), which corresponds to the cross-sectional area of the opened and closed (or regurgitant) valve, respectively. The signs of pressure drop
, is defined by an opening orifice area (OOA) and a regurgitant orifice area (ROA), which corresponds to the cross-sectional area of the opened and closed (or regurgitant) valve, respectively. The signs of pressure drop 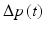 and blood flow
and blood flow 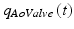 determine whether the valve is opened or closed at
determine whether the valve is opened or closed at 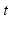 . Therefore, an ROA value greater than 0 allows simulating AR. In the healthy situation, the OOA and ROA of the aortic valve are 5 cm2 and 0 cm2, respectively.
. Therefore, an ROA value greater than 0 allows simulating AR. In the healthy situation, the OOA and ROA of the aortic valve are 5 cm2 and 0 cm2, respectively.2.3 Aortic Compliance
The aorta is modeled as a compliant large blood vessel, whose proximal element is the aortic valve and whose distal element is the systemic circulation resistance. The vessel hemodynamics are governed by a pressure-cross-sectional area relationship arising from stress and strain in the vessel walls [6] (see Eq. 3). 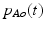 and
and 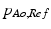 are the current and the reference transmural pressure of the aorta, respectively; and
are the current and the reference transmural pressure of the aorta, respectively; and 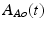 and
and 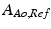 are the current and the reference cross-sectional area of the aorta, respectively.
are the current and the reference cross-sectional area of the aorta, respectively. 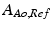 is defined as the cross-sectional area such that the aortic pressure is the reference transmural pressure
is defined as the cross-sectional area such that the aortic pressure is the reference transmural pressure 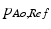 .
. 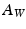 is the cross-sectional area of the aortic wall.
is the cross-sectional area of the aortic wall.
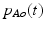 and
and 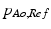 are the current and the reference transmural pressure of the aorta, respectively; and
are the current and the reference transmural pressure of the aorta, respectively; and 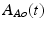 and
and 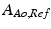 are the current and the reference cross-sectional area of the aorta, respectively.
are the current and the reference cross-sectional area of the aorta, respectively. 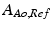 is defined as the cross-sectional area such that the aortic pressure is the reference transmural pressure
is defined as the cross-sectional area such that the aortic pressure is the reference transmural pressure 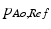 .
. 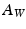 is the cross-sectional area of the aortic wall.
is the cross-sectional area of the aortic wall.