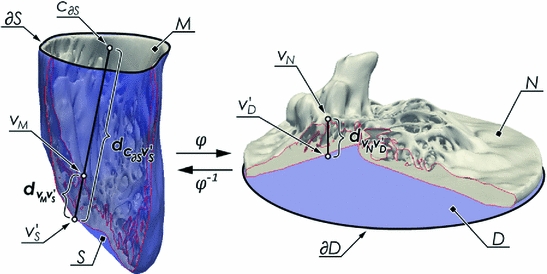
to different subject meshes M, we are locating two anatomical landmark points on their corresponding base meshes S. As cardiac landmarks we use the apex and the mid-septal point of the mitral annulus  . The mid-septal point of
. The mid-septal point of 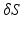 is manually defined by the user, while the apex is defined as the furthest point from the centroid
is manually defined by the user, while the apex is defined as the furthest point from the centroid 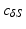 of
of 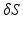 .
.
2.1 Mapping of the Anatomical Base Mesh to a Planar Domain
As the planar domain for S we used a unit disk following the approach of De Craene et al. [16]. As implied by the Riemann Mapping Theorem, any surface homeomorphic to a disk can be conformally mapped into any simply-connected region of the plane. The only requirement is that our mapping is harmonic, meaning that every surface coordinate has to have a vanishing Laplacian. Therefore we are computing a bijective mapping 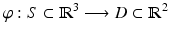 , where S is the anatomical base surface mesh of the LV and D is a unit disk. The boundary
, where S is the anatomical base surface mesh of the LV and D is a unit disk. The boundary 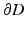 of D is defined by uniformly sampling a unit circle with the number of samples equal to the number of points on the boundary
of D is defined by uniformly sampling a unit circle with the number of samples equal to the number of points on the boundary 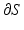 and the following system of linear equations is solved for the coordinates of the points inside the disk:
and the following system of linear equations is solved for the coordinates of the points inside the disk:
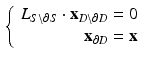
The boundary x, y coordinates are given by the columns of matrix 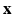 .
. 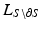 represents the Laplacian matrix of the mesh S with the rows corresponding to its boundary
represents the Laplacian matrix of the mesh S with the rows corresponding to its boundary 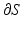 removed.
removed. 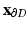 and
and 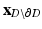 are the matrices of coordinates of the points on the disk (the one we are calculating and that define our mapping) corresponding to the boundary and the interior, respectively. The desired mapping is then given by (1), while the connectivity information is retained from the mesh S. An example of the mapping can be seen in Fig. 1.
are the matrices of coordinates of the points on the disk (the one we are calculating and that define our mapping) corresponding to the boundary and the interior, respectively. The desired mapping is then given by (1), while the connectivity information is retained from the mesh S. An example of the mapping can be seen in Fig. 1.
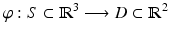 , where S is the anatomical base surface mesh of the LV and D is a unit disk. The boundary
, where S is the anatomical base surface mesh of the LV and D is a unit disk. The boundary 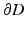 of D is defined by uniformly sampling a unit circle with the number of samples equal to the number of points on the boundary
of D is defined by uniformly sampling a unit circle with the number of samples equal to the number of points on the boundary 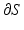 and the following system of linear equations is solved for the coordinates of the points inside the disk:
and the following system of linear equations is solved for the coordinates of the points inside the disk: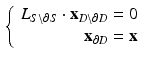
(1)
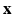 .
. 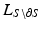 represents the Laplacian matrix of the mesh S with the rows corresponding to its boundary
represents the Laplacian matrix of the mesh S with the rows corresponding to its boundary 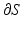 removed.
removed. 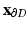 and
and 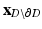 are the matrices of coordinates of the points on the disk (the one we are calculating and that define our mapping) corresponding to the boundary and the interior, respectively. The desired mapping is then given by (1), while the connectivity information is retained from the mesh S. An example of the mapping can be seen in Fig. 1.
are the matrices of coordinates of the points on the disk (the one we are calculating and that define our mapping) corresponding to the boundary and the interior, respectively. The desired mapping is then given by (1), while the connectivity information is retained from the mesh S. An example of the mapping can be seen in Fig. 1.As a result of this mapping, the position of the apex in the planar domain will still be variable and depend on the specific anatomy. However in order to define a subject independent frame we must make sure that the apex is consistently mapped to the same point which is achieved using thin plate splines, mapping the boundary to itself and the apex to the center of the disk. This additional step will enforce a more consistent localization of the cardiac regions among different subjects, but reduce the conformal map to quasi-conformal.
2.2 Elimination of Orientation Ambiguity
To assure correspondence of parametrized meshes N and D between subjects we are removing orientation ambiguity by assigning the same coordinate values to their mid-septal landmarks. Thus during the mapping to a unit disk we are placing these landmarks at the same location 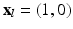 (l is the index of the landmark in the array of all the points).
(l is the index of the landmark in the array of all the points).
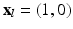 (l is the index of the landmark in the array of all the points).
(l is the index of the landmark in the array of all the points).2.3 Mapping the Detailed LV Anatomy
Once we have the outer surface S of the LV mapped to the disk D, we have provided a base of a subject independent reference frame on top of which we want to map a detailed mesh M. To do so, we first project the vertices of M onto S. The common way of achieving this would be to locate the closest point 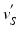 for every vertex
for every vertex 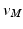 . As the LV has structures traversing thorough the whole cavity, the closest point projection will not project the neighbourhoods of
. As the LV has structures traversing thorough the whole cavity, the closest point projection will not project the neighbourhoods of 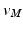 ’s to the neighbourhoods of
’s to the neighbourhoods of 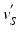 ’s. Such projection will cause the mapping function
’s. Such projection will cause the mapping function 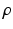 to be non-bijective and result in a highly distorted mesh N.
to be non-bijective and result in a highly distorted mesh N.
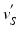 for every vertex
for every vertex 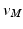 . As the LV has structures traversing thorough the whole cavity, the closest point projection will not project the neighbourhoods of
. As the LV has structures traversing thorough the whole cavity, the closest point projection will not project the neighbourhoods of 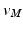 ’s to the neighbourhoods of
’s to the neighbourhoods of 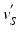 ’s. Such projection will cause the mapping function
’s. Such projection will cause the mapping function 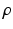 to be non-bijective and result in a highly distorted mesh N.
to be non-bijective and result in a highly distorted mesh N.To alleviate the above problem, we project the points by casting rays through all vertices 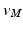 from a fixed point
from a fixed point 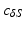 and locate the corresponding intersection points
and locate the corresponding intersection points 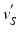 . As the fixed point
. As the fixed point 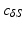 , we take a centroid of the surface boundary
, we take a centroid of the surface boundary 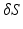 . The choice of the centroid of the mitral annulus as the origin of the rays is motivated by the fact that its location is free of any detailed structures we want to parametrize.
. The choice of the centroid of the mitral annulus as the origin of the rays is motivated by the fact that its location is free of any detailed structures we want to parametrize.
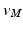 from a fixed point
from a fixed point 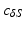 and locate the corresponding intersection points
and locate the corresponding intersection points 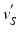 . As the fixed point
. As the fixed point 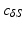 , we take a centroid of the surface boundary
, we take a centroid of the surface boundary 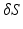 . The choice of the centroid of the mitral annulus as the origin of the rays is motivated by the fact that its location is free of any detailed structures we want to parametrize.
. The choice of the centroid of the mitral annulus as the origin of the rays is motivated by the fact that its location is free of any detailed structures we want to parametrize.Subsequently, 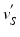 points are mapped to
points are mapped to 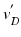 points using the map calculated in Subsect. 2.1. Finally, for every
points using the map calculated in Subsect. 2.1. Finally, for every 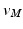 , we calculate its distance
, we calculate its distance 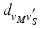 along the ray to the corresponding
along the ray to the corresponding 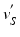 normalized by the length
normalized by the length 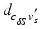 of the ray segment between
of the ray segment between 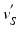 and
and 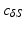 . Then the vertices
. Then the vertices 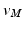 are mapped to our reference frame by placing them along the normal direction of
are mapped to our reference frame by placing them along the normal direction of 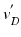 at the distance
at the distance 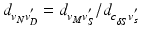 . The transformed vertices
. The transformed vertices 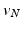 of N have the same connectivity as
of N have the same connectivity as 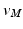 of M.
of M.
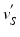 points are mapped to
points are mapped to 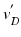 points using the map calculated in Subsect. 2.1. Finally, for every
points using the map calculated in Subsect. 2.1. Finally, for every 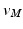 , we calculate its distance
, we calculate its distance 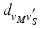 along the ray to the corresponding
along the ray to the corresponding 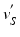 normalized by the length
normalized by the length 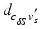 of the ray segment between
of the ray segment between 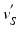 and
and 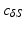 . Then the vertices
. Then the vertices 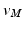 are mapped to our reference frame by placing them along the normal direction of
are mapped to our reference frame by placing them along the normal direction of 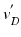 at the distance
at the distance 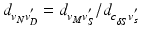 . The transformed vertices
. The transformed vertices 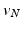 of N have the same connectivity as
of N have the same connectivity as 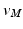 of M.
of M.