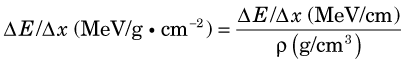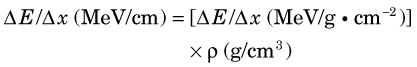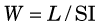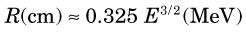chapter 6 Interaction of Radiation with Matter
The two most important general types of radiation emitted during radioactive decay are charged particles, such as α particles and β particles, and electromagnetic radiation (photons), such as γ rays and x rays. These radiations transfer their energy to matter as they pass through it. The principle mechanisms for energy transfer are ionization and excitation of atoms and molecules. Most of this energy ultimately is degraded into heat (atomic and molecular vibrations); however, the ionization effect has other important consequences. For this reason, the radiations emitted during radioactive decay often are called ionizing radiations. The processes by which ionizing radiations transfer their energy to matter are fundamental to the detection of radiation, discussed in Chapter 7. As well, they are important for radiation dosimetry, discussed in Chapter 22. In this chapter, we discuss those processes in some detail. Because the mechanisms differ, they are discussed separately for particulate versus electromagnetic radiation.
a Interactions of Charged Particles with Matter
1 Charged-Particle Interaction Mechanisms
High-energy charged particles, such as α particles or β particles, lose energy and slow down as they pass through matter, as a result of collisions with atoms and molecules. High-energy electrons, which also are charged particles, are a byproduct of these collisions. In addition, high-energy electrons are generated when γ rays and x rays interact with matter, and they are emitted in internal conversion (see Chapter 3, Section E) and in the Auger effect (see Chapter 2, Section C.3).
For these reasons, this section emphasizes the interactions of electrons with matter. Except for differences in sign, the forces experienced by positive and negative electrons (e.g., β+ and β− particles) are identical. There are minor differences between the ionizing interactions of these two types of particles, but they are not of importance to nuclear medicine and are not discussed here. In this chapter, the term electrons is meant to include both the positive and negative types. The annihilation effect, which occurs when a positive electron (positron) has lost all of its kinetic energy and stopped, is discussed in Chapter 3, Section G.
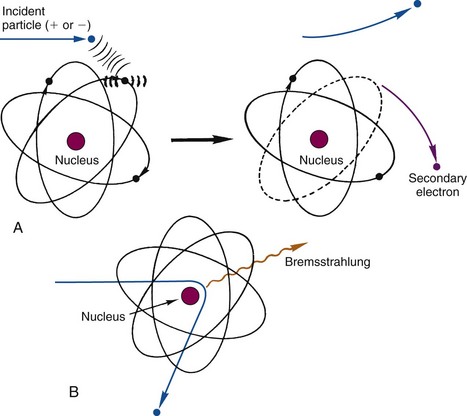
The “collisions” that occur between a charged particle and atoms or molecules involve electrical forces of attraction or repulsion rather than actual mechanical contact. For example, a charged particle passing near an atom exerts electrical forces on the orbital electrons of that atom. In a close encounter, the strength of the forces may be sufficient to cause an orbital electron to be separated from the atom, thus causing ionization (Fig. 6-1A). An ionization interaction looks like a collision between the charged particle and an orbital electron. The charged particle loses energy in the collision. Part of this energy is used to overcome the binding energy of the electron to the atom, and the remainder is given to the ejected secondary electron as kinetic energy. Ionization involving an inner-shell electron eventually leads to the emission of characteristic x rays or Auger electrons; however, these effects generally are very small, because most ionization interactions involve outer-shell electrons. The ejected electron may be sufficiently energetic to cause secondary ionizations on its own. Such an electron is called a delta (δ) ray.
A less-close encounter between a charged particle and an atom may result in an orbital electron being raised to an excited state, thus causing atomic or molecular excitation. These interactions generally result in smaller energy losses than occur in ionization events. The energy transferred to an atom in an excitation interaction is dissipated in molecular vibrations, atomic emission of infrared, visible, ultraviolet radiation, and so forth.
A third type of interaction occurs when the charged particle actually penetrates the orbital electron cloud of an atom and interacts with its nucleus. For a heavy charged particle of sufficiently high energy, such as an α particle or a proton, this may result in nuclear reactions of the types used for the production of radionuclides (see Chapter 5); however, for both heavy charged particles and electrons, a more likely result is that that particle will simply be deflected by the strong electrical forces exerted on it by the nucleus (Fig. 6-1B). The particle is rapidly decelerated and loses energy in the “collision.” The energy appears as a photon of electromagnetic radiation, called bremsstrahlung (German for “braking radiation”).
The energy of bremsstrahlung photons can range anywhere from nearly zero (events in which the particle is only slightly deflected) up to a maximum equal to the full energy of the incident particle (events in which the particle is virtually stopped in the collision). Figure 6-2 shows the energy spectrum for bremsstrahlung photons generated in aluminum by particles from a 90Sr-90Y source mixture (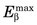 = 2.27 MeV) and illustrates that most of the photons are in the lower energy range.
= 2.27 MeV) and illustrates that most of the photons are in the lower energy range.
2 Collisional Versus Radiation Losses
Energy losses incurred by a charged particle in ionization and excitation events are called collisional losses, whereas those incurred in nuclear encounters, resulting in bremsstrahlung production, are called radiation losses. In the nuclear medicine energy range, collisional losses are by far the dominating factor (See Fig. 6-5). Radiation losses increase with increasing particle energy and with increasing atomic number of the absorbing medium. An approximation for percentage radiation losses for β particles having maximum energy 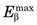 (MeV) is
(MeV) is
where Z is the atomic number of the absorber. This approximation is accurate to within approximately 30%. For a mixture of elements, an “effective” atomic number for bremsstrahlung production should be used
where f1, f2, … are the fractions by weight of the elements Z1, Z2, … in the mixture.
Answer
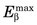 = 1.7 MeV for 32P. Water comprises
= 1.7 MeV for 32P. Water comprises  parts hydrogen (Z = 1, AW ≈ 1) and
parts hydrogen (Z = 1, AW ≈ 1) and 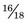 parts oxygen (Z = 8, AW ≈ 16); thus its effective atomic number for bremsstrahlung production is (Equation 6-2)
parts oxygen (Z = 8, AW ≈ 16); thus its effective atomic number for bremsstrahlung production is (Equation 6-2)
The percentage of radiation losses in water are therefore (Equation 6-1)
The remaining 99.6% and 95.4%, respectively, are dissipated as collisional losses.
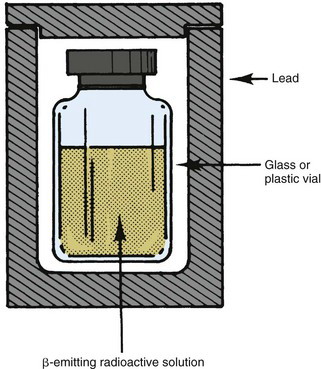
Example 6-1 demonstrates that high-energy electrons in the nuclear medicine energy range dissipate most of their energy in collisional losses. Bremsstrahlung production accounts for only a small fraction of their energy. Nevertheless, bremsstrahlung can be important in some situations, such as the shielding of relatively large quantities of an energetic β-particle emitter (e.g., hundreds of MBq of 32P). The β particles themselves are easily stopped by only a few millimeters of plastic, glass, or lead (see Section B.2); however, the bremsstrahlung photons they generate are much more penetrating and may require additional shielding around the primary β-particle shielding. It is helpful in such situations to use a low-Z material, such as plastic, for the primary β-particle shielding, and then to surround this with a higher-Z material, such as lead, for bremsstrahlung shielding (Fig. 6-3). This arrangement minimizes bremsstrahlung production by the β particles in the shielding material.
Bremsstrahlung production and radiation losses for α particles and other heavy charged particles are very small because the amount of bremsstrahlung production is inversely proportional to the mass of the incident charged particle. Alpha particles and protons are thousands of times heavier than electrons and therefore dissipate only a few hundredths of 1% or less of their energy as radiation losses. These particles, even at energies up to 100 MeV, dissipate nearly all of their energy as collisional losses.
3 Charged-Particle Tracks
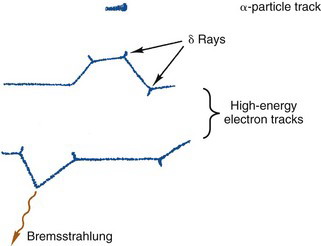
A charged particle passing through matter leaves a track of secondary electrons and ionized atoms in its path. In soft tissue and materials of similar density, the tracks are typically approximately 100 µm wide, with occasionally longer side tracks generated by energetic δ rays. The tracks are studied in nuclear physics using film emulsions, cloud chambers,* and other devices.
To illustrate these differences, Figure 6-4 shows (in greatly enlarged detail) some possible tracks for β particles and for α particles in water. The actual track lengths are on the order of microns for α particles and fractions of a centimeter for β particles. This is discussed further in Section B.
4 Deposition of Energy Along a Charged-Particle Track
Figure 6-5 shows collisional and radiation energy loss rates for electrons in the energy range of 0.01-10 MeV in water and in lead. Energy loss rates Δ E /λ x are expressed in MeV/g · cm–2 to normalize for density effects
Thus for a given density ρ the energy loss rate in MeV/cm is given by
Collisional loss rates Δ E /Δxcoll decrease with increasing electron energy, reflecting the velocity effect mentioned in Section A.3. Also, Δ E/Δxcoll decreases with increasing atomic number of the absorbing medium because in atoms of higher atomic number, inner-shell electrons are “screened” from the incident electron by layers of outer-shell electrons, making interactions with inner-shell electrons less likely in these atoms. Gram for gram, lighter elements are better absorbers of electron energy than are heavier elements.
Radiation loss rates Δ E /Δ x rad increase with increasing electron energy and increasing atomic number of the absorber. This is discussed in Section A.2.
The average value of the linear energy transfer measured along a charged-particle track, 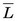 , is an important parameter in health physics (see Chapter 23, Section A.1.).
, is an important parameter in health physics (see Chapter 23, Section A.1.). 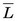 usually is expressed in units of keV/µm. For electrons in the energy range of 10 keV to 10 MeV traveling through soft tissue,
usually is expressed in units of keV/µm. For electrons in the energy range of 10 keV to 10 MeV traveling through soft tissue, 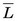 has values in the range of 0.2-2 keV/µm. Lower-energy electrons, for example, β particles emitted by 3H (
has values in the range of 0.2-2 keV/µm. Lower-energy electrons, for example, β particles emitted by 3H (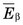 = 5.6 keV), have somewhat higher values of
= 5.6 keV), have somewhat higher values of 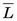 . Alpha particles have values of
. Alpha particles have values of 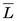 ≈ 100 keV/µm.
≈ 100 keV/µm.
This quantity has been measured and found to have a relatively narrow range of values in a variety of gases (25-45 eV per ion pair or, equivalently, per ionization) independent of the type or energy of the incident particle. The value for air is 33.7 eV per ion pair. W is not the same as the ionization potential (I), which is the average energy required to cause an ionization in a material (averaged over all the electron shells). Ionization potentials for gases are in the range 10-15 eV. The difference between W and I is energy dissipated by a charged particle in nonionizing excitation events. Apparently, more than half of the energy of a charged particle is expended in this way. Similar ratios between W and I are found in semiconductor solids, except that in these materials the values of W and I are both approximately a factor of 10 smaller than for gases (see Table 7-1).
Because W does not change appreciably with particle type or energy, specific ionization is proportional to linear energy transfer L along a charged particle track. Figure 6-6 shows specific ionization in air for electrons as a function of their energy. The curve indicates that specific ionization increases with decreasing energy down to an energy of approximately 100 eV. This behavior reflects the fact that energy loss rates and L increase as the electron slows down. Below approximately 100 eV, the electron energy is inadequate to cause ionizations efficiently, and specific ionization decreases rapidly to zero.
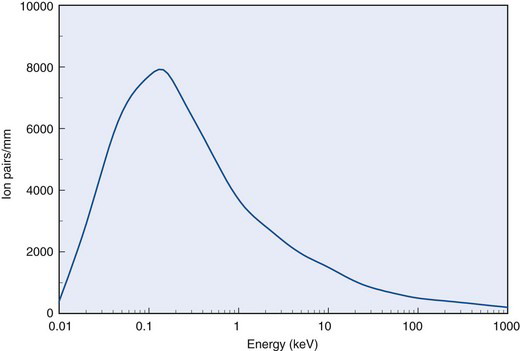
FIGURE 6-6 Specific ionization for electrons versus energy in water.
(Adapted from Mladjenovic M: Radioisotope and Radiation Physics. New York, 1973, Academic Press, p 145.)
Specific ionization values for α particles are typically 100 times greater than for electrons of the same energy because of their greater charge and much lower velocities. This leads to greater rates of energy loss, as discussed in previously in Section A.3.
The fact that specific ionization increases as a particle slows down leads to a marked increase in ionization density near the end of its track. This effect is especially pronounced for heavy particles. Figure 6-7 shows a graph of ionization density versus distance traveled for α particles in air. The peak near the end of the α-particle range is called the Bragg ionization peak.* A similar increase in ionization density is seen at the end of an electron track; however, the peak occurs when the electron energy has been reduced to less than approximately 1 keV, and it accounts for only a small fraction of its total energy.
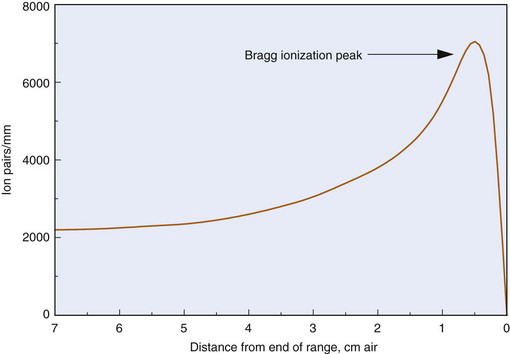
FIGURE 6-7 Specific ionization versus distance traveled for α particles in air.
(Adapted from Mladjenovic M: Radioisotope and Radiation Physics. New York, 1973, Academic Press, p 111.)
5 The Cerenkov Effect
An additional charged-particle interaction deserving brief mention is the Cerenkov (pronounced cher-en′-kof) effect. This effect occurs when a charged particle travels in a medium at a speed greater than the speed of light in that medium. The restriction that a particle cannot travel faster than the speed of light applies to the speed of light in a vacuum (c ≈ 3 × 108 m /sec); however, a 1-MeV β particle emitted in water travels with a velocity of v ≈ 0.8 c, whereas the speed of light in water (refractive index n = 1.33) is c′ = c/n ≈ 0.75 c. Under these conditions, the particle creates an electromagnetic “shock wave” in much the same way that an airplane traveling faster than the speed of sound creates an acoustic shock wave. The electromagnetic shock wave appears as a burst of visible radiation, typically bluish in color, called Cerenkov radiation. The Cerenkov effect can occur for electrons with energies of a few hundred keV; however, for heavy particles such as α particles and protons, energies of several thousands of MeV are required to meet the velocity requirements.
b Charged-Particle Ranges
1 Alpha Particles
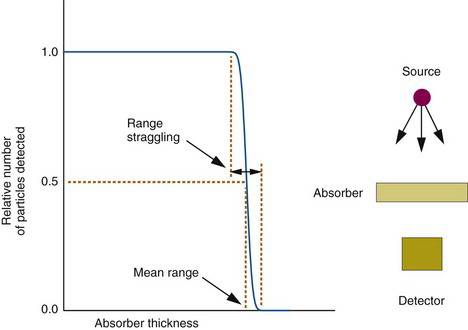
An α particle loses energy in a more or less continuous slowing-down process as it travels through matter. The particle is deflected only slightly in its collisions with atoms and orbital electrons. As a result, the distance traveled, or range, of an α particle depends only on its initial energy and on its average energy loss rate in the medium. For α particles of the same energy, the range is quite consistent from one particle to the next. A transmission curve, showing percent transmission for α particles versus thickness of absorber, remains essentially flat at 100% until the maximum range is reached; then it falls rapidly to zero (Fig. 6-8). The mean range is defined as the thickness resulting in 50% transmission. There is only a small amount of range fluctuation, or range straggling, about the mean value. Typically, range straggling amounts to only approximately 1% of the mean range.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


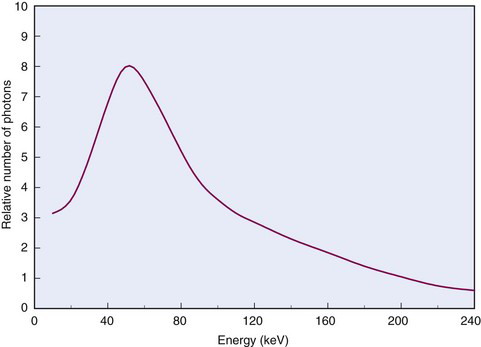
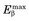 = 2.27 MeV) mixture in aluminum.
= 2.27 MeV) mixture in aluminum.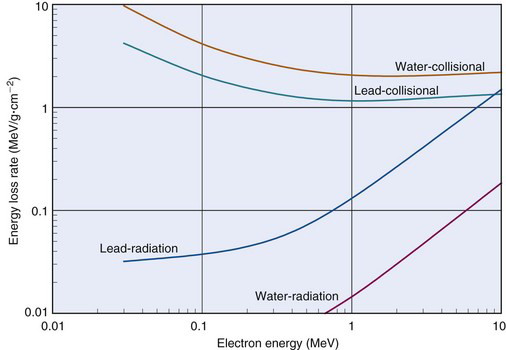
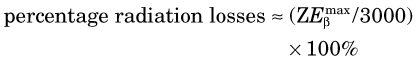
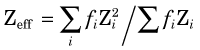
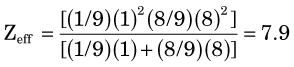
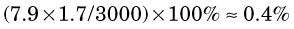
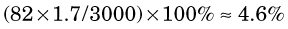
 10 MeV ), energy loss rates for charged particles increase linearly with the density of the absorbing medium. (At higher energies, density effects are more complicated, as discussed in the sources cited in the references and bibliography at the end of this chapter.)
10 MeV ), energy loss rates for charged particles increase linearly with the density of the absorbing medium. (At higher energies, density effects are more complicated, as discussed in the sources cited in the references and bibliography at the end of this chapter.)