Interaction of Radiation with Matter

Fig. 6.1

Illustration of Bragg ionization showing a peak near the end of the travel of the charged particle

Linear Energy Transfer

The linear energy transfer (LET) is the amount of energy deposited per unit length of the path by the radiation. From the preceding, it is clear that

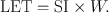
${\text{LET}} = {\text{SI}} \times W.$

(6.1)

The LET is expressed in units of keV/μm and is very useful in concepts of radiation protection. Electromagnetic radiations and β-particles interact with matter, losing only little energy per interaction and therefore have low LETs . In contrast, heavy particles (α-particles, neutrons, and protons) lose energy very rapidly, producing many ionizations in a short distance, and thus have high LETs. Some comparative approximate LET values in keV/mm in tissue are given in Table 6.1.

Table 6.1

LET values of some radiations in tissue

Radiation	LET (keV/μm)
3 MV x-rays	0.5
250 KV x-rays	3.0
5-MeV α-particles	100.0
1-MeV electrons	0.25
14-MeV neutrons	20.0

Problem 6.1

If a particulate radiation produces 45,000 ion pairs per centimeter in air, calculate the LET of the radiation.

Answer

W = 35 eV per ion pair

Using Eq. (6.1),

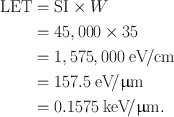
$\begin{aligned} {\text{LET}} & = {\text{SI}} \times W \\ & = 45,000 \times 35 \\ & = 1,575,000\;{\text{eV}}\!/{\text{cm}} \\ & = 157.5\;{\text{eV}}\!/\upmu{\text{m}} \\ & = 0.1575\;{\text{keV}}\!/\upmu {\text{m}}. \end{aligned}$

Range

The range (R) of a charged particle in an absorber is the straight-line distance traversed by the particle in the direction of the particle . The range of a particle depends on the mass, charge, and kinetic energy of the particle and also on the density of the absorber. The heavier and more highly charged particles have shorter ranges than lighter and lower charged particles. The range of charged particles increases with the energy of the particle. Thus, a 10-MeV particle will have a longer range than a 1-MeV particle. The range of the particle depends on the density of the absorber, in that the denser the absorber, the shorter the range. The unit of range is given in mg/cm² of the absorber.

Depending on the type of the charged particle, the entire path of travel may be unidirectional along the initial direction of motion, or tortuous (Fig. 6.2). Because the α-particle loses only a small fraction of energy in a single collision with an electron because of its heavier mass and is not appreciably deflected in the collision, the α-particle path is nearly a straight line along its initial direction (Fig. 6.2a). Many collisions in a short distance create many ion pairs in a small volume. In contrast, β-particles or electrons interact with extra nuclear orbital electrons of the same mass and are deflected considerably. This leads to tortuous paths of these particles (Fig. 6.2b). In this situation, the true range is less than the total path traveled by the particle.

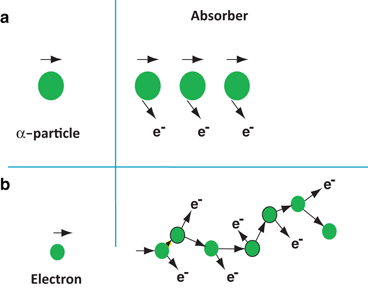
Fig. 6.2

Concept of passage of α particles and electrons through an absorber: a heavy α particles move in almost a straight line, b light electrons move in zigzag paths

It is seen that the ranges of all identical particles in a given absorber are not exactly the same but show a spread of 3–4 % near the end of their path (Fig. 6.3). This phenomenon, referred to as the straggling of the ranges , results from the statistical fluctuations in the number of collisions and in the energy loss per collision. The range straggling is less prominent with α-particles but is severe with electrons because it is mostly related to the mass of the particle. The light mass electrons are considerably deflected during collisions and hence exhibit more straggling. If the transmission of a beam of charged particles through absorbers of different thicknesses is measured, the beam intensity will remain constant until the region of range straggling is encountered, where the beam intensity falls sharply from its initial value to zero. The absorber thickness that reduces the beam intensity by one half is called the mean range . The mean range of heavier particles such as α-particles is more well defined than that of electrons. Because β ⁻-particles are emitted with a continuous energy spectrum, their absorption, and hence their ranges, become quite complicated.

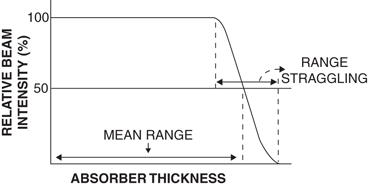
Fig. 6.3

Mean range and straggling of charged particles in an absorber

Bremsstrahlung

When energetic charged particles, particularly electrons, pass through matter and come close to the nucleus of the atom, they lose energy as a result of deceleration in the Coulomb field of atomic nuclei. The loss in energy appears as an x-ray that is called bremsstrahlung (German for “braking” or “slowing down” radiation). These bremsstrahlung radiations are commonly used in radiographic procedures and are generated by striking a tungsten target with a highly accelerated electron beam.

Bremsstrahlung production increases with the kinetic energy of the particle and the atomic number (Z) of the absorber. For example, a 10-MeV electron loses about 50 % of its energy by bremsstrahlung, whereas a 90-MeV electron loses almost 90 % of its energy by this process. The bremsstrahlung production is proportional to Z ² of the absorber atom. Therefore, bremsstrahlung is unimportant in lighter metals such as air, aluminum, and so forth, whereas it is very significant in heavy metals such as lead and tungsten. High-energy β ⁻-particles from radionuclides such as ³²P can produce bremsstrahlung in heavy metals such as lead and tungsten. For this reason, these radionuclides are stored in low-Z materials such as plastic containers rather than in lead containers.

Bremsstrahlung is inversely proportional to the mass of the charged particles and therefore is insignificant for heavy particles, namely α-particles and protons, because the probability of penetrating close to the nuclei is relatively low due to their heavier masses.

Annihilation

When energetic β ⁺-particles pass through an absorber, they lose energy via interaction with orbital electrons of the atoms of the absorber. When the β ⁺-particle comes to almost rest after losing all energy, it combines with an orbital electron of the absorber atom and produces two 511-keV annihilation radiations that are emitted in opposite directions (180°). These annihilation radiations are the basis of positron emission tomography (PET) in which two photons are detected in coincidence , which is discussed in Chap. 13.

Interaction of γ-Radiations with Matter

Mechanism of Interaction of γ-Radiations

When penetrating γ-rays pass through matter, they lose energy by interaction with the orbital electrons or the nucleus of the absorber atom. The γ-ray photons may lose all of their energy, or a fraction of it, in a single encounter. The specific ionization of γ-rays is one-tenth to one-hundredth of that caused by a non-penetrating electron of the same energy. There is no quantity equivalent to a range of particles for γ-rays, but they travel a long path in the absorber before losing all energy. The average energy loss per ion pair produced by the photons is the same as for electrons, that is, 35 keV in air.

There are several mechanisms by which γ-rays interact with absorber atoms during their passage through matter, and they are described below.

Photoelectric Effect

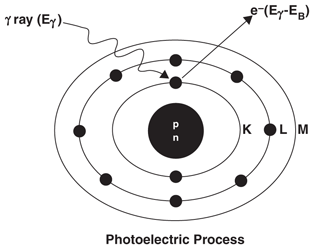
In the photoelectric effect , the incident γ-ray transfers all its energy to an orbital electron of the absorber atom whereby the electron, called the photoelectron, is ejected with kinetic energy equal to E _γ − E _B, where E _γand E _Bare the energy of the γ-ray and the binding energy of the electron, respectively (Fig. 6.4). The photoelectron loses its energy by ionization and excitation in the absorber, as discussed previously. The photoelectric effect occurs primarily in the low-energy range and decreases sharply with increasing photon energy. It also increases very rapidly with increasing atomic number Z of the absorber atom. 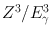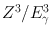Roughly, the photoelectric effect is proportional to ${Z^3}/E_\gamma ^3$ . The photoelectric contribution from the 0.15-MeV γ-rays in aluminum (Z = 13) is about the same (~ 5 %) as that from the 4.7-MeV γ-rays in lead (Z = 82).

Fig. 6.4

The photoelectric effect in which a γ-ray with energy E _γtransfers all its energy to a K-shell electron, and the electron is ejected with E _γ − E _B, where E _Bis the binding energy of the K-shell electron

The photoelectric effect occurs primarily with the K-shell electrons, with about 20 % contribution from the L-shell electrons and even less from higher shells. There are sharp increases (discontinuities) in photoelectric effects at energies exactly equal to binding energies of K-, L– (etc.) shell electrons . These are called K-, L– (etc.) absorption edges . The vacancy created by the ejection of an orbital electron is filled in by the transition of an electron from the upper energy shell. It is then followed by emission of a characteristic x-ray or Auger electron , analogous to the situations in internal conversion or electron capture decay .

Compton Scattering

In Compton scattering, the γ-ray photon transfers only a part of its energy to an electron in the outer shell of the absorber atom, and the electron is ejected. The photon, itself with reduced energy, is deflected from its original direction (Fig. 6.5). This process is called the Compton scattering . The scattered photon of lower energy may then undergo further photoelectric or Compton interaction, and the Compton electron may cause ionization or excitation, as discussed previously.

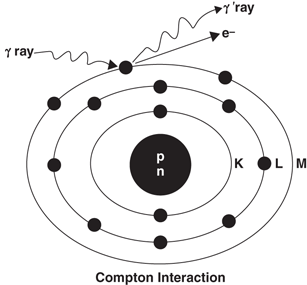
Fig. 6.5

The Compton scattering, in which a γ-ray interacts with an outer orbital electron of an absorber atom. Only a part of the photon energy is transferred to the electron, and the photon itself is scattered at an angle. The scattered photon may undergo subsequent photoelectric effect or Compton scattering in the absorber or may escape the absorber

Only gold members can continue reading. Log In or Register to continue