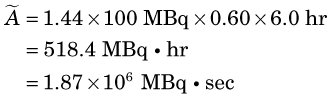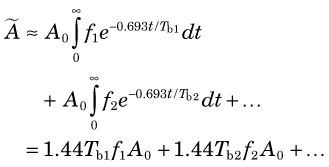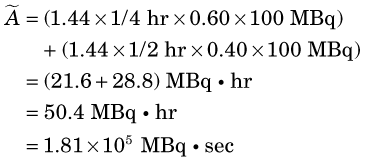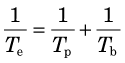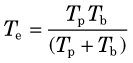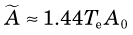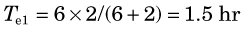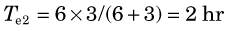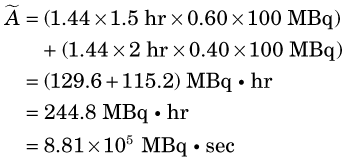chapter 22 Internal Radiation Dosimetry
Absorption of energy from ionizing radiation can cause damage to living tissues. This is used to advantage in radionuclide therapy, but it is a limitation for diagnostic applications because it is a potential hazard for the patient. In either case, it is necessary to analyze the energy distribution in body tissues quantitatively to ensure an accurate therapeutic prescription or to assess potential risks. The study of radiation effects on living organisms is the subject of radiation biology (or radiobiology) and is discussed in several excellent texts, some of which are listed at the end of this chapter.
One of the most important factors to be evaluated in the assessment of radiation effects on an organ is the amount of radiation energy deposited in that organ. Calculation of radiation energy deposited by internal radionuclides is the subject of internal radiation dosimetry. There are two general methods by which these calculations may be performed: the classic method and the absorbed fraction method. Although the classic method is somewhat simpler, and the results by the two methods are not greatly different, the absorbed fraction method (also known generally as the MIRD method, after the Medical Internal Radiation Dose Committee of the Society of Nuclear Medicine) is more versatile and gives more accurate results. Therefore it has gained wide acceptance as the standard method for performing internal dosimetry calculations. The procedures to be followed in using the absorbed fraction method are summarized in this chapter. Dosimetry calculations for external radiation sources as well as health physics aspects of radiation dosimetry are discussed in Chapter 23. Some radiation dose estimates for nuclear medicine procedures are summarized in Appendix E.
A Radiation Dose and Equivalent Dose: Quantities and Units
Radiation dose, D, refers to the quantity of radiation energy deposited in an absorber per gram of absorber material. This quantity applies to any kind of absorber material, including body tissues. The basic unit of radiation dose is the gray, abbreviated Gy*:
The traditional unit for absorbed dose is the rad, an acronym for radiation absorbed dose:
Equivalent dose, symbolically indicated by HT, is a quantity that takes into account the relative biologic damage caused by radiation interacting with a particular tissue or organ. Tissue damage per gray of absorbed dose depends on the type and energy of the radiation, and how exactly the radiation deposits its energy in the tissue. For example, an α particle has a short range in tissue and deposits all of its energy in a very localized region. In contrast, γ rays and electrons deposit their energy over a wider area. Table 22-1 shows the radiation weighting factors, wR, used to calculate equivalent dose for different types and energies of radiation. The SI unit of equivalent dose is the sievert* (Sv). It is related to the average absorbed dose D in an organ or tissue, T, by
TABLE 22-1 WEIGHTING FACTORS FOR DIFFERENT TYPES OF RADIATION IN THE CALCULATION OF EQUIVALENT DOSE†
| Type of Radiation | Radiation Weighting Factor, wR |
|---|---|
| x rays | 1 |
| γ rays | 1 |
| Electrons, positrons | 1 |
| Neutrons | Continuous function of neutron energy |
| Protons >2 MeV | 2 |
| α particles, fission fragments, heavy ions | 20 |
B Calculation of Radiation Dose (MIRD Method)
1 Basic Procedure and Some Practical Problems
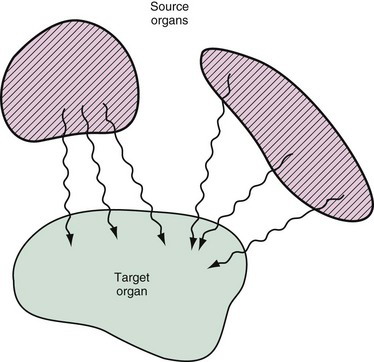
The absorbed fraction dosimetry method allows one to calculate the radiation dose delivered to a target organ from radioactivity contained in one or more source organs in the body (Fig. 22-1). The source and target may be the same organ, and, in fact, frequently the most important contributor to radiation dose is radioactivity contained within the target organ itself. Generally, organs other than the target organ are considered to be source organs if they contain concentrations of radioactivity that exceed the average concentration in the body.
Each of these steps involves certain difficulties. Step 2 involves physical characteristics of the radionuclide, which generally are known accurately. Step 3 involves patient anatomy, which can be quite different from one patient to the next. Step 1 is perhaps the most troublesome. Such data on radiopharmaceutical distribution as are available usually are obtained from studies on a relatively small number of human subjects or animals. There are variations in metabolism and distribution of radionuclides among human subjects, especially in different disease states. Also, the distribution of radioactivity within an organ may be inhomogeneous, leading to further uncertainties in the dose specification for that organ.
2 Cumulated Activity, 
Each radiotracer has its own unique spatial and temporal distribution in the body, as determined by radiotracer delivery, uptake, metabolism, clearance and excretion, and the physical decay of the radionuclide. The amount of activity contained in a source organ therefore generally changes with time. If the time-activity curve is known, the cumulated activity for a source organ is obtained by measuring the area under this curve (Fig. 22-2). Mathematically, if the time-activity curve is described by a function A(t), then
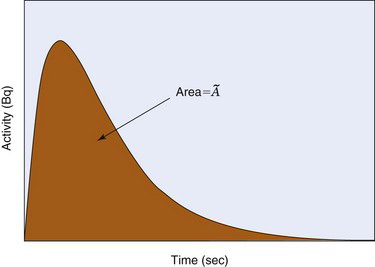
FIGURE 22-2 Hypothetical time-activity curve for radioactivity in a source organ. Cumulated activity 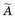 in Bq • sec is the area under the curve (equivalent to the integral in Equation 22-5).
in Bq • sec is the area under the curve (equivalent to the integral in Equation 22-5).
To estimate the radiation dose received from a particular radiotracer, time-activity curves for all the major organs are required. These can be obtained from animal studies (which are then extrapolated with some uncertainty to the human), imaging studies in normal human subjects, prior knowledge of the tracer kinetics, or some combination of these approaches. Time-activity curves can be quite complex, and thus Equation 22-5 may be difficult to analyze. Frequently, however, certain assumptions can be made to simplify this calculation.
Situation 1: Uptake by the organ is “instantaneous” (i.e., very rapid with respect to the half-life of the radionuclide), and there is no biologic excretion. The time-activity curve then is described by ordinary radioactive decay (Equations 4-7 and 4-10):
The quantity 1.44Tp is the average lifetime of the radionuclide (see Chapter 4, Section B.3). Thus the cumulated activity in a source organ, when eliminated by physical decay only, is the same as if activity were present at a constant level A0 for a time equal to the average lifetime of the radionuclide (Fig. 22-3).
Answer
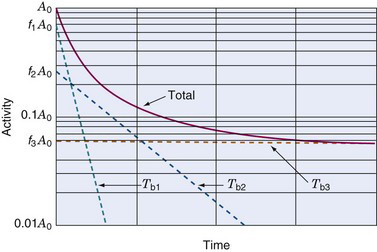
Situation 2: Uptake is instantaneous, and clearance is by biologic excretion only (no physical decay, or physical half-life very long in comparison with biologic excretion). In this situation, biologic excretion must be carefully analyzed. Frequently, it can be described by a set of exponential excretion components, with a fraction f1 of the initial activity A 0 being excreted with a (biologic) half-life Tb1, a fraction f2 with half-life Tb2, and so on (Fig. 22-4). The cumulated activity then is given by
Example 22-2
Suppose that 100 MBq of 99mTc-labeled microspheres are injected into a patient, with essentially instantaneous uptake of activity by the lungs. What is the cumulated activity in the lungs if 60% of the activity is excreted from the lungs with a biologic half-life of 15 minutes and 40% with a biologic half-life of 30 minutes?
Answer
Because 99mTc physical decay is much slower than the biologic excretion process, we may assume that no physical decay occurs during the time that activity is present in the lungs. Thus (Equation 22-8)
Situation 3: Uptake is instantaneous but clearance by both physical decay and biologic excretion are significant. In this case, if biologic excretion is described by a single-component exponential curve with biologic half-life Tb, and the physical half-life is Tp, then the total clearance is described by a single-component exponential curve with an effective half-life Te given by*
Cumulated activity is given by
If there is more than one component to the biologic excretion curve, then each component has an effective half-life given by Equation 22-9 for that component, and the cumulated activity is computed with effective half-lives replacing biologic half-lives in Equation 22-8.
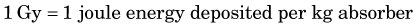
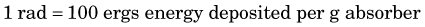
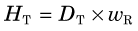
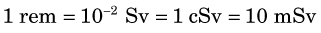
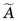 in the source organ. The SI unit for cumulated activity is the becquerel • sec (Bq • sec). The corresponding traditional unit is the µCi • hr (1 µCi = 3.7 × 104 Bq; 1 hr = 3600 sec; therefore, 1 µCi • hr = 3.7 × 104 × 3600 = 1.332 × 108 Bq • sec = 1.332 × 102 MBq • sec). Cumulated activity is essentially a measure of the total number of radioactive disintegrations occurring during the time that radioactivity is present in the source organ. The radiation dose delivered by activity in a source organ is proportional to its cumulated activity.
in the source organ. The SI unit for cumulated activity is the becquerel • sec (Bq • sec). The corresponding traditional unit is the µCi • hr (1 µCi = 3.7 × 104 Bq; 1 hr = 3600 sec; therefore, 1 µCi • hr = 3.7 × 104 × 3600 = 1.332 × 108 Bq • sec = 1.332 × 102 MBq • sec). Cumulated activity is essentially a measure of the total number of radioactive disintegrations occurring during the time that radioactivity is present in the source organ. The radiation dose delivered by activity in a source organ is proportional to its cumulated activity.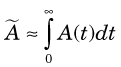
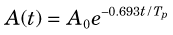
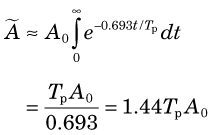
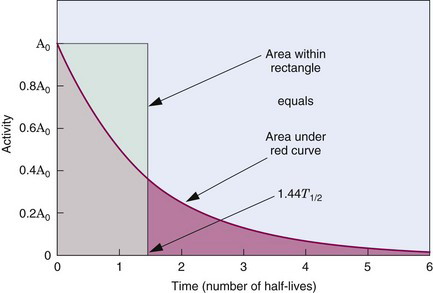
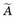 and average lifetime (1.44 Tp) of a radionuclide for simple exponential decay.
and average lifetime (1.44 Tp) of a radionuclide for simple exponential decay.