Here,
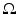 is the image domain,
is the image domain, 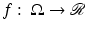 is the observed noisy image, u:
is the observed noisy image, u: 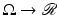 is the denoised image, and μ ≥ 0 is a parameter depending on the noise level. The first term is the total variation (TV) which is a measure of the amount of oscillation in the resulting image u. Its minimization would reduce the amount of oscillation which presumably reduces noise. The second term is the L 2 distance between u and f, which encourages the denoised image to inherit most features from the observed data. Thus, the model trades off the closeness to f by gaining the regularity of u. The noise is assumed to be additive and Gaussian with zero mean. If the noise variance level σ 2 is known, then the parameter μ can be treated as the Lagrange multiplier, restraining the resulting image to be consistent with the known noise level, i.e.,
is the denoised image, and μ ≥ 0 is a parameter depending on the noise level. The first term is the total variation (TV) which is a measure of the amount of oscillation in the resulting image u. Its minimization would reduce the amount of oscillation which presumably reduces noise. The second term is the L 2 distance between u and f, which encourages the denoised image to inherit most features from the observed data. Thus, the model trades off the closeness to f by gaining the regularity of u. The noise is assumed to be additive and Gaussian with zero mean. If the noise variance level σ 2 is known, then the parameter μ can be treated as the Lagrange multiplier, restraining the resulting image to be consistent with the known noise level, i.e., 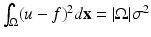 [16].
[16].The ROF model is simple and elegant for edge-preserving denoising. Since its introduction, this model has ignited a great deal of research in constructing more sophisticated variants which can give better reconstructed images, designing faster numerical algorithms for solving the optimization problem numerically, and finding new applications in various domains. In a previous book chapter [21] published in 2005, the authors surveyed some recent progresses in the research of total variation-based models. The present chapter aims at highlighting some exciting latest developments in numerical methods and applications of total variation-based methods since the last survey.
3 Mathematical Modeling and Analysis
In this section, the basic definition of total variation and some of its variants are presented. Then, some recent TV-based mathematical models in imaging are reviewed.
Variants of Total Variation
Basic Definition
The use of TV as a regularizer has been shown to be very effective for processing images because of its ability to preserve edges. Being introduced for different reasons, several variants of TV can be found in the literature. Some variants can handle more sophisticated data such as vector-valued imagery and matrix-valued tensors; some are designed to improve restoration quality, and some are modified versions for the ease of numerical implementation. It is worthwhile to review the basic definition and its variants.
In Rudin, Osher, and Fatemi’s work [51], the TV of an image 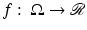 is defined as
is defined as
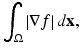 where
where 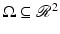 is a bounded open set. Since the image f may contain discontinuities, the gradient ∇f must be interpreted in a generalized sense. It is well known that elements of the Sobolev space
is a bounded open set. Since the image f may contain discontinuities, the gradient ∇f must be interpreted in a generalized sense. It is well known that elements of the Sobolev space 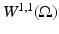 cannot have discontinuities [2]. Therefore, the TV cannot be defined through the completion of the space C 1 of continuously differentiable functions under the Sobolev norm. The ∇f is thus interpreted as a distributional derivative, and its integral is interpreted as a distributional integral [40]. Under this framework, the minimization of TV naturally leads to a PDE with a distribution as a solution.
cannot have discontinuities [2]. Therefore, the TV cannot be defined through the completion of the space C 1 of continuously differentiable functions under the Sobolev norm. The ∇f is thus interpreted as a distributional derivative, and its integral is interpreted as a distributional integral [40]. Under this framework, the minimization of TV naturally leads to a PDE with a distribution as a solution.
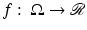 is defined as
is defined as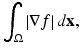
 is a bounded open set. Since the image f may contain discontinuities, the gradient ∇f must be interpreted in a generalized sense. It is well known that elements of the Sobolev space
is a bounded open set. Since the image f may contain discontinuities, the gradient ∇f must be interpreted in a generalized sense. It is well known that elements of the Sobolev space 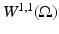 cannot have discontinuities [2]. Therefore, the TV cannot be defined through the completion of the space C 1 of continuously differentiable functions under the Sobolev norm. The ∇f is thus interpreted as a distributional derivative, and its integral is interpreted as a distributional integral [40]. Under this framework, the minimization of TV naturally leads to a PDE with a distribution as a solution.
cannot have discontinuities [2]. Therefore, the TV cannot be defined through the completion of the space C 1 of continuously differentiable functions under the Sobolev norm. The ∇f is thus interpreted as a distributional derivative, and its integral is interpreted as a distributional integral [40]. Under this framework, the minimization of TV naturally leads to a PDE with a distribution as a solution.Besides defining TV as a distributional integral, other perspectives can offer some unique advantages. A set theoretical way is to define TV as a Radon measure of the domain  [50]. This has an advantage of allowing
[50]. This has an advantage of allowing  to be a more general set. But a more practical and simple alternative is the “dual formulation.” It uses the usual trick in defining weak derivatives – integration by parts – together with the Fenchel transform,
to be a more general set. But a more practical and simple alternative is the “dual formulation.” It uses the usual trick in defining weak derivatives – integration by parts – together with the Fenchel transform,
where 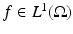 and div is the divergence operator. Using this definition, one can bypass the discussion of distributions. It also plays an important role in many recent works in dual and primal-dual methods for solving TV minimization problems. The space BV can now be defined as
and div is the divergence operator. Using this definition, one can bypass the discussion of distributions. It also plays an important role in many recent works in dual and primal-dual methods for solving TV minimization problems. The space BV can now be defined as
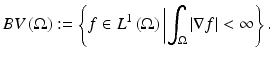 Equipped with the norm
Equipped with the norm 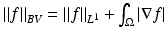 , this space is complete and is a proper superset of
, this space is complete and is a proper superset of 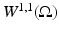 [32].
[32].
 [50]. This has an advantage of allowing
[50]. This has an advantage of allowing 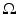 to be a more general set. But a more practical and simple alternative is the “dual formulation.” It uses the usual trick in defining weak derivatives – integration by parts – together with the Fenchel transform,
to be a more general set. But a more practical and simple alternative is the “dual formulation.” It uses the usual trick in defining weak derivatives – integration by parts – together with the Fenchel transform,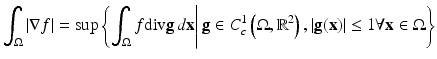
(1)
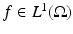 and div is the divergence operator. Using this definition, one can bypass the discussion of distributions. It also plays an important role in many recent works in dual and primal-dual methods for solving TV minimization problems. The space BV can now be defined as
and div is the divergence operator. Using this definition, one can bypass the discussion of distributions. It also plays an important role in many recent works in dual and primal-dual methods for solving TV minimization problems. The space BV can now be defined as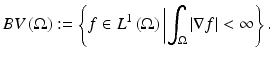
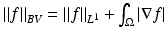 , this space is complete and is a proper superset of
, this space is complete and is a proper superset of 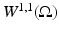 [32].
[32].Multichannel TV
Many practical images are acquired in a multichannel way, where each channel emphasizes a specific kind of signal. For example, color images are often acquired through the RGB color components, whereas microscopy images consist of measurements of different fluorescent labels. The signals in the different channels are often correlated (contain redundant information). Therefore, in many practical situations, regularization of multichannel images should not be done independently on each channel.
There are several existing ways to generalize TV to vectorial data. A review of some generalizations can be found in [20]. Many generalizations are very intuitive. But only some of them have a natural dual formulation. Sapiro and Ringach [52] proposed to define
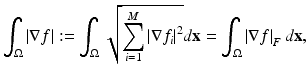 where
where 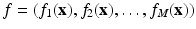 is the vectorial data with M channels. Thus, it is the integral of the Frobenius norm
is the vectorial data with M channels. Thus, it is the integral of the Frobenius norm 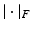 of the Jacobian ∇f. The dual formulation given in [10] is
of the Jacobian ∇f. The dual formulation given in [10] is
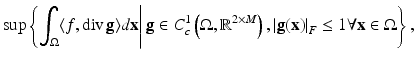 where
where 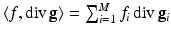 .
.
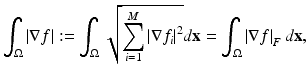
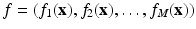 is the vectorial data with M channels. Thus, it is the integral of the Frobenius norm
is the vectorial data with M channels. Thus, it is the integral of the Frobenius norm 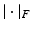 of the Jacobian ∇f. The dual formulation given in [10] is
of the Jacobian ∇f. The dual formulation given in [10] is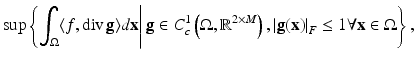
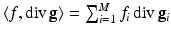 .
.Matrix-Valued TV
In applications such as diffusion tensor imaging (DTI), the measurements at each spatial location are represented by a diffusion tensor, which is a 3 × 3 symmetric positive semi-definite matrix. Recent efforts have been devoted to generalize the TV to matrix-valued images. Some natural generalizations can be obtained by identifying an M × N matrix with an MN vector, so that a vector-valued total variation can be applied. This was done by Tschumperlé and Deriche [57], who generalized the vectorial TV of [7]. The main challenge is to preserve the positive definiteness of the denoised solution. This will be elaborated in section “Diffusion Tensors Images.”
Another interesting approach proposed by Setzer et al. [54] is the so-called operator-based regularization. Given a matrix-valued function 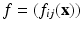 , define a matrix function A: = (a ij ) where
, define a matrix function A: = (a ij ) where 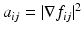 . Let Φ(A) be the matrix obtained by replacing each eigenvalue λ of A with
. Let Φ(A) be the matrix obtained by replacing each eigenvalue λ of A with 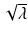 . Then the total variation is defined to be
. Then the total variation is defined to be 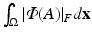 , where
, where 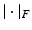 is the Frobenius norm. While this formulation seems complicated, its first variation turns out to have a nice simple formula. However, when combined with the ROF model, the preservation of positive definiteness is an issue.
is the Frobenius norm. While this formulation seems complicated, its first variation turns out to have a nice simple formula. However, when combined with the ROF model, the preservation of positive definiteness is an issue.
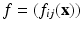 , define a matrix function A: = (a ij ) where
, define a matrix function A: = (a ij ) where 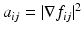 . Let Φ(A) be the matrix obtained by replacing each eigenvalue λ of A with
. Let Φ(A) be the matrix obtained by replacing each eigenvalue λ of A with 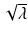 . Then the total variation is defined to be
. Then the total variation is defined to be 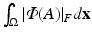 , where
, where 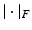 is the Frobenius norm. While this formulation seems complicated, its first variation turns out to have a nice simple formula. However, when combined with the ROF model, the preservation of positive definiteness is an issue.
is the Frobenius norm. While this formulation seems complicated, its first variation turns out to have a nice simple formula. However, when combined with the ROF model, the preservation of positive definiteness is an issue.Discrete TV
The ROF model is cast as an infinite-dimensional optimization problem over the BV space. To solve the problem numerically, one must discretize the problem at some stage. The approach proposed by Rudin et al. in [51] is to “optimize then discretize.” The gradient flow equation is discretized with a standard finite difference scheme. This method works very well in the sense that the numerical solution converges to a steady state which is qualitatively consistent with the expected result of the (continuous) ROF model. However, to the best of the authors’ knowledge, a theoretical proof of convergence of the numerical solution to the exact solution of the gradient flow equation as the grid size tends to zero is not yet available. A standard convergence result of finite difference schemes for nonlinear PDE is based on the compactness of TV-bounded sets in L 1 [46]. However, proving TV boundedness in two or more dimensions is often difficult.
An alternative approach is to “discretize then optimize.” In this case, only one has to solve a finite-dimensional optimization problem, whose numerical solution can in many cases be shown to converge. But the convergence of the exact solution of the finite-dimensional problems to the exact solution of the original infinite-dimensional problem is often hard to obtain too. So, both approaches suffer from the theoretical convergence problem. But the latter method has a precise discrete objective to optimize.
To discretize the ROF objective, the fitting term is often straightforward. But the discretization of the TV term has a strong effect on the numerical schemes. The most commonly used versions of discrete TV are
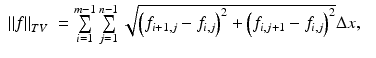
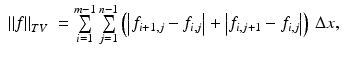
where f = (f i, j ) is the discrete image and 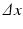 is the grid size. They are sometimes referred as the isotropic and anisotropic versions, respectively, for they are a formal discretization of the isotropic TV
is the grid size. They are sometimes referred as the isotropic and anisotropic versions, respectively, for they are a formal discretization of the isotropic TV 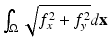 and the anisotropic TV
and the anisotropic TV 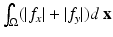 , respectively. The anisotropic TV is not rotational invariant; an image and its rotation can have a different TV value. Therefore, the discrete TV (3) deviates from the original isotropic TV. But being a piecewise linear function, some numerical techniques for quadratic and linear problems can be applied. Indeed, by introducing some auxiliary variables, the corresponding discrete ROF objective can be converted into a canonical quadratic programming problem [30].
, respectively. The anisotropic TV is not rotational invariant; an image and its rotation can have a different TV value. Therefore, the discrete TV (3) deviates from the original isotropic TV. But being a piecewise linear function, some numerical techniques for quadratic and linear problems can be applied. Indeed, by introducing some auxiliary variables, the corresponding discrete ROF objective can be converted into a canonical quadratic programming problem [30].
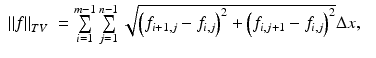
(2)
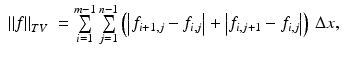
(3)
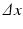 is the grid size. They are sometimes referred as the isotropic and anisotropic versions, respectively, for they are a formal discretization of the isotropic TV
is the grid size. They are sometimes referred as the isotropic and anisotropic versions, respectively, for they are a formal discretization of the isotropic TV 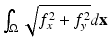 and the anisotropic TV
and the anisotropic TV 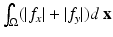 , respectively. The anisotropic TV is not rotational invariant; an image and its rotation can have a different TV value. Therefore, the discrete TV (3) deviates from the original isotropic TV. But being a piecewise linear function, some numerical techniques for quadratic and linear problems can be applied. Indeed, by introducing some auxiliary variables, the corresponding discrete ROF objective can be converted into a canonical quadratic programming problem [30].
, respectively. The anisotropic TV is not rotational invariant; an image and its rotation can have a different TV value. Therefore, the discrete TV (3) deviates from the original isotropic TV. But being a piecewise linear function, some numerical techniques for quadratic and linear problems can be applied. Indeed, by introducing some auxiliary variables, the corresponding discrete ROF objective can be converted into a canonical quadratic programming problem [30].Besides using finite difference approximations, a recent popular way is to represent TV on graphs [27]. To make the problem fully discrete, the range of the image is quantized to a finite set of K integers only, usually 0–255. The image is “leveled,” so that 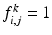 if the intensity of the (i, j)th pixel is at most k, and
if the intensity of the (i, j)th pixel is at most k, and 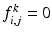 otherwise. Then, the TV is given by
otherwise. Then, the TV is given by
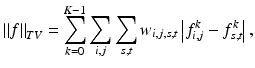
where w i, j, s, t is a nonnegative weight. A simple choice is the four-connectivity model, where 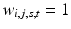 if
if 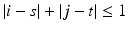 and w i, j, s, t = 0 otherwise. In this case, it becomes the anisotropic TV (3). Different choices of the weights penalize edges in different orientations.
and w i, j, s, t = 0 otherwise. In this case, it becomes the anisotropic TV (3). Different choices of the weights penalize edges in different orientations.
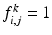 if the intensity of the (i, j)th pixel is at most k, and
if the intensity of the (i, j)th pixel is at most k, and 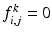 otherwise. Then, the TV is given by
otherwise. Then, the TV is given by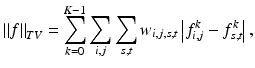
(4)
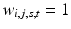 if
if 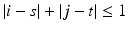 and w i, j, s, t = 0 otherwise. In this case, it becomes the anisotropic TV (3). Different choices of the weights penalize edges in different orientations.
and w i, j, s, t = 0 otherwise. In this case, it becomes the anisotropic TV (3). Different choices of the weights penalize edges in different orientations.A related concept introduced by Shen and Kang is the quantum total variation [55]. They studied the ROF model when the range of an image is a finite discrete set (preassigned or determined on the fly), but the image domain is a continuous one. The model is suitable for problems such as bar code scanning, image quantization, and image segmentation. An elegant analysis of the model and some stochastic gradient descent algorithms were presented there.
Nonlocal TV
First proposed by Buades et al. [11], the nonlocal means algorithm renounces the use of local smoothness to denoise an image. Patches which are spatially far away but photometrically similar are also utilized in the estimation process – a paradigm which has been used in texture synthesis [28]. The denoising results are surprisingly good. Since then, the use of nonlocal information becomes increasingly popular. In particular, Bresson and Chan [10] and Gilboa and Osher [31] considered the nonlocal TV. The nonlocal gradient ∇ NL f for a pair of points 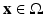 and
and 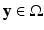 is defined by
is defined by
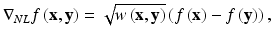 where w(x, y) is a nonnegative weight function which is presumably a similarity measure between a patch around x and a patch around y. As an illustration, a simple choice of the weight function is
where w(x, y) is a nonnegative weight function which is presumably a similarity measure between a patch around x and a patch around y. As an illustration, a simple choice of the weight function is
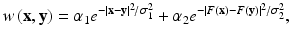 where α i and σ i are positive constants, and F(x) is a feature vector derived from a patch around x. The constants α i may sometimes be defined to depend on x, so that the total weight over all
where α i and σ i are positive constants, and F(x) is a feature vector derived from a patch around x. The constants α i may sometimes be defined to depend on x, so that the total weight over all 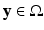 is normalized to 1. In this case, the weight function is nonsymmetric with respective to its arguments. The first term in w is a measure of geometric similarity, so that nearby pixels have a higher weight. The second term is a measure of photometric similarity. The feature vector F can be the color histogram or any texture descriptor over a window around x. The norm of the nonlocal gradient at x is defined by
is normalized to 1. In this case, the weight function is nonsymmetric with respective to its arguments. The first term in w is a measure of geometric similarity, so that nearby pixels have a higher weight. The second term is a measure of photometric similarity. The feature vector F can be the color histogram or any texture descriptor over a window around x. The norm of the nonlocal gradient at x is defined by
![$$\displaystyle{\left \vert \nabla _{NL}f\left ({\mathbf{x}}\right )\right \vert = \sqrt{\int _{\Omega } \left [\nabla _{NL } f\left (\mathbf{x, y } \right ) \right ] ^{2 } d\mathbf{y}},}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equh.gif) which adds up all the squared intensity variation relative to f(x), weighted by the similarity between the corresponding pair of patches. The nonlocal TV is then naturally defined by summing up all the norms of the nonlocal gradients over the image domain:
which adds up all the squared intensity variation relative to f(x), weighted by the similarity between the corresponding pair of patches. The nonlocal TV is then naturally defined by summing up all the norms of the nonlocal gradients over the image domain:
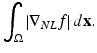 Therefore, the nonlocal TV is small if, for each pair of similar patches, the intensity difference between their centers is small. An advantage of using the nonlocal TV to regularize images is its tendency to preserve highly repetitive patterns better. In practice, the weight function is often truncated to reduce the computation costs spent in handling the many less similar patches.
Therefore, the nonlocal TV is small if, for each pair of similar patches, the intensity difference between their centers is small. An advantage of using the nonlocal TV to regularize images is its tendency to preserve highly repetitive patterns better. In practice, the weight function is often truncated to reduce the computation costs spent in handling the many less similar patches.
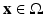 and
and 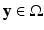 is defined by
is defined by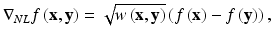
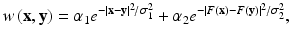
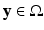 is normalized to 1. In this case, the weight function is nonsymmetric with respective to its arguments. The first term in w is a measure of geometric similarity, so that nearby pixels have a higher weight. The second term is a measure of photometric similarity. The feature vector F can be the color histogram or any texture descriptor over a window around x. The norm of the nonlocal gradient at x is defined by
is normalized to 1. In this case, the weight function is nonsymmetric with respective to its arguments. The first term in w is a measure of geometric similarity, so that nearby pixels have a higher weight. The second term is a measure of photometric similarity. The feature vector F can be the color histogram or any texture descriptor over a window around x. The norm of the nonlocal gradient at x is defined by![$$\displaystyle{\left \vert \nabla _{NL}f\left ({\mathbf{x}}\right )\right \vert = \sqrt{\int _{\Omega } \left [\nabla _{NL } f\left (\mathbf{x, y } \right ) \right ] ^{2 } d\mathbf{y}},}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equh.gif)
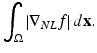
Further Applications
Inpainting in Transformed Domains
After the release of the image compression standard JPEG2000, images can be formatted and stored in terms of wavelet coefficients. For instance, in Acrobat 6.0 or later, users can opt to use JPEG2000 to compress embedded images in a PDF file. During the process of storing or transmission, some wavelet coefficients may be lost or corrupted. This prompts the need of restoring missing information in wavelet domains. The setup of the problem is as follows. Denote the standard orthogonal wavelet expansion of the images f and u by
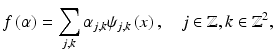 and
and
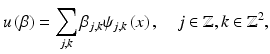 where
where 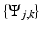 is the wavelet basis, and
is the wavelet basis, and 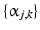 ,
, 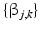 are the wavelet coefficients of f and u given by
are the wavelet coefficients of f and u given by
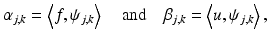 respectively, for
respectively, for 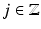 ,
, 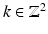 . For convenience,
. For convenience, 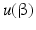 is denoted by u when there is no ambiguity. Assume that the wavelet coefficients in the index set I are known, i.e., the available wavelet coefficients are given by
is denoted by u when there is no ambiguity. Assume that the wavelet coefficients in the index set I are known, i.e., the available wavelet coefficients are given by
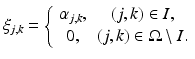 The aim of wavelet domain inpainting is to reconstruct the wavelet coefficients of u from the given coefficients
The aim of wavelet domain inpainting is to reconstruct the wavelet coefficients of u from the given coefficients 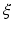 . It is well known that the inpainting problem is ill posed, i.e., it admits more than one solution. There are many different ways to fill in the missing coefficients, and therefore many different reconstructions in the pixel domain are possible. Regularization methods can be used to incorporate prior information about the reconstruction. In [23], Chan, Shen, and Zhou used TV to solve the wavelet inpainting problem, so that the missing coefficients are filled while preserving sharp edges in the pixel domain faithfully. More precisely, they considered the minimization of the following objective
. It is well known that the inpainting problem is ill posed, i.e., it admits more than one solution. There are many different ways to fill in the missing coefficients, and therefore many different reconstructions in the pixel domain are possible. Regularization methods can be used to incorporate prior information about the reconstruction. In [23], Chan, Shen, and Zhou used TV to solve the wavelet inpainting problem, so that the missing coefficients are filled while preserving sharp edges in the pixel domain faithfully. More precisely, they considered the minimization of the following objective
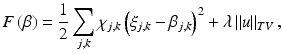
with 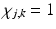 if (j, k) ∈ I and
if (j, k) ∈ I and 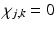 if
if 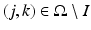 , and λ is the regularization parameter. The first term in F is the data-fitting term, and the second is the TV regularization term. The method Chan, Shen, and Zhou used to optimize the objective is the standard gradient descent. The method is very robust, but it often slows down significantly before it converges.
, and λ is the regularization parameter. The first term in F is the data-fitting term, and the second is the TV regularization term. The method Chan, Shen, and Zhou used to optimize the objective is the standard gradient descent. The method is very robust, but it often slows down significantly before it converges.
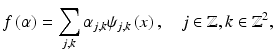
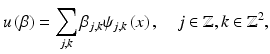
 is the wavelet basis, and
is the wavelet basis, and 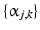 ,
, 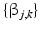 are the wavelet coefficients of f and u given by
are the wavelet coefficients of f and u given by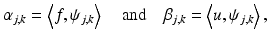
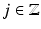 ,
, 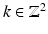 . For convenience,
. For convenience, 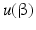 is denoted by u when there is no ambiguity. Assume that the wavelet coefficients in the index set I are known, i.e., the available wavelet coefficients are given by
is denoted by u when there is no ambiguity. Assume that the wavelet coefficients in the index set I are known, i.e., the available wavelet coefficients are given by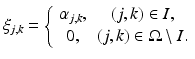
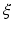 . It is well known that the inpainting problem is ill posed, i.e., it admits more than one solution. There are many different ways to fill in the missing coefficients, and therefore many different reconstructions in the pixel domain are possible. Regularization methods can be used to incorporate prior information about the reconstruction. In [23], Chan, Shen, and Zhou used TV to solve the wavelet inpainting problem, so that the missing coefficients are filled while preserving sharp edges in the pixel domain faithfully. More precisely, they considered the minimization of the following objective
. It is well known that the inpainting problem is ill posed, i.e., it admits more than one solution. There are many different ways to fill in the missing coefficients, and therefore many different reconstructions in the pixel domain are possible. Regularization methods can be used to incorporate prior information about the reconstruction. In [23], Chan, Shen, and Zhou used TV to solve the wavelet inpainting problem, so that the missing coefficients are filled while preserving sharp edges in the pixel domain faithfully. More precisely, they considered the minimization of the following objective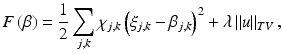
(5)
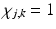 if (j, k) ∈ I and
if (j, k) ∈ I and 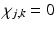 if
if 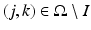 , and λ is the regularization parameter. The first term in F is the data-fitting term, and the second is the TV regularization term. The method Chan, Shen, and Zhou used to optimize the objective is the standard gradient descent. The method is very robust, but it often slows down significantly before it converges.
, and λ is the regularization parameter. The first term in F is the data-fitting term, and the second is the TV regularization term. The method Chan, Shen, and Zhou used to optimize the objective is the standard gradient descent. The method is very robust, but it often slows down significantly before it converges.In [18], Chan, Wen, and Yip proposed an efficient optimization transfer algorithm to minimize the objective (5). An auxiliary variable ζ is introduced to yield a new objective function:
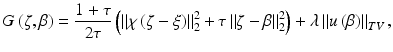 where
where 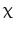 denotes a diagonal matrix with diagonal entries χ j, k , and τ is an arbitrary positive parameter. The function G is a quadratic majorizing function [43] of F. The method also has a flavor of the splitting methods introduced in section “Splitting Methods.” But a major difference is that the method here solves the original problem (5) without any alteration. It can be easily shown that
denotes a diagonal matrix with diagonal entries χ j, k , and τ is an arbitrary positive parameter. The function G is a quadratic majorizing function [43] of F. The method also has a flavor of the splitting methods introduced in section “Splitting Methods.” But a major difference is that the method here solves the original problem (5) without any alteration. It can be easily shown that
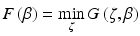 for any positive regularization parameter τ. Thus, the minimization of G w.r.t.
for any positive regularization parameter τ. Thus, the minimization of G w.r.t. 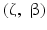 is equivalent to the minimization of F w.r.t.
is equivalent to the minimization of F w.r.t. 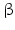 for any
for any ![$$\uptau > 0$$” src=”/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_IEq44.gif”></SPAN>. Unlike the gradient descent method of [<CITE><A href=]() 23], the optimization transfer algorithm avoids the use of derivatives of the TV. It also does not require smoothing out the TV to make it differentiable. The experimental results in [18] showed that the algorithm is very efficient and outperforms the gradient descent method.
23], the optimization transfer algorithm avoids the use of derivatives of the TV. It also does not require smoothing out the TV to make it differentiable. The experimental results in [18] showed that the algorithm is very efficient and outperforms the gradient descent method.
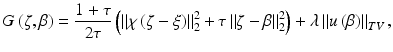
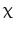 denotes a diagonal matrix with diagonal entries χ j, k , and τ is an arbitrary positive parameter. The function G is a quadratic majorizing function [43] of F. The method also has a flavor of the splitting methods introduced in section “Splitting Methods.” But a major difference is that the method here solves the original problem (5) without any alteration. It can be easily shown that
denotes a diagonal matrix with diagonal entries χ j, k , and τ is an arbitrary positive parameter. The function G is a quadratic majorizing function [43] of F. The method also has a flavor of the splitting methods introduced in section “Splitting Methods.” But a major difference is that the method here solves the original problem (5) without any alteration. It can be easily shown that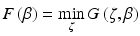
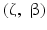 is equivalent to the minimization of F w.r.t.
is equivalent to the minimization of F w.r.t. 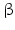 for any
for any Superresolution
Image superresolution refers to the process of increasing spatial resolution by fusing information from a sequence of low-resolution images of the same scene. The images are assumed to contain subpixel information (due to subpixel displacements or blurring), so that the superresolution is possible.
In [24], Chan et al. proposed a unified TV model for superresolution imaging problems. They focused on the problem of reconstructing a high-resolution image from several decimated, blurred, and noisy low-resolution versions of the high-resolution image. They derived a low-resolution image formation model which allows multiple-shifted and blurred low-resolution image frames, so that it subsumes several well-known models. The model also allows an arbitrary pattern of missing pixels (in particular an arbitrary pattern of missing frames). The superresolution image reconstruction problem is formulated as an optimization problem which combines the image formation model and the TV inpainting model. In this method, TV minimization is used to suppress noise amplification, repair corrupted pixels in regions without missing pixels, and reconstruct intensity levels in regions with missing pixels.
Image Formation Model
The observation model, Chan et al. considered, consists of various degradation processes. Assume that a number of m × n low-resolution frames are captured by an array of charge-coupled device (CCD) sensors. The goal is to reconstruct an 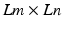 high-resolution image. Thus, the resolution is increased by a factor of L in each dimension. Let u be the ideal Lm ×Ln high-resolution clean image.
high-resolution image. Thus, the resolution is increased by a factor of L in each dimension. Let u be the ideal Lm ×Ln high-resolution clean image.
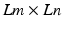 high-resolution image. Thus, the resolution is increased by a factor of L in each dimension. Let u be the ideal Lm ×Ln high-resolution clean image.
high-resolution image. Thus, the resolution is increased by a factor of L in each dimension. Let u be the ideal Lm ×Ln high-resolution clean image.1.
Formation of low-resolution frames. A low-resolution frame is given by
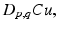 where C is an averaging filter with window size L-by-L, and D p, q is the downsampling matrix which, starting at the (p, q)th pixel, samples every other L pixels in both dimensions to form an m × n image.
where C is an averaging filter with window size L-by-L, and D p, q is the downsampling matrix which, starting at the (p, q)th pixel, samples every other L pixels in both dimensions to form an m × n image.
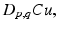
2.
Blurring of frames. This is modeled by
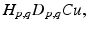 where H p, q is the blurring matrix for the (p, q)th frame.
where H p, q is the blurring matrix for the (p, q)th frame.
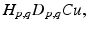
3.
Concatenation of frames. The full set of L 2 frames are interlaced to form an mL ×nL image:
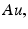 where
where
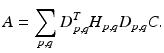
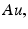
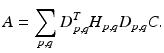
4.
Additive Noise.
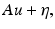 where each pixel in η is a Gaussian white noise.
where each pixel in η is a Gaussian white noise.
5.
Missing pixels and missing frames.
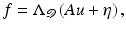 where
where 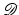 denotes the set of missing pixels, and
denotes the set of missing pixels, and 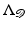 is the downsampling matrix from the image domain to
is the downsampling matrix from the image domain to 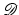 .
.
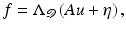
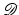 denotes the set of missing pixels, and
denotes the set of missing pixels, and 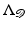 is the downsampling matrix from the image domain to
is the downsampling matrix from the image domain to 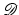 .
.6.
Multiple observations. Finally, multiple observations of the same scene, but with different noise and blurring, are allowed. This leads to the model
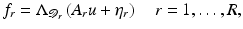
where
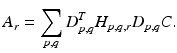
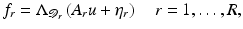
(6)
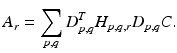
TV Superresolution Imaging Model
To invert the degradation processes in (6), a Tikhonov-type regularization model has been used. It requires minimization of the following energy:
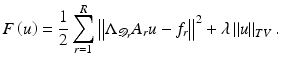 This model simultaneously performs denoising, deblurring, inpainting, and superresolution reconstruction. Experimental results show that reasonably good reconstruction can be obtained even if five-sixth of the pixels are missing and the frames are blurred.
This model simultaneously performs denoising, deblurring, inpainting, and superresolution reconstruction. Experimental results show that reasonably good reconstruction can be obtained even if five-sixth of the pixels are missing and the frames are blurred.
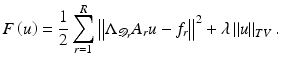
Image Segmentation
TV minimization problems also arise from image segmentation. When one seeks for a partition of the image into homogeneous segments, it is often helpful to regularize the shape of the segments. This can increase the robustness of the algorithm against noise and avoid spurious segments. It may also allow the selection of features of different scales. In the classical Mumford-Shah model [47], the regularization is done by minimizing the total length of the boundary of the segments. In this case, if one represents a segment by its characteristic function, then the length of its boundary is exactly the TV of the characteristic function. Therefore, the minimization of length becomes the minimization of TV of characteristic functions.
Given an observed image f on an image domain 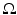 , the piecewise constant Mumford-Shah model seeks a set of curves C and a set of constant
, the piecewise constant Mumford-Shah model seeks a set of curves C and a set of constant  which minimize the energy functional given by
which minimize the energy functional given by
![$$\displaystyle{ F^{MS}\left (C,\mathbf{c}\right ) =\sum \limits _{ l=1}^{L}\int _{ \Omega _{l}}\left [f\left ({\mathbf{x}}\right ) - c_{l}\right ]^{2}d{\mathbf{x}} +\beta \cdot \text{Length}\left (C\right ). }$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equx.gif) The curves in C partition the image into L mutually exclusive segments
The curves in C partition the image into L mutually exclusive segments 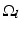 for
for 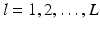 . The idea is to partition the image, so that the intensity of f in each segment
. The idea is to partition the image, so that the intensity of f in each segment 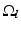 is well approximated by a constant c l . The goodness of fit is measured by the L 2 difference between f and c l . On the other hand, a minimum description length principle is employed which requires the curves C to be as short as possible. This increases the robustness to noise and avoids spurious segments. The parameter
is well approximated by a constant c l . The goodness of fit is measured by the L 2 difference between f and c l . On the other hand, a minimum description length principle is employed which requires the curves C to be as short as possible. This increases the robustness to noise and avoids spurious segments. The parameter ![$$\upbeta > 0$$” src=”/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_IEq54.gif”></SPAN> controls the trade-off between the goodness of fit and the length of the curves <SPAN class=EmphasisTypeItalic>C</SPAN>. The Mumford-Shah objective is nontrivial to optimize especially when the curves need to be split and merged. Chan and Vese [<CITE><A href=]() 24] proposed a level set-based method which can handle topological changes effectively. In the two-phase version of this method, the curves are represented by the zero level set of a Lipschitz level set function
24] proposed a level set-based method which can handle topological changes effectively. In the two-phase version of this method, the curves are represented by the zero level set of a Lipschitz level set function 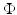 defined on the image domain. The objective function then becomes
defined on the image domain. The objective function then becomes
![$$\displaystyle{\begin{array}{rl} F^{{\mathrm{CV}}}\left (\phi,c_{ 1},c_{2}\right )& =\int _{\Omega }H\left (\phi \left ({\mathbf{x}}\right )\right )\left [f\left ({\mathbf{x}}\right ) - c_{1}\right ]^{2}d{\mathbf{x}} \\ &\quad +\int _{\Omega }\left [1 - H\left (\phi \left ({\mathbf{x}}\right )\right )\right ]\left [f\left ({\mathbf{x}}\right ) - c_{2}\right ]^{2}d{\mathbf{x}} +\beta \int _{ \Omega }\left \vert \nabla H\left (\phi \right )\right \vert.\\ \end{array} }$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equy.gif) The function H is the Heaviside function defined by H(x) = 1 if x ≥ 0, H(x) = 0 otherwise. In practice, we replace H by a smooth approximation
The function H is the Heaviside function defined by H(x) = 1 if x ≥ 0, H(x) = 0 otherwise. In practice, we replace H by a smooth approximation 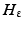 , e.g.,
, e.g.,
![$$\displaystyle{H_{\varepsilon }\left (x\right ) = \frac{1} {2}\left [1 + \frac{2} {\pi } \arctan \left (\frac{x} {\varepsilon } \right )\right ].}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equz.gif) Although this method makes splitting and merging of curves a simple matter, the energy functional is non-convex which possesses many local minima. These local minima may correspond to undesirable segmentations; see [45].
Although this method makes splitting and merging of curves a simple matter, the energy functional is non-convex which possesses many local minima. These local minima may correspond to undesirable segmentations; see [45].
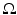 , the piecewise constant Mumford-Shah model seeks a set of curves C and a set of constant
, the piecewise constant Mumford-Shah model seeks a set of curves C and a set of constant  which minimize the energy functional given by
which minimize the energy functional given by![$$\displaystyle{ F^{MS}\left (C,\mathbf{c}\right ) =\sum \limits _{ l=1}^{L}\int _{ \Omega _{l}}\left [f\left ({\mathbf{x}}\right ) - c_{l}\right ]^{2}d{\mathbf{x}} +\beta \cdot \text{Length}\left (C\right ). }$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equx.gif)
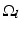 for
for 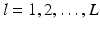 . The idea is to partition the image, so that the intensity of f in each segment
. The idea is to partition the image, so that the intensity of f in each segment 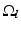 is well approximated by a constant c l . The goodness of fit is measured by the L 2 difference between f and c l . On the other hand, a minimum description length principle is employed which requires the curves C to be as short as possible. This increases the robustness to noise and avoids spurious segments. The parameter
is well approximated by a constant c l . The goodness of fit is measured by the L 2 difference between f and c l . On the other hand, a minimum description length principle is employed which requires the curves C to be as short as possible. This increases the robustness to noise and avoids spurious segments. The parameter 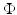 defined on the image domain. The objective function then becomes
defined on the image domain. The objective function then becomes![$$\displaystyle{\begin{array}{rl} F^{{\mathrm{CV}}}\left (\phi,c_{ 1},c_{2}\right )& =\int _{\Omega }H\left (\phi \left ({\mathbf{x}}\right )\right )\left [f\left ({\mathbf{x}}\right ) - c_{1}\right ]^{2}d{\mathbf{x}} \\ &\quad +\int _{\Omega }\left [1 - H\left (\phi \left ({\mathbf{x}}\right )\right )\right ]\left [f\left ({\mathbf{x}}\right ) - c_{2}\right ]^{2}d{\mathbf{x}} +\beta \int _{ \Omega }\left \vert \nabla H\left (\phi \right )\right \vert.\\ \end{array} }$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equy.gif)
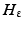 , e.g.,
, e.g.,![$$\displaystyle{H_{\varepsilon }\left (x\right ) = \frac{1} {2}\left [1 + \frac{2} {\pi } \arctan \left (\frac{x} {\varepsilon } \right )\right ].}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equz.gif)
Interestingly, for fixed c 1 and c 2, the above non-convex objective can be reformulated as a convex problem, so that a global minimum can be easily computed; see [22, 56]. The globalized objective is given by
![$$\displaystyle{ F^{{\mathrm{CEN}}}\left (u,c_{ 1},c_{2}\right ) =\int _{\Omega }\left \{\left [f\left ({\mathbf{x}}\right ) - c_{1}\right ]^{2} -\left [f\left ({\mathbf{x}}\right ) - c_{ 2}\right ]^{2}\right \}u\left ({\mathbf{x}}\right )d{\mathbf{x}} +\beta \int _{ \Omega }\left \vert \nabla u\right \vert }$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equ7.gif)
which is minimized over all u satisfying the bilateral constraints 0 ≤ u ≤ 1 and all scalars c 1 and c 2. After a solution u is obtained, a global solution to the original two-phase Mumford-Shah objective can be obtained by thresholding u with μ for almost every μ ∈ [0,1], see [22, 56]. Some other proposals for computing global solutions can be found in [45].
![$$\displaystyle{ F^{{\mathrm{CEN}}}\left (u,c_{ 1},c_{2}\right ) =\int _{\Omega }\left \{\left [f\left ({\mathbf{x}}\right ) - c_{1}\right ]^{2} -\left [f\left ({\mathbf{x}}\right ) - c_{ 2}\right ]^{2}\right \}u\left ({\mathbf{x}}\right )d{\mathbf{x}} +\beta \int _{ \Omega }\left \vert \nabla u\right \vert }$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equ7.gif)
(7)
To optimize the globalized objective function (7), Chan et al. [22] proposed to use an exact penalty method to convert the bilaterally constrained problem to an unconstrained problem. Then the gradient descent method is applied. This method is very robust and easy to implement. Moreover, the exact penalty method treats the constraints gracefully, as if there is no constraint at all. But of course the gradient descent is not particular fast.
In [42], Krishnan et al. considered the following discrete two-phase Mumford-Shah model:
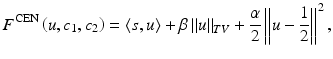 where
where 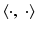 is the l 2 inner product, s = (s i, j ), and
is the l 2 inner product, s = (s i, j ), and
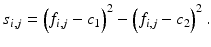 The variable u is bounded by the bilateral constraints 0 ≤ u ≤ 1. When
The variable u is bounded by the bilateral constraints 0 ≤ u ≤ 1. When 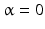 , this problem is convex but not strictly convex. When
, this problem is convex but not strictly convex. When 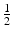 is introduced in the third term so that the minimizer does not bias toward u = 0 or u = 1. This problem is exactly a TV denoising problem with bound constraints. Krishnan et al. proposed to use the primal-dual active-set method to solve the problem. Superlinear convergence has been established.
is introduced in the third term so that the minimizer does not bias toward u = 0 or u = 1. This problem is exactly a TV denoising problem with bound constraints. Krishnan et al. proposed to use the primal-dual active-set method to solve the problem. Superlinear convergence has been established.
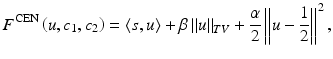
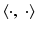 is the l 2 inner product, s = (s i, j ), and
is the l 2 inner product, s = (s i, j ), and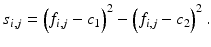
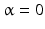 , this problem is convex but not strictly convex. When
, this problem is convex but not strictly convex. When 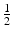 is introduced in the third term so that the minimizer does not bias toward u = 0 or u = 1. This problem is exactly a TV denoising problem with bound constraints. Krishnan et al. proposed to use the primal-dual active-set method to solve the problem. Superlinear convergence has been established.
is introduced in the third term so that the minimizer does not bias toward u = 0 or u = 1. This problem is exactly a TV denoising problem with bound constraints. Krishnan et al. proposed to use the primal-dual active-set method to solve the problem. Superlinear convergence has been established.Diffusion Tensors Images
Recently, diffusion tensor imaging (DTI), a kind of magnetic resonance (MR) modality, becomes increasingly popular. It enables the study of anatomical structures such as nerve fibers in human brains noninvasively. Moreover, the use of direction-sensitive acquisitions results in its lower signal-to-noise ratio compared to convectional MR. At each voxel in the imaging domain, the anisotropy of diffusion water molecules is interested. Such an anisotropy can be described by a diffusion tensor D, which is a 3 × 3 positive semi-definite matrix. By standard spectral theory results, D can be factorized into
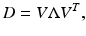 where V is an orthogonal matrix whose columns are the eigenvectors of D, and Λ is a diagonal matrix whose diagonal entries are the corresponding eigenvalues. These eigenvalues provide the diffusion rate along the three orthogonal directions defined by the eigenvectors. The goal is to estimate the matrix D (one at each voxel) from the data. Under the Stejskal-Tanner model, the measurement S k from the imaging device and the diffusion tensor are related by
where V is an orthogonal matrix whose columns are the eigenvectors of D, and Λ is a diagonal matrix whose diagonal entries are the corresponding eigenvalues. These eigenvalues provide the diffusion rate along the three orthogonal directions defined by the eigenvectors. The goal is to estimate the matrix D (one at each voxel) from the data. Under the Stejskal-Tanner model, the measurement S k from the imaging device and the diffusion tensor are related by
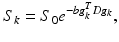
where S 0 is the baseline measurement, g k is the prescribed direction in which the measurement is done, and b > 0 is a scalar depending the strength of the magnetic field applied and the acquisition time. Since D has six degrees of freedom, six measurements at different orientations are needed to reconstruct D. In practice, the measurements are very noisy. Thus, matrix D obtained by directly solving (8) for 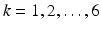 may not be positive semi-definite and is error-prone. It is thus often helpful to take more than six measurements and to use some least squares methods or regularization to obtain a robust estimate while preserving the positive semi-definiteness for physical correctness.
may not be positive semi-definite and is error-prone. It is thus often helpful to take more than six measurements and to use some least squares methods or regularization to obtain a robust estimate while preserving the positive semi-definiteness for physical correctness.
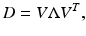
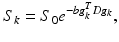
(8)
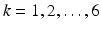 may not be positive semi-definite and is error-prone. It is thus often helpful to take more than six measurements and to use some least squares methods or regularization to obtain a robust estimate while preserving the positive semi-definiteness for physical correctness.
may not be positive semi-definite and is error-prone. It is thus often helpful to take more than six measurements and to use some least squares methods or regularization to obtain a robust estimate while preserving the positive semi-definiteness for physical correctness.In [60] Wang et al. and in [25] Christiansen et al. proposed an extension of the ROF to denoise tensor-valued data. Two major differences between the two works are that the former regularizes the Cholesky factor of D and uses a channel-by-channel TV regularization, whereas the latter regularizes the tensor D directly and uses a multichannel TV.
The method in [25] is two staged. The first stage is to estimate the diffusion tensors from the raw data based on the Stejskal-Tanner model (8). The obtained tensors are often noisy and may not be positive semi-definite. The next stage is to use the ROF model to denoise the tensor while restricting the results to be positive semi-definite. The trick they used to ensure positive semi-definiteness is very simple and practical. They observed that a symmetric matrix is positive semi-definite if and only if it has a Cholesky factorization of the form
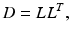 where L is a lower triangular matrix
where L is a lower triangular matrix
![$$\displaystyle{L = \left [\begin{array}{*{20}c} l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\ l_{31} & l_{32} & l_{33}\\ \end{array} \right ].}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equae.gif) Then one can easily express D in terms of l ij for
Then one can easily express D in terms of l ij for 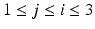 :
:
![$$\displaystyle{D = D\left (L\right ) = \left [\begin{array}{*{20}c} l_{11}^{2} & l_{11}l_{21} & l_{11}l_{31} \\ l_{11}l_{21} & l_{21}^{2} + l_{22}^{2} & l_{21}l_{31} + l_{22}l_{32} \\ l_{11}l_{31} & l_{21}l_{31} + l_{22}l_{32} & l_{31}^{2} + l_{32}^{2} + l_{33}^{2}\\ \end{array} \right ].}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equaf.gif) The ROF problem, written in a continuous domain, is then formulated as
The ROF problem, written in a continuous domain, is then formulated as
![$$\displaystyle{\mathop{\min }\limits _{L}\left \{\frac{1} {2}\sum \limits _{ij}\int _{\Omega }\left [d_{ij}\left (L\right ) -\hat{ d}_{ij}\right ]^{2}d{\mathbf{x}} +\lambda \sqrt{\sum \limits _{ ij}\left [\int _{\Omega }\left \vert \nabla d_{ij}\left (L\right )\right \vert \right ]^{2}}\right \},}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equag.gif) where
where 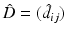 is the observed noisy tensor field, and L is the unknown lower triangular matrix-valued function from
is the observed noisy tensor field, and L is the unknown lower triangular matrix-valued function from 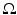 to
to 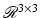 . Here, the matrix-valued version of TV is used. The objective is then differentiated w.r.t. the lower triangular part of L to obtain a system of six first-order optimality conditions. Once the optimal L is obtained, the tensor D can be formed by taking D = LL T which is a positive semi-definite.
. Here, the matrix-valued version of TV is used. The objective is then differentiated w.r.t. the lower triangular part of L to obtain a system of six first-order optimality conditions. Once the optimal L is obtained, the tensor D can be formed by taking D = LL T which is a positive semi-definite.
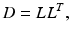
![$$\displaystyle{L = \left [\begin{array}{*{20}c} l_{11} & 0 & 0 \\ l_{21} & l_{22} & 0 \\ l_{31} & l_{32} & l_{33}\\ \end{array} \right ].}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equae.gif)
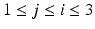 :
:![$$\displaystyle{D = D\left (L\right ) = \left [\begin{array}{*{20}c} l_{11}^{2} & l_{11}l_{21} & l_{11}l_{31} \\ l_{11}l_{21} & l_{21}^{2} + l_{22}^{2} & l_{21}l_{31} + l_{22}l_{32} \\ l_{11}l_{31} & l_{21}l_{31} + l_{22}l_{32} & l_{31}^{2} + l_{32}^{2} + l_{33}^{2}\\ \end{array} \right ].}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equaf.gif)
![$$\displaystyle{\mathop{\min }\limits _{L}\left \{\frac{1} {2}\sum \limits _{ij}\int _{\Omega }\left [d_{ij}\left (L\right ) -\hat{ d}_{ij}\right ]^{2}d{\mathbf{x}} +\lambda \sqrt{\sum \limits _{ ij}\left [\int _{\Omega }\left \vert \nabla d_{ij}\left (L\right )\right \vert \right ]^{2}}\right \},}$$](/wp-content/uploads/2016/04/A183156_2_En_24_Chapter_Equag.gif)
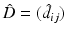 is the observed noisy tensor field, and L is the unknown lower triangular matrix-valued function from
is the observed noisy tensor field, and L is the unknown lower triangular matrix-valued function from 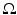 to
to 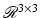 . Here, the matrix-valued version of TV is used. The objective is then differentiated w.r.t. the lower triangular part of L to obtain a system of six first-order optimality conditions. Once the optimal L is obtained, the tensor D can be formed by taking D = LL T which is a positive semi-definite.
. Here, the matrix-valued version of TV is used. The objective is then differentiated w.r.t. the lower triangular part of L to obtain a system of six first-order optimality conditions. Once the optimal L is obtained, the tensor D can be formed by taking D = LL T which is a positive semi-definite.The original ROF problem is strictly convex so that one can obtain the globally optimal solution. However, in this problem, due to the nonlinear change of variables from D to L, the problem becomes non-convex. But the authors of [25] reported that in their experiments, different initial data often resulted in the same solution, so that the non-convexity does not pose any significant difficulty to the optimization of the objective.
4 Numerical Methods and Case Examples
Fast numerical methods for TV minimization continue to be an active research area. Researchers from different fields have been bringing many fresh ideas to the problem and led to many exciting results. Some categories of particular mention are dual/primal-dual methods, Bregman iterative methods, and graph cut methods. Many of these methods have a long history with a great deal of general theories developed. But when it comes to their application to the ROF model, many further properties and specialized refinements can be exploited to obtain even faster methods. Having said so, different algorithms may adopt different versions of TV. They have different properties and thus may be used for different purposes. Thus, some caution needs to be taken when one attempts to draw conclusions such as method A is faster than method B. Moreover, different methods have different degree of generality. Some methods can be extended directly to deblurring, while some can only be applied to denoising. (Of course, one can use an outer iteration to solve a deblurring problem by a sequence of denoising problems, so that any denoising algorithm can be used. But the convergence of the outer iteration has little, if not none, to do with the inner denoising algorithm.) This section surveys some recent methods for TV denoising and/or deblurring. The model considered here is a generalized ROF model which simultaneously performs denoising and deblurring. The objective function reads
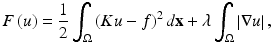
where K is a blurring operator and λ > 0 is the regularization parameter. For simplicity, we assume that K is invertible. When K is the identity operator, (9) is the ROF denoising model.
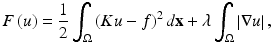
(9)
Dual and Primal-Dual Methods
The ROF objective is non-differentiable in flat regions where 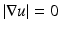 . This leads to much difficulty in the optimization process since gradient information (hence, Taylor’s expansion) becomes unreliable in predicting the function value even locally. Indeed, the staircase effects of TV minimization can introduce some flat regions which make the problem worse. Even if the standard procedure of replacing the TV with a reasonably smoothed version is used so that the objective becomes differentiable, the Euler-Lagrange equation for (9) is still very stiff to solve. Higher-order methods such as Newton’s methods often fail to work because higher-order derivatives are even less reliable.
. This leads to much difficulty in the optimization process since gradient information (hence, Taylor’s expansion) becomes unreliable in predicting the function value even locally. Indeed, the staircase effects of TV minimization can introduce some flat regions which make the problem worse. Even if the standard procedure of replacing the TV with a reasonably smoothed version is used so that the objective becomes differentiable, the Euler-Lagrange equation for (9) is still very stiff to solve. Higher-order methods such as Newton’s methods often fail to work because higher-order derivatives are even less reliable.
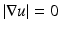 . This leads to much difficulty in the optimization process since gradient information (hence, Taylor’s expansion) becomes unreliable in predicting the function value even locally. Indeed, the staircase effects of TV minimization can introduce some flat regions which make the problem worse. Even if the standard procedure of replacing the TV with a reasonably smoothed version is used so that the objective becomes differentiable, the Euler-Lagrange equation for (9) is still very stiff to solve. Higher-order methods such as Newton’s methods often fail to work because higher-order derivatives are even less reliable.
. This leads to much difficulty in the optimization process since gradient information (hence, Taylor’s expansion) becomes unreliable in predicting the function value even locally. Indeed, the staircase effects of TV minimization can introduce some flat regions which make the problem worse. Even if the standard procedure of replacing the TV with a reasonably smoothed version is used so that the objective becomes differentiable, the Euler-Lagrange equation for (9) is still very stiff to solve. Higher-order methods such as Newton’s methods often fail to work because higher-order derivatives are even less reliable.Due to the difficulty in optimizing the ROF objective directly, much recent research has been directed toward solving some reformulated versions. In particular, methods based on dual and primal-dual formulations have been shown to be very fast in practice. Actually, the dual problem (see (12) below) also has its own numerical difficulties to face, e.g., the objective is rank deficient and some extra work is needed to deal with the constraints. But the dual formulation brings many well-developed ideas and techniques from numerical optimization to bear on this problem. Primal-dual methods have also been studied to combine information from the primal and dual solutions. Several successful dual and primal-dual methods are reviewed.
Chan-Golub-Mulet’s Primal-Dual Method
Some early work in dual and primal-dual methods for the ROF model can be found in [13, 20]. In particular, Chan, Golub, and Mulet (CGM) [20] introduced a primal-dual system involving a primal variable u




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



