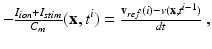Fig. 1.
Dimensional reduction of the AP manifold generated by the CRN model. The first six PCA modes are plotted.
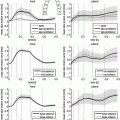
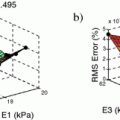
The topic of reduced-order modeling for cardiac electrophysiology has been explored in the literature. Most relevant to this work, an approach based on a Galerkin method for the solution of the bidomain equations, combined with proper orthogonal decomposition, has recently been proposed in [3]. Motivated by recent progresses in meta-modeling [9], we apply a data-driven approach to the reduction of state-of-the-art cellular models used for atria simulation in literature. The reduced model learned by regression keeps the ability to capture the complex dynamics of the original biophysically detailed model, while in simple form and depending on a smaller number of parameters. This makes the model efficient and suitable for use for large scale simulations at the organ level. To the best of our knowledge, this represents the first example of application of a model reduction technique based on statistical learning to the multiscale modeling of cardiac EP. In this work, we focus on the CRN atrial cell model. We first use the principal component analysis (PCA) to reduce the dimensionality of the AP manifold (Sect. 2.1). We then learn a regression model of AP dynamics at the cell level, given a set of CRN model parameters (Sect. 2.2). Finally we use this reduced cellular model for tissue-level EP modeling (Sect. 2.3). As reported in Sect. 3, AP manifold dimension can be reduced to 15 despite being the output of a non-linear system. Our regression model demonstrates the ability of capturing the physiological complexity of cardiac AP, and it drastically improves the performance of atrial tissue-level electrophysiology modeling by achieving a 75 % reduction of the computational cost with the same computational time step and two order of magnitudes smaller computational time with larger time steps (in the order of seconds to compute one heart cycle of electrical activation in a patient-specific atrial anatomy, using a regular workstation).
2 Methods
Although the methods described in the following do not depend on the specific choice of the cellular model, we focus here on a model suitable for the description of atrial electrophysiology. The CRN cell model was developed based on human atrial cell data and has been validated for use in both tissue [2] and organ [1] level simulations. The dominating equation is
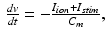
where 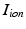 is the total current flowing through 12 ion channels,
is the total current flowing through 12 ion channels,  is a transient stimulus current added to simulate electrical pacing, and
is a transient stimulus current added to simulate electrical pacing, and 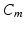 is the membrane capacitance per unit volume.
is the membrane capacitance per unit volume.
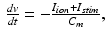
(1)
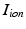 is the total current flowing through 12 ion channels,
is the total current flowing through 12 ion channels,  is a transient stimulus current added to simulate electrical pacing, and
is a transient stimulus current added to simulate electrical pacing, and 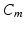 is the membrane capacitance per unit volume.
is the membrane capacitance per unit volume.For modeling electrophysiology at the tissue level, we resort to the monodomain model coupled with the CRN cell model. The model equation has the form
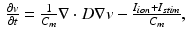
where v is the transmembrane potential, 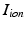 is the ionic current from the coupled cell model, and D is the anisotropic diffusion tensor.
is the ionic current from the coupled cell model, and D is the anisotropic diffusion tensor.
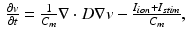
(2)
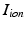 is the ionic current from the coupled cell model, and D is the anisotropic diffusion tensor.
is the ionic current from the coupled cell model, and D is the anisotropic diffusion tensor.2.1 AP Manifold Learning for Dimensionality Reduction
The solution of Eq. (1) is the time-dependent transmembrane action potential (AP) v(t). We use manifold learning techniques to reduce the dimensionality of the manifold 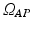 to which v(t) belongs. That is, we analyze the number of intrinsic parameters q that are necessary to capture the observed AP data v(t). Let n be the number of observations. For each observation i, we choose a unique set of model parameters
to which v(t) belongs. That is, we analyze the number of intrinsic parameters q that are necessary to capture the observed AP data v(t). Let n be the number of observations. For each observation i, we choose a unique set of model parameters 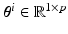 and compute the AP in m time snapshots. The results are gathered in the observation vector
and compute the AP in m time snapshots. The results are gathered in the observation vector ![$$\mathbf {v}^i = [v^i(t_1), \cdots , v^i(t_m)]\in \mathbb {R}^{1\times m}$$](/wp-content/uploads/2016/09/A339585_1_En_53_Chapter_IEq7.gif) . The
. The 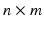 observation matrix
observation matrix ![$$\mathbf {Y} = [(\mathbf {v}^1)^T, \cdots , (\mathbf {v}^n)^T]^T$$](/wp-content/uploads/2016/09/A339585_1_En_53_Chapter_IEq9.gif) represents a sampling of the AP manifold. Before dimension reduction, the AP matrix is zscored. To uncover the intrinsic structure of the AP manifold, we adopt the principal component analysis (PCA) [7].
represents a sampling of the AP manifold. Before dimension reduction, the AP matrix is zscored. To uncover the intrinsic structure of the AP manifold, we adopt the principal component analysis (PCA) [7].
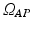 to which v(t) belongs. That is, we analyze the number of intrinsic parameters q that are necessary to capture the observed AP data v(t). Let n be the number of observations. For each observation i, we choose a unique set of model parameters
to which v(t) belongs. That is, we analyze the number of intrinsic parameters q that are necessary to capture the observed AP data v(t). Let n be the number of observations. For each observation i, we choose a unique set of model parameters 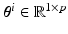 and compute the AP in m time snapshots. The results are gathered in the observation vector
and compute the AP in m time snapshots. The results are gathered in the observation vector ![$$\mathbf {v}^i = [v^i(t_1), \cdots , v^i(t_m)]\in \mathbb {R}^{1\times m}$$](/wp-content/uploads/2016/09/A339585_1_En_53_Chapter_IEq7.gif) . The
. The 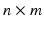 observation matrix
observation matrix ![$$\mathbf {Y} = [(\mathbf {v}^1)^T, \cdots , (\mathbf {v}^n)^T]^T$$](/wp-content/uploads/2016/09/A339585_1_En_53_Chapter_IEq9.gif) represents a sampling of the AP manifold. Before dimension reduction, the AP matrix is zscored. To uncover the intrinsic structure of the AP manifold, we adopt the principal component analysis (PCA) [7].
represents a sampling of the AP manifold. Before dimension reduction, the AP matrix is zscored. To uncover the intrinsic structure of the AP manifold, we adopt the principal component analysis (PCA) [7].2.2 Regression Model
We then learn a regression model of action potential dynamics given a sample space of the CRN model parameters 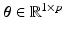 and their corresponding AP outputs
and their corresponding AP outputs 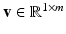 .
.
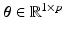 and their corresponding AP outputs
and their corresponding AP outputs 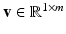 .
.Model Input. The CRN model parameters 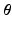 are the regression inputs.
are the regression inputs.
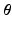 are the regression inputs.
are the regression inputs.Model Output. Instead of the time-series of action potential v(t), we consider the reduced AP representation computed in Sect. 2.1 as output: the regression model predicts the q embedding coordinates 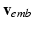 , which are then used to reconstruct the AP time frames
, which are then used to reconstruct the AP time frames 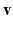 with the basis provided by PCA.
with the basis provided by PCA.
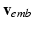 , which are then used to reconstruct the AP time frames
, which are then used to reconstruct the AP time frames 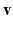 with the basis provided by PCA.
with the basis provided by PCA.Model Construction. The data-driven model writes 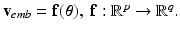 Rather than directly regressing
Rather than directly regressing 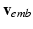 from
from 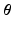 , we propose a two-step model construction process based on statistical learning. We first regress some phenomenological features of the AP, and then use them as additional inputs for the second regression step to increase the accuracy of the overall prediction. The rationale behind this choice is that many phenomenological features of AP can be regressed with high accuracy from
, we propose a two-step model construction process based on statistical learning. We first regress some phenomenological features of the AP, and then use them as additional inputs for the second regression step to increase the accuracy of the overall prediction. The rationale behind this choice is that many phenomenological features of AP can be regressed with high accuracy from 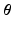 , as shown in Sect. 3, and adding them as features helps further constraining the second regression problem.
, as shown in Sect. 3, and adding them as features helps further constraining the second regression problem.
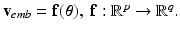 Rather than directly regressing
Rather than directly regressing 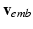 from
from 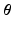 , we propose a two-step model construction process based on statistical learning. We first regress some phenomenological features of the AP, and then use them as additional inputs for the second regression step to increase the accuracy of the overall prediction. The rationale behind this choice is that many phenomenological features of AP can be regressed with high accuracy from
, we propose a two-step model construction process based on statistical learning. We first regress some phenomenological features of the AP, and then use them as additional inputs for the second regression step to increase the accuracy of the overall prediction. The rationale behind this choice is that many phenomenological features of AP can be regressed with high accuracy from 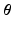 , as shown in Sect. 3, and adding them as features helps further constraining the second regression problem.
, as shown in Sect. 3, and adding them as features helps further constraining the second regression problem.More precisely, we characterize the action potential by different properties: peak voltage (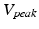 ), resting membrane potential (
), resting membrane potential ( ), action potential duration (APD). We learn a prediction model for these quantities
), action potential duration (APD). We learn a prediction model for these quantities ![$$\mathbf {f}_1:\varvec{\theta } \mapsto [V_{peak}, V_{rest}, APD]$$](/wp-content/uploads/2016/09/A339585_1_En_53_Chapter_IEq21.gif) using the projection pursuit regression (PPR) method [6]. In this work, we use the R function ppr. The second step of the full statistical learning procedure is to regress the embedding coordinates
using the projection pursuit regression (PPR) method [6]. In this work, we use the R function ppr. The second step of the full statistical learning procedure is to regress the embedding coordinates 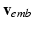 by including predicted values of those AP quantities as inputs together with the CRN model parameters
by including predicted values of those AP quantities as inputs together with the CRN model parameters 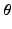 . This step estimates a model
. This step estimates a model ![$$\mathbf {f}_2:[\varvec{\theta }, \mathbf {f}_1(\varvec{\theta })] \mapsto \mathbf {v}_{emb}$$](/wp-content/uploads/2016/09/A339585_1_En_53_Chapter_IEq24.gif) using the PPR method as in the first step.
using the PPR method as in the first step.
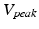 ), resting membrane potential (
), resting membrane potential ( ), action potential duration (APD). We learn a prediction model for these quantities
), action potential duration (APD). We learn a prediction model for these quantities ![$$\mathbf {f}_1:\varvec{\theta } \mapsto [V_{peak}, V_{rest}, APD]$$](/wp-content/uploads/2016/09/A339585_1_En_53_Chapter_IEq21.gif) using the projection pursuit regression (PPR) method [6]. In this work, we use the R function ppr. The second step of the full statistical learning procedure is to regress the embedding coordinates
using the projection pursuit regression (PPR) method [6]. In this work, we use the R function ppr. The second step of the full statistical learning procedure is to regress the embedding coordinates 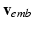 by including predicted values of those AP quantities as inputs together with the CRN model parameters
by including predicted values of those AP quantities as inputs together with the CRN model parameters 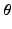 . This step estimates a model
. This step estimates a model ![$$\mathbf {f}_2:[\varvec{\theta }, \mathbf {f}_1(\varvec{\theta })] \mapsto \mathbf {v}_{emb}$$](/wp-content/uploads/2016/09/A339585_1_En_53_Chapter_IEq24.gif) using the PPR method as in the first step.
using the PPR method as in the first step.AP Prediction. Given a new set of parameters 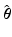 , the AP prediction is as follows
, the AP prediction is as follows
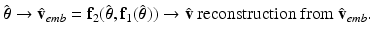
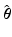 , the AP prediction is as follows
, the AP prediction is as follows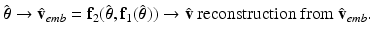
2.3 Application to Tissue-Level Atrial EP Modeling
We present a framework for efficient patient-specific simulation of cardiac transmembrane potential.
Computational Domain Preparation from Medical Images. Starting from atria images (e.g., from CT), the left and right atrium are automatically segmented using a machine learning approach [15]. Regional atrial wall thickness can be extracted from high resolution images, but this may be challenging to obtain for the whole atria. We follow a simpler approach, applying a uniform mesh thickening based on thresholding a level-set representation of the atrial surface on an isotropic Cartesian grid. Grid nodes lying at the sino-atrial node region are manually annotated. If available, information on the fibers orientation can be readily included in the computational domain, as described in [14] for the case of ventricular tissue. In this work we do not model the presence of fibers in the atrial tissue. Since tissue anisotropy plays a role in the monodomain equation, but not in the cell model, the proposed model reduction strategy is not affected by this choice.
Lattice-Boltzmann Method for Cardiac EP. We solve the monodomain tissue model on a Cartesian grid by applying the Lattice-Boltzmann method introduced in [11] to the discretization of the model equation. The method uses a 7-connectivity topology (6 connections + central position) and Neumann boundary conditions.
Registration of the Regression Cellular Model. The regression model we designed is discrete. Given a set of model parameters, the regression model predicts the full time sequence  of AP, in m time snapshots (as for the observations in the training data set). To obtain the potential value at each time in the heart cycle, we align
of AP, in m time snapshots (as for the observations in the training data set). To obtain the potential value at each time in the heart cycle, we align 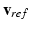 at the time
at the time  of AP upstroke or depolarization; then we extract the proper snapshot from
of AP upstroke or depolarization; then we extract the proper snapshot from 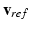 . To monitor
. To monitor  in each cell, we propose to use the simple Mitchell-Schaeffer (MS) model [10] (having only one gating variable). For the sake of clarity, we assume that the time step dt used by the monodomain solver is a multiple of the time step used to sample
in each cell, we propose to use the simple Mitchell-Schaeffer (MS) model [10] (having only one gating variable). For the sake of clarity, we assume that the time step dt used by the monodomain solver is a multiple of the time step used to sample 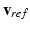 . After the upstroke, at time
. After the upstroke, at time  , the last term in Eq. (2) is computed as follows
, the last term in Eq. (2) is computed as follows
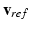 of AP, in m time snapshots (as for the observations in the training data set). To obtain the potential value at each time in the heart cycle, we align
of AP, in m time snapshots (as for the observations in the training data set). To obtain the potential value at each time in the heart cycle, we align 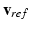 at the time
at the time  of AP upstroke or depolarization; then we extract the proper snapshot from
of AP upstroke or depolarization; then we extract the proper snapshot from 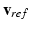 . To monitor
. To monitor  in each cell, we propose to use the simple Mitchell-Schaeffer (MS) model [10] (having only one gating variable). For the sake of clarity, we assume that the time step dt used by the monodomain solver is a multiple of the time step used to sample
in each cell, we propose to use the simple Mitchell-Schaeffer (MS) model [10] (having only one gating variable). For the sake of clarity, we assume that the time step dt used by the monodomain solver is a multiple of the time step used to sample 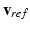 . After the upstroke, at time
. After the upstroke, at time  , the last term in Eq. (2) is computed as follows
, the last term in Eq. (2) is computed as follows