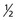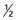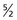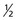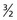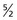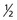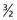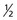Nuclear Magnetism
Objectives
At the completion of this chapter, the student should be able to do the following:
• Distinguish between classical mechanics and quantum mechanics.
• State the Larmor equation and relate its importance to magnetic resonance imaging (MRI).
• Describe the appearance of net magnetization on a vector diagram.
• Discuss the factors that influence the magnitude of net magnetization.
• Distinguish between stationary frame and rotating frame and state which is used in MRI.
Key Terms
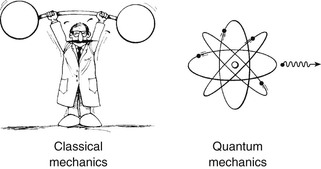
As the name nuclear magnetic resonance (NMR) indicates, the magnetic resonance imaging (MRI) signal originates from the nuclei of atoms resonating in a patient in the presence of a magnetic field. Because this is a nuclear phenomenon, an accurate and complete description requires the use of quantum mechanics.
Quantum mechanics is the branch of physics that describes the behavior of very small objects, such as x-rays, protons, neutrons, and electrons. This branch of physics evolved in the first quarter of the twentieth century and is the basis for contemporary investigations into the structure of matter. Quantum mechanics, though, is complex and does not provide an intuitive understanding of what is really happening during an MRI examination at the subatomic level.
Fortunately, many of the concepts that relate to how MR images are formed relate to net magnetizations that represent the summed properties of billions and billions of nuclear magnets, say in a drop of water. Therefore, we can think of the nuclear magnetization, as it is manifested in the cellular water of a patient, as being largely described by the principles of classical mechanics.
Classical mechanics deals with large objects; quantum mechanics deals with subatomic particles and photons.
Classical mechanics is the branch of physics that describes the behavior of large objects such as rockets, automobiles, and Ping-Pong balls. It has its origins in the seventeenth-century ideas of Sir Isaac Newton.
The differences between these two branches of physics are demonstrated in Figure 3-1. For many cases, the statistical averaging that occurs over a patient reduces the quantum mechanical description to a classical mechanical description. One quantum mechanical concept, however, that cannot be overlooked or avoided is nuclear spin.
Quantum Mechanical Description
According to quantum mechanics, every nucleus has a quantity called spin. This quantity is not exactly what is normally thought of as spin, but it is close enough.
There is one anomaly, though; this spin is quantized into units of half-integer values and called the spin quantum number. There are only certain precisely allowed states of spin. The allowed values are 0,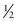 
, 1,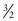 
, and so on.
Each nucleus has its own characteristic spin quantum number. For example, all hydrogen atoms of atomic mass 1 have a spin quantum number of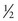 
. All carbon atoms of atomic mass 12 have a spin quantum number of 0. All carbon atoms of atomic mass 13 have a spin quantum number of 
.
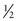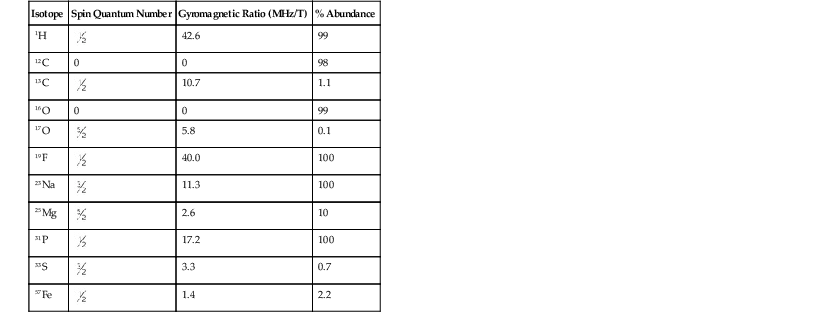
The spin quantum number dictates many of the magnetic resonance (MR) properties of a given nuclear species. Table 3-1 presents some nuclei of interest to MRI and their respective spin quantum numbers. Once this quantum mechanical premise is accepted, it is easy to use classical mechanics to describe the way the MR signal is generated.
One result of the spin being quantized is that there are a limited number of ways a nucleus can spin. Each of these ways is called a spin state. For a spin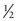 
nucleus, there are only two allowed spin states, 
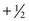and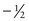 
.
In general, for a particle with spin S, there are 2S possible spin states, and each spin state is one integer value separated from the next. Thus for a nucleus such as 23Na with a spin quantum number of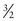 
, the allowed spin states are 
, 
, 
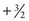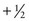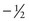, and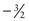 
.
A fundamental law of physics states that a spinning, charged mass induces a magnetic field about itself. Earth is one such example. The nucleus is a spinning, charged particle and therefore has an associated magnetic field. This field is given the special name of nuclear magnetic moment, and its intensity is related to the mass, charge, and rate of spin of the nucleus.
A spinning proton induces nuclear magnetism.
Thus each spin state has a different nuclear magnetic moment. In the absence of an external magnetic field, each spin state has the same energy, but in the presence of an external magnetic field, each spin state has a different energy and this energy difference increases as the external magnetic field increases.
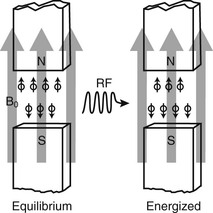
A nucleus in the presence of an external magnetic field prefers to be in the lower energy state rather than in the higher energy state. Therefore the lower energy state has more nuclei than the higher energy state. Such a system of nuclear spins is said to be at equilibrium with the external magnetic field.
With the use of electromagnetic radiation that has an energy exactly equal to the energy difference between two nuclear energy states, this population difference can be disturbed by causing some nuclei of a lower energy state to absorb energy and join the higher energy nuclei (Figure 3-2). The system of energized nuclear spins slowly returns to its original population difference while emitting a signal that can be observed. This is the MRI signal.
Classical Mechanical Description
From the classical mechanics point of view, the nucleus is simply a charged particle that is spinning. The spinning motion generates a magnetic field parallel to the axis of spin.
This magnetic field is given the same name of nuclear magnetic moment (µ) that was described in quantum mechanics (Figure 3-3). It is referred to with the Greek letter mu (µ). For any individual nucleus, the orientation of the axis of rotation and therefore the direction of the nuclear magnetic moment is random.
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
