Nuclear Medicine: Fundamentals

Bruce Mahoney, MD

Vineeth Yeluru, MBBS

LEARNING OBJECTIVES

1. Define the terms radioactivity, radionuclide, and radiopharmaceutical.
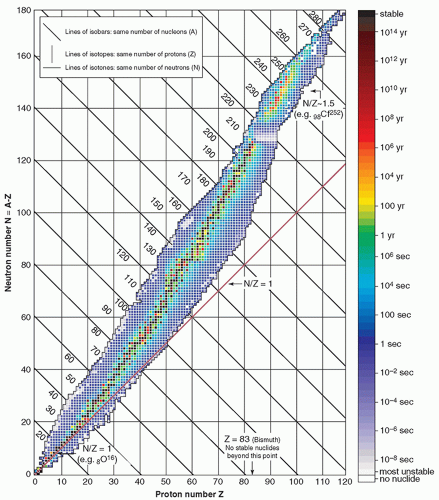
2. Explain the structural difference between radioisotopes and stable isotopes.
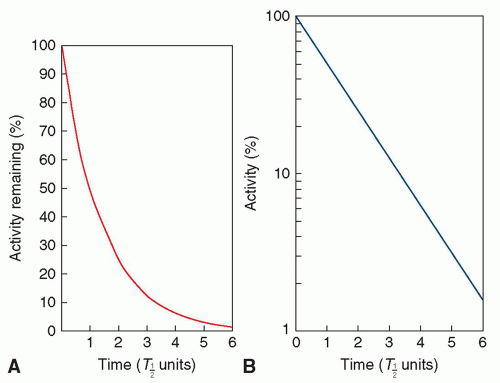
3. Define the terms activity, radioactive decay, and physical half-life.
4. Name five modes of radioactive decay. For each mode, name the nuclear deficiency of the parent, the common emissions, and an example radionuclide.
5. Describe the function of a radionuclide reactor. State the most common nuclear deficiency of reactor-produced radionuclides and their decay mode. Provide examples of two reactor-produced radionuclides.
6. Describe the function of a cyclotron. State the most common nuclear deficiency of cyclotron-produced radionuclides and their decay mode. Provide examples of two cyclotron-produced radionuclides.
7. Describe the function of a radionuclide generator. Define the terms transient equilibrium and secular equilibrium. Provide examples of two generator-produced radionuclides.
8. Name five mechanisms of radiopharmaceutical localization and provide an example radiopharmaceutical for each.
9. Describe the effects of half-life and gamma photon energy on patient radiation dose.
10. Define the terms deterministic effect and stochastic effect.
11. Describe a scenario leading to a medical event, and the reporting requirements in a Non-Agreement State.

INTRODUCTION

Nuclear medicine is a medical specialty that employs radioisotopes in the diagnosis and treatment of disease. A radioisotope is an unstable atomic species that can undergo nuclear transformation, releasing radiation. The term radionuclide refers specifically to the unstable atomic nucleus, although is often used interchangeably with radioisotope. Some of the forms of radiation released can be used for imaging, quantitative measurement, and radiation therapy. A radiopharmaceutical is a radioisotope or radiolabeled molecule able to localize within the body. Refer to Chapter 1 for a review of atomic structure and terminology.

Atomic nuclei are composed of protons and neutrons held together by the strong nuclear force. The repulsive force of the positively charged protons must be overcome by the strong force for nuclei to be stable. This stability occurs when there is an ideal ratio of neutrons and protons (the N/Z ratio) (Figure 8.1). This ideal ratio is approximately 1:1 for smaller nuclides, and approaches 1.5:1 for heavy nuclides. Nuclei with too many neutrons fall above the line and are termed proton deficient. Those with too few neutrons, falling below the line, are said to be neutron deficient. Both proton-deficient and neutron-deficient radionuclides can undergo nuclear transformation to bring their N/Z ratio toward greater stability. Radioactivity is the release of particles and photons by radionuclides during these nuclear transformations.

Unlike most other imaging modalities in medicine, nuclear medicine imaging generally focuses on depicting normal physiology and disturbances of function. Gamma rays and X-rays produced during nuclear transformation can be detected for image creation as well as for quantification. The resolutions of planar gamma camera imaging, single-photon emission computed tomography (SPECT) and positron emission tomography (PET) are lower than that of X-ray computed tomography (CT) and magnetic resonance imaging (MRI) by an order of magnitude or more (Figure 8.2). Radiopharmaceuticals localize to tissues or compartments on the basis of various mechanisms (see Section “Mechanisms of Radiopharmaceutical Localization” later), and therefore nuclear imaging does not illustrate the full spectrum of anatomy within a region of interest. This corresponding anatomic information can be provided by combining nuclear imaging data with anatomic imaging data, such as CT. Such hybrid imaging allows
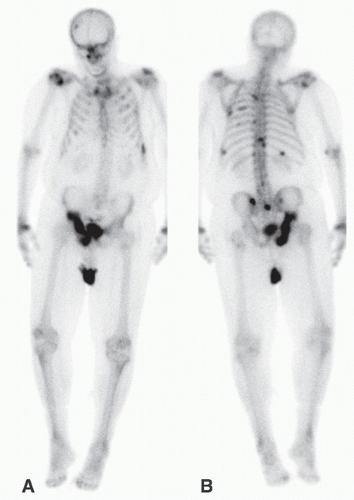
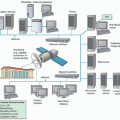
for increased diagnostic accuracy of nuclear imaging. SPECT/CT, PET/CT, and PET/MRI are powerful hybrid imaging tools.

FIG. 8.1 • A plot of the nuclides where the number of protons (ie, atomic number or Z) and neutrons of each nuclide is shown on the x– and y-axes, respectively. The stable nuclides form the so-called line of stability in which the neutron-to-proton ratio is approximately 1 for low Z nuclides and increases to approximately 1.5 for high Z nuclides. Note that all nuclides with Z >83 (bismuth) are radioactive and that, in general, the further the radionuclide is from the line of stability, the more unstable it is and the shorter the half-life it has. Radionuclides to the left of the line of stability are neutron rich and are likely to undergo beta-minus decay, whereas radionuclides to the right of the line of stability are neutron poor and thus often decay by positron emission or electron capture. Extremely unstable radionuclides and those with high Z often decay by alpha particle emission. Reprinted with permission from Bushberg JT, Seibert JA, Leidholdt EM, Boone JM. Essential Physics of Medical Imaging. 3rd ed. Philadelphia, PA: Wolters Kluwer Health/Lippincott Williams & Wilkins; 2012.

RADIOACTIVITY

Radioactive material (RAM) contains atoms undergoing radioactive decay. Each individual unstable nucleus has a likelihood of undergoing nuclear transformation in a given span of time that is based on its stability. Each decay event appears to be random and unaffected by outside events. However, a sample containing a large number of unstable nuclei will appear to emit radiation continuously at a rate that declines steadily. This rate is known as the activity of the sample.

The radioactivity of a sample is proportional to the number of unstable nuclei present. Thus, a quantity of RAM may be expressed in terms of its activity A, which refers to the number of nuclear transformations per unit time. The International System of Units (SI) unit of activity is the bequerel (Bq), which is defined
as an activity of 1 disintegration per second (dps). The curie (Ci), named after radioactivity pioneers Pierre and Marie Curie, is the traditional unit of activity equal to 3.70 × 10¹⁰ dps. Thus,

FIG. 8.2 • (A) Anterior and (B) posterior views from a whole-body 99mTc methylene diphosphonate (MDP) bone scan in a patient with prostate cancer. Focal areas of increased MDP uptake in the ribs, spine, sacrum, and pelvis are due to metastatic prostate cancer. Uptake in the wrists and right shoulder is related to arthritis. Excreted activity is present in the bladder and there is a small amount of contamination more inferiorly. A focus of uptake in the right skull corresponds with the site of a ventriculoperitoneal shunt.

1 Ci = 3.7 × 10¹⁰ Bq = 37 GBq

and

1 mCi = 37 MBq

Within the context of nuclear medicine, 1 Curie represents a large amount of radioactivity. The activity of most dosages of radiopharmaceuticals used in clinical nuclear medicine are measured in millicuries or microcuries (megabequerels). Despite the wide adoption of SI, traditional units such as the curie and millicurie are also still used in many countries, including in the United States.

Decay Constant and Physical Half-Life

The activity A of a sample of RAM is proportional to the number of available unstable nuclei in the sample, N. The decay constant λ relates activity with N

A = λ N

Ongoing nuclear disintegrations reduce the number of available unstable nuclei over time, with a corresponding decrease in activity A. A decreases over time as an exponential decay function known as the fundamental decay equation:

A_t = A₀e^-λt

where A₀ is the original activity and A_t is the activity at time t.

The length of time for the number of radioactive atoms (N) and the activity of the sample (A) to decrease by half is a constant known as the physical half-life T_p½. Physical half-life is inversely proportional to the decay constant

T_p½ = 0.693/λ

λ and T_p½ are properties unique to each radionuclide.

Physical half-life is an intuitive and useful concept. It is more convenient than applying the fundamental decay equation for calculating or quickly estimating the remaining activity in a sample following the passage of time. With each half-life, the activity of a sample decreases by half. After n half-lives have elapsed, activity A is given by the equation

A = A₀/2ⁿ

where A₀ is the original activity.

Examples:

^99mTc has a physical half-life of 6.02 hours. Approximately how much of a sample of ^99mTc remains after 24 hours?
- 24 hours represents almost four half-lives.
- A = A₀/2⁽⁴⁾ = A₀/16.
- Approximately 1/16th of the original activity remains after 24 hours.
If 20 mCi of ^99mTc sestamibi is administered to a patient, how much activity remains after 24 hours, assuming no physiologic clearance?
- 20 mCi/16 = 1.26 mCi
As a rule of thumb, a radioactive sample will decay to approximately 1/1000th its original activity after 10 half-lives (2¹⁰ = 1024). How long will it take a sample of ^99mTc to decay to 1/1000th of its original activity?
- For ^99mTc, 10 half-lives is approximately 60 hours, or 2½ days.
At 8 PM on Friday evening, a 100 mCi vial of ^99mTc pertechnetate is spilled on a carpeted surface in the nuclear medicine department, completely soaks in, and cannot be removed. How much activity remains when the first patient shows up at 8 AM Monday morning, 2½ days later? (Figure 8.3).
- 100 mCi/1000 = 0.1 mCi = 100 µCi

FIG. 8.3 • Percentage of initial activity as a function of time. A. Plot on linear graph. B. Plot on semilogarithmic graph. Reprinted with permission from Bushberg JT, Seibert JA, Leidholdt EM, Boone JM. Essential Physics of Medical Imaging. 3rd ed. Philadelphia, PA: Wolters Kluwer Health/Lippincott Williams & Wilkins; 2012.

Table 8.1 PHYSICAL HALF-LIFE (T_p½) AND DECAY CONSTANT (λ) FOR RADIONUCLIDES USED IN NUCLEAR MEDICINE

Radionuclide	T_p½	λ
Rubidium-82 (⁸²Rb)	75 s	0.0092 s^-1
Fluorine-18 (¹⁸F)	110 min	0.0063 min^-1
Technetium-99m (^99mTc)	6.02 h	0.1151 h^-1
Iodine-123 (¹²³I)	13.27 h	0.0522 h^-1
Samarium-153 (¹⁵³Sm)	1.93 d	0.3591 d^-1
Yttrium-90 (⁹⁰Y)	2.69 d	0.2575 d^-1
Molybdenum-99 (⁹⁹Mo)	2.75 d	0.2522 d^-1
Indium-111 (¹¹¹In)	2.81 d	0.2466 d^-1
Thallium-201 (²⁰¹Tl)	3.04 d	0.2281 d^-1
Gallium-67 (⁶⁷Ga)	3.26 d	0.2126 d^-1
Xenon-133 (¹³³Xe)	5.24 d	0.1323 d^-1
Iodine-131 (¹³¹I)	8.02 d	0.0864 d^-1
Phosphorus-32 (³²P)	14.26 d	0.0486 d^-1
Strontium-82 (⁸²Sr)	25.60 d	0.0271 d^-1
Chromium-51 (⁵¹Cr)	27.70 d	0.0250 d^-1
Strontium-89 (⁸⁹Sr)	50.53 d	0.0137 d^-1
Iodine-125 (¹²⁵I)	59.41 d	0.0117 d^-1
Cobalt-57 (⁵⁷Co)	271.79 d	0.0025 d^-1
Reprinted with permission from Bushberg JT, Seibert JA, Leidholdt EM, Boone JM. Essential Physics of Medical Imaging. 3rd ed. Philadelphia, PA: Wolters Kluwer Health/Lippincott Williams & Wilkins; 2012.

The half-lives of most radionuclides used for clinical nuclear imaging are measured in hours. Rubidium-82 (Rb-82), used in myocardial perfusion PET imaging, has a relatively short half-life of 1 minute 15 seconds. To perform PET imaging with Rb-82, it is necessary to have an on-site strontium-82/rubidium-82 (Sr-82/Rb-82) generator. In contrast, fluorine-18 (F-18) has a half-life of nearly 2 hours, allowing for a central facility to produce doses and distribute them regionally. Reusable sources for determining gamma camera image uniformity employ Cobalt-57, which has a half-life of approximately 9 months (Table 8.1).

Table 8.2 RADIOACTIVE DECAY MODES FOR UNSTABLE NUCLEI CONTAINING PROTONS (Z), NEUTRONS (N), AND MASS NUMBER (A)

	Daughter Nucleus Value
Decay Mode	Mass Number	Atomic Number	Neutron Number	Comments
Isomeric transition	A	Z	N	Metastable if half-life is long
Beta minus (β^–)	A	Z + 1	N − 1	Nucleus emits electrons
Beta plus (β⁺)	A	Z − 1	N + 1	Nucleus emits positrons
Electron capture	A	Z − 1	N + 1	Atoms emit characteristic X-rays^a
Alpha decay	A – 4	Z − 2	N − 2	Occurs with heavy nuclei (Z > 82)
^aWhen inner shell vacancies are filled.
Reprinted with permission from Huda W. Review of Radiologic Physics. 4th ed. Philadelphia, PA: Wolters Kluwer; 2016.

Modes of Decay

Unstable isotopes undergo radioactive decay by one or more of several mechanisms. The parent nuclide undergoes decay, producing one or more daughter species, which may be stable and/or radioactive (Table 8.2).

Isotopes which are proton deficient seek to increase their atomic number for greater stability. One example is phosphorus-32 (P-32). The stable isotope of phosphorus is phosphorus-31 (P-31), with 15 protons and 16 neutrons. Radioisotope P-32 has a higher atomic weight because of having an extra neutron compared with P-31 (high N/Z). This extra neutron results in its instability.

β^– decay

In beta-minus decay (β^– decay, negatron decay, beta emission), the nucleus emits a beta particle β^–, which is an electron, as well as an antineutrino [v with bar above], allowing a proton-deficient radioisotope to reduce its N/Z ratio.

^A_ZX → ^A_{Z + 1}Y + β^– + [v with bar above] + energy

The antineutrino is a very small uncharged particle that goes undetected by clinical nuclear imaging apparatus and has no significant effect on the patient. The effect of β^– decay is the conversion of a neutron to a proton, producing an element with increased atomic number Z and with no change in atomic mass number A (an isobaric transition). The emitted beta particle has a spectrum of energies up to a maximum energy. Many nuclear fission products are proton deficient and undergo β^– decay (Figure 8.4).

Beta particles demonstrate limited penetration of soft tissues and detector materials compared with gamma rays, and are not effectively detected by clinical nuclear medicine camera systems. Pure beta emitters are therefore not used for diagnostic imaging. However, some isotopes, including phosphorus-32 and yttrium-90 are employed as therapeutic agents in clinical nuclear medicine. Their in vivo distribution following radioisotope therapy can be demonstrated by imaging the bremsstrahlung radiation they generate (Figure 8.5).

Decay schemes illustrate radioactive decay graphically. The horizontal axis represents atomic number, and the vertical axis represents energy. The higher energy parent appears at the top of the diagram, and the lower energy daughter(s) appear to the left or right. For beta emitters such as P-32, the daughter has Z + 1 compared with the parent, and thus lies to the right (Figure 8.6).

FIG. 8.4 • Beta decay. A proton-deficient radionuclide emits a beta particle (−) and an antineutrino ([v with bar above]). The result is a daughter nuclide with an increase in atomic number and no change in atomic mass number.

FIG. 8.5 • Bremsstrahlung single-photon emission computed tomography/computed tomography following selective internal radiation therapy with Y-90 microspheres demonstrates the expected distribution of the microspheres within the liver, and no significant extrahepatic activity.

FIG. 8.6 • Principal decay scheme of phosphorus-32. Reprinted with permission from Bushberg JT, Seibert JA, Leidholdt EM, Boone JM. Essential Physics of Medical Imaging. 3rd ed. Philadelphia, PA: Wolters Kluwer Health/Lippincott Williams & Wilkins; 2012.

(β⁻, γ) emission

Following beta emission, the daughter nuclide may temporarily exist in one or more excited states, subsequently giving one or more gamma rays to reach the stable state.

^A_ZX → ^A_{Z + 1}Y^* + β^– + [v with bar above] + energy

^A_{Z + 1}Y^* → ^A_{Z + 1}Y + γ

The total energy of the beta particle, neutrino, and gamma ray is equal to the transition energy for the reaction. There may be many different possible combinations of energies given off during beta decay of a radioisotope (Figure 8.7).

The gamma ray from (β^–, γ) emission may be imaged by nuclear medicine gamma cameras. For example, this may be useful to demonstrate treated lesions following therapy with (β^–, γ) emitter I-131 for thyroid cancer (Figure 8.8). However, owing to the radiation dose imparted by the beta particle, (β^–, γ) emitters are not routinely used for clinical nuclear imaging.

β^– decay (positron emission)

Neutron-deficient isotopes may undergo positron emission (beta-plus decay). For example, positron emitter carbon-11 (¹¹C) has a lower atomic mass than does the common, stable isotope, carbon-12 (¹²C). This difference is due to the presence of six neutrons on the ¹²C nucleus, but only five neutrons in the ¹¹C nucleus. This neutron deficiency is responsible for the instability of ¹¹C.

In positron emission, a proton is effectively converted to a neutron, positron β⁺, and neutrino ν, with concomitant decrease in atomic number Z and no change in atomic mass number A (an isobaric transition).

^A_ZX → ^A_{Z − 1}Y + β⁺ + ν + energy

The positron is the antiparticle of the electron. It has unit positive charge, a mass identical to that of the electron, and a variable amount of kinetic energy. The positron travels some distance from the site of its generation as it loses kinetic energy, and the distance is generally greater for more energetic positrons. The emitted positron eventually loses sufficient kinetic energy that it is able to interact with an electron, with which it is mutually attracted. Both particles convert all of their rest mass to energy, which is released in the form of two 511 keV photons emitted approximately 180° apart. (By the law of conservation of momentum, the photon pair will conserve the momentum of the positron-electron pair, and therefore the two photons’ paths will be slightly <180° apart if the positron is not completely at rest at the beginning of the interaction.) This event is known as annihilation (see Figure 8.9).

The 1.022 MeV energy released in annihilation is the minimum transition energy necessary for positron emission to occur.

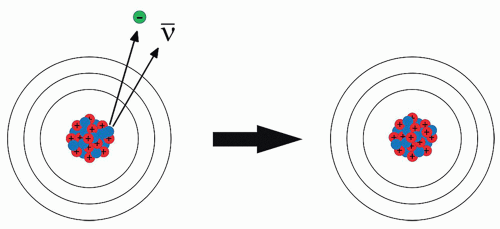
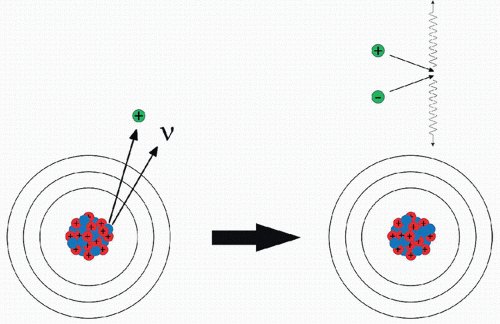
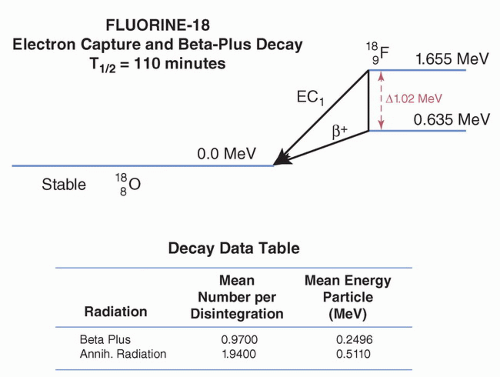
Below this threshold, positron emission does not take place, but the neutron-deficient isotope may undergo electron capture, discussed later. Above the threshold, electron capture may compete with positron emission. This threshold is also reflected in the minimum mass difference between the parent and daughter atoms required for positron emission. Like the antineutrino seen in β^– decay, the neutrino does not significantly interact with the patient or the clinical nuclear imaging system (Figure 8.10).

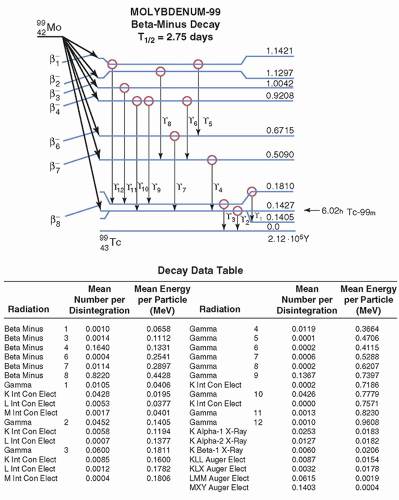FIG. 8.7 • Principal decay scheme of Mo-99. The many possible radiation decay products are listed on the accompanying decay data table.

FIG. 8.8 • I-131 posttherapy images. Anterior and posterior whole-body images obtained 5 days following therapy for thyroid cancer with I-131 demonstrate uptake within cervical, mediastinal, and upper abdominal lymph nodes, pelvic bones, and a left-sided rib, consistent with metastatic disease. Activity within the liver, bowel, nose, and mouth is physiologic. Diffuse activity on the skin of the feet is due to perspiration.

FIG. 8.9 • Positron emission. A neutron-deficient radionuclide emits a positron (+) and a neutrino (ν), resulting in a daughter nuclide with a decrease in atomic number and no change in atomic mass number. When the positron loses energy, it interacts with an electron to form two 511 MeV photons directed approximately 180° apart.

Positron emitters used in clinical applications are usually cyclotron produced or generator produced. These radioisotopes, such as fluorine-18, nitrogen-13, rubidium-82, carbon-11, and gallium-68, are widely employed in PET (Table 8.3).

Electron Capture

Electron capture provides a second mechanism for the neutron-deficient radioisotope to increase stability (Figure 8.11). An orbital electron, usually from the K or L shell, combines with a proton in the nucleus. This results in conversion of a proton to a neutron and liberation of a neutrino ν, producing a daughter with decreased atomic number Z and unchanged atomic mass number A (an isobaric transition).

^A_ZX + e− → ^A_{Z − 1}Y + v + energy

FIG. 8.10 • Principal decay scheme of fluorine-18. Reprinted with permission from Bushberg JT, Seibert JA, Leidholdt EM, Boone JM. Essential Physics of Medical Imaging. 3rd ed. Philadelphia, PA: Wolters Kluwer Health/Lippincott Williams & Wilkins; 2012.

Energy may be released as gamma rays from the nucleus, or as characteristic X-rays and Auger electrons from filling the vacancy left by the captured orbital electron.

Electron capture is the decay mode for neutron-deficient radioisotopes below the 1.022 MeV threshold. Isotopes with transition energies above this threshold may undergo electron capture, positron emission, or both (see Figure 8.10). Heavier elements, which have orbital electrons closer to the nucleus, tend to favor electron capture, and lighter elements favor positron emission. As with positron emitters, neutron-deficient radioisotopes undergoing electron capture are frequently cyclotron produced. Example isotopes used in clinical practice include gallium-67, indium-111, iodine-123, thallium-201, and cobalt-57.

Isomeric Transition

Isomeric transition occurs in nuclides undergoing transition from a metastable state to a stable state. Following nuclear transformations, nuclei may temporarily exist in excited states, releasing gamma rays as they decay to their stable form. This phenomenon has been demonstrated in the case of (β^–, γ) emission mentioned earlier (see Figure 8.7). When this initial excited state decays with a relatively long half-life, it is termed a metastable state, denoted by “m.” The decay involves liberation of energy from the nucleus,
and does not involve the gain or loss of particles as in other decay modes discussed (Figure 8.12).

Table 8.3 FDA-APPROVED PET RADIOPHARMACEUTICALS

Carbon-11 choline

Fluorine-18 florbetaben (Neuraceq)

Fluorine-18 florbetapir (Amyvid)

Fluorine-18 fludeoxyglucose (FDG)

Fluorine-18 fluciclovine (Axumin)

Fluorine-18 flutemetamol (Vizamyl)

Fluorine-18 sodium fluoride

Gallium-68 dotatate (Netspot)

Nitrogen-13 ammonia

Rubidium-82 chloride (Cardiogen-82)

Abbreviations: FDA, U.S. Food and Drug Administration; FDG, fluorodeoxyglucose; PET, positron emission tomography.

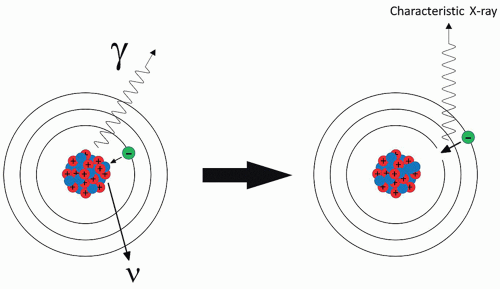FIG. 8.11 • Electron capture. A neutron-deficient radionuclide incorporates an inner shell electron into the nucleus with emission of a neutrino (ν) and a gamma ray. The vacancy may be filled by an outer shell electron and will result in characteristic X-rays or Auger electrons. The daughter nuclide has a decreased atomic number and an unchanged atomic mass number.

Only gold members can continue reading. Log In or Register to continue