Fig. 1
Top row: Yeast cells in different concentrations recorded by transmission microscopy. Bottom row: Yeast cells in different concentrations recorded by DIC microscopy and the reconstructed OPL map. Note the wide variations in image quality
In DIC microscopy the phase gradient is measured. For image processing this scan type is difficult to analyse directly. By a deconvolution method adapted to the DIC microscope [5] we can transform the DIC image into an intermediate image (bottom row right of Fig. 1) with an appearance similar to a fluorescence image. The deconvolution replaces the measured phase gradient by an optical path length (OPL) map. We will further use the OPL image for segmentation.
1.1 PDE methods
The task of automatic segmentation is to find coherent regions that relate to objects the observer is interested in. Typically, these regions are bounded and the boundary of objects are often found as the location where the intensity changes significantly. However, methods that use such edge information only, perform unsatisfactory as locally this edge information may be missing. In order to find edges at these locations, iterative schemes can be used that are based on Partial Differential Equations (PDEs). Roughly speaking, these PDEs are designed using driving forces that evolve curves towards edges. Usually, the PDE contains an edge detector which depends on the gradient of the image. Alternatively, a homogeneous area detector can be used which favours areas without much intensity changes. To minimise the influence of noise and missing information, constraints that penalise (for instance) the length of edges are added.
Examples of such approaches relate for instance to the active contour model [6], and modifications of it. The initial curve is to be placed around the object to be detected. The curve moves in the normal dimension to itself and ideally stops at the boundary of the object. The main drawbacks of the original snakes are their sensitivity to initial conditions and the difficulties associated with topological transformations.
Other approaches arise from the Mumford-Shah model [11]. It minimises a proposed energy of an image. This energy depends on piecewise smooth approximations for the given image. Although the model has its mathematical peculiarities, it formed the basis of many segmentation algorithms. For an overview of the ample literature on geometric pde models in image analysis, one can consult the collections of papers in e.g. [9, 13, 15].
1.2 Level set methods
A drawback of many PDEs approaches is the computation time. Often, the discretisation scheme requires small time steps in order to maintain a stable evolution. Secondly, PDE methods require an initial guess, which may heavily influence the final result. Thirdly, as one doesn’t know the number of objects at forehand, the number of available edge contours has to be flexible.
A framework that overcomes these problems to a large extent use level sets, initiated by Osher and Sethian [14, 18]. It exploits mathematical properties of equations of the form
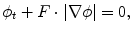
where F is a function that is user-defined. It can, for example, contain edge information. This model is applied in a wide variety of applications, see e.g. [9, 12, 13, 19].
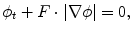
(1)
In image segmentation, one can think of ϕ being (a level line of) the image that evolves as a function of its gradient, or, more explicitly: as the evolution of edges towards their mathematically optimal position. The level set framework allows for a flexible setup, as it is able to split and merge curves during the process. To some extent, this also overcomes the initialisation problem. Finally, fast methods are available for implementation [8, 10].
1.3 Cell segmentation
In cell segmentation, impressive results using this methodology can be reached [3, 20, 21] when the cells are no too clustered and when they do not contain too much sub-structure. However, when they do, even these methods fail. An example is given in Fig. 2, where the implementation by Li et al. is used [8]. The optimal solution finds a set of clustered cells, since in this case the length of the edge curve is smallest. Relaxing the edge-length constraint results in segmenting dark sub-structures. An example of this can be seen in Fig. 3.



Fig. 2
Level Set implementations may fail. From left to right: The initial contour; results after 100, 1000, and 2000 iterations

Fig. 3
Segmentation result of the Multiphase Chan-Vese model. From left to right: original image; initial condition; final contour after 2000 iterations, μ = 0. 0015 ⋅ 2552; final phase
In the next two sections we present extensions of two general methodologies that use PDEs in a level-set framework. Firstly, we use a pre-processing step in Sect. 2 to get useful results for the Chan-Vese model [27]. Secondly, in Sect. 3 we combine a voting method for the cell centre with geometric PDEs [7]. Full details on the methodology and comparison with related methods can be found in [28].
2 The Chan-Vese Level Set Method
Chan and Vese [1] proposed a model for image segmentation based on the Mumford-Shah functional and level sets. This model does not explicitly depend on the gradient of the image. It therefore performs well in images with ambiguous boundaries. The model is defined as the following minimisation problem [1, 2]: Given the original image u 0 in Ω and two unknown constants c 1 and c 2 in the inside and outside region, respectively, which are separated by the curve δ(ϕ) | ∇ϕ | , minimise the following energy with respect to c 1, c 2 and ϕ:
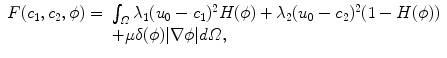
where H denotes the Heaviside function and δ the Dirac measure. The first and second term penalise the L 2 distance in the inside and outside regions, and the third term measures the length of the curve.
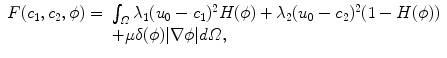
(2)
2.1 The multiphase level set method
The traditional Chan-Vese model can segment the image into two regions – background and foreground. In order to segment images into more regions, a Multiphase Level Set Method has been developed [4, 23]. It is motivated by the Four Colour Theorem which states that only four colours are enough to dye all the regions in a partition. Therefore, only two level set functions will suffice to represent any partition. The multiphase level set method is the direct extension of Eq. (2) and is defined as follows:
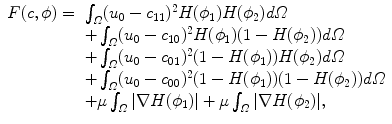
where the first four integrals compute the L 2 distance of a constant c ij to u 0 in each of the four difference regions (![$$c_{11} \in \{ (x,y):\phi _{1} > 0,\phi _{2} > 0\}$$
” src=”/wp-content/uploads/2016/09/A151032_1_En_26_Chapter_IEq1.gif”></SPAN>, etc.). The Euler-Lagrange equations obtained by minimising Eq. (<SPAN class=InternalRef><A href=]() 3) with respect to c and ϕ are:
3) with respect to c and ϕ are:
![$$\displaystyle{ \begin{array}{cl} \frac{\partial \phi _{1}} {\partial t} =&\delta _{\epsilon }(\phi _{1})\{\mu \cdot \mbox{ div}( \frac{\nabla \phi _{1}} {\vert \nabla \phi _{1}\vert }) \\ & - [((u_{0} - c_{11})^{2} - (u_{0} - c_{01})^{2})H(\phi _{2}) \\ & + ((u_{0} - c_{10})^{2} - (u_{0} - c_{00})^{2})(1 - H(\phi _{2}))]\}, \end{array} }$$](/wp-content/uploads/2016/09/A151032_1_En_26_Chapter_Equ4.gif)
![$$\displaystyle{ \begin{array}{cl} \frac{\partial \phi _{2}} {\partial t} =&\delta _{\epsilon }(\phi _{2})\{\mu \cdot \mbox{ div}( \frac{\nabla \phi _{2}} {\vert \nabla \phi _{2}\vert }) \\ & - [((u_{0} - c_{11})^{2} - (u_{0} - c_{10})^{2})H(\phi _{1}) \\ & + ((u_{0} - c_{01})^{2} - (u_{0} - c_{00})^{2})(1 - H(\phi _{1}))]\}.\end{array} }$$](/wp-content/uploads/2016/09/A151032_1_En_26_Chapter_Equ5.gif)
Furthermore, c ij = | u 0 | in the regions where they are defined.
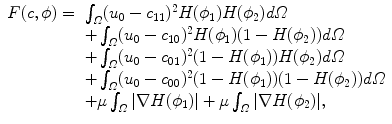
(3)
![$$\displaystyle{ \begin{array}{cl} \frac{\partial \phi _{1}} {\partial t} =&\delta _{\epsilon }(\phi _{1})\{\mu \cdot \mbox{ div}( \frac{\nabla \phi _{1}} {\vert \nabla \phi _{1}\vert }) \\ & - [((u_{0} - c_{11})^{2} - (u_{0} - c_{01})^{2})H(\phi _{2}) \\ & + ((u_{0} - c_{10})^{2} - (u_{0} - c_{00})^{2})(1 - H(\phi _{2}))]\}, \end{array} }$$](/wp-content/uploads/2016/09/A151032_1_En_26_Chapter_Equ4.gif)
(4)
![$$\displaystyle{ \begin{array}{cl} \frac{\partial \phi _{2}} {\partial t} =&\delta _{\epsilon }(\phi _{2})\{\mu \cdot \mbox{ div}( \frac{\nabla \phi _{2}} {\vert \nabla \phi _{2}\vert }) \\ & - [((u_{0} - c_{11})^{2} - (u_{0} - c_{10})^{2})H(\phi _{1}) \\ & + ((u_{0} - c_{01})^{2} - (u_{0} - c_{00})^{2})(1 - H(\phi _{1}))]\}.\end{array} }$$](/wp-content/uploads/2016/09/A151032_1_En_26_Chapter_Equ5.gif)
(5)
The only varying parameter in the model is the coefficient of the length term μ. This term affects the length of the final contour. The smaller μ is, the longer the final contour is. So if we want to detect as many objects as possible (for example, segment all cells), the μ should be small. If we are only interested in large objects and do not want to detect small objects (for example, the sub-structure inside the cell, cf. Fig. 2), μ should be large. However, these two requirements contradict each other as we want both.
Figure 3 shows the result applying the Multiphase Chan-Vese model with a small value of μ. It manages to find the individual cells, but only at the cost of sub-segmenting the cells. The segmentation criterion for Chan-Vese based models is the average grey level of an object, cf. Eq. (3). For piecewise constant objects, the performance of this model is therefore excellent. However, real cells always contain sub-structures inside them, which will cause a false segmentation. Furthermore, in some cell images, the grey level difference between the cells and background is not distinct. Therefore, a pre-processing method is needed to solve these problems.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree