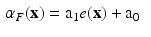and capture the whole volume of the isolated heart (approx. 1 1
1 2 cm
2 cm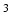 ).
).
2.2 Data Preprocessing
Slicewise segmentation and labeling was performed by visual inspection, discriminating the left and right ventricle and excluding the surrounding container volume, non-tissue artifacts and cavities from the analysis.
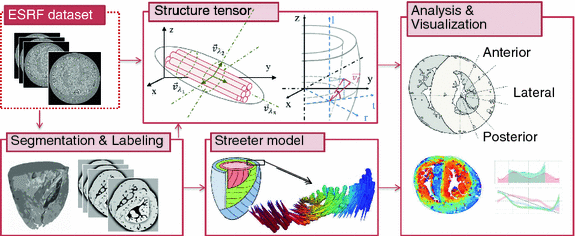

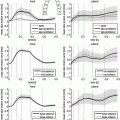
Fig. 1.
Schematic display of the analysis performed on the phase-contrast dataset. The structure tensor box includes a scheme of a fiber system defined with eigenvectors 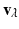 obtained by tensor eigenanalysis, and the assumed cardiac cylindrical coordinate system defined with r-radial, t-tangential and l-longitudinal component. The Streeter model box displays the expected fiber orientation in a whole heart and a transmural patch. The evaluation box shows the sectors selected for quantification of results.
obtained by tensor eigenanalysis, and the assumed cardiac cylindrical coordinate system defined with r-radial, t-tangential and l-longitudinal component. The Streeter model box displays the expected fiber orientation in a whole heart and a transmural patch. The evaluation box shows the sectors selected for quantification of results.
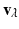 obtained by tensor eigenanalysis, and the assumed cardiac cylindrical coordinate system defined with r-radial, t-tangential and l-longitudinal component. The Streeter model box displays the expected fiber orientation in a whole heart and a transmural patch. The evaluation box shows the sectors selected for quantification of results.
obtained by tensor eigenanalysis, and the assumed cardiac cylindrical coordinate system defined with r-radial, t-tangential and l-longitudinal component. The Streeter model box displays the expected fiber orientation in a whole heart and a transmural patch. The evaluation box shows the sectors selected for quantification of results.2.3 Gradient Structure Tensor
For calculating the myofiber orientation, a gradient structure tensor method was applied. For each voxel ![$$\mathbf {x}=[x,y,z]$$](/wp-content/uploads/2016/09/A339585_1_En_13_Chapter_IEq6.gif) in the image
in the image 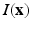 , the oriented gradient magnitudes in x, y and z-directions were obtained using a central difference algorithm, resulting in a gradient vector
, the oriented gradient magnitudes in x, y and z-directions were obtained using a central difference algorithm, resulting in a gradient vector ![$$\mathbf {g}(\mathbf {x}):=\nabla I(\mathbf {x})= [g_x\mathbf {(x)}, g_y\mathbf {(x)},g_z\mathbf {(x)}]$$](/wp-content/uploads/2016/09/A339585_1_En_13_Chapter_IEq8.gif) . The structure tensor in a voxel is defined as
. The structure tensor in a voxel is defined as 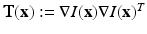 , however, here information is gathered over a voxel’s cubical neighborhood
, however, here information is gathered over a voxel’s cubical neighborhood 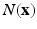 as a linear combination of the belonging structure tensors, resulting in an local structure tensor estimation
as a linear combination of the belonging structure tensors, resulting in an local structure tensor estimation 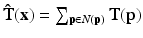 , which is in a matrix notation:
, which is in a matrix notation:
![$$\begin{aligned} \mathbf {\hat{T}} = \left[ \begin{matrix} \sum {{g_x}^2} &{} \sum {g_x g_y} &{} \sum {g_x g_z} \\ \sum {g_y g_x} &{} \sum {{g_y}^2} &{} \sum {g_y g_z} \\ \sum {g_z g_x} &{} \sum {g_z g_y} &{} \sum {{g_z}^2} \end{matrix} \right] \end{aligned}$$](/wp-content/uploads/2016/09/A339585_1_En_13_Chapter_Equ1.gif)
Eigen-decomposition of the structure tensor (Eq. 2) transforms the given gradient space into a space defined with orthogonal vectors 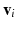
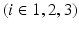 , encoding the appearance of a tubular structure, i.e. fiber (Fig. 1):
, encoding the appearance of a tubular structure, i.e. fiber (Fig. 1):
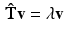
The smallest eigenvalue 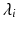 corresponds to the vector
corresponds to the vector 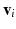 pointing in the fiber direction, while the largest eigenvalue, as opposed to MRI, is assumed to correspond to the vector pointing in the direction of the sheet normal [6]. For the smallest eigenvalue vector, the inclination angle
pointing in the fiber direction, while the largest eigenvalue, as opposed to MRI, is assumed to correspond to the vector pointing in the direction of the sheet normal [6]. For the smallest eigenvalue vector, the inclination angle 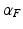 was calculated as an angle between the transverse plane and the vector projection to the local tangential plane of the cylindrical coordinate system of the heart, as illustrated in Fig. 1. In further text, we refer to this angle as fiber angle. Similarly, the transverse angle
was calculated as an angle between the transverse plane and the vector projection to the local tangential plane of the cylindrical coordinate system of the heart, as illustrated in Fig. 1. In further text, we refer to this angle as fiber angle. Similarly, the transverse angle 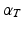 was calculated as the angle between the tangential plane and the vector projection to the transverse plane. These two angles for each voxel location
was calculated as the angle between the tangential plane and the vector projection to the transverse plane. These two angles for each voxel location 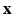 determine the local fiber vector orientation.
determine the local fiber vector orientation.
![$$\mathbf {x}=[x,y,z]$$](/wp-content/uploads/2016/09/A339585_1_En_13_Chapter_IEq6.gif) in the image
in the image 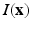 , the oriented gradient magnitudes in x, y and z-directions were obtained using a central difference algorithm, resulting in a gradient vector
, the oriented gradient magnitudes in x, y and z-directions were obtained using a central difference algorithm, resulting in a gradient vector ![$$\mathbf {g}(\mathbf {x}):=\nabla I(\mathbf {x})= [g_x\mathbf {(x)}, g_y\mathbf {(x)},g_z\mathbf {(x)}]$$](/wp-content/uploads/2016/09/A339585_1_En_13_Chapter_IEq8.gif) . The structure tensor in a voxel is defined as
. The structure tensor in a voxel is defined as 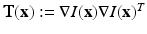 , however, here information is gathered over a voxel’s cubical neighborhood
, however, here information is gathered over a voxel’s cubical neighborhood 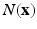 as a linear combination of the belonging structure tensors, resulting in an local structure tensor estimation
as a linear combination of the belonging structure tensors, resulting in an local structure tensor estimation 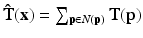 , which is in a matrix notation:
, which is in a matrix notation:![$$\begin{aligned} \mathbf {\hat{T}} = \left[ \begin{matrix} \sum {{g_x}^2} &{} \sum {g_x g_y} &{} \sum {g_x g_z} \\ \sum {g_y g_x} &{} \sum {{g_y}^2} &{} \sum {g_y g_z} \\ \sum {g_z g_x} &{} \sum {g_z g_y} &{} \sum {{g_z}^2} \end{matrix} \right] \end{aligned}$$](/wp-content/uploads/2016/09/A339585_1_En_13_Chapter_Equ1.gif)
(1)
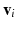
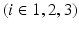 , encoding the appearance of a tubular structure, i.e. fiber (Fig. 1):
, encoding the appearance of a tubular structure, i.e. fiber (Fig. 1):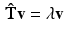
(2)
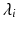 corresponds to the vector
corresponds to the vector 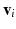 pointing in the fiber direction, while the largest eigenvalue, as opposed to MRI, is assumed to correspond to the vector pointing in the direction of the sheet normal [6]. For the smallest eigenvalue vector, the inclination angle
pointing in the fiber direction, while the largest eigenvalue, as opposed to MRI, is assumed to correspond to the vector pointing in the direction of the sheet normal [6]. For the smallest eigenvalue vector, the inclination angle 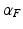 was calculated as an angle between the transverse plane and the vector projection to the local tangential plane of the cylindrical coordinate system of the heart, as illustrated in Fig. 1. In further text, we refer to this angle as fiber angle. Similarly, the transverse angle
was calculated as an angle between the transverse plane and the vector projection to the local tangential plane of the cylindrical coordinate system of the heart, as illustrated in Fig. 1. In further text, we refer to this angle as fiber angle. Similarly, the transverse angle 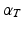 was calculated as the angle between the tangential plane and the vector projection to the transverse plane. These two angles for each voxel location
was calculated as the angle between the tangential plane and the vector projection to the transverse plane. These two angles for each voxel location 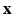 determine the local fiber vector orientation.
determine the local fiber vector orientation.The application of the structure tensor method to the fetal cardiac dataset resulted in a fiber vector field and corresponding angle maps.
2.4 Rule-Based Fiber Model
The histological studies [1] performed on cardiac fiber arrangement resulted in a translation of measurements into a mathematical formulation that can be applied to different cardiac geometries [17]. Thus, according to most detailed description for a whole heart available we generated the following Streeter model for the left ventricle (LV) extracted from our data for comparison with the structure tensor method. For each point 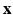 in the LV tissue, two distances are relevant: the smallest distance to the endocardium (
in the LV tissue, two distances are relevant: the smallest distance to the endocardium (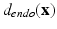 ) and to the epicardium (
) and to the epicardium (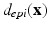 ). From these two, a normalized distance map is constructed as:
). From these two, a normalized distance map is constructed as:
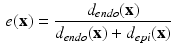
representing the normalized tissue thickness. The distance from the point to the base can be expressed with the polar angle 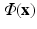 , with respect to the long axis, defined based on the mitral valve center
, with respect to the long axis, defined based on the mitral valve center 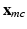 and apex
and apex 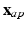 coordinates:
coordinates:
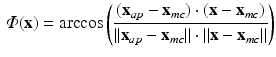
The relationship of the normalized distance and the base-distance with helix and transverse angle is now given with:
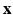 in the LV tissue, two distances are relevant: the smallest distance to the endocardium (
in the LV tissue, two distances are relevant: the smallest distance to the endocardium (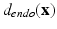 ) and to the epicardium (
) and to the epicardium (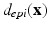 ). From these two, a normalized distance map is constructed as:
). From these two, a normalized distance map is constructed as: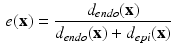
(3)
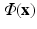 , with respect to the long axis, defined based on the mitral valve center
, with respect to the long axis, defined based on the mitral valve center 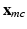 and apex
and apex 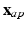 coordinates:
coordinates: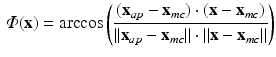
(4)