, Abas Sabouni2, Travis Desell3 and Ali Ashtari4
(1)
Department of Electrical Engineering, University of North Dakota, Grand Forks, ND, USA
(2)
Department of Electrical Engineering, Wilkes University, Wilkes-Barre, PA, USA
(3)
Department of Computer Science, University of North Dakota, Grand Forks, ND, USA
(4)
Invenia Technical Computing, Winnipeg, MB, Canada
Abstract
This chapter introduces common techniques used in developing evolutionary algorithms for distributed systems, providing a survey of different methods. Most of these methods are evaluated against a common suite of benchmark equations. Chapter 8 provides some common example equations, and we refer the reader to Tang et al. for a comprehensive overview (Tang et al., Benchmark functions for the cec2008 special session and competition on large scale global optimization, in Nature Inspired Computation and Applications Laboratory (USTC, China, 2007)). Strategies for single-population, multiple-population, and cellular algorithms are presented, and then particular emphasis is placed on the implementation used for optimizing FDTD, which uses asynchronous updates of the population to aid in scalability and improve performance. Results are presented for the performance of this implementation using CPU, GPUs, and hybrid CPU–GPU strategies for evaluation of the objective functions.
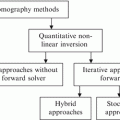
7.1 Survey of Parallel and Distributed Evolutionary Algorithms
A wide range of parallel and distributed evolutionary algorithms have been developed for use on different distributed computing environments, such as clusters, grids supercomputers, and even peer-to-peer networks. There are three general categories of parallel evolutionary algorithms: single population (panmictic, coarse-grained) [2–5]; multiple population (island, medium-grained) [6–10]; and cellular (fine-grained) [11–13], as classified by Cantu-Paz [14]. These various approaches have different effects on the explorative and exploitative properties of the evolutionary algorithms [15], with smaller subpopulations allowing faster exploitation of their areas of the search space.
Parallel and distributed EAs can also be synchronous, where entire populations are evaluated in parallel, and subsequent populations are generated when the fitness of the population is completely evaluated. These approaches are often simpler to program; however, processors can wait idle when the parallelization cannot be distributed evenly or when fitness evaluation is nondeterministic. Asynchronous approaches overcome this performance degradation by either allowing subpopulations or individuals to be updated independently without waiting for each other. In these approaches, populations evolve more gradually, as opposed to having fixed separate populations. Desell et al. have shown that performing evolutionary algorithms asynchronously can provide significant improvements to performance and scalability over iterative approaches [16–18].
It should be noted that while expanding an evolutionary algorithm to run in a distributed setting will change its general explorative and exploitative qualities, it is often possible to tweak the other parameters to the evolutionary algorithm in response to those changes, achieving similar performance.
7.1.1 Parallel Genetic Algorithms
Panmictic EAs create a population, evaluate it in parallel, and use the results to generate the next population. For this approach, there are three different approaches to parallelization. For a given population, each of the parameter sets in the generated population can be evaluated in parallel. This approach allows scalability up to population size used by the genetic search. Another approach is to parallelize the function evaluation and perform these iteratively for the whole population. For expensive and parallelized function evaluations, this allows as much scalability as the function evaluation can use. Lastly, a hybrid of the two approaches, parallel function evaluation done in parallel for each parameter set in the population can be done. This allows the greatest amount of scalability, but can be complicated to implement. Unfortunately, for nonparallel function evaluations or large-scale computing environments, none of these approaches may be able to use all the available resources.
Island approaches use multiple populations of parameter sets called islands. Typically, after a fixed number of iterations, the populations propagate their best parameter sets to the other populations. In these cases, each island can be parallelized in the same manner as a panmictic GA, which increases scalability. Additionally, it has been shown that super-linear speedup can be attained using this method, as smaller populations can converge to minima quicker than larger populations [7, 8]. However, having populations of different sizes and/or populations running on clusters of different speeds can have varying negative effects on the performance of the search.
Cellular algorithms [11, 12] evaluate individual parameter sets, then update these individual sets based on the fitness of their neighbors. Dorronsoro et al. have shown that asynchronous cellular GAs can perform competitively and discuss how the update rate and different population shapes affect the convergence rate [19].
P-CAGE [13] is a peer-to-peer (P2P) implementation of a hybrid multi-island genetic search built using the JXTA protocol [20] which is also designed for use over the Internet. Each individual processor (a member of the P2P network) acts as an island (a subpopulation of the whole) and evolves its subpopulation cellularly. Every few iterations, it will exchange exterior neighbors of its population with its neighbors.
There have also been different approaches taken in developing parallel GAs (PGAs) for computational grids. Imade et al. have studied synchronous island genetic algorithms on grid computing environments for bioinformatics [6], using the Globus Toolkit [21]. Lim et al. provide a framework for distributed calculation of genetic algorithms and an extended API and meta-scheduler for resource discovery [22]. Both approaches use synchronous island-style GAs. Nimrod/O [23] is a tool that provides different optimization algorithms for use with Nimrod/G [24].
7.1.2 Parallel Differential Evolution
Tasoulis et al. use parallel virtual machines (PVM) to implement a parallel differential evolution algorithm [9]. This algorithm generates a ring of subpopulations and, for each iteration, determines which individuals a subpopulation will migrate to the next in the ring. Individuals are probabilistically selected for migration via a user selected migration constant. They test this approach with a number of test equations: Sphere, Rosenbrock, Step, Quartic, Shekel’s Foxholes, Corona Parabola, and Griewank. In particular, they measure the effect on convergence as the migration constant changes. Intermediate values of the migration constant result in the best convergence rates, with values close to 0 or 1 resulting in significant increases in convergence time. As found in other research, the best/1/bin tended to be the most efficient on across the test functions; however, fine-tuning the migration constant resulted in comparable or better performance for other DE strategies. This work is further expanded upon by Parsopoulos et al. for multi-objective optimization [27].
7.1.3 Parallel Particle Swarm Optimization
Particle swarm optimization has also become popular for use in different parallel environments. Baskar et al. extend Fitness-Distance-Ratio PSO (FDR-PSO) for concurrent execution [28, 29]. FDR-PSO is introduced and analyzed by Peram et al. [30, 31] and is a modification of PSO that only selects a single other particle to modify a current particle’s direction. The particle chosen is the one with the highest FDR between a particle’s current value and another particle’s individual best:


(7.1)
Peram et al. show FDR-PSO to perform competitively with regular PSO without requiring social or cognitive terms. Baskar et al.’s approach makes this concurrent by utilizing two concurrent swarm populations: one using regular PSO and the other using FDR-PSO. At the end of each iteration, the global best particle of each population is shared between the two groups. Their results using optimizing reconfigurable phase-differentiated antenna arrays show that FDR-PSO and their concurrent PSO perform better than regular PSO and genetic search.
Schutte et al. examine parallel synchronous particle swarm for load-balanced analytical test problems and load-imbalanced biomedical system identification [2]. This method evaluates each particle in parallel for each iteration. Their results show that the parallel synchronous particle swarm performs well for the load-balanced test problems with near-linear improvement; however, for the load-imbalanced problems, performance degrades with the parallel version due to each iteration waiting for the slowest computation. From these results, they suggest that an asynchronous parallel PSO would be valuable.
Koh et al. implement a parallel asynchronous PSO for heterogeneous networks [4] using the MPI [32]. The algorithm uses an approach similar to CILK’s work stealing [33], where the master processor contains a queue of currently unevaluated particles and slave processors request particles to evaluate from the master. In this way the search proceeds similar to synchronous particle swarm, as when the result for a particle is reported to a master, the next position for that particle is generated and added to the queue of work. This approach ensures that each particle performs close to the same number of evaluations. The asynchronous method is shown to achieve nearly identical results to synchronous parallel PSO for homogeneous clusters; however, on their test heterogeneous cluster of 20 processors, the asynchronous version had a clear advantage in performance, reducing computation time by 3.5. Venter et al. use a similar asynchronous parallel PSO and analyze it for the design optimization of a typical transport aircraft wing with similar results [5].
Cui and Potok propose a distributed particle swarm optimizer that can find a solution which may be moving in a noisy search space [34]. Their approach works as a normal particle swarm, except that every time the new position of a particle is found to be worse than the local best, the fitness of the local best particle is degraded. In this way, if a particle continuously reaches bad new positions, there is a greater chance that the environment has changed and it will start performing a wider search. This is compared to other approaches which reset the particle swarm fitness every few iterations and those that use sentry particles to detect when to reset the swarm fitness. Their approach not only provides more accurate results as the environment changes, but is more suitable to distributed particle swarm because the only information it requires broadcasting is the global best particle.
Xu and Zhang use a master–slave model for parallel particle swarm for attribute reduction [3]. Their method is asynchronous, with each processor being assigned a particle and reporting information on new global best positions to the master. The master will broadcast new global best particles to all the slaves when they are found. As with other asynchronous approaches, their results show an improvement in convergence rates and effective convergence to global minima.
Prez and Basterrechea consider both global and local swarm topologies with asynchronous and synchronous update for parallel PSO [10]. The asynchronous PSO used performs as the method described by Koh and synchronous PSO as described by Schutte. For the global swarm topology, particles are drawn to the global best point, which is updated after every particle evaluation in the asynchronous version and between iterations for the synchronous version. The local swarm topology uses a local best (instead of a global best) which is the best of a set of N neighbors, typically 15 % of the swarm size. This work shows that for their example problems of array synthesis and planar near-field antenna measurements, asynchronous global PSO clearly outperforms the other versions in terms of time to convergence with an additional benefit of better utilization of heterogeneous resources; however, it should be noted that the local best approach has a wider search area and is more resistant to convergence to local minima.
7.2 Asynchronous Global Optimization

Fig. 7.1
A generic asynchronous search methodology for distributed computing systems. A population of the best known individuals and their fitness is stored and used to generate new individuals to evaluate. These unevaluated individuals are kept in a work queue which workers request work from. The work queue can request more work to be generated from the population (at any time) to ensure that work requests are answered as quickly as possible. Evaluated individuals are used to evolve the population when their results are reported by the workers
A generic strategy has been used to implement asynchronous versions of differential evolution, genetic search, and particle swarm optimization, as described in Sects. 3.2, 3.3, and 3.4, respectively. Figure 7.1 presents a generic asynchronous search methodology for distributed computing systems. A population of parameter sets is kept and used to generate new parameter sets which are placed in a work queue. Clients connect asynchronously and request parameter sets to evaluate from this work queue. New parameter sets are generated using different operations on the population when they are needed as the queue runs low. This can be used to reproduce any of the synchronous methods described in Chap. 3 so long as the results are processed synchronously—they are reported in the same order that they were generated.
This generic strategy for asynchronous search is extended through using different types of operators to generate new parameter sets filling up the work queue. For example, in genetic search or particle swarm optimization, the successive generation or particles would be placed on the work queue, and when these results were reported the population would be updated. The following sections describe modifications to differential evolution, genetic search, and particle swarm optimization that enable them to perform asynchronously using this asynchronous methodology.
7.2.1 Asynchronous Genetic Algorithms
Asynchronous algorithm search can most easily model traditional genetic algorithms and is extremely similar to steady-state genetic search. With the main difference being that instead of one parameter set being generated at a time in panmictic GAs, multiple are generated and evaluated asynchronously. Using this strategy, when new members need to be generated, different recombination operators are applied to randomly selected members of the population. When the fitness of a member is reported, it is then inserted in order into the population and the worst member of the population is then removed if the population size is greater than a fixed value. The member removed can be the member just reported. Example recombination operators include mutation, average, double shot, and probabilistic simplex. Children are generated using these recombination operators as follows:
Mutation works the same as in a traditional genetic algorithm: one parent is selected at random from the population, and one parameter is mutated. Each parameter typically has defined maximum and minimum values, and the mutation takes place anywhere within this range.
Average is also a standard operator in a traditional genetic algorithm. Two parents are selected at random from the population, and a child is generated where each parameter is the average of its parents’ parameters.
Double shot is an extension to the average operator that provides an improvement by converging faster to local minima and also adding an exploratory component. Two parents are selected at random, but instead of one child, three are generated. The first child is the average of the two parents, the second lower child is calculated as follows:

(7.2)
and the third child, higher, is calculated by
where the ith parameter of the lower and higher children are calculated using the ith parameter of the better parent and worse parent, respectively. In essence, the lower and higher children are generated outside of the parents, equally distant from the average and the distance between either parent and the child outside of it is the same as to the average.

(7.3)
Probabilistic simplex randomly generates a child along a line calculated using the simplex method. Different from other operators, this approach can use a variable number of parents. n parents are selected at random and a line is created through the worst parent and the centroid (or average) of the remaining parents. By selecting a random number, rand, between two limits, l 1 and l 2, the ith parameter of the child is calculated by
Using this equation, a random value of 1.0 would generate a child that is the centroid, 0 would be the worst, and 2.0 would be the reflection of the worst point through the centroid. For the astronomy application, the limits that have been tested are

(7.4) , l 2 = 1. 5, and
, l 2 = 1. 5, and  , l 2 = 2. 0, with the second set providing faster convergence.
, l 2 = 2. 0, with the second set providing faster convergence.
7.2.2 Asynchronous Particle Swarm Optimization
Particle swarm optimization is another population-based global optimization method, which makes it easily applicable to the asynchronous search framework presented in this chapter. However, as opposed to genetic algorithms, especially the steady-state variant, particle swarm is much more iterative in nature. Where in genetic algorithms, individuals are easily created and removed from the population, particle swarm takes a fixed number of particles and updates these iteratively by moving them in the same previous direction and pulling them toward the globally best position found and each particle’s locally best position found. Because of this, for the particle swarm method to be used by the asynchronous search framework, some modifications need to be made.
Asynchronous particle swarm works as follows. The search is initialized by having positions of particles generated at random with zero velocity until there has been a fitness reported for a possible position of each particle. The server keeps track of each particle’s current position and current velocity, generating new positions for particles in a round-robin fashion when work is requested. The newly generated particle is generated identically to the original particle swarm optimization algorithm described in Sect. 3.4, using the current locally best known position for that particle and the current globally best known position. As opposed to the approaches discussed in the related work (see Sect. 3.4) that only process one position per particle at a time, this approach continues to generate new future positions for particles and send them to workers, updating a particle’s current position without knowing the fitness of the previously generated points. Using this approach, multiple positions for a single particle can be calculated concurrently, and the search does not need to wait for unreported fitnesses. When a worker reports the fitness of a particle, it also reports the position and velocity of the particle reported. If the fitness of the reported particle is better than that particle’s locally best found position, that position is updated, and the velocity of the particle is reverted to the reported velocity. If the fitness is the globally best found fitness, the position of the global best particle is updated as well.
In this way, asynchronous particle swarm performs nearly identical to traditional particle swarm when the number of processors used is less than the number of particles and there are no faults; however, it can also scale to very large systems by letting workers evaluate possible future positions of a particle. For a large number of workers, the search is more exploratory, examining many possible future positions of a particle assuming the local and global best positions have not been updated. The approach is also resilient to unreported results (in case of hardware failures or nondeterminism), as more future positions of a particle are generated until one is found which improves that particle’s locally best found position. Additionally, as many generated positions for particles do not improve the global best fitness of the swarm, or a particle’s local best fitness, this strategy in a sense lets the search progress faster by generating multiple future positions of particles which can be evaluated concurrently.
7.2.3 Asynchronous Differential Evolution
Differential evolution has similarities between both genetic search and particle swarm optimization, utilizing multiple parents and recombination (reproduction in genetic search), as well as local and global population information (cognitive and social knowledge in particle swarm optimization). Similar to particle swarm optimization, the current value of an individual is used to generate that individual’s next value; however, differential evolution uses a monotonically improving strategy on an individual basis.
Differential evolution also has a large suite of different equations to generate the next iteration of an individual (see Sect. 3.2), which shows varying suitability for different test equations. The rand/1/bin and best/1/bin variants, for example, seem particularly robust with quick convergence for a wide range of test functions in both traditional single-population DE [35] and parallel DE with multiple populations [9].
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree