Before entering the issue of creating patient specific models, it is useful to structure those models into a hierarchy of three main levels [16], the knowledge of the lower level being required for the implementation of the upper level. The first level is mainly geometrical and addresses the construction of digital static descriptions of the anatomy, often based on medical imagery. The techniques for segmenting and reconstructing anatomical and pathological structures from medical images have been developed for the past 15 years and have brought many advances in several medical fields including computer-aided diagnosis, therapy planning, image-guided interventions, drug delivery, etc. An distinctive achievement of computational anatomy has been carried out by the “Visible Human Project” [1] which provided the first digital multimodal anatomical representation of the full human body.
A second level of modeling describes the physical properties of the human body, involving for instance the biomechanical behavior of various tissues, organs, vessels, muscles or bone structures [22].
A third level of modeling describes the functions of the major biological systems [24, 38] (e.g. cardiovascular [5, 44], respiratory [25], digestive, hormonal, muscular, central or peripheral nervous system, etc.) or some pathological metabolism (e.g. evolution of inflammatory or cancerous lesions [48], formation of vessel stenoses [7, 42], etc.). Such physiological models often include reactive mechanisms while physical models only provide a passive description of tissues and structures.
There is an additional dimension associated with each level: the scale at which the anatomical, physical or physiological structure is described. With the development of new imaging modalities, it is now possible to observe the shape or function of most structures at the macroscopic (tissue), microscopic (cellular) levels and even in such cases to reveal the metabolic activity at the nanoscopic (molecular) scale. Coupled with those multiscale observations are new generations of multiscale computational models [24, 38]
Furthermore, each model is specified by a number of parameters (e.g. material stiffness or electrical conductivity for a physical model) and a related task consists in finding a set of those parameters that produces the best agreement between the simulated processes (deformation, activation,…) and the observed ones. The techniques consisting in finding the patient-specific parameters of a dynamic model typically require to solve an inverse problem and are sometimes called “data assimilation” techniques in the field of oceanography or climatology. As illustrated in Fig. 2, the personalization of a model from medical images or signals is often a requirement for using its predictive power in clinical applications such as therapy planning or simulation. The personalized models may also be used as advanced image processing tools that can provide a decision support system with additional physical or physical parameters relevant for establishing a diagnosis.
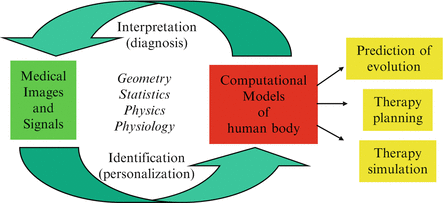

Fig. 2
This diagram shows how computational models can be coupled with medical images and signals to build personalized models and use them in clinical applications [4]
Finally, the ability to recover patient-specific parameters leads to the variability study of those parameters across a given population. Thus, statistical modeling of those computational models can be seen as an orthogonal modeling activity that aims for instance at finding the local or global similarities and dissimilarities of a structure or a function between two populations [18, 34, 49]. Statistical findings may also be used to calibrate, refine or constrain [11] a given model. At the basis of this activity is the growing availability of large databases of subjects and patients including biomedical signals and images as well as genetic information.
In the next sections, following the proposed hierarchy, we describe a number of practical cases involving the personalization of computational models before proposing some perspectives and challenges for future research.
2 Patient Specific Biomechanical/Physical modeling
Anatomical models only provide a static geometrical representation of the patient anatomy and do not take into account the deformation of soft tissue that may occur before or during therapy. To address this issue, it is necessary to add a biomechanical model that can estimate soft tissue deformations under the application of known forces or displacements. The additional complexity of modeling may be used to improve the pre-operative planning of a therapy [23, 43] or to provide advanced surgical gesture training.
Personalization of biomechanical models mainly involves the estimation of material parameters and boundary conditions from a time series of images, before and after deformation. One should stress the importance of specifying the proper boundary conditions (constraining the displacement of some nodes at the boundary of the structure) when modeling soft tissue deformation since it has a key effect of the displacement of neighboring nodes.
We briefly discuss below two limit cases for the personalization of biomechanical models: small deformations involved in brain-shift during neurosurgery and large deformations involved in liver surgery simulation.
2.1 Brain-Shift modeling in neurosurgery
The brain shift that occurs during a neuro-surgical intervention is the main source of intra-operative localization inaccuracies of pathologies (cerebral tumors, ). Indeed, a neurosurgeon establishes the surgical plan based on a pre-operative MR image: any non-rigid motion of the brain between the pre-operative and the intra-operative configuration may lead to an error in the localization of the target. To model the brain motion after opening the dura, a number of authors [17, 32] have made the hypothesis that the loss of cerebro-spinal fluid causes a pressure field along the gravity direction (Archimedes principle). Furthermore, anatomical constraints (falx cerebri, skull) of the deformation field can be enforced with a biomechanical model of the brain discretized as a tetrahedral mesh since the relevant anatomical information can be extracted from MR images and enforced on the mesh.
). Indeed, a neurosurgeon establishes the surgical plan based on a pre-operative MR image: any non-rigid motion of the brain between the pre-operative and the intra-operative configuration may lead to an error in the localization of the target. To model the brain motion after opening the dura, a number of authors [17, 32] have made the hypothesis that the loss of cerebro-spinal fluid causes a pressure field along the gravity direction (Archimedes principle). Furthermore, anatomical constraints (falx cerebri, skull) of the deformation field can be enforced with a biomechanical model of the brain discretized as a tetrahedral mesh since the relevant anatomical information can be extracted from MR images and enforced on the mesh.
 ). Indeed, a neurosurgeon establishes the surgical plan based on a pre-operative MR image: any non-rigid motion of the brain between the pre-operative and the intra-operative configuration may lead to an error in the localization of the target. To model the brain motion after opening the dura, a number of authors [17, 32] have made the hypothesis that the loss of cerebro-spinal fluid causes a pressure field along the gravity direction (Archimedes principle). Furthermore, anatomical constraints (falx cerebri, skull) of the deformation field can be enforced with a biomechanical model of the brain discretized as a tetrahedral mesh since the relevant anatomical information can be extracted from MR images and enforced on the mesh.
). Indeed, a neurosurgeon establishes the surgical plan based on a pre-operative MR image: any non-rigid motion of the brain between the pre-operative and the intra-operative configuration may lead to an error in the localization of the target. To model the brain motion after opening the dura, a number of authors [17, 32] have made the hypothesis that the loss of cerebro-spinal fluid causes a pressure field along the gravity direction (Archimedes principle). Furthermore, anatomical constraints (falx cerebri, skull) of the deformation field can be enforced with a biomechanical model of the brain discretized as a tetrahedral mesh since the relevant anatomical information can be extracted from MR images and enforced on the mesh.This clinical problem has motivated the study of the biomechanical behavior of the brain. For instance, Miller [33] has proposed a rheological model for swine brains valid for large displacements. However, in most cases, authors have relied on linear elastic models to extrapolate displacement fields [17, 47] from the cortex surface. Similarly, partial validation of brain shift models has been carried out [10] with a linear elastic model by comparing computed displacements with those observed from intra-operative MR images.
The fairly good predictive power of those simplified models show that a quasi-incompressible (Poisson ratio close to 0. 5) linear elastic model is a good choice for simulating the small displacements induced by the brain shift. This is a sensible result since any non-linear material can be approximated as a linear elastic material for sufficiently small displacements. Another important point that makes the personalization of those biomechanical models less difficult is the fact they are often used to predict displacements from given imposed displacements. In such cases, the knowledge of the Young Modulus is irrelevant and only the Poisson ratio and the boundary conditions must be chosen properly.
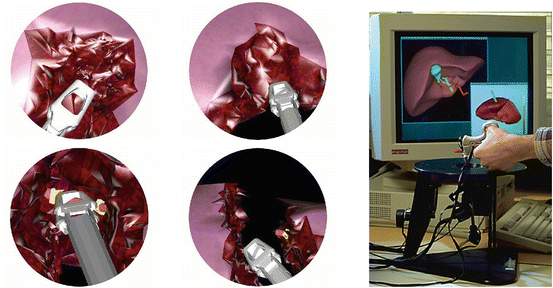
2.2 Hepatic Surgery Simulation
Surgery simulation aims at reproducing the visual and haptic senses experienced by a surgeon during a surgical procedure, through the use of computer and robotics systems. The medical scope of this technology is linked with the development of minimally invasive techniques especially videoscopic surgery (endoscopy, laparoscopy,…) and possibly telesurgery.
By creating patient-specific models, surgery simulation allows surgeons to verify, optimize and rehearse the surgical strategy of a procedure on a given patient.
However, an important issue for patient-specific soft-tissue models is the estimation of their material properties. Such parameters may be the Young Modulus and Poisson ratios for linear elastic materials or other stiffness parameters for general hyperelastic materials. There are three different sources of rheological data to estimate those parameters: ex-vivo testing where a sample of a tissue is positioned inside a testing rig [39]; in-vivo testing where a specific force and position sensing device is introduced inside the abdomen to perform indentation [8, 37]; Image-based elastometry from ultrasound, Magnetic Resonance Elastometry [26, 31] or CT-scan imaging.
There is no consensus on which method is best suited to recover meaningful material parameters, each one having its limitation. For instance ex-vivo testing may not be relevant because of the swelling or drying of the tissue. In-vivo experiments should also be considered with caution because the response may be location-dependent (linked to specific boundary conditions or non-homogeneity of the material) and the influence of the loading tool caliper on the deformation may not be well understood. Finally elastometry commonly assumes that the tissue undergoes small displacements and need to be thoroughly calibrated.
Thus, when assessing the mechanical parameters of the liver, several authors have reported widely varying parameters [15]. It is especially difficult in the case of the liver because it undergoes large displacements and its perfusion affects deeply its rheology (the liver receives one fifth of the total blood flow at any time). In fact, trying to estimate the liver Young Modulus is prone to large errors because the liver response largely depends on the speed at which the pressure was applied. One can expect to obtain meaningful material parameters only if this material is highly viscoelastic such as the one proposed by Kerdork et al. [27].
Furthermore, in a surgical simulator there are strict real-time constraints for simulating soft tissue deformations. For instance, the required refresh rate for user interaction is 30 Hz for visual feedback and more than 500 Hz for force-feedback, although the latter constraint can be alleviated with the addition of a local haptic model [20]. This implies that specific optimisations of soft tissue deformation must be devised either in the form of precomputations [15], or dedicated data structures [40] or multigrid [14] algorithms.
Thus, providing patient-specific soft tissue deformation suitable for surgery simulation remains largely an open problem that encompasses two separate issues. The former one corresponds to the proposition of a physically realistic constitutive material (with viscoelastic and non-linear behaviours) that is suitable for real-time computation. The latter one consists in finding reliable and non-invasive ways to estimate those material parameters from in-vivo data.
3 Patient Specific Physiological Modeling
To model the active properties of living tissues and the dynamic nature of normal or pathological evolving processes, it is necessary to introduce physiological models of the human body. We illustrate the personalization of those models with two examples related to the modeling of the electro-mechanical activity of the heart and the growth of brain tumors.
3.1 Cardiac modeling
During the past 15 years, a scientific INRIA consortium1 has developed an electro-mechanical model of the cardiac ventricles for medical purposes. The model reproduces the electrical depolarization and repolarization of the cardiac tissues through a set of macroscopic reaction-diffusion equations initially proposed by Fitzugh and Nagumo [19] and further refined by Aliev and Panvilov [2].
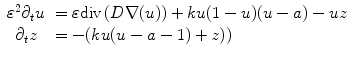
where u is the action potential averaged within a volume element of the cardiac tissue, z is the repolarization variable, D is the electrical conductivity tensor, 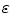 is a numerical constant, k controls the electrical reaction and a controls the action potential duration.
is a numerical constant, k controls the electrical reaction and a controls the action potential duration.
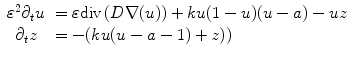
(1)
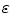 is a numerical constant, k controls the electrical reaction and a controls the action potential duration.
is a numerical constant, k controls the electrical reaction and a controls the action potential duration.The electrical activity can be synchronized with the actual ECG (electro-cardiogram) of the patient and creates a mechanical contraction followed by an active relaxation which are modeled by a set of partial differential equations initially proposed by Bestel, Clément and Sorine [6]. The average direction of the myocardium fibers is also integrated into this model (for instance through the conductivity tensor D), since it plays an important role in the anisotropic propagation of both the electrical and mechanical excitations.
This electromechanical model of the heart includes several parameters related to the heart anatomy (fiber orientation), electrophysiology (electrical conductivity), blood flow (preload and afterload) or cardiac mechanics (passive stiffness, contractility). It was shown in [44] that this model could be interactively adjusted to the actual geometrical, mechanical or electrical properties of patient’s heart through the use of conventional or tagged MR images and some in vivo electrophysiological measurements.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree