Perfusion Magnetic Resonance Imaging
David C. Alsop
Introduction
Perfusion is a fundamental physiologic quantity that can offer important diagnostic information about the condition of abnormal tissue. Perfusion can characterize the condition of the vasculature because blood flow in large vessels supplies the perfusion of tissue. It can also be an indicator of ischemic risk for tissue because ischemic injury is a direct result of hypoperfusion. Finally, perfusion can be an indirect measure of tissue metabolic activity because the normal vasculature adjusts perfusion to meet the metabolic demands of the tissue.
Perfusion is defined as the volume of blood that passes through a mass of tissue per unit time. Typical units for perfusion, or the essentially synonymous cerebral blood flow (CBF), are mL/100 g/min, and normal average blood flow to the adult brain is of the order of 40 to 60 mL/100 g/min (1). Because perfusion is a fundamental physiologic quantity, unlike T1 or even apparent diffusion coefficient, perfusion values should be unrelated to the technique used to measure them, and comparison of perfusion values obtained with many different imaging modalities is possible.
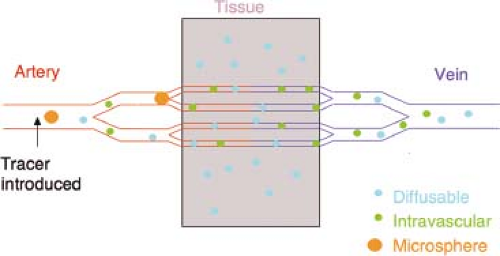
Because perfusion involves the transport of material through the tissue, all measurements of perfusion require a tracer quantity whose transport in the blood can be measured. For imaging purposes, the tracer must be observable using modern tomographic imaging techniques. Perfusion imaging was pioneered with nuclear medicine techniques using positron emission tomography (PET) and single photon emission computed tomography (SPECT) scanners and radioactive tracers. Today SPECT studies of CBF with 99mTc-hexamethylpropyleneamine oxime (HMPAO) and PET studies with H2O15 are still widely performed. Perfusion can also be measured using x-ray CT using either iodinated contrast agents (2) or stable Xe (3) as tracers. The most important distinctions among tracers, besides the techniques used for imaging them, are their diffusibility and their stability (Fig. 28.1). Diffusible tracers enter the tissue from the vasculature and eventually exit through the veins. Intravascular tracers cannot enter the tissue and remain in the vasculature throughout the entire experiment. A third class of tracers, typified by microspheres, remains trapped within the microvasculature or the tissue for an extended period of time. Many tracers, including radioactive isotopes, decay with time. The decay of tracers with time can add uncertainty to perfusion measurements, but it also allows for steady-state perfusion measurements, which are not possible with stable tracers.
Perfusion imaging with magnetic resonance imaging (MRI) is possible with many different tracers. Because unusual nuclear species are readily detected in the body with MRI, a number of investigations using fluorinated compounds (4,5,6), deuterated water (7), and O17 (8) have been performed. The recent development of hyperpolarized technology has also raised the possibility of perfusion measurement using hyperpolarized Xe gas (9) or hyperpolarized carbon-13 enriched liquids (10). Although all of these techniques are interesting and potentially promising, they lack the sensitivity of the proton MRI techniques usually employed for clinical studies. Over the last decade, two proton-based perfusion techniques have been developed (11,12,13,14) that have proven to be practical in the clinical setting and useful for diagnosis. The most widely used technique is known as bolus tracking because it involves the injection of a bolus of magnetic contrast agent while repeatedly imaging (15). It is usually performed using T2* or T2 contrast, in which case it is known as dynamic susceptibility contrast (DSC) MRI. Sometimes the T1 properties of the contrast agent are employed, and this technique is known as dynamic contrast enhancement (DCE) MRI. A less widely used but interesting alternative is the arterial spin labeling (ASL) (12) technique, which requires no exogenous contrast agents. In this technique, the spins in the inflowing arteries are perturbed with radiofrequency (RF) pulses, and the effect of these perturbed spins on image intensity after they flow into the slice is measured.
This chapter describes these two basic approaches and some of their limitations in the study of the brain. Applications of both techniques to the spine have been very limited. Because perfusion imaging has become a widely used tool for the study of neurologic disorders, specific applications of perfusion imaging are described in the disease-specific chapters.
DSC Contrast Imaging
Magnetic Contrast Agents in Neural Tissues
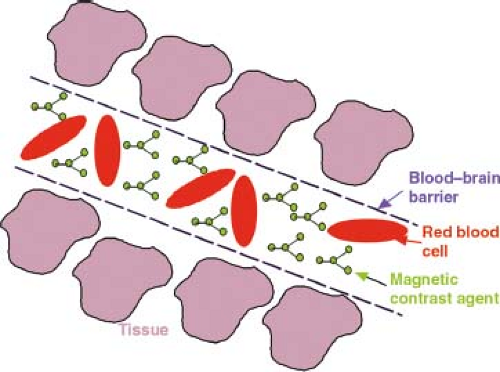
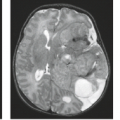
All available paramagnetic and superparamagnetic contrast agents are too large to cross the blood–brain barrier. Consequently all MR contrast agents are intravascular within normal brain tissue (Fig. 28.2). This differentiates brain perfusion studies from those in other tissues, where permeability is quite high. Because the brain–blood volume is between 3% and 6%, the possible signal changes resulting from alterations to the intravascular signal are relatively small. Fortunately, the presence of magnetic agents within the vasculature can have effects beyond the vessels (16,17,18,19,20,21).
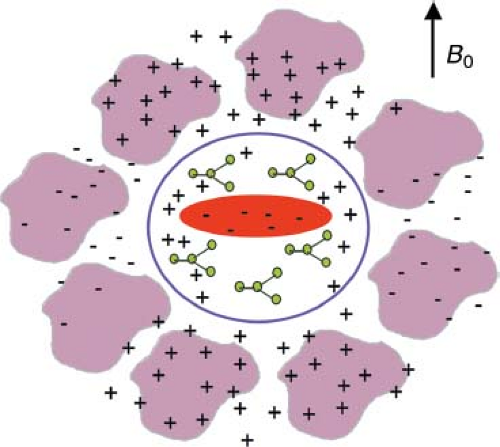
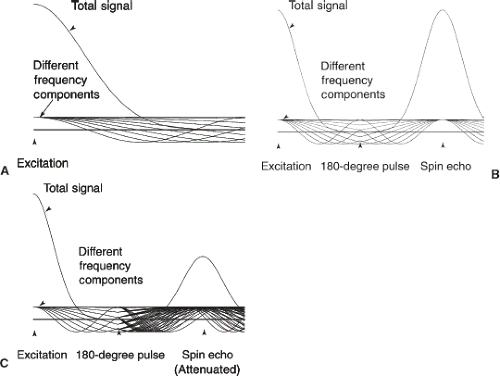
Magnetic contrast agents can act on spins outside of the vessels in two ways. First, spins can move between small blood vessels in the microvasculature and the tissue. Water molecules are in constant and rapid thermal motion. Frequent collisions with other water molecules, membranes, and large macromolecules prevent the molecules from moving very far. The random diffusive motion of these molecules does lead to slow movement. On the time scale of 100 ms, water can move in and out of a nearby capillary. Consequently, a larger volume than just the vascular volume can experience the effects of the contrast agent. The second, and more significant, way in which an intravascular contrast agent can affect tissue signal is by altering the magnetic fields in the nearby tissue. A strong magnet can have magnetic effects even at a considerable distance. Similarly, the presence of magnetic contrast agent in the blood vessels will cause nonuniform magnetic fields in the nearby tissue (Fig. 28.3). These nonuniform fields will cause a spread in the frequencies of tissue spins because frequency is proportional to magnetic field strength. After excitation, the spins will start to get out of phase, and the total signal will decrease. This decay of the signal is known as T2* decay, and the primary effect of the nonuniform fields is to decrease T2* (Fig. 28.4A).
Somewhat surprisingly, spin-echo T2 will also decrease when contrast agent is in the vessels. Although spin echoes are supposed to eliminate the effects of nonuniform magnetic fields, spin-echo refocusing is only successful when no motion is present (Fig. 28.4B). The contrast agent in small vessels causes large magnetic field gradients in the tissue that act like strong diffusion sensitizing gradients (see the chapter on diffusion MRI). When a long-TE image is acquired, these intrinsic gradients are “on” for the whole time, causing diffusion attenuation in the image (Fig. 28.4C). Note that T2 as measured by a fast spin-echo (FSE) sequence will not be as greatly changed because of the closely spaced refocusing pulses used in that sequence. This reduced sensitivity to T2 changes caused by an intravascular contrast agent in FSE is closely related to the reduced sensitivity to hemorrhage. The effect of contrast agent in large vessels on T2 of the surrounding tissue is very weak because the gradients produced depend on the size of the vessel. Consequently, it has been argued that T2-based DSC studies show less prominent large-vessel effects than T2* studies, for which the effect of the agent is independent of the vessel size. Large vessels are still very prominent on spin-echo DSC studies, however, probably because of intravascular T2 changes resulting from diffusion of water between red blood cells, which do not contain contrast agent, and the plasma, which does. Although it would seem that the diffusion rate in the tissue, which can be strongly affected in acute stroke, would have a large effect on the T2 with contrast agent present, clinical studies and theoretical investigations indicate that the effect of diffusion changes is small (18).
It is generally assumed (13,15,22) that T2 and T2* depend on contrast agent concentration according to the following relationships:
where C is the concentration of the contrast agent and R is the relaxivity of the agent. The T2 and T2* effects of a contrast agent are almost entirely determined by its magnetic susceptibility, that is, its tendency to enhance magnetic fields, and so the molecular chemistry of the agent is not critically important. On the other hand, the chemistry of the agent can have large effects on T1 and the permeability of a damaged blood–brain barrier to the agent. Typically, the T1 effects of the contrast agent are weak unless the agent passes through the capillaries into the tissue. If some leakage occurs, it may be desirable to have a small T1 effect (23), to minimize the impact of the leakage on the observed signal, or to have a strong T1 effect, so that it can be measured and removed computationally (24).
The Effect of a T2* or T2 Agent Bolus Injection
When contrast agent is present in high concentration in the vasculature, T2 and T2* are decreased relative to normal physiologic values. Smaller T2 or T2* means that the signal intensity on T2- and T2*-weighted images is decreased relative to normal. For neurologic applications, the contrast agent is usually injected as a rapid bolus, and images are acquired rapidly to monitor the signal change on time scales of 2 seconds or less (13,15,25). The advantages of a bolus injection are twofold. One advantage is that higher concentrations of contrast agent in the blood for a given dose can be achieved temporarily within a bolus than after the agent is mixed throughout the vasculature and tissues. A much larger signal change can be observed with these concentrations, making it easier to detect the effects of the contrast agent on the image. The second reason is that a time-varying concentration is necessary to infer perfusion from the signal change (13,22). Generally speaking, the bolus should be less spread out in time than the transit time through the tissue in order to most sensitively measure perfusion. Because such a tight bolus cannot be achieved with an intravenous injection, it is a general rule in MRI perfusion imaging that the tighter the bolus, the better (26).
One of the greatest challenges of DSC MRI is that the transit time through the tissue is so fast. The transit time through the vascular system in the brain is on the order of 4 seconds, a relatively short time. A similar time scale for transit is observed with iodinated contrast in CT. Consider instead the longer time scales in other types of perfusion measurements. When a diffusible tracer that enters the tissue is used, such as Xe used in stable Xe CT (3) or H215O used in PET flow imaging (1), the characteristic time to pass through the tissue is about 20 times longer because of the much larger accessible volume. Tc-HMPAO, a SPECT contrast agent used for flow sensitivity, enters the tissue and is chemically altered so it stays in the tissue even longer (27). Consequently, an MRI DSC perfusion imaging study requires a much tighter bolus and much higher temporal resolution imaging to measure perfusion than a study with a diffusible tracer. On the other hand, the entire MRI perfusion experiment can be performed in a much shorter time than one with diffusible tracers.
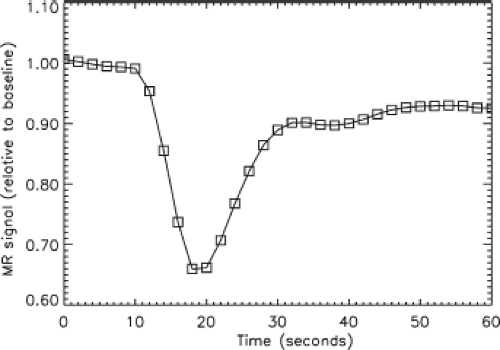
An example of the signal from a region of interest (ROI) during a DSC perfusion imaging study is shown in Figure 28.5. Notice that the images are acquired once every 1.5 seconds, as is necessary when measuring such a short transit through the tissue. Prior to the contrast arrival, the image intensity is stable, but once the agent starts to enter the vasculature of the tissue, the signal intensity drops rapidly. Depending on the contrast agent used, the sequence parameters, and the volume of the blood vessels in the tissue, the signal intensity can drop by from a few percent to more than a factor of two. Eventually the signal rises again after the bolus washes through the tissue, but usually before the signal can recover to zero, the bolus returns after circulating through the heart and lungs again. This second
bolus is strongly attenuated because of further spreading of the bolus as well as absorption into the permeable tissues outside of the brain. Usually a third recirculation is hard to detect, but the image intensity never fully returns to the original intensity because the arterial concentration of contrast agent remains significant for many minutes after the injection (28). With the new class of blood pool agents (29), the recirculation may need to be better understood because the arterial concentration will remain higher than with agents that are absorbed elsewhere in the body.
bolus is strongly attenuated because of further spreading of the bolus as well as absorption into the permeable tissues outside of the brain. Usually a third recirculation is hard to detect, but the image intensity never fully returns to the original intensity because the arterial concentration of contrast agent remains significant for many minutes after the injection (28). With the new class of blood pool agents (29), the recirculation may need to be better understood because the arterial concentration will remain higher than with agents that are absorbed elsewhere in the body.
The curve in Figure 28.5 has information on perfusion, blood volume, and transit time through the tissue. Extracting this information, either in quantitative or qualitative form, from the image time series is challenging. A number of simple approaches as well as complex algorithms have been proposed. The approaches are most clearly divided by the objectives. Qualitative techniques are usually designed to provide useful diagnostic contrast with a minimum of image postprocessing steps. Quantitative techniques are targeted at obtaining absolute or at least relative measures of blood flow, blood volume, or tissue mean transit time (MTT). Because quantification methods may increase processing time, noise, and motion sensitivity, it is not necessarily true that they will provide greater diagnostic accuracy. However, it seems likely that separating intrinsic tissue parameters such as perfusion from extrinsic variables such as bolus width, contrast dose, and upstream vascular transit delays will lead to increased diagnostic accuracy.
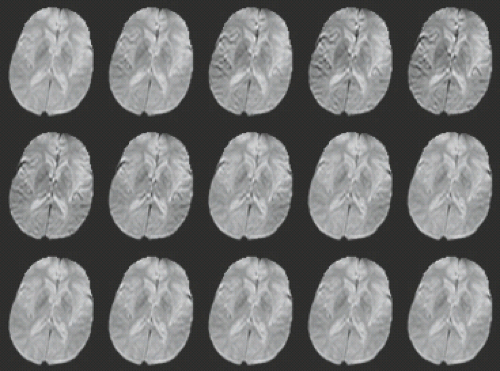
The simplest way to observe perfusion-related changes is visually to inspect the image time series at a sharp window level so as to clearly see changes in image intensity. This is most effective with strong signal changes such as in gradient-echo T2* scans or spin-echo T2 changes with a high dose of contrast agent. Because this viewing of the images can be performed without any postprocessing, it is sometimes the only approach available. The transit of the bolus and regional variations of the bolus arrival can usually be clearly seen (Fig. 28.6). One of the greatest advantages of such an analysis is that this visual inspection can be performed even in the presence of severe patient motion. Because the underlying images are often motion-insensitive snapshot echo-planar images, each snapshot will be of good quality even if the patient is moving rapidly. A single image near the peak of the bolus in normal tissue can be used to identify regions with late or nonexistent contrast arrival. Such inspection of individual images is always an option when further postprocessing of the data is hopelessly corrupted by subject motion.
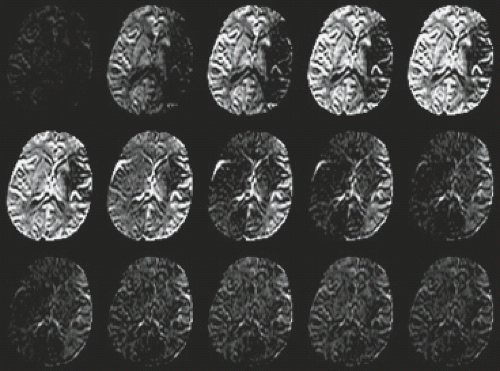 FIGURE 28.7 The same series of images as in Figure 28.6, except that each image is subtracted from the first image in the series. With the subtraction, the effects of the inflow of the contrast agent are more readily apparent. |
If patient motion is not a major issue, then the effects of contrast agent passage can be accentuated by subtracting each image from an image acquired before the contrast bolus arrives. For the best signal-to-noise ratio, it is preferable to use an average of several images acquired before the bolus arrival for the subtraction. An example of such a subtraction is shown in Figure 28.7. Now baseline image intensity is not observed, and all the intensity in the image is a result of the flow of contrast into the imaged region. Any unperfused region will show no signal intensity in the subtraction image. Thus these images are a measure of perfusion mixed with a number of other contrasts. In the example of Figure 28.7, a marked asymmetry is apparent that is an indication of a stroke in this patient. Late arrival of contrast in still-perfused regions of the affected middle cerebral artery distribution is an indication of abnormal hemodynamics. As discussed later, the late arrival of contrast agent can mean low perfusion, high blood volume, or delayed arrival of the agent due to a slow or circuitous arterial supply. In this patient, in whom motion is minimal, the subtraction adds markedly to the conspicuity of hemodynamic abnormalities. However, it does require the viewing of multiple images for each slice. Much of the information can be derived from just a few images, such as the image when contrast fully enters normal tissue, image number 5, and a later image to show later arrival in some regions, image number 8. However, unusual bolus width or timing or unusual hemodynamics can complicate the interpretation of this smaller set of images. For this reason, numerical calculations are often performed to provide better summaries of the data.
A very popular summary of bolus passage data is the time-to-peak concentration (TTP) map (30). This is a map that provides a clean measure of the arrival time of the bolus in the tissue and can be a clear indicator of some abnormalities. When the concentration is at a maximum in a region of tissue, the signal intensity is at a minimum. The TTP is calculated one pixel at a time by searching through all of the signal intensities as a function of time for that pixel. The minimum signal intensity is found, and the time corresponding to that minimum intensity is stored as the TTP. There are some problems with TTP maps. First, the limited temporal resolution of most acquisitions means that the TTP values are measured in discrete values of 1 to 2 seconds. Because a typical range of TTP for normal tissue is less than 5 seconds, the TTP map cannot detect subtle changes. This problem can be largely eliminated by interpolating the data between the obtained time points or by fitting the signal intensity to a model. A second problem with TTP maps is ambiguity in the TTP in regions where the concentration
is very low such that the minimum signal intensity is mostly a result of noise. This can occur in regions with very low flow, such as in the core of a stroke (31). Because a larger TTP is a sign of abnormality and so is very low concentration, it is natural to assign an arbitrarily large value to the TTP map in regions where the effect of the bolus is very small. Examples of this type of problem and its solution are shown in Figure 28.8.
is very low such that the minimum signal intensity is mostly a result of noise. This can occur in regions with very low flow, such as in the core of a stroke (31). Because a larger TTP is a sign of abnormality and so is very low concentration, it is natural to assign an arbitrarily large value to the TTP map in regions where the effect of the bolus is very small. Examples of this type of problem and its solution are shown in Figure 28.8.
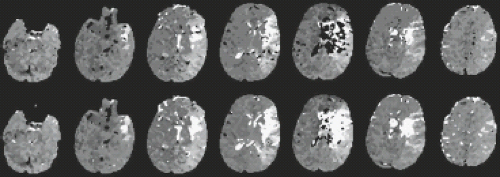 FIGURE 28.8 Time-to-peak images calculated from the bolus study of Figures 28.6 and 28.7. True time-to-peak maps (top) show noisy, patchy intensity in the core of the ischemic region because little or no contrast agent enters this region. A thresholding approach that substitutes a high value in regions with very low signal change (bottom row) can improve image appearance and highlight the location of greatest pathology. |
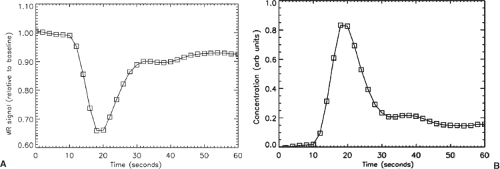
The TTP map is a popular measure of the delayed arrival of contrast, but it does not indicate the amount of contrast agent that moves through the tissue. A second map, which is relatively easy to calculate, is the area under the concentration versus time curve. As will be explained, this area is proportional to the volume of blood within a voxel, so maps of the area are consequently called cerebral blood volume (CBV) maps. To generate such a map, the signal intensities must first be converted into relative concentrations. This requires taking the logarithm of the signal intensity, S, divided by the baseline signal intensity, S0:
An example of signal intensity curve and the corresponding concentration–time curve are shown in Figure 28.9. The area under the curve, also known as the discrete integral of the curve, is then calculated pixel by pixel. Calculation of the CBV in this manner is very susceptible to motion-related noise. Suppose that after the bolus injection, the patient moves slightly, causing the intensity in the pixel to decrease relative to baseline. The calculation of the area will be dramatically increased by the small shift because it keeps adding area for as long as data are being obtained. Even in the absence of motion, the signal intensity will usually not return to zero because it takes hours for the concentration of contrast agent in the blood to vanish completely. For these reasons, the calculation of the area is usually stopped at a time shortly after the bolus peak.
More elaborate image processing than calculating TTP and CBV maps is usually only performed if quantification of perfusion or the tissue MTT is desired. To explain how this quantification is performed, it is necessary to first review some of the theory of tracer kinetics (2,22,32). This theory provides the methods necessary for calculating perfusion and MTT as well as the justification for the relationship between the area under the concentration–time curve and CBV.
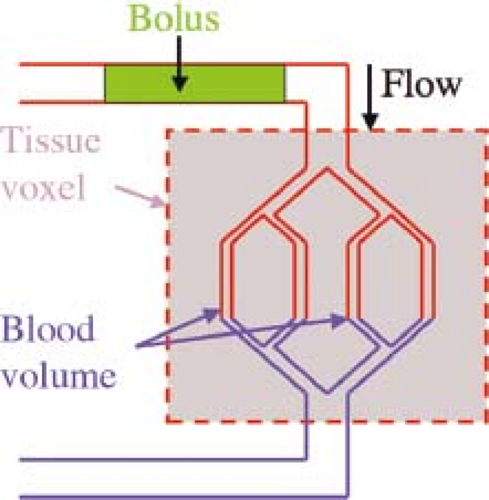
A schematic drawing of the DSC imaging experiment for 1 cm3 of an image is shown in Figure 28.10. The tissue in the cube has a density ρ, and the volume of all the blood vessels in the cube is V. One or more arteries provide a flow into the cube of F milliliters per second, and an equal flow is carried out by the veins. To simplify the experiment, consider a very narrow square bolus of concentration Cf and duration t injected just upstream of the feeding arteries.
Shortly after the bolus is injected, it flows into the cube of tissue through the arteries. The blood in the vessels now contains a mass of contrast agent. Immediately after the contrast flows into the cube of tissue, clean blood will flow in through the arteries and blood mixed with contrast agent will flow out the veins. This outflow of contrast agent in the venous blood will
start to clear the blood in the vessels. If we used the MRI signal to monitor the concentration of contrast agent in the tissue, we would measure a gradual decrease in the concentration. If we assume that the contrast agent mixes quickly in the vasculature, the concentration will actually decrease exponentially with time. Exponential decay should be familiar from experience with T2 decay, another exponential process in MRI. Instead of T2, however, the characteristic time for clearing the blood is called the MTT. The MTT is determined by the rate at which blood flows in, F, and the volume of the blood, V, according to the formula MTT = V/F. The MTT is also the time it takes for a volume of blood V to enter the cube if the flow is F. It makes intuitive sense that the replacement of the whole volume of the vasculature with fresh blood will clear the contrast agent from the cube of tissue. In some ways, MTT is a refined version of the TTP previously discussed, but it is not identical to it.
start to clear the blood in the vessels. If we used the MRI signal to monitor the concentration of contrast agent in the tissue, we would measure a gradual decrease in the concentration. If we assume that the contrast agent mixes quickly in the vasculature, the concentration will actually decrease exponentially with time. Exponential decay should be familiar from experience with T2 decay, another exponential process in MRI. Instead of T2, however, the characteristic time for clearing the blood is called the MTT. The MTT is determined by the rate at which blood flows in, F, and the volume of the blood, V, according to the formula MTT = V/F. The MTT is also the time it takes for a volume of blood V to enter the cube if the flow is F. It makes intuitive sense that the replacement of the whole volume of the vasculature with fresh blood will clear the contrast agent from the cube of tissue. In some ways, MTT is a refined version of the TTP previously discussed, but it is not identical to it.
Suppose the concentration of contrast agent in the feeding arteries is a very short, square bolus of concentration Cf and duration τ. Discussion of how the arterial concentration can be measured with MRI is reserved for the next section. The total mass of contrast agent that flows into the tissue, Ct (t = 0), is given by Cf × τ × F. This makes intuitive sense because higher concentration, longer bolus duration, or higher flow will put more contrast agent into the tissue. We can solve this equation for flow,
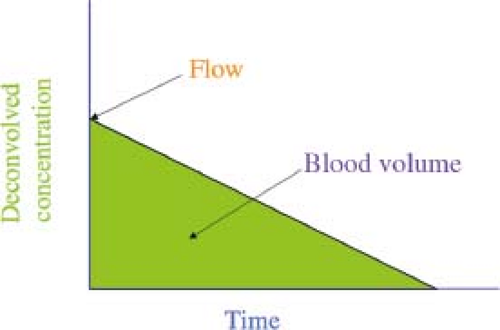
Similarly, we can calculate the volume, V, from the area under the concentration–time curve. A description of this area calculation is shown in Figure 28.11. Mathematically, the concentration as a function of time is given by
and the area under the curve is given by
The area under the curve is directly proportional to the blood volume. Once the blood volume and flow are determined, the MTT can be obtained just by taking the ratio. One of the advantages of calculating the blood volume from the area under the concentration–time curve is that the area is the same regardless of how wide the bolus is. The same is not true for the flow, F. If we had slowly injected the contrast agent over a time as long as or longer than the MTT, then the formula for flow would not be accurate (Fig. 28.12). It is for this reason that CBV is arguably the easiest quantity to calculate from the DSC experiment.
In general, the exponential clearance shown in the foregoing equation is not an accurate description of the time behavior of the clearance when an intravascular contrast agent is used (32). Although the mathematics of nonexponential clearance is more involved, the approach to quantification described previously is not changed. However, in the nonexponential clearance case, the MTT cannot be calculated from the first moment of the deconvolved tissue concentration curve.
Measurement of the Arterial Concentration
As indicated previously, it is not possible to measure perfusion with DSC imaging without a separate measure of the arterial concentration. Because arterial sampling would greatly increase the invasiveness and complication of the study, the arterial concentration is usually estimated noninvasively using MR images. The concentration of the contrast agent can be inferred from its effect on either T2, T2*, or T1 (13,22) or the frequency of the MR signal (33) in or near a large vessel. Often the same images used for measuring the tissue contain a major artery whose signal can be measured by placing a ROI on the vessel. The signal intensity in the ROI as a function of time can thus be measured, and, if a theory for the relationship between signal intensity and concentration is available, then the concentration in the feeding arteries as a function of time can be known. This concept is shown schematically in Figure 28.13.
Although this basic approach can be used, it may provide a poor or inaccurate measure of the contrast agent concentration. One problem, which can occur especially in T2*- or T1-weighted images, is insensitivity at high concentrations. On longer–echo time (TE) gradient-echo images, the contrast agent can cause almost complete attenuation of the signal from a voxel with a large vessel. When the attenuation is very high, small inaccuracies in the signal, such as noise or motion, will cause large errors in the measured concentration. Similarly, in T1-weighted imaging, high concentrations of contrast agent in the blood can cause T1 to be so short that full recovery of the magnetization occurs between each repetition time (TR), making it difficult to measure T1.
Another potential limitation to using an ROI over a vessel is that the images used to monitor concentration in the tissue can be of mixed contrast. Frequently, T2*-weighted images are obtained every 1 to 2 seconds during a DSC contrast scan. With such a short TR, the images have both T1 and T2* weighting. The signal intensity in a large vessel will change because of both T1 and T2* effects. Another challenge with this approach may be uncertainty in the relationship between contrast agent concentration and T2 or T2*. This problem is perhaps greatest in spin-echo images. The extravascular signal loss with spin echo is a result of diffusion around small vessels in the tissue. A large vessel should have only very small effects due to diffusion in and out of the vessel. Much of the signal attenuation observed in large vessels is due to diffusion of water molecules between red blood cells, which do not contain magnetic contrast agent, and the plasma, which does. This is an intravascular effect only, and so a different relationship between contrast concentration and T2 is necessary for large vessels than for tissue. Simulations (34) and measurements (35) suggest that the relationship between concentration and 1/T2 is not linear and may depend on the size and angle of the artery. In addition, the signal attenuation in a voxel containing a large vessel will depend on both the concentration of the agent in the artery and the fractional volume of the contrast agent. Although some limited work in animals has shown agreement between T2 measurement in ROIs near, but not in, arteries and contrast agent concentration (13), arterial input function measurement based on T2 clearly deserves further attention. T2* measurements in large vessels can also depend on vessel orientation relative to the main magnetic field.
Many of the problems that occur with measuring arterial concentration stem from using the same images for tissue and arterial measurement. If additional images are obtained, a number of significant improvements are possible (36). One of the simplest schemes is a dual echo experiment, which obtains each of the slices twice after excitation. The shorter-TE image is less attenuated by contrast agent concentration, and so it can be more sensitive for measuring arterial contrast agent concentration, whereas the longer-TE image is ideal for tissue concentration measurement. This dual echo approach has the added advantage that the effects of T1 can be separated from the effects of T2* (24,37,38,39). The ratio of the signal in the short- and long-TE images depends only on T2*. Another scheme is to measure the frequency change that occurs in a vessel containing contrast agent (32). The frequency change is very linear with contrast concentration, and thus many of the problems of T2 and T2* intensity models are avoid. However, frequency is usually measured by observing the phase of the voxel on a longer-TE image. Flowing blood can also have phase shifts from motion in the presence of gradients, and these phase shifts could cause excess noise or systematic errors.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree