From Image Formation to Image Contrast: Understanding Contrast Mechanisms, Acquisition Strategies, and Artifacts
Sean C.L. Deoni
One of the great advantages of magnetic resonance imaging is its extreme versatility in investigating tissue structure, composition, and function. This flexibility stems from the ability to sensitize the MRI signal to an extensive and diverse array of structural properties, metabolic or chemical attributes, and physiologic processes through relatively subtle adjustments in acquisition strategy. Perhaps the most direct clinical illustration of this flexibility is the ability to generate an unparalleled degree and range of contrast between tissues, which lends the method ideally to the task of detecting disease and pathology. The contrast generated in an MR image depends not only on the intrinsic MR properties of tissue, such as the longitudinal and transverse relaxation times (T1 and T2) and proton density (PD) (which each are related to the microstructural, biophysical, and biochemical characteristics of the tissue), but also on the acquisition strategy (i.e., pulse sequence and acquisition parameters), imaging hardware (e.g., field strength and radiofrequency [RF] coil geometry), and image reconstruction methodology. Throughout clinical MRI protocols, the acquired signal is typically weighted toward one or more of these intrinsic properties in order to produce a desired contrast between tissues. However, it is important to appreciate that while the obtained contrast may be primarily related to T1 differences—for example, in a T1 weighted image—it remains a complex function of each of the listed effects, and modulated by patient positioning and coil loading. The choice of contrast mechanism (T1, T2, diffusion, etc.), pulse sequence, and acquisition parameters may mask subtle tissue alteration, and challenge the direct interpretation of signal changes within or between tissues. Further, errors or artifacts introduced by the choice of reconstruction methodology may further impair clinical interpretation, or obscure subtle alteration. The goal of this chapter is to provide an abbreviated overview of MR signal contrast mechanisms, acquisition strategies, and reconstruction approaches relevant to radiologists. We aim to provide a foundation for understanding the biophysical basis of the MRI signal, how contrast may be manipulated through acquisition, and what artifacts may be introduced through the imaging process.
Part I: Fundamentals of Image Data Acquisition
Acquiring a 2D Image
Three central concepts are fundamental to generating an image by MRI: (1) The raw signal acquired in an MRI experiment corresponds to the two-dimensional (2D) or three-dimensional (3D) Fourier transform of the object being imaged; (2) The use of magnetic field gradients define a trajectory through the acquired Fourier transform (also termed “k-space”); and (3) The object image is obtained by calculating the inverse Fourier transform on the acquired k-space data.
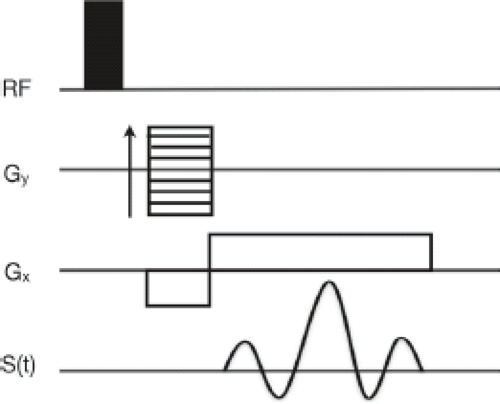
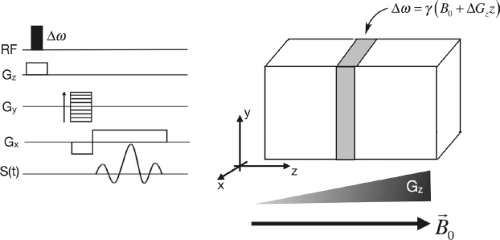
In MRI nomenclature, the temporal or spatial domain of data points is denoted “image space,” and their corresponding frequency domains as “k-space.” The most common approach to acquiring 2D k-space data is line-by-line, in a raster pattern. To better understand the relationship between the applied frequency and phase-encoding gradients, and the corresponding position in k-space, it is helpful to introduce an imaging sequence timing diagram (Fig. 2.1), which provides a graphical illustration of an acquisition sequence.
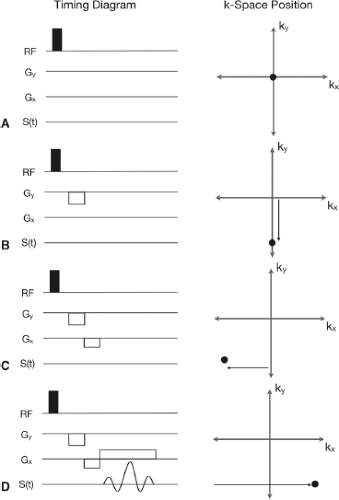
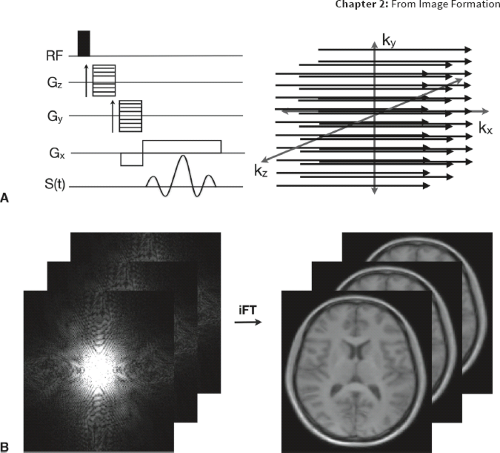
The relationship between the sequence diagram and k-space position is shown in Figure 2.2. Recall that the position in k-space is related to the strength of the linear field gradient, and the length of time it is applied.
The gradients act to move our position through k-space, with phase encoding used to select the ky position, and frequency encoding used to select the kx position. During the application of the positive frequency-encoding gradient (Fig. 2.2), the signal is sampled at uniform timing increments, acquiring each kx
point along the selected ky line. This process is then repeated N times, with the Gy amplitude uniformly altered to acquire N ky lines (Fig. 2.3A) and fill in the complete k-space. Once the desired k-space has been acquired, the 2D inverse FT is calculated to recover the image (Fig. 2.3B).
point along the selected ky line. This process is then repeated N times, with the Gy amplitude uniformly altered to acquire N ky lines (Fig. 2.3A) and fill in the complete k-space. Once the desired k-space has been acquired, the 2D inverse FT is calculated to recover the image (Fig. 2.3B).
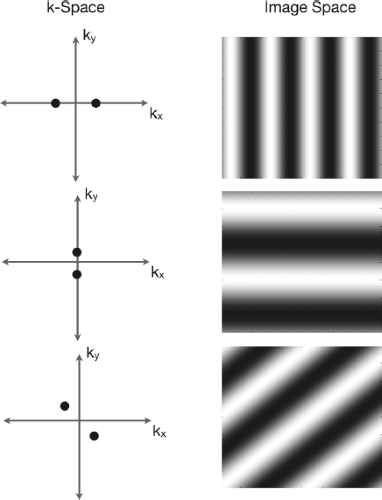
The 2D k-space can be considered a look-up table of the spatial frequencies that make up the image. Each point within k-space (kx,ky) corresponds to a particular spatial frequency oriented at the same angle as the angle of the line from (kx,ky) through the origin (Fig. 2.4).
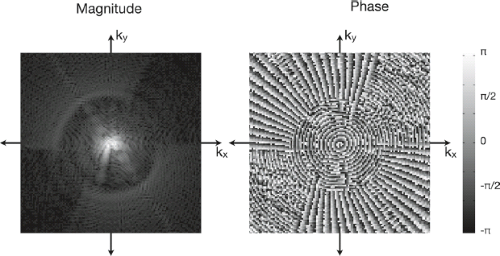
Further, recall that the acquired signal is complex; that is, it has both a “real” and “imaging” component as provided by quadrature detection. Thus, k-space is also complex (Fig. 2.5). The real (Re) and imaginary (Im) components can be combined into magnitude (|S|) and phase (q(S)) values at each point, as
and
The magnitude of each k-space point is the amplitude of the corresponding spatial frequency wave, and the phase is its phase shift. For example, if all spatial frequencies correspond to 2D cosine waves, a point with phase = π/2 would be a sine wave.
From 2D to 3D Acquisitions
Acquisition of 3D images can be accomplished in one of two ways: multi-slice 2D imaging, or true 3D imaging. Multi-slice
imaging, as the name suggests, involves the acquisition of multiple 2D images (slices) arranged in a stack so as to cover a 3D volume. To perform multi-slice imaging, the RF excitation portion of the imaging sequence is modified so that only the desired slice is excited. Once this is achieved, 2D FT imaging is used to acquire the FT of the slice. The process is then repeated, with the excited slice moved along the object. To make the excitation spatially selective, we again exploit the relationship linking magnetic field strength and precessional frequency, as well as the requirement that an RF pulse must be applied at the precessional frequency in order to tip the net magnetization. Here, a linear gradient is applied along the z axis of the object, Gz, inducing a dispersion of precessional frequencies in this direction. Application of a band-limited RF pulse (i.e., an RF pulse containing a specific range of frequencies) at the same time as Gz result in only the magnetization from a specific region of the object being tipped into the transverse plane (Fig. 2.6).
imaging, as the name suggests, involves the acquisition of multiple 2D images (slices) arranged in a stack so as to cover a 3D volume. To perform multi-slice imaging, the RF excitation portion of the imaging sequence is modified so that only the desired slice is excited. Once this is achieved, 2D FT imaging is used to acquire the FT of the slice. The process is then repeated, with the excited slice moved along the object. To make the excitation spatially selective, we again exploit the relationship linking magnetic field strength and precessional frequency, as well as the requirement that an RF pulse must be applied at the precessional frequency in order to tip the net magnetization. Here, a linear gradient is applied along the z axis of the object, Gz, inducing a dispersion of precessional frequencies in this direction. Application of a band-limited RF pulse (i.e., an RF pulse containing a specific range of frequencies) at the same time as Gz result in only the magnetization from a specific region of the object being tipped into the transverse plane (Fig. 2.6).
An alternative to multi-slice imaging is fully 3D imaging using phase encoding along the third dimension. In 3D imaging, a volume-selective RF pulse excites spins throughout the entire object, and then the object’s 3D k-space is acquired analogously to the 2D case. The Gz gradient acts as an additional phase-encoding gradient, so that the phase of the signal is related to both Gy and Gz,
and the received signal is
Again, we can write γ Gzt as kz(t), where
Just as the duration and strength of Gx and Gy defined our (kx,ky) position in the 2D FT (Fig. 2.2), the duration and strength of Gx, Gy, and Gz now define a point (kx,ky,kz) in the 3D FT. The 3D FT is acquired as with the 2D case, with the phase-encoding gradients (Gy and Gz) used to define a line in k-space, and the frequency-encoding gradient (Gx) used to sample that line. This process is then repeated, with Gy and Gz uniformly incremented (Fig. 2.7A). Finally, a 3D inverse FT is calculated to reconstruct the object’s image (Fig. 2.7B).
The primary advantages of 3D over multi-slice acquisitions relate to spatial resolution and image quality. To achieve high resolution in the through-plane (z) direction, “narrow” RF pulses (i.e., pulses containing a small range of frequencies) and a strong Gz gradient are required. In contrast, high-resolution 3D acquisitions can be acquired simply by collecting higher frequency k-space data. An improvement in image quality is also obtained through an increase in the signal-to-noise ratio (SNR), a common metric used to quantify the degree of noise within an image. In simple terms, SNR refers to the “graininess” of image (Fig. 2.8), and is calculated as the ratio of the signal within the object of interest to the background noise,
where [s with bar above] is the mean signal calculated from a desired region of interest (ROI), and σS is the standard deviation of the signal in a background ROI. If the background noise is gaussian (as is typically the case), a common approach to increasing SNR is by averaging a set of replicate measures (i.e., signal averaging). This increases the SNR by the square root of the number of averaged measurements. Though not obvious, acquisition of a 3D image over 2D multi-slice volume has the same effect as signal averaging, with SNR increasing as
where nkz is the number of kz phase-encoding “slices” in the 3D image, and SNR2D is the SNR for the 2D multi-slice acquisition covering the same volume. As can be seen, significant improvements in SNR can be realized through fully 3D imaging.
Before moving on, a note about gradient nomenclature is in order. We have defined Gx as the frequency-encoding gradient, and Gy and Gz as phase-encoding gradients. In reality, any dimension may be chosen for frequency encoding.
Important Properties of k-Space
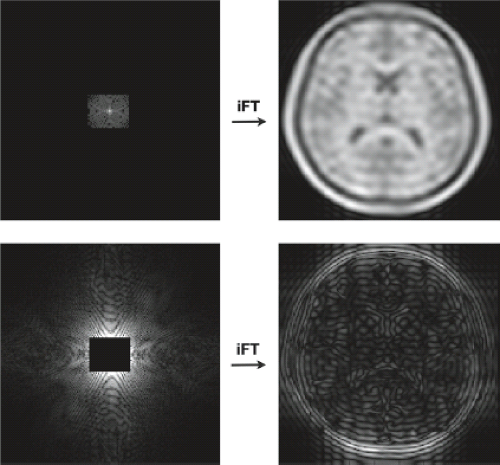
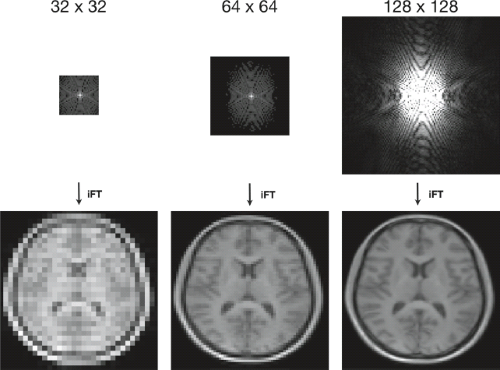
Since k-space plays such a central role in MRI, it is worth detailing some of its properties that relate to image quality and potential artifacts. The first of these is the relationship between k-space extent and image information content. Briefly, the low-frequency center of k-space contains most of the image content (i.e., structure and contrast), whilst the high-frequency outer portion of k-space contains the image detail (Fig. 2.8). Thus, acquisition of higher-frequency data in k-space results in increased detail in the final image (Fig. 2.9). However, this carries the potential dual penalties of increased scan time and decreased image SNR.
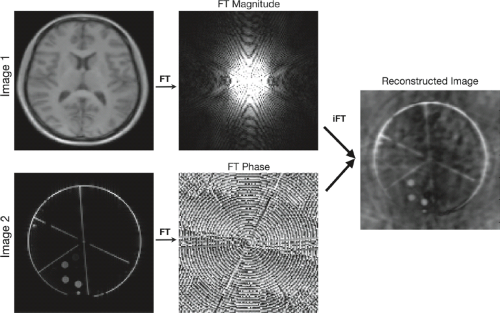
The second important point about k-space is that phase information is important. This is best illustrated through the following example (Fig. 2.10) in which the FTs of two images were calculated and the inverse FT performed using the magnitude from image 1 and the phase from image 2. As can be seen, the resultant image more closely resembles image 2. Therefore,
it is critical that processes that alter the phase from its true value be avoided or minimized. A quick examination of Table 2.1 reveals one particularly troublesome process: motion! By the shift theorem, motion of the object results in a phase shift in the FT. We will examine this in greater detail in the following section.
it is critical that processes that alter the phase from its true value be avoided or minimized. A quick examination of Table 2.1 reveals one particularly troublesome process: motion! By the shift theorem, motion of the object results in a phase shift in the FT. We will examine this in greater detail in the following section.
Alternate k-Space Trajectories
While the Cartesian–raster pattern sampling approach remains the most common in practice, there is a practically infinite number of potential alternative trajectories with which to acquire k-space. Using the basic principles described in the preceding
section it is possible to imagine any gradient trajectory that can be used for imaging. To expand on our prior discussion, we will briefly detail three of the more commonly used alternative trajectories: radial, echo-planar, and spiral.
section it is possible to imagine any gradient trajectory that can be used for imaging. To expand on our prior discussion, we will briefly detail three of the more commonly used alternative trajectories: radial, echo-planar, and spiral.
TABLE 2.1 Some Useful Fourier Relationships and Properties that Are Relevant to MRI | |
|---|---|
|
Radial Sampling: Radial sampling of k-space (Fig. 2.11) was one of the earliest approaches to MRI, though reconstruction was conventionally performed using filtered back projection rather than Fourier inversion. The primary advantages of a radial sampling approach include the following: (1) The short time between excitation and sampling the center of k-space, which can be useful when imaging tissues or objects with short T2 relaxation times; and (2) Its differential sensitivity to motion compared to Cartesian trajectories. The main disadvantage of the strategy is the variable density with which k-space is sampled. In order to sample the periphery of k-space sufficiently to avoid aliasing, the centre of k-space is vastly oversampled. Thus, the approach is less time efficient than a Cartesian trajectory.
Echo-Planar Imaging (EPI): EPI represents a direct extension of the line-by-line Cartesian trajectory we are well familiar with. The primary advantage of EPI is that an entire plane of k-space can be acquired after a single excitation pulse (Fig. 2.12), facilitating a significant reduction in imaging time. Typical acquisition times may be as short as 40 milliseconds, allowing motion to be “frozen.” Following the RF pulse, an initial Gy gradient is used to move to the starting point on the ky axis. A low-amplitude Gy gradient is then combined with an oscillating Gx gradient to produce a sinusoidal trajectory across the slice. Because the readout gradient sweeps back and forth k-space in alternating directions there can be misalignment in the signal amplitudes for every other line (i.e., a phase shift). This can result in a blurred image or a subtle offset ghost image in the reconstructed image. The effect of structured and random phase shifts on image quality will be discussed later in this chapter as part of the effects of motion. An additional confound with EPI is the decay of the magnetization during the readout. As will be seen later, the transverse magnetization typically decays with a time constant on the order of tens of milliseconds, requiring the image to be acquired very rapidly.
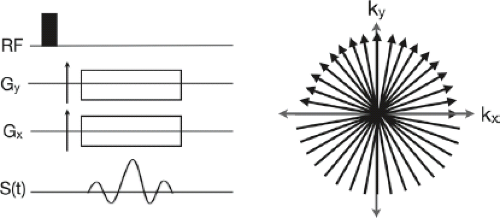 FIGURE 2.11 Pulse sequence diagram and k-space trajectory associated with a 2D radial sampling strategy. |
Due to its speed and resilience to motion, EPI is used in several neuroscience applications, including functional and diffusion imaging.
Spiral Acquisition: Spiral acquisition strategies (Fig. 2.13) offer an alternative to EPI trajectories. These maintain some of the speed advantages of EPI, while placing reduced demand on the gradient systems since it is not necessary to reverse the gradient direction with each line of k-space. Since the center of k-space is acquired immediately following excitation, spiral acquisitions are particularly well suited to imaging tissues whose signals decay quickly. Further, like radial acquisitions, spiral trajectories are less sensitive to motion effects. However, the primary disadvantages of spirals are variable sampling density in the center versus the periphery of k-space, and the sensitivity to gradient nonlinearities. If the gradient waveforms are not performed ideally, there will be mismatch between where one thinks they are in k-space and where they actually are. This can lead to errors in k-space filling, which result in image quality degradation and artifacts.
Spatial Resolution, Field of View, and Artifacts
As Figures 2.8 and 2.9 suggest, the region and extent of the acquired 2D or 3D k-space can significantly impact the quality and detail of the reconstructed image. In addition to these basic aspects, the sampling rate also plays an important role. The
Fourier relationship that links the acquired “raw” k-space data to the final image introduces an additional confound when discussing signal sampling and other aspects of image acquisition, for while we view the results in image space, we must consider what has occurred in k-space.
Fourier relationship that links the acquired “raw” k-space data to the final image introduces an additional confound when discussing signal sampling and other aspects of image acquisition, for while we view the results in image space, we must consider what has occurred in k-space.
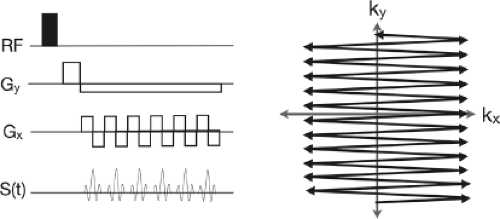 FIGURE 2.12 Pulse sequence diagram and k-space trajectory associated with a 2D gradient echo planar imaging sequence. |
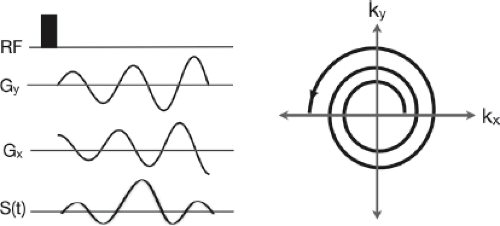 FIGURE 2.13 Pulse sequence diagram and k-space trajectory associated with a 2D spiral sampling strategy. |
Sampling
While frequency-encoding or readout gradient is turned on, we are also sampling the continuous MR signal, S(t), as discrete measurements separated by a uniform time increment, Δt. Sampling is performed using an analog-to-digital converter (ADC), which converts the continuous sinusoidal voltage signal from the RF coil into a digital value that reflects the signal’s amplitude. The primary goal of the sampling process is to obtain a set of measurements that faithfully characterizes the original signal, allowing its accurate reconstruction.
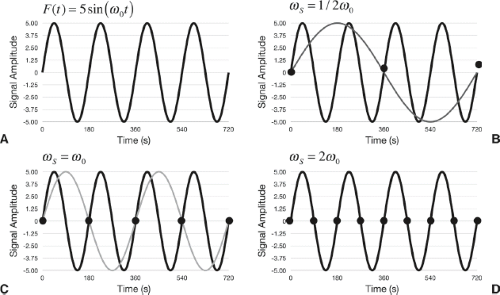
As a simple example, consider the need to sample a sinusoid F(t) with frequency ω0 (Fig. 2.14). Perhaps ideally, we would acquire as many samples of F(t) as possible. However, this would place significant burdens on the ADC, as well as require substantial memory to digitally store all the samples. A more practical and pragmatic approach is to determine how few samples of F(t) are needed to faithfully reconstruct it. We can see from Figure 2.14 that if the sampling rate (ωs) is less than 2ω0 we can represent F(t) with a lower-frequency sinusoid. This effect is called aliasing, that is, the high-frequency signal is aliased by a lower-frequency signal. A real-world example of aliasing is the television video of a car wheel spinning. As the car speeds up, the tire’s rotation appears to speed up, then stop, then reverse, stop, speed up again, and so on. Obviously, the tire is not reversing whilst the car is traveling forward. The tire’s whacky behavior is a result of aliasing. The condition that ωs should be greater than, or equal to, 2ω0 is termed the Nyquist–Shannon sampling theorem (1), with the Nyquist sampling rate being the minimum rate that satisfies the theorem.
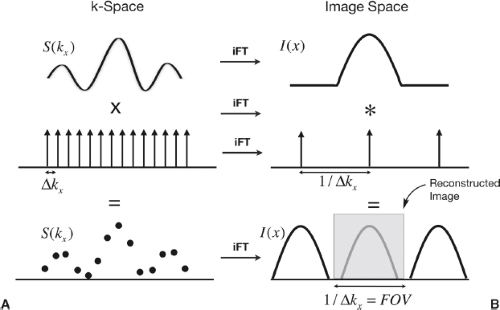
Mathematically, we can describe sampling as the multiplication of the continuous signal by a Dirac comb function, which is a series of impulse functions at regularly spaced intervals, t (Fig. 2.15). It is important to recall that in MRI, the signal acquired is not of the object itself, but rather the FT of the object. Therefore, it is useful to consider the sampling process not in the image domain, but in k-space (Fig. 2.16A), where each sample is a measurement of the object’s Fourier transform, and the temporal step between samples corresponds to an increment in spatial frequency, Δkx,
We can examine the relationship between k-space and image space sampling through the Fourier relationship of each step (making use of Fig. 2.15 and Table 2.1). The multiplication of the continuous FT by a Dirac comb function with spacing Δkx in k-space corresponds to the convolution the object’s image with a Dirac comb function with spacing 1/Δkx (Fig. 2.16B) in image space. The result of this convolution is a set of images that repeat with spacing 1/Δkx. A rectangular window of width 1/Δkx centered about the origin corresponds to the reconstructed image area. The number of points in the reconstructed image (also termed pixels, or picture elements) is equal to the number of samples acquired in k-space, Nx, and 1/Δkx is the image field of view in x (FOVx). Therefore, the spatial resolution of the image is equal to FOVx/Nx. Typical values for Nx and FOVx for brain imaging 256 and 25 cm, respectively, result in an image spatial resolution of approximately 1 mm.
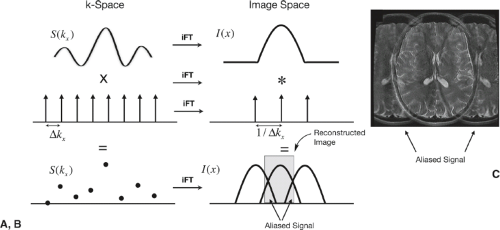
With an appreciation of the relationship between sampling in k-space and the resultant image field of view (FOV) in image space, we can now better understand the occurrence of aliasing (Fig. 2.17). Decreasing the sample rate in k-space corresponds to a decrease in the spacing of the Dirac comb function in image space (i.e., the FOVx becomes smaller). As a result, the repeated images are no longer separated, but overlap within the reconstructed image window (Fig. 2.17C). These repeated images are commonly termed “ghosts,” or “fold-over” or “wrap-around” artifacts.
Image Bandwidth
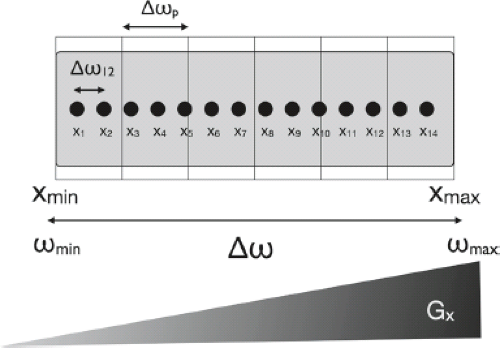
In image space, the FOV and spatial resolution are defined by the pixel and image bandwidth (BW), which are equal to the range of
frequencies contained within a pixel or across the whole object. Along x, the resonant frequency difference, Δω, between two points, xmin and xmax, as a result of the linear field gradient Gx is
frequencies contained within a pixel or across the whole object. Along x, the resonant frequency difference, Δω, between two points, xmin and xmax, as a result of the linear field gradient Gx is
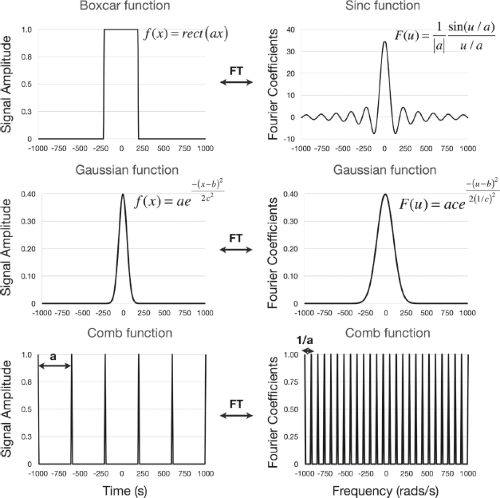 FIGURE 2.15 Common Fourier transform pairs that appear throughout MRI signal acquisition, sampling, and image reconstruction. |
If xmin and xmax define the end points of an object (Fig. 2.18) with corresponding minimum and maximum frequencies ωmax and ωmin, the Δω is related the field of view of the image along x (FOVx) as,
If we can accurately sample the range of frequencies across the FOVx (i.e., our sampling rate meets the Nyquist limit) then the reconstructed image will be free of aliasing.
Spatial resolution can, likewise, be considered within the context of the frequency range contained within each pixel. From the relationship between the image BW and FOVx, the pixel BW across each of the Nx pixels is Δωp = Δω/Nx (Fig. 2.18). Since resolution is a measure of how close two point sources can be and still be distinguished in an image, spatial resolution is directly related to the pixel BW. If the frequency difference between two point sources (Δω12 = γGx(x2−x1)) is less than or equal to the pixel BW (i.e., Δω12/Δωp ≤ 1), the points will be indistinguishable and appear superimposed in the same pixel.
So What Determines the FOV?
There may, at first glance, be confusion regarding the relationship between FOV, image BW, gradient strength, spatial resolution, and sampling rate, since each parameter can be related to the others. We can reconcile this by remembering that the FOV is best characterized as the range of frequencies we can accurately sample (Δω). Thus, for a given field gradient strength, Gx, an increased FOV corresponds to increased range of frequencies across the object. In order to accurately sample the maximum frequency in the object, the sampling rate (ωs) must meet the Nyquist criterion, ωs ≥ 2ωmax. The sampling rate is directly related to the time interval of individual samples (Δt), which is also directly related to Δkx. Therefore, the minimum value of Δt that can be performed by the ADC (termed the receiver BW) directly determines the maximum range of frequencies that can be sampled accurately and, consequently, the maximum FOV.
In our example, if the total number of samples (Nx) and Gx are held constant as the FOV is increased, then the increased pixel BW results in a reduced spatial resolution.
In general, an MR operator need not directly worry about receiver BW, gradient strength, and so forth. Rather, based on the user’s desired FOV and spatial resolution, the scanner computer will determine the appropriate BW and gradient strength. However, an astute operator will aim to minimize the BW for a given scan time, thereby maximizing the sampling interval Δt. This increases the SNR of the resulting image since more signal is acquired per voxel. This is analogous to signal averaging discussed previously, with SNR scaling as
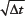 or
or
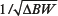 .
.
Sampling in 2D and 3D
2D and 3D imaging are illustrated by the pulse sequence diagrams in Figures 2.3 and 2.6. The phase-encoding steps, Δky and Δkz, are analogous to Δkx, and define the FOV in the y and z dimensions. As a general rule, steps between phase-encoding points are larger than between frequency-encoding points, resulting in aliasing more commonly being associated with phase-encoding directions. Consequently, aliasing is also termed “phase-wrap.”
Motion
For correct image reconstruction, it is imperative that the phase increments (Δky and Δkz) are constant between successive phase-encoding lines. Phase information contributes substantively to the final image, and phase errors between phase-encoding steps can significantly degrade image quality. For example, applying
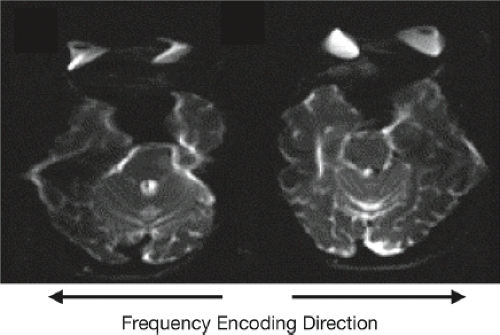
an artifactual 90-degree phase shift to alternating lines in a 2D image introduces a “ghost” into the reconstructed image, shifted by 1/2 FOV (Fig. 2.19B). When random phase errors are added to each phase-encoding line, this create a separate ghost for each line, with each shifted in the phase-encoding direction by a different amount (Fig. 2.19C). This latter case is analogous to patient motion in the phase-encoding direction. As seen in Table 2.1, subject motion in image space corresponds to a phase shift in k-space. It is useful to note that the motion-related ghosts only appear in the direction that the motion occurred (i.e., motion only in the x direction results in ghosting along x, Fig. 2.19D). Motion consisting only of rotation has a different appearance since, by Table 2.1, rotation in image space is also rotation in k-space. Thus, rotation motion will appear as rotating ghosts in the image.
an artifactual 90-degree phase shift to alternating lines in a 2D image introduces a “ghost” into the reconstructed image, shifted by 1/2 FOV (Fig. 2.19B). When random phase errors are added to each phase-encoding line, this create a separate ghost for each line, with each shifted in the phase-encoding direction by a different amount (Fig. 2.19C). This latter case is analogous to patient motion in the phase-encoding direction. As seen in Table 2.1, subject motion in image space corresponds to a phase shift in k-space. It is useful to note that the motion-related ghosts only appear in the direction that the motion occurred (i.e., motion only in the x direction results in ghosting along x, Fig. 2.19D). Motion consisting only of rotation has a different appearance since, by Table 2.1, rotation in image space is also rotation in k-space. Thus, rotation motion will appear as rotating ghosts in the image.
Image Bandwidth, Chemical Shift, and Geometric Distortion
In addition to defining the image FOV and spatial resolution, BW plays an important role in understanding some common image artifacts, including chemical shift and off-resonance image distortion. As illustrated in Figure 2.18, if the gradient-imposed frequency difference between two points of interest is less than pixel BW (i.e., Δω12/Δωp ≤ 1), the two points will appear to overlap in the same pixel. Similarly, we expect that points separated by Δωp will appear one pixel apart. However, differences in spin frequency as a result of chemical composition or variations in the magnetic field can disrupt this carefully arranged relationship between frequency and spatial location.
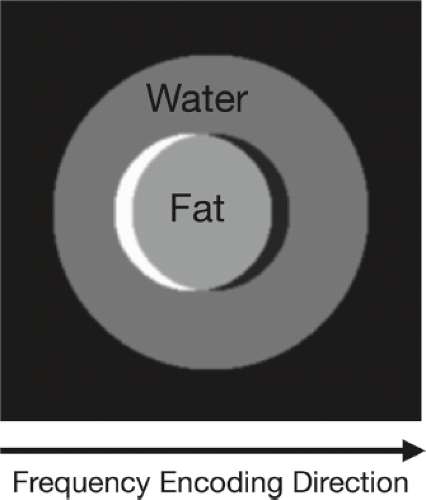
Chemical shift artifacts stem from differences in resonant frequency among spins owing to differences in gyromagnetic ratio or variations in the magnetic field experienced by the nucleus due to surrounding electrons or atoms. A common example in MRI is the hydrogen nuclei associated with fat, which has a chemical shift of ∼147 Hz/T (∼225 Hz at 1.5 T and 450 Hz at 3 T). That is, the hydrogen spins associated with fat have a resonant frequency ∼147 Hz/T less than hydrogen spins associated with water. As a result, if the pixel BW is less than 225 Hz at 1.5 T (or 450 Hz at 3 T), the fat signal will be shifted by at least 1 pixel relative to water signal, even if the fat and water signal originated from the same location (Fig. 2.20). To minimize chemical shift artifacts, the pixel BW must be increased at the expense of SNR.
Shifts in resonant frequency can also result from magnetic susceptibility differences between tissues. When a person is placed in the MRI scanner, not all tissues become magnetized to the same degree. As a result, similar to chemical shift, the resonance frequency of some tissues may be slightly different to other tissues, causing a similar artifact as shown in Figure 2.20 at the tissue boundary. This effect can be most pronounced at tissue–air interfaces, such as near the sinuses or inner ear, where the local magnetic field is significantly altered. This air–tissue susceptibility difference can result in geometric distortions, such as that shown in Figure 2.21.
Filtering
Referring to the Nyquist–Shannon sampling theorem, in order to avoid aliasing, the sampling frequency in k-space must be chosen to be at least twice the highest spatial frequency contained within the object. However, real-world objects comprise effectively infinite spatial frequencies. To deal with this, the incoming signal is first low-pass filtered, the purpose of which is to filter out frequencies larger than the Nyquist limit (i.e., those larger than 1/2Δkx). While this process is normally transparent to the MR technologist or radiologist, an incorrectly set filter may cause a sharp drop in image signal intensity beyond a certain distance from the image center.
Signal Evolution and Relaxation
To this point in our discussion we have allowed the excited net magnetization vector
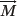 to rotate in the transverse plane without considering its evolution with time. Following excitation by an RF pulse, the net magnetization vector is tipped into the transverse plane where it rotates about the external field at the Larmor frequency, giving rise to the MR signal. A second action of the RF pulse causes the spins to align in orientation, or become phase coherent in the transverse plane. Over time
to rotate in the transverse plane without considering its evolution with time. Following excitation by an RF pulse, the net magnetization vector is tipped into the transverse plane where it rotates about the external field at the Larmor frequency, giving rise to the MR signal. A second action of the RF pulse causes the spins to align in orientation, or become phase coherent in the transverse plane. Over time
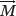 recovers back to equilibrium, with the individual spins returning to their parallel or anti-parallel orientation, and losing their phase coherence. As a result,
recovers back to equilibrium, with the individual spins returning to their parallel or anti-parallel orientation, and losing their phase coherence. As a result,
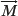 reforms along the z-axis, parallel with the applied main magnetic field
reforms along the z-axis, parallel with the applied main magnetic field
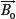 , and with a magnitude of M0. This return to equilibrium is characterized by two orthogonal processes: longitudinal (T1) and transverse (T2) relaxation, governed by the T1 and T2 relaxation time constants. T1 relaxation describes the recovery of
, and with a magnitude of M0. This return to equilibrium is characterized by two orthogonal processes: longitudinal (T1) and transverse (T2) relaxation, governed by the T1 and T2 relaxation time constants. T1 relaxation describes the recovery of
 along the longitudinal (z) direction (with the T1 time corresponding to the recovery of 63% of the equilibrium value), whilst T2 characterizes the loss of phase coherence in the transverse plane (with the T2 time corresponding to the loss of 63% of the initial value). Each of these processes can be described by exponential functions, with the longitudinal component of
along the longitudinal (z) direction (with the T1 time corresponding to the recovery of 63% of the equilibrium value), whilst T2 characterizes the loss of phase coherence in the transverse plane (with the T2 time corresponding to the loss of 63% of the initial value). Each of these processes can be described by exponential functions, with the longitudinal component of
 returning to its equilibrium value, M0, by
returning to its equilibrium value, M0, by
and the transverse component of
 decaying from its initial value (Mxy,0) to 0 as
decaying from its initial value (Mxy,0) to 0 as
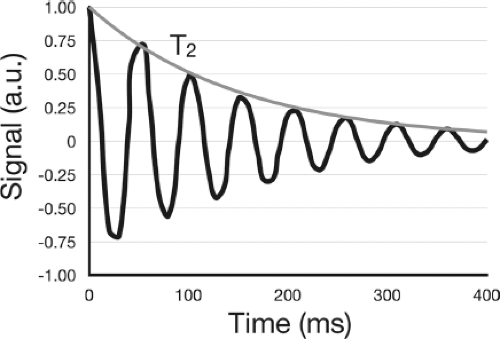
Each of these functions are illustrated in Figure 2.22.
Decay of the transverse magnetization by T2 processes assumes a perfectly homogeneous magnetic field. In practice, this is impossible to achieve and, as a result, the transverse magnetization decays according to a modified T2 relaxation constant, T*2,
where
T2′ reflects the dephasing due to macroscopic magnetic field inhomogeneities. In general, T*2 < T2 ≪ T1.
The MRI signal following an RF pulse, therefore, is an oscillating signal with an envelope defined ideally by Eqn. [12], but more practically given magnetic field inhomogeneities by Eqn. [13], as shown in Figure 2.23. This is termed a free induction decay (FID).
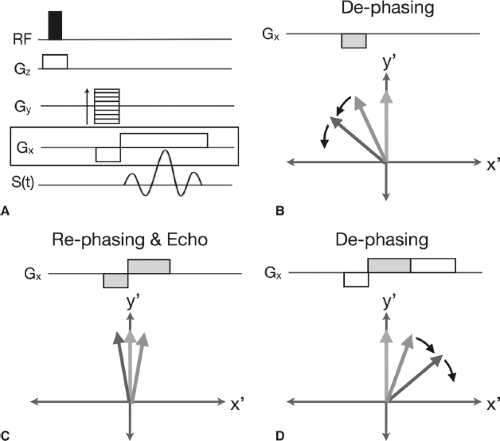
In practice, the FID decays too quickly to measure directly. Instead, we measure an echo of the FID, produced using either a gradient (gradient echo) or an additional 180-degree RF pulse (spin echo). To examine how these echoes are produced, we first consider the gradient echo and return our attention to the readout gradient in a simple pulse sequence (Fig. 2.24A).
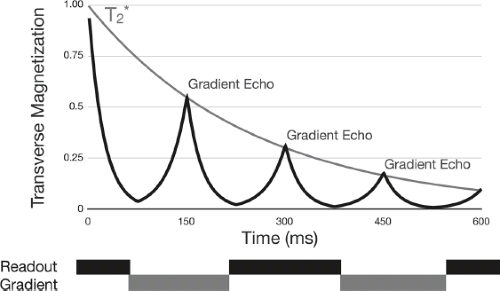
From our discussion on sampling, we recognize that the duration and amplitude of the Gx gradient describe a trajectory in k-space along kx (the negative lobe moves our position to −kx), and the subsequent positive lobe moves our position along the line to +kx passing through kx = 0. Although it may not be clear in Figure 2.24A, it is important to note that the area of the negative lobe is exactly half the area of the positive lobe. We now ask, what is the action of this gradient on the orientation of spins in our sample? This is more directly examined in the rotating frame of reference (Fig. 2.24B–D). The initial negative lobe causes dephasing of the magnetization vectors across the sample (in addition to the inherent dephasing caused by T*2). The first half of the positive lobe reverses the gradient-induced dephasing, causing the magnetization vectors to rephase. Because of T*2 dephasing during the negative and positive lobes, the vectors do not perfectly align but, nevertheless, create a signal echo. Finally, the second half of the positive lobe causes the magnetization vectors to dephase again. In gradient-echo EPI, a “train” of gradient echoes are created by continuously reversing polarity (sign) of Gx (Fig. 2.25).
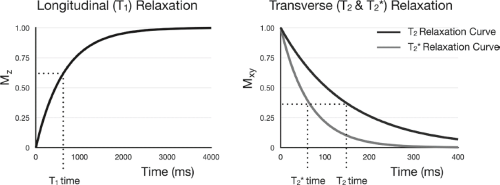 FIGURE 2.22 Recovery of the longitudinal magnetization via T1 relaxation, and decay of the transverse relaxation via T2 and T*2 relaxation. |
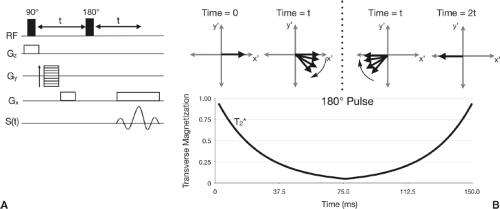
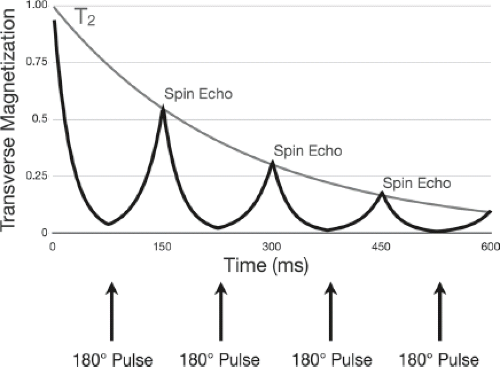
To eliminate the effects of local macroscopic magnetic field inhomogeneities on the magnetization decay (i.e., have the decay described by T2 and not T*2), a spin echo pulse sequence can be used (Fig. 2.26A). This sequence differs from our prior examples in that it contains a second RF pulse, which rotates the magnetization 180 degrees. Examining the magnetization in the rotating frame offers insight into how this sequence forms a measurable echo (Fig. 2.26B). Following the initial RF pulse, the transverse magnetization begins to dephase according to
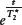 . The 180-degree pulse acts to invert the spin system, causing the spins to rephase and form an echo at time 2 t.
. The 180-degree pulse acts to invert the spin system, causing the spins to rephase and form an echo at time 2 t.
A common analogy for the spin echo is a foot race. After starting in line, the runners spread out as some run faster than others. At time t, a gun is fired and the runners turn around and run back to the starting line. The faster runners catch back up to the slower ones, and they all arrive back at the starting line at time 2 t. In this analogy, the faster runners are those experiencing greater field inhomogeneities. A train of spin echoes can be created by applying a succession of 180-degree inversion pulses (Fig. 2.27). This approach is the basis of fast spin echo (FSE) and spin echo EPI pulse sequences (2,3,4).
Part II: Mechanisms and Manipulation of Image Contrast
An essential requirement of any radiologic image is that it contain sufficient contrast with which to discriminate between different tissues (e.g., white and gray matter in the central nervous system), and between healthy tissue and pathology (e.g., tumorous vs. healthy tissue, or between healthy tissue, ischemic penumbra, and ischemic core following stroke). Image contrast is conventionally defined as the mean signal difference between two tissues or regions of interest,
However, as MR images also contain noise, which can obscure subtle differences in mean signal, a more useful measure is often the contrast-to-noise ratio (CNR),
where σ0 is the standard deviation of the background noise. Arguably, CNR is a more useful measure of image quality in a radiologic context than SNR, since even an image with no noise but devoid of contrast may have little diagnostic utility. In addition to raw image CNR, we can also account for our visual system’s ability to average over large areas of an image, improving the effective CNR of the image by the square root of the number of pixels comprising each tissue. This can be combined into a measure of visibility that reflects the likelihood of detecting an object against a background (such as a lesion within tissue) as
In a diagnostic setting, the Rose criterion states that for images to have sufficient useable contrast and be easily interpretable, ν should be at least 4.
MRI is unique amongst radiologic imaging techniques in that image contrast may be manipulated to an almost infinite degree by varying the acquisition strategy and parameters. This contrasts with x-ray, computed tomography (CT), and ultrasound (US) imaging, in which contrast is essentially fixed and depends on tissue density. Over the course of this section, we will examine the fundamental biologic mechanisms of contrast, and explore current approaches to exploiting and maximizing this inherent contrast.
Biophysical Basis of Relaxation and Proton Density
The acquisition and interpretation of T1, T2, or PD-weighted images is familiar to most clinicians. Indeed, the exquisite soft tissue contrast provided by MRI arises principally due to the differences in these intrinsic relaxation properties. We have seen previously that T1 and T2 processes describe the recovery of the longitudinal and transverse magnetizations to their equilibrium values. PD refers to the number of proton spins per unit volume, and is related principally to the amount of free water within the investigated tissue.
Intrinsically, T1 and T2 relaxations are processes of molecular motion, molecular interaction, and energy exchange. These phenomena arise due to fluctuations in the local magnetic field experienced by each proton spin. In particular, T1 relaxation involves an exchange of energy between water protons and protons attached to other surrounding lipids, proteins, and macromolecules (collectively termed the “lattice”). To acknowledge these interactions, T1 relaxation is also commonly referred to as spin–lattice relaxation. In contrast, T2 relaxation results from interactions between the water protons themselves and, accordingly, is also termed spin–spin relaxation. An important distinction between T1 and T2 processes is that while T1 is an energy-loss process (with energy transferred from the water
protons to the bulk lattice), T2 is an energy-conserving process, resulting solely from the dephasing of the individual spin magnetic moments in an ensemble.
protons to the bulk lattice), T2 is an energy-conserving process, resulting solely from the dephasing of the individual spin magnetic moments in an ensemble.
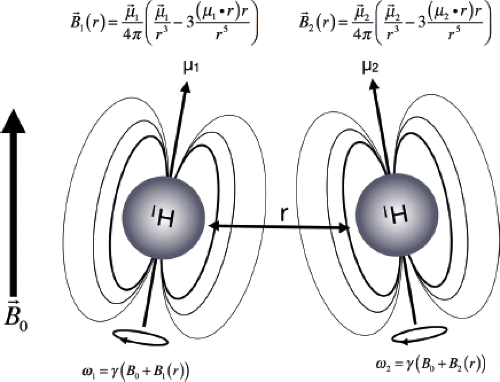
As individual spins freely move and diffuse throughout a spin system, they produce and experience a rapidly varying magnetic field environment. From Figure 2.28, the small magnet moment associated with each spin acts as a small magnetic field perturber, altering the magnetic field experience by local protons (Fig. 2.29). Since the precessional frequency of a proton is governed by the magnitude of the local magnetic field, these small variations will differentially alter the precessional frequencies across an ensemble of spins. The effect of this variation is perhaps easiest to understand in the context of T2 decay. In a collection of spins with their magnetic moments initially aligned, or in-phase, each spin will experience slightly different field variations as they diffuse and collide. Over time these field and associated precessional frequency differences lead to a loss in the phase coherence across the spin ensemble, and a reduction of the net magnetic moment in the transverse plane.
T1 is similarly driven by magnetic field fluctuations. If we consider two proton spins vibrating next to each other, each creates a sinusoidally varying magnetic field that is experienced by the other spin, and is analogous to the varying magnetic field resulting from an RF pulse. If the frequency of vibration is equal to the Larmor frequency, it can induce a rotation in the spin’s magnetic moment. Of course, molecular motion is far more complex than simple vibration, but this example provides the underlying mechanism of T1 relaxation. As protons move, collide, rotate, and interact with other water and lattice protons, they experience a time-varying magnetic field. If a component of that variation is at the Larmor frequency, it will induce a rotation of the spin similar to an RF pulse. This result suggests that T1 relaxation will have a strong field dependence due to its relationship to the Larmor frequency.
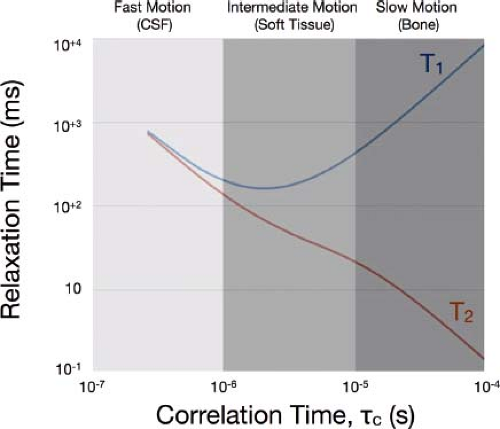
The first theoretical relationship to link relaxation to magnetic proton–proton interactions and molecular motion was presented by Bloembergen, Purcell, and Pound (BPP) (5) in their seminal 1948 paper. Although derived for protons in homogeneous aqueous solutions, the BPP theory of relaxation provides expressions for T1 and T2 that are extremely useful, and offer general insight into the relationships between relaxation and tissue structure. They are summarized here as
and
Equations [47] and [48] relate relaxation time, Larmor frequency (ω), molecular rotational motion (denoted by τC, or the correlation time), and the strength of proton interactions (K). The correlation time can be interpreted as a measure of molecular motion and reorientation (or tumbling). Short correlation times describe rapid motion, and long correlation times correspond to slow molecular motions. Graphical evaluations of these expressions (Fig. 2.30) demonstrate the behavior of T1 and T2 over a range of correlation times, and can be used to infer their values in different biophysical environments. Regions of fast molecular motion are most associated with aqueous environments, such as the cerebral spinal fluid (CSF), blood, or areas of inflammation or edema. Soft tissues, such as
brain gray and white matter, fat, muscle, and tendon would correspond to intermediate motion. Finally, long correlation times are associated with rigid structures, such as bone.
brain gray and white matter, fat, muscle, and tendon would correspond to intermediate motion. Finally, long correlation times are associated with rigid structures, such as bone.
Though both T1 and T2 are sensitive to motion at the Larmor frequency, the additional τc term in the T2 expression accurately describes the sensitivity of T2 to slow molecular motions, such as in rigid structures, including bone and teeth, which are difficult to image due to their rapid signal decay. In unrestricted aqueous environments, such as CSF, T2 is approximately equal to T1. Representative T1 and T2 values for gray matter, white matter, spinal cord, and optic nerve at 1.5, 3, and 7 T are presented in Table 2.2 (a more extensive review of relaxation times in various tissues and across field strengths is provided by Bottonley et al. (6)). The enhanced sensitivity of T1 to motion at the Larmor frequency explains the prolongation of T1 for tissues other than CSF at higher field strengths, T1 varying with field strength as
where Y is a proportionality constant and the exponent k varies from 0.3 to 0.5 depending on tissue.
In addition to the magnetic field fluctuations caused by molecular motions, variations in the local magnetic field are also caused by macroscopic inhomogeneities in the external magnetic field and the presence of large paramagnetic molecules with different magnetic susceptibilities from tissue. These larger scale variations accelerate the signal decay and can be characterized by an additional T2 term, denoted T2′. The signal decay caused by the combination of molecular motion and macroscopic inhomogeneity is denoted by T*2 and was given in the previous section by Eqn. [14].
As both T1 and T2 (and T*2) result from molecular motion, they are directly influenced by the local tissue structure and biochemical environment. Micro- and macrostructural characteristics including tissue density (water content and mobility), macromolecule, protein, and lipid composition, and paramagnetic atom (e.g., iron) concentration all influence T1 and T2. Thus, changes in relaxation times can be indicative of disease or pathology, or reflective of other important biologic processes, including neurodevelopment, neuroplasticity, and neurodegeneration. Though it seems obvious now that the microstructural differences between tissues would lead to measurable T1 and/or T2 differences, it was not until 1971, some 33 years after the discovery of the NMR phenomenon in solids (7) and the first detailed theory of NMR relaxation (5), that T1 and T2 were shown to vary across tissues (8), and later still that they were shown to change with pathology (9).
To exploit relaxation time differences in a conventional T1 or T2 weighted image, the image contrast is made sensitive to tissue differences through the choice of imaging pulse sequence and the manipulation of acquisition parameters. For example, the tissue contrast within a spoiled gradient recalled echo (SPGR) image can be made more or less sensitive to T1 differences by varying the repetition time (TR), echo time (TE), flip angle (α), or adding magnetization preparation pulses.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree