(3.1)
The radiation used in radiation therapy includes high-energy X-rays and gamma rays, which are types of electromagnetic waves. Their energy in radiation therapy is expressed in the unit of MeV. The energy of an electromagnetic wave E is expressed by the following equation including Planck’s constant h:
![$$ E\left[\mathrm{M}\mathrm{e}\mathrm{V}\right]=h\cdot \nu =\frac{h\cdot c}{\lambda}\approx 4.14\times {10}^{-21}\cdot \nu \left[{\mathrm{s}}^{\hbox{-} 1}\right]\approx 1.24\times {10}^{-12}/\lambda \left[\mathrm{m}\right]. $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_Equ2.gif)
(3.2)
As shown in Fig. 3.1, when matter is irradiated with an incident charged particle, an electromagnetic wave is released from outside of the nucleus in the form of an X-ray, while one is released by the nucleus in the form of a gamma ray. When the incident charged particle is an electron, bremsstrahlung is produced when the direction of the electron is deflected by the Coulomb force of the nucleus of the matter during its passage through the matter.
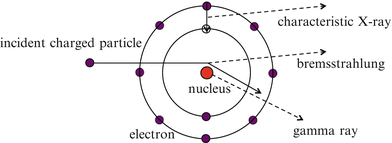

Fig. 3.1
The release of X-rays and gamma rays
Characteristic X-rays are electromagnetic radiation with a certain energy whose release corresponds to the filling of an outer-shell electron vacancy produced by the emission of an inner-shell electron of an atom of matter.
3.2 Interactions of Photons with Matter
Interactions of photons with matter depend on the energy of the photons. These interactions include the photoelectric effect, Rayleigh scattering (coherent scattering), Compton scattering (incoherent scattering), pair production, and photonuclear reaction. In radiation therapy, transfer of the energy possessed by photons to matter (i.e. a tumor) is important; it is necessary for this energy to be transferred from photons to electrons, which are charged particles. Therefore, the photoelectric effect, Compton scattering, and pair production are important interactions of photons with matter in radiation therapy (see Fig. 3.2).
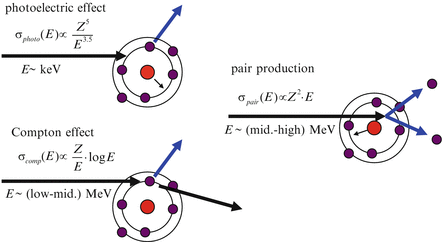

Fig. 3.2
The interactions of incident photons with matter
3.2.1 Photoelectric Effect
The photoelectric effect is a reaction involving the loss of energy that is caused when photons of relatively low energy are absorbed by matter and bound electrons of atoms or molecules in that matter are released. The maximum kinetic energy E e that is carried by an electron is given by the following equation. The term W is the work function, which means the minimum energy required to remove an electron from the binding of an atom or a molecule in the matter.
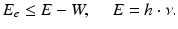
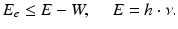
(3.3)
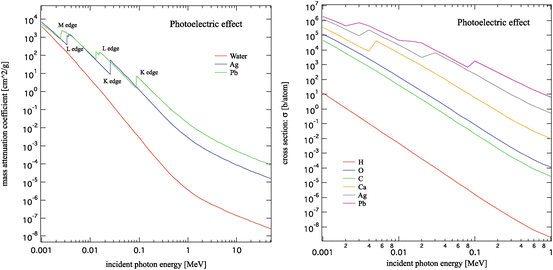
The energy of a photon absorbed by the matter produces excitation of an atom; this excited atom then returns to its stable ground state by ejecting an Auger electron and an X-ray. Figure 3.3 shows the results of the mass attenuation coefficients 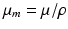 for water, silver, and lead and the cross section as a function of the energy of the incident photon in the photoelectric effect [1]. The term ρ is the density and μ is the attenuation coefficient. The photoelectric effect tends to emit inner-shell electrons (K-shell, L-shell, and M-shell), which are bound at a higher level of energy; in this regard, the effect causes a physical phenomenon in which an atom made unstable by absorption of the energy of a photon releases a high level of energy each time, but with a smaller number of reactions. As a result, the plot for the cross section of the photoelectric effect shows changes in a stepwise manner according to the bound energies of electrons (see Fig. 3.3).
for water, silver, and lead and the cross section as a function of the energy of the incident photon in the photoelectric effect [1]. The term ρ is the density and μ is the attenuation coefficient. The photoelectric effect tends to emit inner-shell electrons (K-shell, L-shell, and M-shell), which are bound at a higher level of energy; in this regard, the effect causes a physical phenomenon in which an atom made unstable by absorption of the energy of a photon releases a high level of energy each time, but with a smaller number of reactions. As a result, the plot for the cross section of the photoelectric effect shows changes in a stepwise manner according to the bound energies of electrons (see Fig. 3.3).
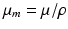 for water, silver, and lead and the cross section as a function of the energy of the incident photon in the photoelectric effect [1]. The term ρ is the density and μ is the attenuation coefficient. The photoelectric effect tends to emit inner-shell electrons (K-shell, L-shell, and M-shell), which are bound at a higher level of energy; in this regard, the effect causes a physical phenomenon in which an atom made unstable by absorption of the energy of a photon releases a high level of energy each time, but with a smaller number of reactions. As a result, the plot for the cross section of the photoelectric effect shows changes in a stepwise manner according to the bound energies of electrons (see Fig. 3.3).
for water, silver, and lead and the cross section as a function of the energy of the incident photon in the photoelectric effect [1]. The term ρ is the density and μ is the attenuation coefficient. The photoelectric effect tends to emit inner-shell electrons (K-shell, L-shell, and M-shell), which are bound at a higher level of energy; in this regard, the effect causes a physical phenomenon in which an atom made unstable by absorption of the energy of a photon releases a high level of energy each time, but with a smaller number of reactions. As a result, the plot for the cross section of the photoelectric effect shows changes in a stepwise manner according to the bound energies of electrons (see Fig. 3.3).
Fig. 3.3
The mass attenuation coefficient and the cross section as functions of the energy of the incident photon in the photoelectric effect [1]
The cross section of the photoelectric effect is approximately inversely proportional to the 3.5th power of energy of the incident photon and proportional to the 5th power of the atomic number of the matter. In addition, it is proportional to the 3.5th power of the effective atomic number of the matter.
3.2.2 Compton Scattering
Compton scattering is a scattering phenomenon between a photon and an electron that is caused when the energy of the incident photon is much higher than the bound energy of the electron. The electron is given some of the energy of the incident photon and travels with that given energy as its kinetic energy, while the scattered photon loses energy. When the energy of the incident photon is far lower than the mass energy of the electron, the incident photon hardly loses energy by scattering with an electron. This phenomenon is called Thomson scattering. It is not necessary to consider this scattering phenomenon for photons with energy on the order of MeV, as used in radiation therapy.
As represented in Fig. 3.4, the following equation is given by the law of conservation of momentum and energy in Compton scattering:
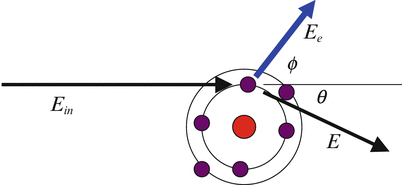
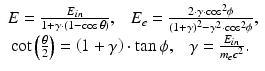
where E in is the energy of the incident photon, E is the energy of the scattered photon, θ is the scattering angle of the scattered photon, E e is the energy of the recoil electron, and ϕ is the scattering angle of the recoil electron. The quantity of ![$$ {m}_e\cdot {c}^2\approx 0.511\left[\mathrm{M}\mathrm{e}\mathrm{V}\right] $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_IEq2.gif) is the rest mass energy of an electron. A recoil electron receives the maximum energy by Compton scattering when the scattering angle of the recoil electron
is the rest mass energy of an electron. A recoil electron receives the maximum energy by Compton scattering when the scattering angle of the recoil electron  ; and the following equation can then be derived from Eq. (3.4):
; and the following equation can then be derived from Eq. (3.4):
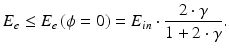
The edge of the energy spectrum of a recoil electron with the maximum recoil energy is called the Compton edge. The difference between the wavelength of an incident photon and that of a scattered photon depends on the scattering angle θ, not on the energy of the incident photon or the scattered photon.

Fig. 3.4
The Compton effect
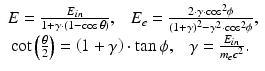
(3.4)
![$$ {m}_e\cdot {c}^2\approx 0.511\left[\mathrm{M}\mathrm{e}\mathrm{V}\right] $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_IEq2.gif) is the rest mass energy of an electron. A recoil electron receives the maximum energy by Compton scattering when the scattering angle of the recoil electron
is the rest mass energy of an electron. A recoil electron receives the maximum energy by Compton scattering when the scattering angle of the recoil electron 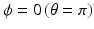 ; and the following equation can then be derived from Eq. (3.4):
; and the following equation can then be derived from Eq. (3.4):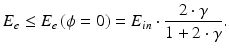
(3.5)
The differential cross section of Compton scattering per unit of solid angle is given by the Klein-Nishina formula:
![$$ \frac{d{\sigma}_{comp}\left({E}_{in}\right)}{d\Omega}={r_e}^2\cdot \frac{\left(1+{ \cos}^2\theta \right)}{2{\left\{1+\gamma \cdot \left(1- \cos \theta \right)\right\}}^2}\times \left[1+{\gamma}^2\cdot \frac{{\left(1- \cos \theta \right)}^2}{{\left(1+ \cos \theta \right)}^2\cdot \left\{1+\gamma \cdot \left(1- \cos \theta \right)\right\}}\right]. $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_Equ6.gif)
![$$ {r}_e=\frac{e^2}{m_e\cdot {c}^2}\approx 2.818\times {10}^{-13}\left[ cm\right]. $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_Equ7.gif)
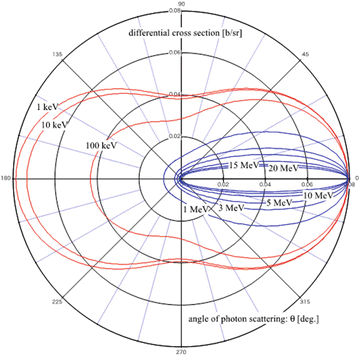
The term r e is the classical electron radius. Figure 3.5 shows the results of calculation for the differential cross section of Compton scattering for every angle of a scattered photon as a function of the energy of the incident photon using Eqs. (3.6) and (3.7). The red lines in the figure represent the cases of incident photons with energy in the range of 1–100 keV, while the blue lines show those in the range of 1–10 MeV. As shown in the figure, the possibility of causing forward scattering increases when the energy of the incident photon becomes higher. This possibility is extremely high and Compton scattering tends to deposit energy of the incident photon forward for energy on the order of MeV (blue line in the figure), as used in radiation therapy.
![$$ \frac{d{\sigma}_{comp}\left({E}_{in}\right)}{d\Omega}={r_e}^2\cdot \frac{\left(1+{ \cos}^2\theta \right)}{2{\left\{1+\gamma \cdot \left(1- \cos \theta \right)\right\}}^2}\times \left[1+{\gamma}^2\cdot \frac{{\left(1- \cos \theta \right)}^2}{{\left(1+ \cos \theta \right)}^2\cdot \left\{1+\gamma \cdot \left(1- \cos \theta \right)\right\}}\right]. $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_Equ6.gif)
(3.6)
![$$ {r}_e=\frac{e^2}{m_e\cdot {c}^2}\approx 2.818\times {10}^{-13}\left[ cm\right]. $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_Equ7.gif)
(3.7)

Fig. 3.5
The differential cross section of Compton scattering for every angle of a scattered photon as a function of the energy of the incident photon
The total cross section of Compton scattering σ comp is given by integrating the differential cross section of Compton scattering (Eq. (3.6)) with the total solid angle. The result of the integral calculation is shown in Eq. (3.8).
![$$ \begin{array}{l}{\sigma}_{comp}\left({E}_{in}\right)={\displaystyle \underset{0}{\overset{4\cdot \pi }{\int }}\left(d{\sigma}_{comp}\left({E}_{in}\right)/d\Omega \right)d\Omega}\\ {}=2\cdot \pi \cdot {r_e}^2\cdot [\frac{1+\gamma }{\gamma^2}\cdot \left\{\frac{2\cdot \left(1+\gamma \right)}{1+2\cdot \gamma }-\frac{1}{\gamma}\cdot \ln \left(1+2\cdot \gamma \right)\right\}+\frac{1}{2\cdot \gamma}\cdot \ln \left(1+2\cdot \gamma \right)-\frac{1+3\cdot \gamma }{{\left(1+2\cdot \gamma \right)}^2}].\end{array} $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_Equ8.gif)
When the total cross section of Compton scattering is divided into the cross section of the Compton scattered photon σ s and the cross section of the recoil electron σ a , the following equation is given:
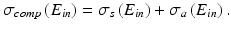
![$$ \begin{array}{l}{\sigma}_{comp}\left({E}_{in}\right)={\displaystyle \underset{0}{\overset{4\cdot \pi }{\int }}\left(d{\sigma}_{comp}\left({E}_{in}\right)/d\Omega \right)d\Omega}\\ {}=2\cdot \pi \cdot {r_e}^2\cdot [\frac{1+\gamma }{\gamma^2}\cdot \left\{\frac{2\cdot \left(1+\gamma \right)}{1+2\cdot \gamma }-\frac{1}{\gamma}\cdot \ln \left(1+2\cdot \gamma \right)\right\}+\frac{1}{2\cdot \gamma}\cdot \ln \left(1+2\cdot \gamma \right)-\frac{1+3\cdot \gamma }{{\left(1+2\cdot \gamma \right)}^2}].\end{array} $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_Equ8.gif)
(3.8)
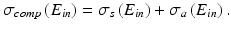
(3.9)

![$$ \begin{array}{l}{\sigma}_s\left({E}_{in}\right)={\displaystyle \underset{0}{\overset{4\cdot \pi }{\int }}\left[{\left\{1+\gamma \cdot \left(1- \cos \theta \right)\right\}}^{-1}\cdot \left(d{\sigma}_{comp}\left({E}_{in}\right)/d\Omega \right)\right]d\Omega}\\ {}=\pi \cdot {r_e}^2\cdot \left[\frac{1}{\gamma^3}\cdot \ln \left(1+2\cdot \gamma \right)+\frac{2\cdot \left(1+\gamma \right)\cdot \left(2\cdot {\gamma}^2-2\cdot \gamma -1\right)}{\gamma^2\cdot {\left(1+2\cdot \gamma \right)}^2}+\frac{8\cdot {\gamma}^2}{3\cdot {\left(1+2\cdot \gamma \right)}^3}\right].\end{array} $$](/wp-content/uploads/2016/11/A322115_1_En_3_Chapter_Equ10.gif)