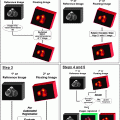
Fig.4.1
Examples of the planetary model of the atom are shown for (a) hydrogen (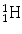
) and (b) fluorine-18 (
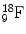). Protons are indicated by the solid circles, neutrons by the hollow circles and circulating electrons by the gray circles
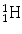) and (b) fluorine-18 (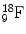). Protons are indicated by the solid circles, neutrons by the hollow circles and circulating electrons by the gray circles We shall continue to use this basic model of the atom for much of our discussion. The model breaks down in the realm of quantum mechanics, where Newtonian physics and the laws of motion no longer apply and as particles approach relativistic speeds (i.e., approaching the speed of light). Also, there are times when we must invoke a non-particulate model of the atom where the particles need to be viewed as waves (or, more correctly, wave functions). Electrons, for example, can be considered at times to be waves. This helps to explain how an electron can pass through a “forbidden” zone between energy levels and appear in the next level without apparently having passed through the forbidden area, defined as a region of space where there is zero probability of the existence of an electron. It can do so if its wave function is zero in this region. For a periodic wave with positive and negative components, this occurs when the wave function takes a value of zero. Likewise, electromagnetic radiation can be viewed as particulate at times and as a wave function at other times. The planetary model of the atom is composed of nucleons (protons and neutrons in the nucleus of the atom) and circulating electrons. It is now known that these particles are not the fundamental building blocks of matter but are themselves composed of smaller particles called quarks.
Energy and Mass
Energy and Frequency
In 1900, Max Planck made the important observation that the energy (E) of electromagnetic radiation was simply related to the frequency of the radiation (υ) by a single constant (Planck’s constant, h):
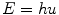
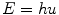
Planck’s constant has a value of 6.626 × 10−34 J s. This provided support to the notion that electromagnetic radiation behaved like a wave. In addition, experiments indicated that the radiation was only released in discrete “bursts.” This was a startling result as it departed from the classical assumption of continuous energy to one in which electromagnetic radiation could only exist in integral multiples of the product of hυ. The wave-like radiation was said to be quantized, where each quantum contained an amount of energy that was an integer multiple of hυ. The unit of energy in the SI system is the Joule (J); however, a derived unit used frequently in discussions of the energy of electromagnetic and particulate radiation is the electron volt (eV). The electron volt is defined as the energy acquired when a unit charge is moved through a potential difference of one volt. Energy in Joules can be converted to energy in electron volts (eV) by dividing by the conversion factor 1.6 × 10−19 J eV−1. Thus, the energy in Joules for visible light photons of, for example, 450 nm would be
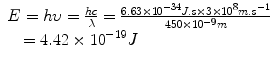which can be expressed in units of eV as
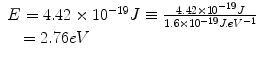
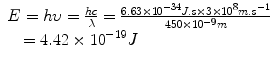
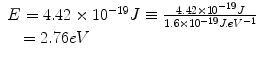
X-rays and gamma rays have energies of thousands to millions of electron volts per photon (keV–MeV).
Energy and Mass Equation
Einstein’s special theory of relativity published in 1905 predicted, among other things, that the speed of light was constant for all observers independent of their frame of reference (and therefore, that time was no longer constant), and, importantly, that mass and energy were equivalent. This means that we can talk about the rest-mass equivalent energy of a particle, which is the energy that would be liberated if all of the mass were to be converted to energy. By rest mass, we mean that the particle is considered to be at rest, that is, it has no kinetic energy. Consider the electron, which has a rest mass of 9.11 × 10−31 kg; we can calculate the amount of energy this mass is equivalent to using Einstein’s equation:
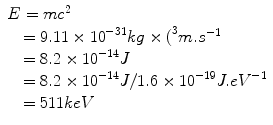
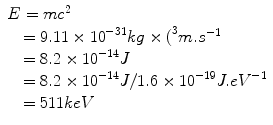
The reader may recognize this as the energy of the photons emitted in positron–electron annihilation (Fig. 4.2).
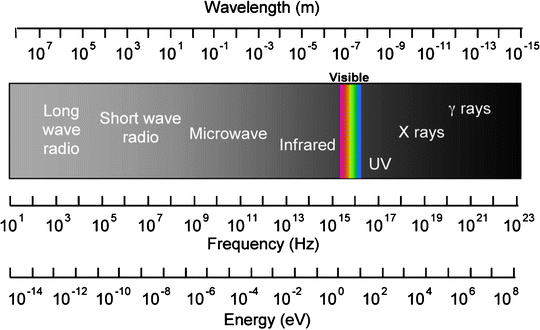
Fig. 4.2
The electromagnetic spectrum showing energy in units of eV
Radioactivity and Radiation
Radiation can be classified into electromagnetic or particulate. Ionizing radiation is radiation that has sufficient energy associated with it to remove electrons from atoms, thus causing ionization. This is restricted to high-energy electromagnetic radiation (X and γ radiation) and charged particles (α++, β−, β+). Examples of non-ionizing electromagnetic radiation include light, radio, and microwaves. We will concern ourselves specifically with ionizing radiation as this is of most interest in nuclear medicine and radiological imaging.
Electromagnetic Radiation
Electromagnetic radiation is pure energy. The amount of energy associated with each “bundle,” or quantum, of energy is determined by the frequency or wavelength (λ) of the radiation. Human senses are capable of detecting some forms of electromagnetic radiation, for example, thermal radiation, or heat, (λ ≈ 10−5 m), and visible light (λ ≈ 10−7 m). The energy of the radiation can be absorbed to differing degrees by different materials: light can be stopped (absorbed) by paper, whereas radiation with longer wavelength (e.g., radio waves) or higher energy (γ-rays) can penetrate the same paper.
It had long been known that light acted like a wave, most notably because it caused interference patterns from which the wavelength of the light could be determined. Radiation was thought to emanate from its point of origin like ripples on the surface of a pond after a stone is dropped into it. This concept was not without its difficulties, most notably, the nature of the medium through which the energy was transmitted. This proposed medium was known as the “ether,” and many experiments sought to produce evidence of its existence to no avail. Einstein, however, interpreted some experiments performed at the turn of the twentieth century where light shone on a photocathode could induce an electric current (known as the photoelectric effect) as showing that light acted as a particle. Einstein proposed that radiant energy was quantized into discrete packets, called photons. Thus, electromagnetic radiation could be viewed as having wave-like and particle-like properties. This view persists to this day and is known as the wave-particle duality. In 1924, Louis Victor, the Duc de Broglie, proposed that if wave-particle duality could apply to electromagnetic radiation, it could also apply to matter. It is now known that this is true: electrons, for example, can exhibit particle-like properties such as when they interact like small billiard balls or wave-like properties as when they undergo diffraction. Electrons can pass from one position in space to another, separated by a “forbidden zone” in which they cannot exist, and one way to interpret this is that the electron as a wave that has zero amplitude within the forbidden zone. The electrons could not pass through these forbidden zones if viewed strictly as particles. An important subsequent postulate proposed by Neils Bohr was that de Broglie’s principle of wave-particle duality was complementary. He stated that either the wave or the particle view can be taken to explain physical phenomena, but not both at the same time.
Electromagnetic radiation has different properties depending on the wavelength, or energy, of the quanta. Only higher energy radiation has the ability to ionize atoms, due to the energy required to remove electrons from atoms. Electromagnetic radiation which can cause ionization is restricted to X- and γ-rays, which are discussed in the following sections.
X-Rays
X-rays are electromagnetic radiation produced within an atom but outside of the nucleus. Characteristic X-rays are produced when orbital electrons drop down to fill vacancies in the atom after an inner shell electron is displaced, usually by firing electrons at a target in a discharge tube. As the outer shell electron drops down to the vacancy, it gives off energy, and this is known as a characteristic X-ray as the energy of the X-ray is determined by the difference in the binding energies between the electron levels (Fig. 4.3).
Fig. 4.3
The production of characteristic X-rays is shown. The electron (A) causes a vacancy at B with the liberated electron (C) leaving the atom. An outer shell electron (D) drops down to fill the vacancy and, in doing so, gives off a discrete amount of radiation as a characteristic X-ray
As any orbital electron can fill the vacancy, the quanta emitted in this process can take a number of energies. The spectrum is characteristic, however, for the target metal, and this forms the basis of quantitative X-ray spectroscopy for sample analysis. The spectrum of energies emerging in X-ray emission displays a continuous nature, however, and this is due to a second process for X-ray production known as Bremsstrahlung (German: “braking radiation”).
Bremsstrahlung radiation is produced after a free electron with kinetic energy is decelerated by the influence of a heavy target nucleus. The electron and the nucleus interact via a Coulomb (electrostatic charge) interaction, the nucleus being positively charged and the electron carrying a single negative charge. The process is illustrated in Fig. 4.4. The electron loses kinetic energy after its deceleration under the influence of the target nucleus, which is given off as electromagnetic radiation. There will be a continuum of quantized energies possible in this process depending on the energy of the electron, the size of the nucleus, and other physical factors, and this gives the continuous component of the X-ray spectrum. X-rays generally have energies in the range of ∼103–105 eV and can be used for imaging as well as therapy (Fig. 4.5).
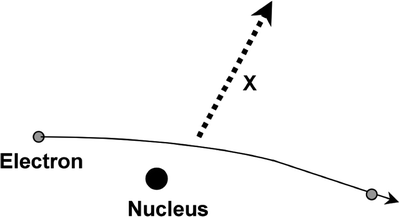
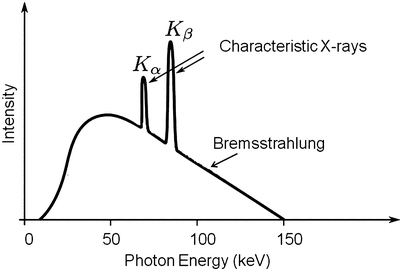
Fig. 4.4
Continuous radiation emitted by an electron under the influence of the nucleus is known as Bremsstrahlung
Fig. 4.5
An example of an X-ray spectrum is shown demonstrating both the Brehmsstrahlung and characteristic components
Gamma Radiation (γ)
Gamma rays are electromagnetic radiation emitted from the nucleus after a spontaneous nuclear decay. This is usually associated with the emission of an alpha or beta particle, although there are alternative decay schemes. X- and γ-rays are indistinguishable after they are emitted from the atom and only differ in their site of origin. After the emission of a particle in a radioactive decay, the nucleus can be left in an excited state, and this excess energy is given off as a γ-ray. Gamma ray emission is characteristic, and it is determined by the difference in energy levels between the initial and final state of the energy level transitions within the nucleus.
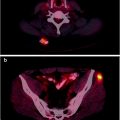
Annihilation Radiation
Annihilation radiation (γ±) is the energy produced in the form of photons (usually two) by the positron–electron annihilation process (Fig. 4.6). The energy of the radiation is equivalent to the rest mass of the electron and positron. Annihilation radiation, arising from positron–electron annihilation, is produced outside of the nucleus and often outside of the positron-emitting atom. There are two photons produced by each positron decay and annihilation. Each photon has energy of 0.511 MeV, and the photons are given off at close to 180° opposed directions. It is this property of colinearity that we exploit in positron emission tomography (PET), allowing us to define the line-of-sight of the event without the need for physical collimation. The general equation for β + decay is
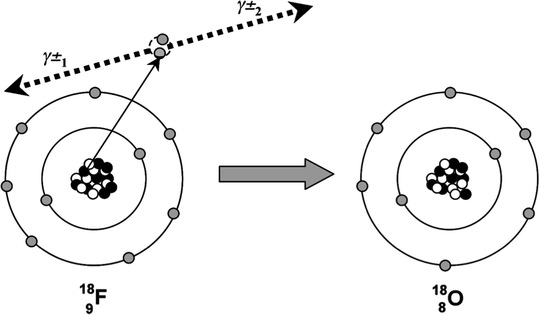
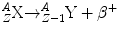
Fig. 4.6
The radioactive decay of 18F by positron emission is shown. The emitted positron annihilates with an electron in the surrounding environment and two annihilation photons(γ±) are emitted
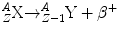
Particulate Radiation
Particle emission from radioactive decay was the first observation of natural radioactivity. Wilhelm Röntgen had produced X-rays in 1896, and a year later, Henri Becquerel showed that naturally occurring uranium produced radiation spontaneously. While the radiation was thought initially to be similar to Röntgen’s X-rays, Lord Rutherford showed that some types of radiation were more penetrating than others. He called the less penetrating radiation alpha (α) rays and the more penetrating ones beta (β) rays. Soon after it was shown that these radiations could be deflected by a magnetic field, that is, they carried charge. It was clear that these were not electromagnetic rays and were, in fact, particles.
Alpha Radiation (α)
Alpha particles are emitted from large nuclei, often as part of a radioactive series (e.g., thorium series, radium series). An α particle consists of two protons and two neutrons and thus is identical to a doubly ionized helium atom. For this reason, it is often written as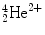
. Alpha decay results in a daughter nuclide with an atomic number of 2 less than the parent nuclide and a mass number of 4 less. The equation for α decay is
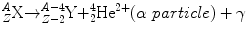
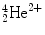. Alpha decay results in a daughter nuclide with an atomic number of 2 less than the parent nuclide and a mass number of 4 less. The equation for α decay is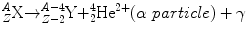Over the last several years, researchers have taken an interest in the use of α-particle-emitting radionuclides attached to tumor-specific targeting agents, such as antibodies. The advantage of α particles for targeted radionuclide therapy is their high energy (5–9 MeV) and short range (50–90 μm) resulting in a high density of local energy deposition close to the decay site. Therefore, α-emitters are especially suited to the treatment of disseminated cancers such as leukemias or micrometastatic disease. In addition, the greater rate of the energy loss per unit track length, referred to as the linear energy transfer (LET), results in a greater radiobiological effectiveness for cell kill for α particles relative to β and photon (low LET) radiations. Radiation dose estimates to normal tissues for α-particle-emitting radionuclides can be made (if imaging data resulting from concomitant X- or γ-rays emitted has been obtained) using the Medical International Radiation Dose (MIRD) committee assumption of total local absorption for non-penetrating radiations. However, the calculated organ and tissue doses need to be accepted with the following caveats: (a) at low doses, the stochastic nature of energy deposition must be considered, that is, an average dose of 0.2 Gy is the consequence of a Poisson distribution of cellular hits in which some cell nuclei receive α-particle hits, while others receive no hits; (b) the microdistribution of the agent may be non-homogenously distributed with respect to the biological organ or structure, for example, radium bone-seeking agents may deposit on bone surface, leading to high doses at the marrow–bone interface with zero dose to the central marrow regions; and (c) the selective uptake or accumulation of α-emitters to cells can result in local doses that greatly exceed the average tissue dose.
Although not common, α-particle-emitting radionuclides have begun to be employed in the clinic. Current indications include 213Bi (and 225Ac)-labeled M195 antibody against leukemia, 211At-anti-tenascin antibody against brain tumors, 223Ra-chloride as a therapy for bone metastases, and 211At-methylene blue for melanoma.
Beta Radiation (β−)
Beta-minus particles are emitted from neutron-rich nuclei, and this is done in an attempt to approach the line of nuclear stability in terms of the relative number of protons and neutrons within the atomic nucleus. A β − particle consists of an electron ejected from the nucleus after a neutron is converted into a proton. The β − is ejected so that charge is conserved during this transformation. Beta-minus decay results in a daughter nuclide with an atomic number of one greater than the parent nuclide and a mass number which is unchanged. Beta-minus particles have a continuous range of energies up to a maximum. This appeared at first to be a violation of the conservation of energy. To overcome this problem, in 1931 Wolfgang Pauli proposed that another particle was emitted which he called the neutrino (ν). He suggested that this particle had a very small mass and zero charge. It could carry away the excess momentum to account for the difference between the maximum beta energy and the spectrum of energies that the emitted beta particles displayed. In fact, we now refer to the neutrino emitted in beta-minus decay as the anti-neutrino, indicated by the “¯” over the symbol ν.
The equation for β − decay is
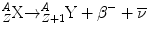
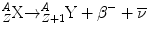
The nucleus of the daughter nuclide is often left in an excited state with excess energy, and therefore, this energy is often emitted in the form of a gamma ray after β− decay.
The following shows an example of a beta decay scheme for 131I:
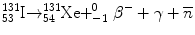
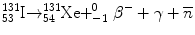
The half-life for 131I decay is 8.02 days. The most abundant β− particle emitted has a maximum energy of 0.606 MeV, and there are many associated γ-rays, the most abundant (branching ratio = 0.81) having an energy of 0.364 MeV.
β− Dosimetry
The most commonly used radionuclide for nuclear medicine therapies is 131I, which is used for the treatment of a variety of thyroid disorders, benign and malignant, as well as for a several therapeutic radiolabeled antibody therapies such as 131I-tositumomab (Bexxar®) for the treatment of follicular, non-Hodgkin’s lymphoma. The pure β− emitter 90Y has also become routinely used for radioimmunotherapy applications, for example, ibritumomab tiuxetan (Zevalin) for the treatment of B cell non-Hodgkin’s lymphoma. The use of 90Y-microspheres (SIR-Spheres, Sirtex Medical Inc.) has also emerged as a new intra-arterial therapy for the treatment of hepatocellular carcinoma (HCC) and potentially other diseases metastatic to liver. An advantage of 90Y is the extremely low yield of penetrating photon emissions (only Bremsstrahlung radiation) facilitating the handling of large activities and resulting in lower radiation exposures to personnel within proximity of the patients. However, the lack of g photons for imaging can be a disadvantage when using 90Y radiopharmaceuticals, and therefore, to verify safety of delivery, protocols usually incorporate a pre-scan using an alternative-labeled agent. It has recently emerged, however, that the extremely small positron emission fraction from 90Y (∼32 p.p.m.) can be imaged using later-generation PET scanners and this is now being pursued by many research groups. Another β−-emitting radionuclide in increasing clinical use is 188Re. This radionuclide has the advantage that it is produced from a tungsten-188 generator system, making it more readily available for use in developing nations, without access to radionuclide production facilities. 188Re-lipiodol is an alternative to 90Y-microspheres for the treatment of HCC and has the advantage of allowing imaging (using the 155 keV γ – 15% abundance)-based treatment planning. The average β− emission energy is high at 795 keV, comparable to the 935 keV of 90Y.
The dose versus distance for a point source of beta particles obeys the relationship first described by Loevinger [1], which consists of an inverse square geometric term and a power term to account for absorption. The dose from a point source therefore falls more sharply than the inverse square law. However, for distributed sources as in most medical applications of radiopharmaceuticals employing β− sources, the dose is often fairly uniform within most organ structures. The MIRD methodology classifies all β− particles as non-penetrating radiations that are deposited locally within the source organ, that is, cross-fire between different organs is considered to be negligible. A detailed discussion of the heterogeneity of β−-emitting radiopharmaceuticals and the dosimetric implications is provided in ICRP Report 67 [2].
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
