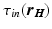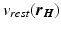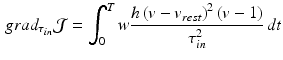(1)
where
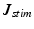 represents the initial stimulus,
represents the initial stimulus, 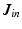 and
and 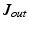 denotes the sum of all inward and outward currents, respectively, which are defined as
denotes the sum of all inward and outward currents, respectively, which are defined as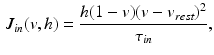
(2)
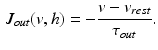
(3)
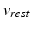 is the resting potential. This parameter was not considered in the original formulation. It was incorporated in [1] to simulate the increase of the resting potential during ischemia.
is the resting potential. This parameter was not considered in the original formulation. It was incorporated in [1] to simulate the increase of the resting potential during ischemia.The gating variable h(t) is dimensionless and varies between zero and one. This variable regulates inward current flows and obeys the following equation
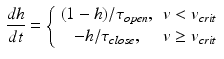
where 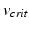 is the change-over voltage. This model contains four time constants (
is the change-over voltage. This model contains four time constants (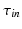 ,
, 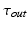 ,
,  and
and 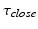 ) which correspond to the four phases of the cardiac action potential: initiation, plateau, decay and recovery (see [1] for details).
) which correspond to the four phases of the cardiac action potential: initiation, plateau, decay and recovery (see [1] for details).
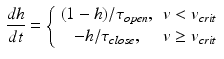
(4)
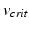 is the change-over voltage. This model contains four time constants (
is the change-over voltage. This model contains four time constants (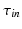 ,
, 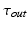 ,
,  and
and 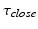 ) which correspond to the four phases of the cardiac action potential: initiation, plateau, decay and recovery (see [1] for details).
) which correspond to the four phases of the cardiac action potential: initiation, plateau, decay and recovery (see [1] for details).The effects of ischemia are simulated by modifying the values of 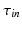 and
and 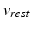 [4]. For ischemic cells, we set the parameter
[4]. For ischemic cells, we set the parameter 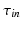 and
and 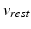 equal to
equal to 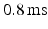 and 0.1, respectively. For healthy cells
and 0.1, respectively. For healthy cells 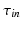 and
and 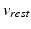 are set to
are set to 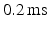 and 0, respectively.
and 0, respectively.
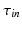 and
and 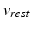 [4]. For ischemic cells, we set the parameter
[4]. For ischemic cells, we set the parameter 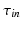 and
and 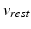 equal to
equal to 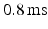 and 0.1, respectively. For healthy cells
and 0.1, respectively. For healthy cells 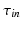 and
and 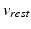 are set to
are set to 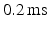 and 0, respectively.
and 0, respectively.2.2 Cardiac Tissue Model
Let 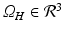 be the cardiac tissue, and
be the cardiac tissue, and 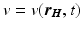 the membrane potential with
the membrane potential with 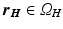 . The propagation of v is described according to the monodomain formalism,
. The propagation of v is described according to the monodomain formalism,
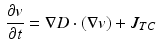
where 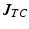 is the ion current term current provided by TC model, and D is the intracellular conductivity tensor (assumed constant
is the ion current term current provided by TC model, and D is the intracellular conductivity tensor (assumed constant 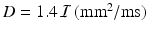 ). Equation (5) is solved by imposing the initial conditions
). Equation (5) is solved by imposing the initial conditions 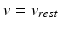 at
at 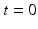 , and no-flux boundary conditions.
, and no-flux boundary conditions.
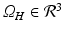 be the cardiac tissue, and
be the cardiac tissue, and 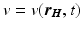 the membrane potential with
the membrane potential with 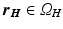 . The propagation of v is described according to the monodomain formalism,
. The propagation of v is described according to the monodomain formalism,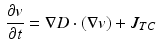
(5)
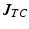 is the ion current term current provided by TC model, and D is the intracellular conductivity tensor (assumed constant
is the ion current term current provided by TC model, and D is the intracellular conductivity tensor (assumed constant 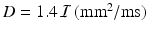 ). Equation (5) is solved by imposing the initial conditions
). Equation (5) is solved by imposing the initial conditions 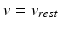 at
at 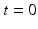 , and no-flux boundary conditions.
, and no-flux boundary conditions.2.3 Model of Remote Recordings
According to the Volumen Conductor Theory [13, 16], the resulting potential distribution at position 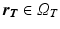 outside the cardiac tissue
outside the cardiac tissue 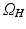 , is calculated as
, is calculated as
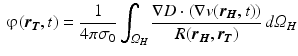
where 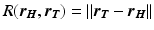 represents the distance from the source location point
represents the distance from the source location point 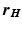 to the observation point
to the observation point 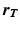 ,
, 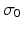 is the medium conductivity (assumed homogeneous and set to 1
is the medium conductivity (assumed homogeneous and set to 1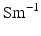 ), and
), and 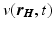 is solution of (5). Equations (1)–(6) comprise a complete description of the forward problem.
is solution of (5). Equations (1)–(6) comprise a complete description of the forward problem.
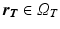 outside the cardiac tissue
outside the cardiac tissue 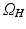 , is calculated as
, is calculated as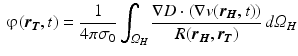
(6)
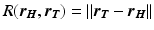 represents the distance from the source location point
represents the distance from the source location point 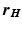 to the observation point
to the observation point 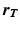 ,
,  is the medium conductivity (assumed homogeneous and set to 1
is the medium conductivity (assumed homogeneous and set to 1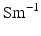 ), and
), and 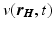 is solution of (5). Equations (1)–(6) comprise a complete description of the forward problem.
is solution of (5). Equations (1)–(6) comprise a complete description of the forward problem.3 Inverse Procedure
Let 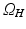 be a synthetic cardiac tissue which contains an ischemic region, and
be a synthetic cardiac tissue which contains an ischemic region, and 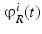 be a set of associated remote measurements. Note that
be a set of associated remote measurements. Note that 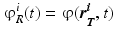 with
with ![$$t\in [0,T]$$](/wp-content/uploads/2016/09/A339585_1_En_45_Chapter_IEq38.gif) and
and 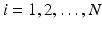 , being T the total recording time, and N the number of recording points. Hereinafter, we assume that the regional ischemia constitute our true ischemic configuration, and
, being T the total recording time, and N the number of recording points. Hereinafter, we assume that the regional ischemia constitute our true ischemic configuration, and 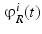 is our observed data.
is our observed data.
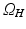 be a synthetic cardiac tissue which contains an ischemic region, and
be a synthetic cardiac tissue which contains an ischemic region, and 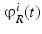 be a set of associated remote measurements. Note that
be a set of associated remote measurements. Note that 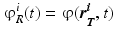 with
with ![$$t\in [0,T]$$](/wp-content/uploads/2016/09/A339585_1_En_45_Chapter_IEq38.gif) and
and 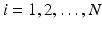 , being T the total recording time, and N the number of recording points. Hereinafter, we assume that the regional ischemia constitute our true ischemic configuration, and
, being T the total recording time, and N the number of recording points. Hereinafter, we assume that the regional ischemia constitute our true ischemic configuration, and 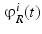 is our observed data.
is our observed data.The aim of the inverse procedure is to estimate the shape and the location of the ischemic areas by adjusting the spatial distribution of 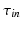 and
and 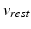 . This is achieved by minimizing the misfit between the observed data
. This is achieved by minimizing the misfit between the observed data 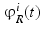 , and the data associated to a guess configuration:
, and the data associated to a guess configuration: 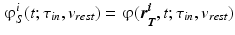 . We use an iterative scheme in which the following cost functional
. We use an iterative scheme in which the following cost functional
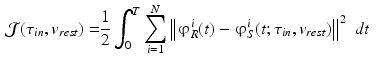
is reduced at each step of the reconstruction process. We use an adjoint formulation to find a direction in the parameter space 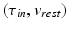 such that the cost functional decreases. The ischemic region is defined by a level set function [1].
such that the cost functional decreases. The ischemic region is defined by a level set function [1].
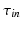 and
and 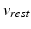 . This is achieved by minimizing the misfit between the observed data
. This is achieved by minimizing the misfit between the observed data 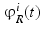 , and the data associated to a guess configuration:
, and the data associated to a guess configuration: 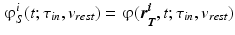 . We use an iterative scheme in which the following cost functional
. We use an iterative scheme in which the following cost functional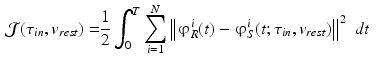
(7)
 such that the cost functional decreases. The ischemic region is defined by a level set function [1].
such that the cost functional decreases. The ischemic region is defined by a level set function [1].Since both parameters, 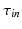 and
and 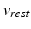 , define the same region, we only consider the variation of
, define the same region, we only consider the variation of 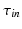 for the gradient computation. Following [1], the gradient of the function
for the gradient computation. Following [1], the gradient of the function 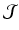 over the parameter
over the parameter 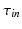 is given by
is given by
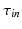 and
and 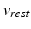 , define the same region, we only consider the variation of
, define the same region, we only consider the variation of 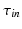 for the gradient computation. Following [1], the gradient of the function
for the gradient computation. Following [1], the gradient of the function 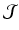 over the parameter
over the parameter 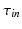 is given by
is given by