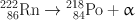Fig. 2.1
Isometric transition of 99mTc. Ten percent of the decay follows internal conversion.
Gamma (γ)-Ray Emission
The common mode of an isomeric transition from an upper energy state of a nucleus to a lower energy state is by emission of an electromagnetic radiation, called the γ-ray . The energy of the γ-ray emitted is the difference between the two isomeric states. For example, a decay of a 525-keV isomeric state to a 210-keV isomeric state will result in the emission of a 315-keV γ-ray.
Internal Conversion
An alternative to the γ-ray emission is the internal conversion process . The excited nucleus transfers the excitation energy to an orbital electron—preferably the K-shell electron—of its own atom, which is then ejected from the shell, provided the excitation energy is greater than the binding energy of the electron (Fig. 2.2). The ejected electron is called the conversion electron and carries the kinetic energy equal to E γ – E B , where E γ is the excitation energy and E B is the binding energy of the electron. Even though the K-shell electrons are more likely to be ejected because of the proximity to the nucleus, the electrons from the L shell, M shell, and so forth also may be ejected by the internal conversion process. The ratio of the number of conversion electrons (N e ) to the number of observed γ-radiations (N γ ) is referred to as the conversion coefficient, given as α = N e /N γ . The conversion coefficients are subscripted as α K , α L , α M … depending on which shell the electron is ejected from. The total conversion coefficient α T is then given by
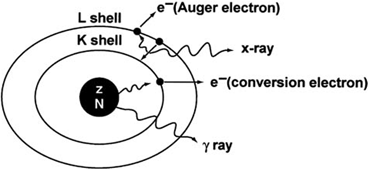

Fig. 2.2
Internal conversion process. The excitation energy of the nucleus is transferred to a K-shell electron, which is then ejected with kinetic energy equal to E γ –E B , and the K-shell vacancy is filled by an electron from the L shell. The energy difference between the L shell and K shell appears as the characteristic K x-ray. Alternatively, the characteristic K x-ray may transfer its energy to an L-shell electron, called the Auger electron, which is then ejected.
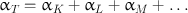
An internal conversion process leaves an atom with a vacancy in one of its shells, which is filled by an electron from the next higher shell. Such situations may also occur in nuclides decaying by electron capture (see later). When an L electron fills in a K-shell vacancy, the energy difference between the K shell and the L shell appears as a characteristic K x-ray. Alternatively, this transition energy may be transferred to an orbital electron, which is emitted with a kinetic energy equal to the characteristic x-ray energy minus its binding energy. These electrons are called Auger electrons , and the process is termed the Auger process , analogous to internal conversion. The Auger electrons are monoenergetic. Because the characteristic x-ray energy (energy difference between the two shells) is always less than the binding energy of the K-shell electron, the latter cannot undergo the Auger process and cannot be emitted as an Auger electron .
The vacancy in the shell resulting from an Auger process is filled by the transition of an electron from the next upper shell, followed by emission of similar characteristic x-rays and/or Auger electrons . The fraction of vacancies in a given shell that are filled by emitting characteristic x-ray emissions is called the fluorescence yield , and the fraction that is filled by the Auger processes is the Auger yield. The Auger process increases with the increasing atomic number of the atom.
Problem 2.1
If the total conversion coefficient (α T ) is 0.11 for the 140-keV γ-rays of 99mTc, calculate the percentage of 140-keV γ-radiations available for imaging.
Answer
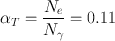
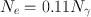
Total number of disintegrations
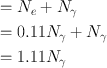
Thus, the percentage of γ-radiations
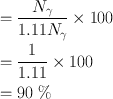
Alpha (α)-Decay
The α-decay occurs mostly in heavy nuclides such as uranium, radon, plutonium, and so forth. Beryllium-8 is the only lightest nuclide that decays by breaking up into two α-particles. The α-particles are basically helium ions with two protons and two neutrons in the nucleus and two electrons removed from the orbital of the helium atom. After α-decay, the atomic number of the nucleus is reduced by 2 and the mass number by 4.