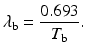(1)
Cleveland Clinic, Emeritus Staff, Cleveland, OH, USA
Keywords
Atomic structureNuclear structureRadioactive decayDecay equation γ Ray interactionAttenuationAtomic Structure
Matter is composed of atoms. An atom consists of a nucleus containing protons (Z) and neutrons (N), collectively called nucleons, and electrons rotating around the nucleus. The sum of neutrons and protons (total number of nucleons) is the mass number denoted by A. The properties of neutrons, protons, and electrons are listed in Table 1.1. The number of electrons in an atom is equal to the number of protons (atomic number Z) in the nucleus. The electrons rotate along different energy shells designated as K-shell, L-shell, M-shell, etc. (Fig. 1.1). Each shell further consists of subshells or orbitals, e.g., the K-shell has s orbital; the L-shell has s and p orbitals; the M-shell has s, p, and d orbitals, and the N-shell has s, p, d, and f orbitals. Each orbital can accommodate only a limited number of electrons. For example, the s orbital contains up to 2 electrons; the p orbital, 6 electrons; the d orbital, 10 electrons; and the f orbital, 14 electrons. The capacity number of electrons in each orbital adds up to give the maximum number of electrons that each energy shell can hold. Thus, the K-shell contains 2 electrons; the L-shell 8 electrons, the M-shell 18 electrons, and so forth.
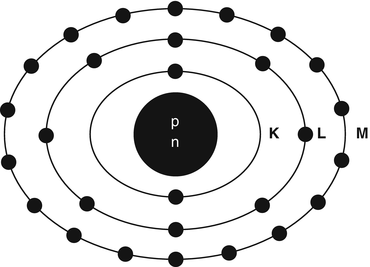
Table 1.1
Characteristics of electrons and nucleons
Particle | Charge | Mass (amu)a | Mass (kg) | Mass (MeV)b |
|---|---|---|---|---|
Electron | −1 | 0.000549 | 0.9108 × 10−30 | 0.511 |
Proton | +1 | 1.00728 | 1.6721 × 10−27 | 938.78 |
Neutron | 0 | 1.00867 | 1.6744 × 10−27 | 939.07 |

Fig. 1.1
Schematic structure of a 28Ni atom. The nucleus containing protons and neutrons is at the center. The K-shell has 2 electrons, the L-shell 8 electrons, and the M-shell 18 electrons
A combination of a given number of protons and neutrons in a nucleus leads to an atom called the nuclide. A nuclide X is represented by Z A X N . Some nuclides (280 or so) are stable, while others (more than 3400) are unstable. The unstable nuclides are termed the radionuclides, most of which are artificially produced in the cyclotron or reactor, with a few naturally occurring. The nuclides having the same number of protons are called the isotopes, e.g., 12 6C6 and 13 6C7; the nuclides having the same number of neutrons are called the isotones, e.g., 16 8O8 and 15 7N8; the nuclides having the same mass number are called the isobars, e.g., 131I and 131Xe; and the nuclides with the same mass number but differing in energy are called the isomers, e.g., 99mTc and 99Tc.
Radioactive Decay
Radionuclides are unstable due to the unsuitable composition of neutrons and protons or excess energy and, therefore, decay by emission of radiations such as α particles, β − particles, β + particles, electron capture, and isomeric transition.
α Decay
This decay occurs in heavy nuclei such as 235U and 239Pu. For example,
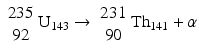
Alpha particles are a nucleus of helium atom 24He2 having two protons and two neutrons in the nucleus with two orbital electrons stripped off from the K-shell. The α particles are emitted with discrete energy and have a very short range in matter, e.g., about 0.03 mm in human tissues.
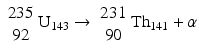
(1.1)
β− Decay
β – Decay occurs in radionuclides that are neutron rich. In the process, a neutron in the nucleus is converted to a proton along with the emission of a β − particle and an antineutrino, 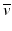 .
.
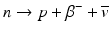
For example,
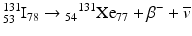 The energy difference between the two nuclides (i.e., between 131I and 131Xe in the above example) is called the decay energy or transition energy, which is shared between the β − particle and the antineutrino
The energy difference between the two nuclides (i.e., between 131I and 131Xe in the above example) is called the decay energy or transition energy, which is shared between the β − particle and the antineutrino 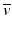 . Because of the random nature of decay, β − particles are emitted with a spectrum of energy with the transition energy as the maximum energy and with an average energy equal to one-third of the maximum energy.
. Because of the random nature of decay, β − particles are emitted with a spectrum of energy with the transition energy as the maximum energy and with an average energy equal to one-third of the maximum energy.
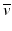 .
.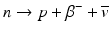
(1.2)
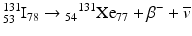
 . Because of the random nature of decay, β − particles are emitted with a spectrum of energy with the transition energy as the maximum energy and with an average energy equal to one-third of the maximum energy.
. Because of the random nature of decay, β − particles are emitted with a spectrum of energy with the transition energy as the maximum energy and with an average energy equal to one-third of the maximum energy.Positron (β+) Decay
When a radionuclide is proton rich, it decays by the emission of a positron (β +) along with a neutrino v. In essence, a proton in the nucleus is converted to a neutron in the process.
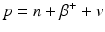
Since a neutron is one electron mass heavier than a proton, the right-hand side of Eq. (1.3) is two electron mass more than the left-hand side, i.e., 2 × 0.511 MeV = 1.022 MeV more on the right side. For conservation of energy, therefore, the radionuclide must have a transition energy of at least 1.022 MeV to decay by β + emission. The energy beyond 1.022 MeV is shared as kinetic energy by the β + particle and the neutrino.
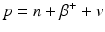
(1.3)
Some examples of positron-emitting nuclides are:
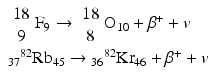 Positron emission tomography (PET) is based on the principle of coincidence detection of the two 511-keV photons arising from positron emitters, which will be discussed in detail later.
Positron emission tomography (PET) is based on the principle of coincidence detection of the two 511-keV photons arising from positron emitters, which will be discussed in detail later.
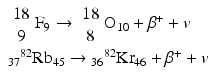
Electron Capture
When a radionuclide is proton rich, but has energy less than 1.022 MeV, then it decays by electron capture. In the process, an electron from the nearest shell, i.e., K-shell, is captured by a proton in the nucleus to produce a neutron, and a neutrino v is emitted to conserve energy.
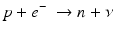
Note that when the transition energy is less than 1.022 MeV, the radionuclide definitely decays by electron capture. However, when the transition energy is more than 1.022 MeV, the radionuclide can decay by positron emission and/or electron capture. The greater the transition energy above 1.022 MeV, the more likely the radionuclide will decay by positron emission. Some examples of radionuclides decaying by electron capture are:
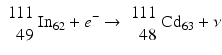
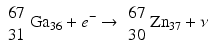
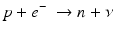
(1.4)
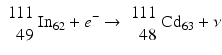
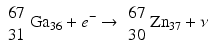
Isomeric Transition
When a nucleus has excess energy above the ground state, it can exist in excited (energy) states, which are called the isomeric states. The lifetimes of these states normally are very short (~10−15 to 10−12 s); however, in some cases, the lifetime can be longer from minutes to years. When an isomeric state has a longer lifetime, it is called a metastable state and is represented by “m.” Thus, having an energy state of 140 keV above 99Tc and decaying with a half-life of 6 h, 99mTc is an isomer of 99Tc.
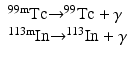 A radionuclide may decay by α, β −, β + emissions, or electron capture to different isomeric states of the product nucleus, if allowed by the rules of quantum physics. Naturally, these isomeric states decay to lower isomeric states and finally to the ground states of the product nucleus, and the energy differences appear as γ-ray photons.
A radionuclide may decay by α, β −, β + emissions, or electron capture to different isomeric states of the product nucleus, if allowed by the rules of quantum physics. Naturally, these isomeric states decay to lower isomeric states and finally to the ground states of the product nucleus, and the energy differences appear as γ-ray photons.
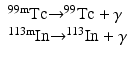
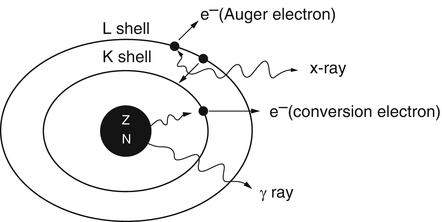
As an alternative to γ-ray emission, the excitation energy may be transferred to an electron, preferably in the K-shell, which is then ejected with energy 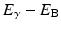 , where E γ and E B are the γ-ray energy and binding energy of the electron, respectively (Fig. 1.2). This process is called the internal conversion, and the ejected electron is called the conversion electron. The vacancy created in the K-shell is filled by the transition of an electron from an upper shell. The energy difference between the two shells appears as a characteristic K X-ray. Similarly, characteristic L X-ray and M X-ray can be emitted if the vacancy in the L- or M-shell is filled by electron transition from upper shells. Like γ rays, the characteristic X-ray energy can be emitted as photons or be transferred to an electron in a shell which is then ejected, if energetically possible. The latter is called the Auger process, and the ejected electron is called the Auger electron.
, where E γ and E B are the γ-ray energy and binding energy of the electron, respectively (Fig. 1.2). This process is called the internal conversion, and the ejected electron is called the conversion electron. The vacancy created in the K-shell is filled by the transition of an electron from an upper shell. The energy difference between the two shells appears as a characteristic K X-ray. Similarly, characteristic L X-ray and M X-ray can be emitted if the vacancy in the L- or M-shell is filled by electron transition from upper shells. Like γ rays, the characteristic X-ray energy can be emitted as photons or be transferred to an electron in a shell which is then ejected, if energetically possible. The latter is called the Auger process, and the ejected electron is called the Auger electron.
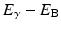 , where E γ and E B are the γ-ray energy and binding energy of the electron, respectively (Fig. 1.2). This process is called the internal conversion, and the ejected electron is called the conversion electron. The vacancy created in the K-shell is filled by the transition of an electron from an upper shell. The energy difference between the two shells appears as a characteristic K X-ray. Similarly, characteristic L X-ray and M X-ray can be emitted if the vacancy in the L- or M-shell is filled by electron transition from upper shells. Like γ rays, the characteristic X-ray energy can be emitted as photons or be transferred to an electron in a shell which is then ejected, if energetically possible. The latter is called the Auger process, and the ejected electron is called the Auger electron.
, where E γ and E B are the γ-ray energy and binding energy of the electron, respectively (Fig. 1.2). This process is called the internal conversion, and the ejected electron is called the conversion electron. The vacancy created in the K-shell is filled by the transition of an electron from an upper shell. The energy difference between the two shells appears as a characteristic K X-ray. Similarly, characteristic L X-ray and M X-ray can be emitted if the vacancy in the L- or M-shell is filled by electron transition from upper shells. Like γ rays, the characteristic X-ray energy can be emitted as photons or be transferred to an electron in a shell which is then ejected, if energetically possible. The latter is called the Auger process, and the ejected electron is called the Auger electron.
Fig. 1.2
γ-Ray emission and internal conversion process. In internal conversion process, the excitation energy of the nucleus is transferred to a K-shell electron, which is then ejected, and the K-shell vacancy is filled by an electron from the L-shell. The energy difference between the L-shell and K-shell appears as the characteristic K X-ray. The characteristic K X-ray energy may again be transferred to an L-shell electron, which is then ejected in the Auger process
The decay of radionuclides is represented by a decay scheme, an example of which is given for 68Ga in Fig. 1.3.
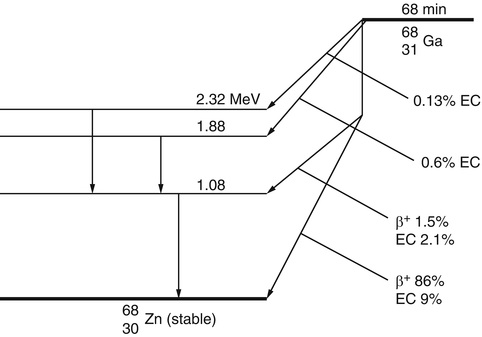

Fig. 1.3
The decay scheme of 68Ga. The 87.5% of positrons are annihilated to give rise to 175% of 511-keV photons
Radioactive Decay Equations
General Decay Equations
The atoms of a radioactive sample decay randomly, and one cannot tell which atom will decay when. One can only talk about an average decay of the atoms in the sample. This decay rate is proportional to the number of radioactive atoms present. Mathematically,
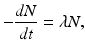
where –dN/dt is the rate of decay denoted by the term activity or radioactivity A, λ is the decay constant, and N is the number of atoms of the radionuclide present. Thus,
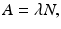
Integrating Eq. (1.5) gives the activity A t at time t as
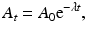
where A 0 is the activity at time t = 0. The plot of A t vs. t on a semilog scale is shown in Fig. 1.4. If one knows activity A 0 at a given time, the activity A t at time t before or later can be calculated by Eq. (1.7).
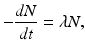
(1.5)
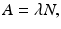
(1.6)
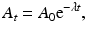
(1.7)

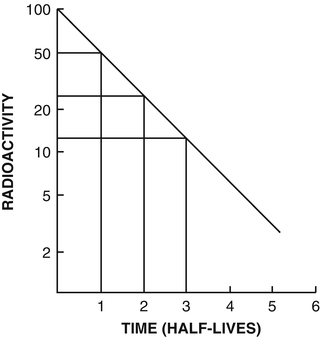
Fig. 1.4
Plot of activity A t against time on a semilogarithmic graph indicating a straight line. The slope of the line is the decay constant λ of the radionuclide. The half-life t 1/2 is calculated from λ using (1.8). Alternatively, the half-life is determined by reading an initial activity and half its value and their corresponding times. The difference in time between the two readings is the half-life
Half–life (t 1∕2): The half-life of a radionuclide is defined as the time required to reduce the initial activity to one-half. It is unique for every radionuclide and is related to the decay constant as follows:
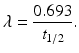
The half-life of a radionuclide is determined by measuring the radioactivity at different time intervals and plotting them on semilogarithmic paper, as shown in Fig. 1.4. An initial activity and half its value are read from the straight line, and the corresponding times are noted. The difference in time between the two readings gives the half-life of the radionuclide.
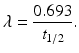
(1.8)
The mean life τ of a radionuclide is defined by
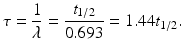
A radionuclide decays by 63% in one mean life.
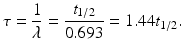
(1.9)
Effective half–life: Each radionuclide decays with a definite half-life, called the physical half-life, which is denoted by T p or t 1∕2. When radiopharmaceuticals are administered to patients, analogous to physical decay, they are eliminated from the body by biological processes such as fecal excretion, urinary excretion, and perspiration. This elimination is characterized by a biological half-life (T b) which is defined as the time taken to eliminate a half of the administered activity from the biological system. It is related to the decay constant λ b by