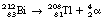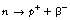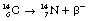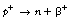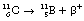Chapter 19 Radioactivity

19.1 Aim

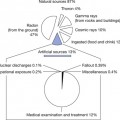
The aim of this chapter is to discuss the various types of radioactive decay which can occur. Within the chapter the relevance of these processes to nuclear medicine will be considered.

19.2 Introduction

Chapter 18 referred to various terms which may be used to define nuclear structure. This chapter will examine the changes which may take place in the nucleus during radioactive decay.

The term radioactive is applied to nuclei which are unstable. In these nuclei, the forces disrupting the nucleus are stronger than the forces which hold the nucleus together. The instability of the nucleus is demonstrated by the fact that it changes its internal structure to a more stable form, often (but not always) ejecting a charged particle from the nucleus in the process. Each time a nucleus changes its structure it is called a radioactive disintegration or a nuclear transformation and may result in a change in the atomic number – number of protons in the nucleus – (and therefore element) or a change in the mass number – number of protons and neutrons in the nucleus – or a change of both the atomic number and the mass number.

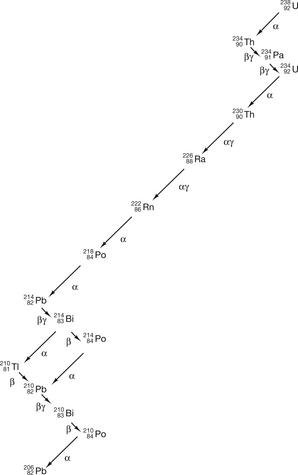
A pictorial representation of the decay process (see Fig. 19.1) is called a decay scheme. In addition to this, it is possible for a nucleus to undergo more than one type of transformation (see Fig. 19.12 later in this chapter) and this type of decay is called a branching scheme.

Figure 19.1 The uranium decay series. Note that arrows to the right indicate an increase in the atomic number while arrows to the left indicate a decrease. The downward direction of the arrows indicates that the nucleus loses energy with each transformation (downward direction not drawn to scale).

It is impossible to determine the exact time when a particular nucleus will transform, but the laws of probability may be used to determine the behaviour of a large number of nuclei (see Ch. 20 for a discussion of radioactive decay and the exponential law).

The unit of radioactivity is the becquerel (Bq) where 1 becquerel is 1 nuclear disintegration per second.

Insight

Before the introduction of International System of Units (SI) units, radioactivity was measured in curie (Ci). 1 curie was equal to 3.7×10¹⁰ nuclear disintegrations per second. Thus, an activity of 1 Ci is the same as an activity of 3.7−10¹⁰ Bq or 37 GBq. From this it can be seen that the curie was a much larger unit than the becquerel.

It is often useful to know the specific activity of a sample. This is the activity of radionuclide per unit mass of the sample and so is measured in Bq.kg⁻¹ or submultiples thereof.

19.3 Nuclide chart

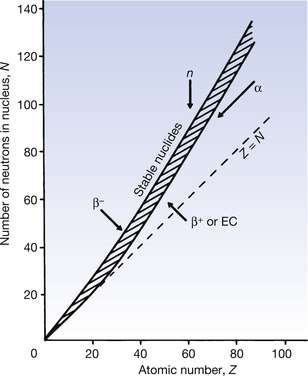
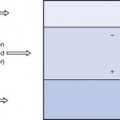
It is often useful to draw a graph, plotting the number of neutrons in a nucleus against the number of protons, as all nuclides may be included in this nuclide chart. Such a chart is shown in simplified form in Figure 19.2. Note that isotopes (lines of equal atomic number) are given by any vertical line on the figure. In such a graph, an angle of 45° to the x-axis represents a situation where the nucleus contains equal numbers of protons and neutrons (Z=N).

Figure 19.2 A graph of the neutron number (N) plotted against the atomic number (Z) showing the position of the stable nuclides as a shaded band. Note that, as the atomic number increases, a higher proportion of neutrons to protons is required to achieve stability. Also shown are the directions which a nucleus takes for various forms of radioactive decay (these movements are not to scale). EC, electron capture.

It is found on such a graph that there is a broad band of nuclides with low atomic numbers at about 45° to the x-axis and these are all stable or only weakly radioactive. Thus, for the lighter elements, nuclear stability can be produced with equal numbers of protons and neutrons. From the graph it can be seen that, as the atomic number increases, a proportionately larger number of neutrons is necessary to produce nuclear stability. Thus we can say that as the Coulomb repulsion (see Sect. 6.4) between the protons increases, then more neutrons are required to produce the short-range nuclear forces (see Sect. 18.3.1), thus producing the cohesive forces required for a stable nucleus. Nuclei which have atomic numbers greater than 83 (bismuth) are so large that it is impossible to produce a stable nuclear configuration.

Nuclides whose combination of neutrons and protons means that they land outside the band of stability shown in Figure 19.2 have nuclei possessing higher energies than those within the band. As a consequence, such a nucleus is unstable and tends, on decay, to produce a new nucleus of lower energy which is closer to, or within, the stable band. The energy difference between the nucleus before and after decay is emitted either as a charged particle or as a quantum (or quanta) of electromagnetic radiation. The decay scheme towards stability may be in the form of a single step (e.g. 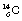decays to stable 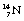¹ by the emission of a beta-particle (see Fig. 19.4) or it may be in the form of a multistage route involving many nuclear transformations (e.g. the decay of 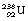to 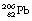involves at least 14 steps, as shown in Figure 19.1). As a general rule, the greater the mass number of the nuclide, the more complicated the decay path to eventual stability.

The effect of different decay modes is illustrated using arrows on Figure 19.2 The direction of the arrow shows the direction of change of position on the chart before and after the decay process. You may find it helpful to refer back to this chart while studying the decay processes in more detail in the following sections of this chapter.

19.4 Alpha decay or alpha-particle emission

For the spontaneous emission of an alpha-particle from a nucleus, the nuclide must have an atomic mass number greater than 150. The nucleus must also have too few neutrons for the number of protons – a higher neutron-to-proton ratio would be required to produce nuclear stability. The alpha-particle consists of two protons and two neutrons tightly bound together (a helium nucleus). It may be considered as a free particle having high kinetic energy which is trapped in the parent nucleus. Thus the daughter nucleus has two protons and two neutrons fewer than the parent nucleus (see Equation 19.1 below).

The mechanism of production of the alpha-particle is quite complex. As we have already identified (see Sect. 18.3.1), the nucleus depends on a balance of disruptive electrostatic (Coulomb) forces and attractive forces between the nucleons caused by the short-range nuclear forces. In very large nuclei there is a large amount of electrostatic repulsion between the protons which extends across the whole nucleus. This is balanced by the short-range nuclear force which exists between adjacent nucleons. Thus, if the nucleus becomes elongated, the electrostatic forces dominate and the nucleus becomes even more elongated. This process continues until the nucleus divides into two fragments, the daughter nuclide and the alpha-particle.

An example of alpha-decay is the decay of bismuth-212 to thallium-208 with the emission of alpha-particles. This process is shown in the following equation:

Equation 19.1

Note that there is a reduction of four in the atomic mass number and two in the atomic number between parent and daughter product.

This reaction can also be written as shown in Figure 19.3 (the decay of 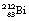also includes the emission of a beta-particle and is discussed later as an example of a branching programme; for simplicity only the alpha-particle reaction is shown in Fig. 19.3 and the percentages shown refer only to the alpha-particles). Because the daughter product is to the left of the parent nuclide, this shows that there is a reduction in the atomic number. The reaction also shows that the difference in energy between the parent nuclide and the daughter nuclide is 6.08 MeV. If we consider only the alpha-particles emitted, we find that approximately 71% of these have an energy of 6.04 MeV and 29% have an energy of 6.08 MeV. In the case of the first group of alpha-particles, the nucleus is left in an excited state with excess energy of 0.04 MeV which it emits as a gamma-ray.

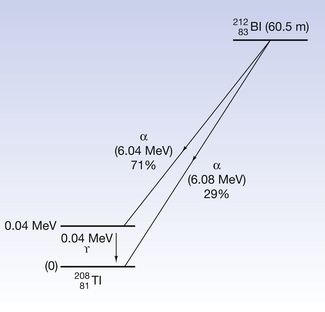
Figure 19.3 An example of alpha-particle emission. The nucleus decreases its atomic number and energy as shown.

The ejection of an alpha-particle means that, to preserve momentum, the nucleus must also recoil with an equal and opposite momentum to that of the alpha-particle. The energy of the recoiling nucleus is typically about 2% of that of the emitted alpha-particle. (Recoil also exists for beta-decay but is much smaller due to the tiny mass of the beta-particle.)

Alpha-particles are intensely ionizing but have a very short range in tissue so have little practical application in radiology.

19.5 Beta decay or beta-particle emission

In the process of beta decay, a particle, having a mass equal to that of an electron, is ejected from the nucleus. The ejected particles, however, may have either a positive or negative charge and so, although they are known collectively as beta-particles, negative beta-particles ⁽β⁻) or negatrons and positive beta-particles (β⁺) or positrons both exist. Although the negatron is exactly the same as an electron, in this and subsequent chapters the term negatron will be used to describe the particle which exits from the nucleus of an atom while the term electron will be used to describe particles which orbit the nucleus of the atom. Because the processes are different for the production of the negatron and the positron, they will be dealt with under separate headings.

19.5.1 Negatron (β⁻) emission

As we can see from Figure 19.2, β⁻-particles are emitted from nuclei which have too many neutrons for nuclear stability. As we saw in Chapter 18, nucleons are being constantly changed from proton to neutron and back within the atomic nucleus. A neutron may be thought of as consisting of a proton and a negatron:

Equation 19.2

It appears that in nuclei which have too many neutrons, there is a finite possibility that a neutron becomes isolated within the nucleus and then decays to form a proton and a negatron. The proton rejoins the nucleus and the negatron is ejected. This transformation results in the atomic mass number remaining unchanged (the combined number of protons and neutrons is still the same) but the atomic number will increase by one as one extra proton has been added to the nucleus (this results in the formation of a different element with the consequent rearrangement of electron orbitals to suit the new element).

An example of β⁻-particle decay is shown below, where carbon-14 decays to form nitrogen with the emission of a β⁻-particle:

Equation 19.3

This can also be illustrated using the methods discussed for alpha-particle emission to show the transformation from parent to daughter product. Such a diagram is shown in Figure 19.4. Note that this time there is an increase in the atomic number so the line is down and to the right. This simple decay process is an example of pure beta emission since no other transformations are involved.

Figure 19.4 An example of pure beta-particle (negatron) emission. The nucleus increases in atomic number and loses energy as shown.

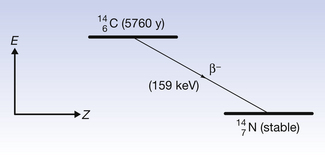
Figure 19.5 shows a more complex emission pattern where the parent and daughter nuclei are separated by an energy difference of 2.81 MeV. The β⁻-particle has an energy of 0.31 MeV and so the nucleus is left in an excited state – 2.50 MeV above its ground state. The nucleus emits this energy in the form of two gamma-rays, one of energy 1.17 MeV and the other of energy 1.33 MeV. (This will be discussed further when we consider gamma-ray emission in Sect. 19.6.)

Figure 19.5 The decay of cobalt-60 as an example of beta decay followed by a gamma decay of the daughter nucleus.

19.5.2 Positron (β⁻) emission

As mentioned earlier, protons are continuously changing into neutrons and back. In these reactions we can consider a proton as consisting of a neutron and a positron.

Equation 19.4

If we consider Figure 19.2, we see that positron emission takes place from nuclei which have too many protons to achieve stability. In such cases, protons appear to become isolated within the nucleus and then to decay to form a neutron which rejoins the nucleus and a positron which is ejected from the nucleus. In this reaction, the atomic mass number will remain the same but the atomic number will decrease by one (the total number of protons and neutrons is unchanged but one proton has been converted into a neutron).

An example of such a reaction is the decay of carbon-11 to boron:

Equation 19.5

If we consider the energy changes which take place within the nucleus, as shown in Figure 19.6, we see that the situation regarding energy of the β⁺-particle is not as simple as it is for the β⁻-particle. The energy difference between the parent and daughter nucleus in this case is 1.99 MeV. An energy loss of 2mc²

Only gold members can continue reading. Log In or Register to continue