Fig. 2.1
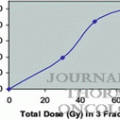
Relative surviving fractions of EMT6 and SCCVII cells after 8 Gy given without a break or in 5 fractions at various intervals. Cell survival after continuous 8-Gy irradiation was regarded as 1. Bars represent SD (Reproduced from Ref. [5] with permission from the publisher)
The effects of 2 Gy given in 5 or 10 fractions at intervals of 0.5–5 min were also investigated in EMT6 cells using the cytokinesis-block micronucleus assay [6]. When the interval was 5 min, 5 fractions of 0.4 Gy corresponded to a single dose of 1.72 Gy. With an interval of 3 min each, 10 fractions of 0.2 Gy corresponded to a single dose of 1.76 Gy. It was concluded that dose-modifying factors of 1.08–1.16 need to be considered when the total irradiation time is 20–30 min. However, further in vivo study was considered necessary to extrapolate this result to clinical situations.
The next in vitro study was conducted to investigate the effects of intermittent irradiation with various fractionation schedules [7]. A total dose of 8 Gy was given to EMT6 and SCCVII cells in 2, 5, 10, 20, and 40 fractions within a fixed period of 15, 30, or 46 min, and the effects were compared with continuous 8-Gy irradiation given at a dose rate of 1.55 Gy/min or at reduced dose rates over 15, 30, or 46 min. When the total radiation time was 15 min, there were no differences in cell survival among the fractionation schedules, but when the period was 30 or 46 min, the radiation effect tended to decrease with an increase in the fraction number up to 20 fractions (Fig. 2.2). Two-fraction irradiation yielded the greatest effect among the fractionated radiation groups. Continuous low-dose-rate irradiation had a greater effect than 20- or 40-fraction irradiation. Implications regarding the clinical application of these results are complicated; nevertheless, this study showed that biological effects could differ with the fractionation schedule even when the total radiation time and dose are identical. To minimize the decrease of biological effects, total irradiation time should be kept as short as possible.
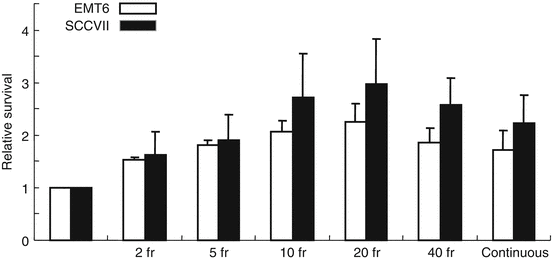

Fig. 2.2
Relative surviving fractions of EMT6 and SCCVII cells after 8 Gy given in 2–40 fractions and prolonged continuous irradiation given over 46 min. The control group received a single dose of 8 Gy over 5.3 min. Cell survival of the control group was regarded as 1. Bars represent SD (Reproduced from Ref. [5] with permission from the publisher. Regarding differences between groups, see Ref. [7])
2.2.2 Effects of Intermittent Irradiation on Murine Tumors and Rapid Reoxygenation In Vivo
Using subcutaneously transplanted EMT6 and SCCVII tumors, the effects of 20 Gy in 2, 5 or 10 fractions delivered at various intervals were investigated [8]. Within 24 h from the first irradiation, the tumors were excised, and tumor cell survival was determined in vitro. Figure 2.3 shows the results of a 5-fraction experiment. Contrary to the in vitro data, no decrease in radiation effects was observed; instead, by placing 2.5-, 7.5-, 10-, or 15-min intervals for EMT6 tumors and 2.5-, 5-, 7.5-, or 15-min intervals for SCCVII tumors, the effect became stronger. Similar results were obtained in 10-fraction experiments. It was speculated that SLDR in vivo might be counterbalanced or overweighed by other phenomena such as reoxygenation.
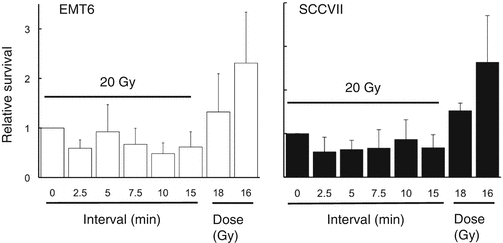

Fig. 2.3
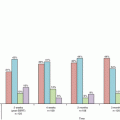
Relative surviving fractions of EMT6 and SCCVII cells irradiated in vivo at 16, 18, or 20 Gy without a break or 20 Gy in 5 fractions at various intervals. Cell survival after continuous 20-Gy irradiation was regarded as 1. Bars represent SD (Reproduced from Ref. [5] with permission from the publisher)
Therefore, reoxygenation at 0–15 min after 13-Gy irradiation in 1-cm-diameter SCCVII tumors was investigated using a paired survival curve assay [9]. As shown in Fig. 2.4, the hypoxic fraction was 100 % at 0 and 2.5 min after the end of the 13-Gy irradiation, but, at 5 min, it fell to 67 % (95 % confidence interval, 41–93 %). Thus, reoxygenation was observed at 5 min after irradiation. It was suggested that rapid reoxygenation could compensate for SLDR in vivo. It should be noted, however, that intermittent radiation decreases the radiation effects in vivo due to SLDR when reoxygenation is restricted. This was shown in a growth delay assay of SCCVII tumors [9].
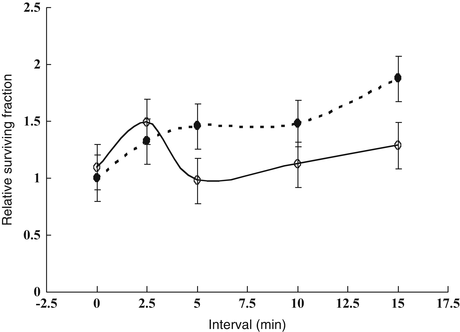

Fig. 2.4
Relative surviving fractions of SCCVII tumor cells after a priming dose of 13 Gy and a second dose of 15 Gy given at 0–15-min intervals to air-breathing (○) or dead (●) mice. The surviving fraction in the dead group that received the second dose immediately after the priming dose was regarded as 1. The hypoxic fraction is given by the surviving fraction of tumor cells in air-breathing mice divided by that in dead mice at respective time points. Bars represent SE (Reproduced from Ref. [5] with permission from the publisher)
2.2.3 Other Laboratory Studies on the Biological Effects of Intermittent Irradiation
In classic studies by Elkind et al. [1, 2], a significant increase in cell survival due to SLDR was observed when intervals of 30 min or longer were set between two radiation doses. However, they never investigated shorter intervals. After the 1990s, Benedict et al. [10] attempted to estimate dose-correction factors for stereotactic radiosurgery using U-87MG cells in vitro. In their experiments, the effect of radiation decreased with prolongation of the treatment time, and the correction factor of 0.02–0.03 Gy/min was proposed when a total dose of 6–18 Gy was given. This indicates that when the treatment time prolongs by 30 min, 8 Gy would correspond to approximately 7.1–7.4 Gy delivered continuously, giving dose-modifying factors of 1.08–1.13. These results agree with our own.
Moiseenko et al. [11] investigated the correlation between the magnitude of the loss of effect brought about by prolonged radiation delivery and the α/β ratio in three cell lines. When their results were projected to a 30-fraction treatment, the dose deficit to bring cell survival to the same level was 4.1 Gy in one line, but it was as large as 24.9 and 31.1 Gy in the other two lines. The dose deficit did not relate to the α/β ratio of the three cell lines. On the other hand, Zheng et al. [12] also investigated the issue in two hepatocellular carcinoma cell lines, and a significant decrease in cell survival due to prolonged fraction delivery was observed in one line with an α/β ratio of 3.1 Gy but not in another with an α/β ratio of 7.4 Gy. Therefore, the relationship with the α/β ratio remains unclear and requires further investigation.
All these results indicate that SLDR takes place when radiation delivery is prolonged or given intermittently in daily stereotactic irradiation settings. However, it should be noted that these results were obtained using cultured single cells. Until recently, there have been no in vivo studies except for our own ones, but other studies have been published. The results of a study by Wang et al. [13] agree with our own; when C57BL mice bearing Lewis lung cancer were irradiated under conditions of limited reoxygenation, intermittent radiation delivery led to a significant reduction in the biological effects. The study by Jiang et al. [14] also showed a similar result. However, more in vivo investigations appear to be warranted in the near future. Our study suggests that SLDR in vivo can be counterbalanced by reoxygenation. In tumors that reoxygenate rapidly, the adverse effects of prolonging the radiation delivery time may be none or negligible. However, little is known about the reoxygenation in human tumors, so this issue is also an important topic to be investigated in the future to elucidate the effect of intermittent or prolonged radiation delivery in clinical practice.
2.3 Applicability of the LQ Model to High-Dose-per-Fraction Radiotherapy
2.3.1 Current Controversy
To compare different fractionation schedules, the LQ formalism (n2d2/n1d1 = (1 + d1/[α/β])/(1 + d2/[α/β]), where d1 and d2 are fractional doses and n1 and n2 are fraction numbers) and the biologically effective dose (BED) derived from the LQ model (BED = D(1 + d/[α/β]), where D is the total dose and d is the fractional dose) are often used because of their convenience and simplicity [4, 15]. While LQ formalism is useful for conversion between relatively low radiation doses as used in conventional radiotherapy, it has been suggested that it is not applicable to higher daily doses or smaller fraction numbers [4, 5]. However, many clinicians have used LQ formalism to convert hypofractionated doses to single doses in their publications [16, 17], and many have used BED to evaluate the doses of stereotactic irradiation [18, 19]. To further complicate the issue, some investigators claim that the LQ model is applicable to stereotactic irradiation [20, 21]. The ground for the latter group is somewhat limited in that the existing clinical data do not significantly deviate from those expected from LQ model calculations, and their data do not necessarily indicate that the LQ model fits best to the high-dose data. Since clinical data usually contain large errors, experimental evaluation of the reliability of the LQ model in single-fraction and hypofractionated radiation schedules appears to be important.
2.3.2 Cell Survival Data for the Reliability of the LQ Model at High Doses per Fraction
The theoretical basis behind the LQ model not being applicable with high doses per fraction is that dose-survival curves for cultured cells cannot be fitted well by the LQ model in high-dose ranges. This has been pointed out for a long time; in the pioneering work of Puck and Markus [22] who established the colony formation assay, the high-dose region of the dose-survival curve was apparently straight in HeLa cells. Therefore, the LQ model, with which the cell survival curve continues to bend downwards at high doses, does not seem to fit the actual curves at high doses. Joiner and Bentzen [4] stated that extrapolation by the LQ model beyond 5–6 Gy per fraction is likely to lack clinically useful precision. More recently, Garcia et al. [23] investigated the compatibility of the LQ model regarding dose-survival curves of 4 cell lines in broad dose ranges. In the 4 lines, the LQ model did not fit the curves at high dose ranges that were >7.5–13 Gy depending on the cell line. Therefore, the inadequacy of the LQ model at high doses was demonstrated.
Our group investigated the reliability of LQ formalism in converting hypofractionated doses (in 2–5 fractions) to single doses in cultured cells and spheroids [24]. The study showed that LQ formalism is inadequate in doing so; the equivalent single doses for the hypofractionated doses calculated by LQ formalism were apparently lower than the equivalent single doses actually measured. LQ formalism underestimated the effect of fractionated irradiation. The magnitudes of errors were 6–19 % for 2- or 3-fraction schedules in V79 and EMT6 single cells, and 18–30 % for 2- to 5-fraction schedules in V79 spheroids. In a more recent study [25], we investigated the applicability of the BED in EMT6 cells. The α/β ratio of the cells determined from single-dose experiments was 3.18 Gy, and a BED3.18 for 20 Gy in 10 fractions was calculated to be 32.6 Gy. Fractional doses yielding the same BED3.18 were calculated for 1-, 2-, 3-, 4-, 5-, 7-, 15- and 20-fraction irradiation using LQ formalism, and then irradiation with these schedules was actually given. The effects of 7-, 15- and 20-fraction irradiation with a BED3.18 of 32.6 Gy were similar to those of the 10-fraction irradiation, while the effects of 1- to 5-fraction irradiation were lower (Fig. 2.5). In this cell line, the LQ model was considered applicable to 7- to 20-fraction irradiation or doses per fraction of 2.57 Gy or smaller.
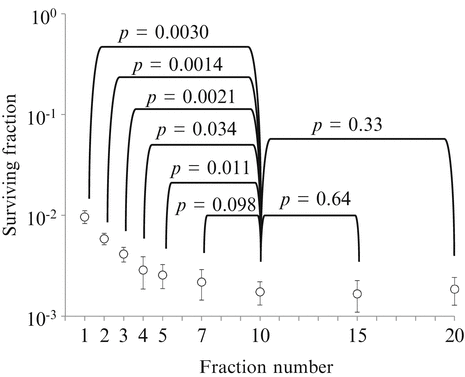

Fig. 2.5
Surviving fractions of EMT6 single cells after single or fractionated irradiation with a BED of 32.6 Gy for an α/β ratio of 3.18 Gy. Bars represent standard deviation. If the BED concept is correct, cell survival should be at the same level, irrespective of the fraction number (Reproduced from Ref. [25] with permission from the publisher)
Since the reoxygenation of hypoxic tumor cells is considered to have a great influence on the compatibility of the LQ model [9, 26], the applicability of LQ formalism for converting hypofractionated doses (in 2–5 fractions) to single doses was evaluated using murine EMT6 tumors [27]. Again, the use of LQ formalism produced large errors; the equivalent single doses for the hypofractionated doses calculated from LQ formalism were much lower than the equivalent single doses actually measured. The magnitudes of errors were larger than those seen in the in vitro study; they were 21–31 % for 2- or 3-fraction schedules and 27–42 % for 4- or 5-fraction schedules. The possible larger discrepancy in in vivo tumors as compared to in vitro single cells and spheroids was considered to be largely due to the reoxygenation during interfraction intervals in the hypofractionated groups. This study clearly showed that LQ formalism is inadequate for high-dose-per-fraction radiotherapy, especially in in vivo tumors.
To further evaluate the appropriateness of the BED concept in hypofractionated irradiation, we compared 2- to 5-fraction irradiation schedules simultaneously in the EMT6 tumors in Balb/mice [27]. Total doses of 18–30 Gy were given in 2–5 fractions to the tumor-bearing mice at 4-h intervals, and tumor cell survival was assessed with an in vivo–in vitro assay. Cell surviving fractions were plotted against the total dose and BED3.5. In the in vitro cell survival determination conducted along with the in vivo experiment, the α/β ratio of the cell line was 3.5 Gy, so BED3.5 was adopted as a substitute for “BED10” often used clinically to represent the tumor response. As shown in Fig. 2.6, respective dose-response curves almost overlapped when cell survival was plotted against actual radiation doses. However, the curves tended to shift downwards by increasing the fraction number when cell survival was plotted against BED3.5. If the BED concept is correct, the respective cell survival curves would overlap on this figure. Thus, it seems that BED is inadequate for use in SBRT, especially for tumors. The total dose reflected the actual effect (tumor cell survival) more accurately than BED in this experiment. The calculated BED tended to become larger than expected from the actual effects when the fraction number decreased. Thus, BED tends to overestimate the actual effects with increasing radiation doses.
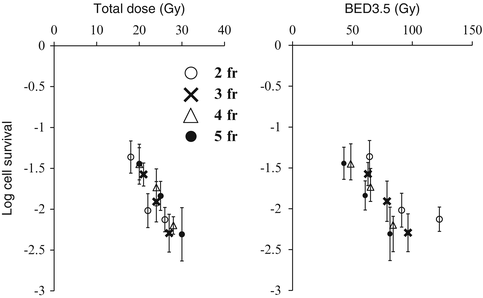

Fig. 2.6
Surviving fractions of EMT6 cells in vivo after 2-fraction (○), 3-fraction (X), 4-fraction (△), or 5-fraction (●) irradiation plotted against the total radiation dose and BED3.5. Bars represent SE (Reproduced from Ref. [5] with permission from the publisher)
2.3.3 Normal Tissue Response Data for the Reliability of the LQ Model at High Doses per Fraction
The reliability of the LQ model can also be evaluated based on normal tissue data. In classic radiobiology studies, raw data for various normal tissue responses from animal and human studies were presented as a series of dose-response curves [28–31]. Measured responses were plotted against total radiation doses for each schedule. From horizontal cuts, isoeffect doses could be read off, and these isoeffect doses could then be plotted as a log dose against the log number of fractions or log fraction size. Since the isoeffect curves are concave downwards, it is difficult to determine any particular slope for the curves. Instead, the isoeffect curves can be plotted as the reciprocal total dose as a function of the dose per fraction [31]. This reciprocal total dose or Fe plot was elaborated to estimate the α/β ratio of normal tissues [28]. When the normal tissue response data fall in a straight line on this Fe plot, the LQ model is considered to be appropriate. The isoeffect curves for most normal tissues were linear in the dose range of 1–8 Gy [32], suggesting that the LQ model is adequate in this range of dose per fraction. Brenner [21] found that the isoeffect curves for the rat spinal cord response, mouse skin reaction, and murine intestinal damage could be visually fitted with straight lines in the dose range between 0 and 25 Gy, and insisted that the LQ model is applicable throughout this dose range. However, statistical validation of the linearity was not performed. Later, Astrahan [33] analyzed the data for various normal tissues in more detail, and found that the LQ formula closely fitted the curve for the late reaction of the mouse spinal cord for fractions up to about 10 Gy. However, the data for cervical vascular damage did not fit the LQ model but fitted the linear-quadratic-linear (LQL) model, which is stated later. Fowler et al. [34] suggested that for certain epithelial tissues, the LQ model may be applicable up to 23 Gy per fraction.
These observations are somewhat contradictory and confusing, but the discrepancy may be, in part, explained by the α/β ratio for the normal tissue responses. The applicability of the LQ model may not simply depend on the absolute dose per fraction; for a tissue with a large α/β ratio, its applicability may be extended to a higher dose region. This is the case with epithelial tissues that usually have an α/β ratio of around 10 Gy. Since the α/β ratio represents the dose at which cell killing from linear (α) and quadratic (β) components of the LQ formula is equal, the LQ model holds around the dose level of the α/β ratio. However, with the increase in the dose, the β cell kill component dominates in the LQ model, from which actual cell-survival data have been shown to deviate. This deviation appears to become evident in the dose range over two-fold the α/β ratio [23]. From these considerations, it may be said that the model is applicable up to a radiation dose approximately two-fold the α/β ratio.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree