In general, all high-LET emitters are much more effective for small lesions and for micrometastatic disease. For example, with a decrease in tumor size from 1 to 0.2 mm, the alpha emitter At-211 (energy transfer ~80 keV/mm) is 9–33 times more effective than the low LET (~1 keV/mm) Y-90. At the cell surface, At-211 is 1,200 times more effective than the high-energy beta emitter Y-90 (Srivastava 1996a, b, c). Because of their shorter range, and since there is none or insignificant crossfire, high-LET emitters may be less effective for large tumor masses and macrometastatic disease, even though the distribution within the lesion may be homogeneous. High-LET radiopharmaceuticals require a higher degree of selectivity of localization and this requires better and more specific targeting mechanisms. Ultimately, the selection of an appropriate particle emitter depends upon the nature, the extent, and stage of disease. Conversion electrons by definition are associated with internal conversion which is an isoenergetic radiationless transition between two electronic states. Certain low-energy conversion electron emitters, for example tin-117m, offer an almost ideal combination of properties (Srivastava 2012). Tin-117m emits an imageable gamma photon in good abundance and short-range conversion electrons with a high linear energy transfer, and a high S value, which results in high quality therapeutic radiation. These properties can translate into a very high localized dose to diseased tissue with minimal toxicity to normal organs or non-target tissues, as long as the targeting is very specific. Commonly used beta emitters in comparison have much lower linear energy transfer and the emitted electrons resemble a plume that travels over a longer distance which translates into less intense localized therapeutic effect. However, they are often better suited for treating bigger lesions or macro-metastatic disease due to the cross-fire effect (Srivastava 2006).
1.3 Selection Criteria for Therapeutic Radionuclides
The selection criteria must be based on the physical data about the radionuclide, its production and chemistry, and biological variables governing its use. The important physical variables to consider include the radionuclide half-life, the type, energy, and branching ratio of particulate radiation and the gamma-ray energies and abundances. It is important to match the physical half-life with the in vivo pharmacokinetics of the carrier molecule used for targeting. If the half-life is too short, most decay will have occurred before the radiolabeled targeting molecule (radioconjugate) has reached the maximum tumor-to-background ratio.
Conversely, considerations of tumor radiobiology and low radioconjugate-specific activity concentration may also limit the use of long-lived radionuclides. For equal radioactivity concentrations in the target, radionuclides with long half-lives will produce a lower absorbed dose rate than those with short lifetimes. If the maximum absorbed dose rate from beta particles is much lower than that typical in brachytherapy (40–60 cGy/h), cell kill per cGy will be decreased (Fowler 1991; Dale 1985).The theoretical low specific activity of longer lived radionuclides would thus require a large mass of radionuclide, ligand, and the carrier molecule to achieve adequate dose rate. This can make the use of long-lived radiolabels less desirable. However, if a two- or three-stage therapy approach is utilized (Britton et al. 1991), it becomes useful to consider the use of long-lived beta emitters, e.g., P-32 and others. To some extent, the problem of low target dose rate may be counteracted by a number of factors including high non-penetrating equilibrium dose constant, high target to nontarget ratio, high carrier labeling efficiency, and the ability to administer a large carrier molecule mass (tumor saturation effect).
The type of particulate emission also must be considered. The potent lethality of Auger and low-energy conversion electrons has been demonstrated (Bradley et al. 1975; Chan et al. 1976; Kassis et al. 1982; Adelstein and Kassis 1987; Feinendegen 1975). As mentioned earlier (Srivastava 1996a, b, c, 2012), this effect can best be realized with intranuclear localization of the radionuclide, which does not generally occur with many radioconjugates, in particular peptides and monoclonal antibodies (Srivastava 1988). Of course, α particles have a high LET effective in cell killing and a range of several cell diameters, 40–80 μm. The short ranges will accentuate inhomogeneous absorbed dose particularly when the radioconjugate deposition is inhomogeneous. Beta particles are less densely ionizing and have a range longer than α’s so that the distribution requirements are less restrictive for treatment (e.g., radioimmunotherapy, RIT) of bulky disease. On the other hand, for disseminated metastatic disease or micrometastases, the absorbed fraction for higher energy beta particles (range > tumor size) is decreased, leading to a less favorable tumor absorbed dose. The gamma-ray energies and abundances are also important physical properties, because the presence of gamma rays offers the possibility of external imaging for biodistribution and dosimetry. These physical properties alone can be used to calculate radiation absorbed dose at the cellular level. This approach has been used by Jungerman et al. (Jungerman et al. 1984) to estimate delivered doses for RIT. An approach which explicitly includes biodistribution and kinetic data by using an idealized time-dependent averaged target-to-nontarget uptake ratio is that of Wessels and Rogus (Wessels and Rogus 1984). Although the quantitative dose ratios are highly dependent on the input biodistribution data, a comparison of the relative effectiveness of the radiolabels was demonstrated. This relative efficacy was approximately constant for reasonable variation of model parameters in accordance with observed biological data. A similar approach was also used by Yorke et al. (Yorke et al. 1991). Also, Humm (Humm 1986) has considered the effect on monoclonal antibody (MAb) dosimetry of varying tumor size and of cold regions. These papers underscore the importance for therapy of a high ratio of non-penetrating to penetrating (γ) radiations. The complex relationship between tumor curability with different radionuclides and tumor size has been reviewed by Wheldon and O’Donoghue (Wheldon and O’Donoghue 1990).
The main chemical variables to be considered in choosing a radionuclide for therapy with carrier molecules, in particular MAbs and other proteins, and peptides, are the radionuclide-specific activity achievable, metal-ion contamination, the number of labels per MAb molecule obtainable without loss of immunological activity, and the stability of the radionuclide-protein attachment. The specific activity, or amount of activity per mass of the element in question (MBq/mg), depends primarily on the method of production. Simple neutron absorption reactions (e.g., n, γ) generally give low specific activity since the radionuclide cannot be chemically separated from a target of the same element. Accelerator-based proton, deuteron, or alpha-induced reactions are intrinsically no-carrier-added (NCA) methods that do allow chemical separation of product from the target. This can also be achieved at reactors by neutron absorption reactions leading to an intermediate product with beta decay to the desired final product, or by fast neutron reactions such as (n, p). The achievable specific activity of these NCA methods then largely depends on the impurity levels of the product element in the target or in various reagents used in processing. An often overlooked source of carrier is due to the direct production of stable isotopes of the product element. Although this effect is often negligible compared to carrier introduced with the target, it can become significant with very pure targets and high bombarding energies. With increasing energy, the typical peaks in nuclear excitation functions broaden, usually reaching a plateau at approximately 150–200 MeV, and reaction cross sections for neighboring isotopes become comparable over large energy ranges. Some of these issues have been reviewed for therapeutic radionuclides (Volkert et al. 1991, ).
The presence of metal ions other than the product is a concern as they can compete for binding sites on bioconjugates. It is largely controlled by the selectivity of the chemical separation scheme, but this process is not perfect. For example, a normally adequate separation factor of l0−7 on a 10 g target still leaves 1 μg of target in the product which may be of concern when labeling at low protein concentrations. Indeed, measurement of these stable species at low concentration in radioactive solutions is often a very difficult practical problem. Although various analytical procedures exist for detecting ions at less than part per million levels, for example atomic absorption, emission spectroscopy, mass spectroscopy, and X-ray fluorescence, etc., these techniques often take time, utilize expensive instrumentation, and may require a large fraction of the final product solution for the measurement. Generally, the sooner the radionuclide is used the better, because its specific activity is highest, and this need competes with the desire to measure the specific activity and impurity levels. Also, it is typical for many research groups that the expensive analytical apparatus is not wholly owned. Instead, access is through a shared use facility whose operators are very reluctant to introduce radioactive material into their equipment. Thus the fastest, albeit indirect method, of determining carrier levels may simply be by titration with the bioconjugate chelate during labeling.
The convenience, efficiency, and gentleness of various radiolabeling procedures as well as the stability of the radionuclide attachment to the antibody are all very important factors which are being actively investigated by many groups. They will not be considered further here as these topics are beyond the scope of this chapter and will be discussed elsewhere in this volume, and have also been reviewed previously (Fritzberg et al. 1988; Hnatowich 1990; Gansow 1991; Srivastava and Mease 1991). While recognizing the difficulties in designing new conjugation (labeling) schemes, at this point it is simply assumed that adequate radiolabeling techniques either exist or will become available for use with radionuclides to be discussed (Gansow 1991; Srivastava and Mease 1991). However, another practical aspect to be considered is that of radionuclide production—the routine availability, at reasonable cost, of quantities of radioactivity suitable for therapy. At present, very few therapeutic radionuclides truly meet all of these production criteria. However, this situation is changing for several other attractive radionuclides to be discussed in this chapter.
These physical and chemical factors must then be viewed in light of available biological information. For example, in the case of MAbs, there is substantial variation in uptake, macro- and micro-distribution, kinetics, and processing (metabolism/catabolism) depending on the particular antibody, antibody dose, the variability of antigenic expression in the tumor, its size and stage, etc. Limitations due to normal tissue radiotoxicity are not entirely the function of radionuclide emissions but are largely governed by the pharmacokinetics of the antibody. For many of the MAbs and MAb fragments currently being investigated for immunotherapy some generalities do emerge. It is generally believed that one-half to 3 days is usually required to reach maximum tumor uptake (DeNardo et al. 1982, 1988; Larson et al. 1988; Scheinberg and Strand 1983) although optimum contrast with whole MAbs may take longer. Despite the presence of numerous antigen sites on cancer cells, evidence from tumor implanted microthermoluminescent dosimeter probes (Wessels et al. 1985; Griffith et al. 1988) and autoradiography (Buchegger et al. 1988) indicates a non-uniform cellular distribution of the MAb in most cases. This may be due to cell-type heterogeneity (Buick et al. 1983), heterogeneity of antigenic expression (Fabre and Daar 1983), poor delivery, and spatial inaccessibility. These factors considerably reduce the attractiveness of short-ranged alpha-emitting radionuclides for radioimmunotherapy. A role for alpha emitters may be feasible in specific cases such as for micrometastases or intracavitary administration for some types of cancers, such as peritoneal injection for ovarian carcinoma (Bigler and Zanzanico 1988; Wilbur 1990). The longer range of beta particles can still permit uniform tumor irradiation despite a marked heterogeneity of distribution of radioactivity within the tumor. It appears desirable to deliver ionizing radiation with a range of one to several millimeters in tissue, as from intermediate to high-energy beta particles.
A list of current as well as future therapeutic radionuclides, chosen arbitrarily on the basis of particle emission and a few other parameters, is presented in Table 1. The nature of the delivery vehicle depends upon the mechanisms that could be used to selectively target lethal doses of the radionuclide to the diseased tissue. A few representative examples of the approaches for cancer therapy using suitable radionuclides are shown schematically in Fig. 2.
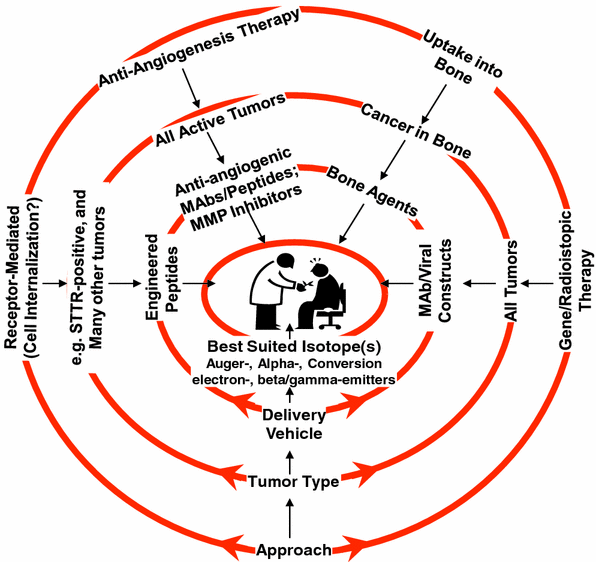
Table 1
Present and future therapeutic radionuclides
Nuclide | T ½ | Particle emissiona | Eavg, keVb (% per decay) | Principal gamma component E, keV(%) |
|---|---|---|---|---|
P-32c | 14.3 days | β− | 695 | – |
Sc-47 | 3.3 days | β− | 162 | 159 (68) |
Cu-67 | 2.6 days | β− | 141 | 185 (49) |
Ga-67 | 3.3 days | Aug | 0.04–9.54 (572) | 93 (37) |
As-77 | 1.6 days | β− | 228 | 239 (1.6) |
Sr-89c | 50.5 days | β− | 583 | – |
Y-90c | 2.7 days | β− | 935 | – |
Rh-105 | 1.5 days | β− | 190 | 319 (19) |
Pd-109 | 0.6 days | β− | 360 | 88 (4) |
Ag-111 | 7.5 days | β− | 350 | 342 (7) |
In-111 | 2.8 days | Aug | 0.5−25 (308) | 171 (90); 245 (94) |
Sn-117m | 14.0 days | C.E. | 127−152d | 159 (86) |
I-123 | 13.2 h | Aug | 0.7–30 (289) | 159 (83) |
I-125 | 60.1 days | Aug | 0.7–30 (479) | 36 (7) |
I-131 | 8.0 days | β− | 181 | 364 (81) |
Sm-153 | 1.9 days | β− | 225 | 103 (28) |
Gd-159 | 0.8 days | β− | 311 | 363 (8) |
Dy-165 | 2.33 h | β− | 438 | 95 (4) |
Ho-166 | 1.1 days | β− | 666 | 80 (6) |
Er-169c | 9.3 days | β− | 111 | – |
Lu-177 | 6.7 days | β− | 140 | 208 (11) |
Re-186 | 3.7 days | β− | 329 | 137 10) |
Re-188 | 0.7 days | β− | 795 | 155 (15) |
Ir-194 | 0.8 days | β− | 808 | 328 (13) |
Hg-195 m | 1.7 days | C.E. | 13–259 (180) | 262 (32) |
Aug | 2.5–9.6 (409) | |||
Pt-195 m | 4.0 days | C.E. | 17–130 (276) | 99 (11) |
Aug | 2.4–63 (466) | |||
Au-198 | 2.7 days | β− | 311 | 412 (95) |
Au-199 | 3.1 days | β− | 143 | 158 (37) |
Tl-201 | 3.0 days | Aug | 2.7–77 (253) | 167 (11) |
At-211 | 7.2 h | α | 5868 (41) | 79 (21.3) |
Bi-212 | 61 min | α | 6051 (25) | 727 (7) |
α | 2246 (max) | |||
Bi-213 | 46 min | α | 1390 (max) | 440 (26) |
α | 5870 | |||
Ra-223 | 11.43 days | α | 5979 | several gammas |
12–351 | ||||
81–95 (52) | ||||
Ac-225 | 10.0 days | α | 5915e | 99(93) |
Fm-255 | 0.8 days | α | 7030 (93) | 109 (24.6) |
Fig. 2
Schematic representation of the central role of radionuclides for certain promising approaches for therapy of cancer
1.4 Theragnostic Radionuclides
As mentioned in the text earlier, radionuclides have a major advantage in that that they emit radiation of different radiobiological effectiveness and range of action, which offers the possibility of choosing a nuclide the physical and nuclear characteristics of which are matched with a particular tumor type, or the disease under treatment. Also, certain radionuclides or radionuclide pairs have emissions that allow pre-therapy information with low-dose imaging, followed by higher dose therapy in the same patient (Srivastava 2009, 2010, 2011, 2012). Such dual-purpose theragnostic radionuclides, for example I-131, or the pair I-124/I-131 have been around and used for imaging followed by therapy, without consideration of the fact that the optimum radionuclide or the optimum radionuclide pair was not scientifically or methodically chosen with this requirement and/or with the particular disease in mind. Over two decades ago, when Y-90 began to be promoted for radioimmunotherapy and was undergoing rapid development, it was considered necessary to use In-111-MAb as a surrogate to carry out biodistribution and imaging studies in order to predict the dosimetry and toxicity prior to doing the therapy with Y-90-MAb, because of the lack of imageable photons in Y-90 emissions. After some very careful studies, the Julich group (Herzog et al. 1993) and our own group at Brookhaven (Srivastava 1988; Srivastava and Dadachova 2001) showed that at best, it was hazardous to do so because these were two different elements whose biochemistry had many similarities but also many striking dissimilarities as well. Interestingly, this practice still continues, because of the lack of an alternate solution (Traub-Weidinger et al. 2011). In such a situation, it would have been best to use the positron emitter Y-86, a congener of Y-90, and therefore with the same chemical and biochemical properties, to carry out pre-therapy PET imaging, so that imaging predicts biodistribution and dosimetry in a reliable, individualized fashion, and thus also predicts which patients will respond to the radionuclide therapy with Y-90 and which will not. However, Y-86 until very recently has not been available at all or only in insufficient quantities for this purpose. This situation is now changing and in many cases, if the therapeutic isotope has no photon emission, suitable congeners for imaging are becoming more and more available.
It is noteworthy that a number of such radionuclides or radionuclide pairs do exist (Srivastava 2009, 2010, 2011, 2012) and it would make a lot of sense to direct their use for the development of “theragnostic radiopharmaceuticals”. It is important to stress that ideally, for theragnostic use, the molecularly targeted radiopharmaceutical should constitute the same dual-purpose radionuclide with both imaging and therapeutic emissions. In the second best situation, as mentioned above for the Y-90 situation, a radionuclide pair (imaging photon emitter, either gamma or positron, and a congener of the therapeutic particle emitter, with the same electronic structure) can be used as well. One caveat here, which is a fact of life, is that even though many theragnostic PET/therapy radionuclide pairs may have the same electronic structure, their production and processing methodologies may be significantly different leading to the fact that their chemistry and in vivo behavior may be different as well due to differences in chemical species, charge, specific activity, etc., and/or the amount of chemical and radionuclidic and chemical impurities, which cannot be totally removed. Another caveat that one has to deal with is the issue of half-life of the imaging PET congener which in most cases might be much shorter than the usually (desirable) longer half-life of the therapeutic congener. In most situations, the determination of longer term biodistribution and dosimetry would be crucial but this information would not be achievable using the shorter-lived PET congener for pre-therapy imaging.
The theragnostic radionuclides or radionuclide pairs would initially allow molecular imaging (SPECT/CT or PET/CT) to provide the required and useful pre-therapy information on biodistribution, dosimetry, the limiting or critical organ or tissue, and the maximum tolerated dose (MTD). If the imaging results then warrant it, it would be safe and appropriate to follow-up with dose ranging experiments to allow higher dose targeted molecular therapy with the greatest effectiveness. These factors are especially important in order to be able to do tailored imaging plus therapy (personalized medicine) in the same patient with the same radiopharmaceutical (Srivastava 2009, 2010, 2011, 2012).
The discussion in this chapter that follows deals both with single theragnostic radionuclides, as well as the PET/therapy theragnostic radionuclide pairs. In addition, a few other promising therapeutic radionuclides that have been under investigation and have become available commercially in sufficient quantities for clinical trials are included. There are indeed a number of individual radionuclides that emit both imaging photons and therapeutic electrons and which would be potentially excellent choices for theragnostic applications (Table 2). Some of the most promising PET/Therapy radionuclide pairs are shown in Table 3. The lists included in both Tables 2 and 3 are not all-inclusive but consist of selected radionuclides and radionuclide pairs that are or could be made available in sufficient quantities to be of practical value, and which show the required combination of nuclear, physical, and chemical properties, and thus the greatest promise. Some other criteria for inclusion were arbitrarily set at a minimum of 20 % photon/positron emission for imaging, and a sufficiently abundant therapeutic particle emission consisting of medium (β−) to high LET electrons. It should be noted that there may be other suitable candidates from the class of alpha and Auger electron emitters (Srivastava 1996a, b, c, 2006, 2012; Kassis et al. 1982; Adelstein and Kassis 1987; Feinendegen 1975), but these have not been included in this theragnostic group of radionuclides (except Ac-225/Bi-213) since their availability is either limited or not enough pre-clinical and clinical experimental data have thus far been available.
Table 2
Selected theragnostic radionuclides
Radionuclide | T 1/2 (days) | Principal y energy for imaging, KeV(%) | Therapeutic particle(s) (avg. energy, KeV, % abundance |
Scandium-47 | 3.35 | 159 (68) | β- (162) |
Copper-67 | 2.58 | 186 (40 | β- (141) |
Gallium-67 | 3.26 | 93. 184, 296 (40, 24, 22) | 15 Auger, 0.04–9.5 keV, 572 % 10 C.E, 82–291 keV, 30 % |
Indium-111 | 2.80 | 171, 245 (91, 94) | 6 Auger, 0.13–25.6 keV, 407 % 12 C.E, 144–245 keV, 21 % |
Tin-117m | 14.00 | 159 (86) | 8 C.E. (141 keV avg., 114 %) |
Iodine-123 | 13.3 h | 159 (83) | 12 Auger, 23–30.4 keV,1371 % 7 C.E, 0.014–32 keV, 17 % |
Iodine-131 | 8.0 | 365 (82) | β- (181) |
Samarium-153 | 1.94 | 103 (30) | β- (280) |
Astatine-211 | 7.2 h | 79 (21) | α (5867, 42 %) |
Bismuth-213 | 46 min | 441 926) | β- (425); α (98 %, from Tl-209 daughter, 2 % from Bi-213) |
Table 3
Selected theragnostic radionuclide pairs
Radionuclide pair imaging/therapeutic | T 1/2 (days) | Imaging positron, KeV (%) | Therapeutic particle(s) (avg. energy, KeV) |
|---|---|---|---|
Scandium-44/Scandium-47 | 3.97/3.35 | y ± 511 (99.9%) | β- (162) |
Copper-64/Copper-67 | 0.53/2.6 | y ± 511 (38%) | β- (141) |
Gallium-68/Gallium-67 | 68 min/3.26 | y ± 511 (176%) | 15 Auger, 0.04–9.5 keV, 572 % 10 C.E., 82–291 keV, 30 % |
Yttrium-86/Yttrium-90 | 0.61/2.7 | y ± 511 (35%) | β- (935) |
Iodine-124/Iodine-131 | 4.2/8.0 | y ± 511 (38%) | β- (181) |
1.5 Availability Issues
A major problem that remains yet to be completely resolved is the lack of availability of a number of the best candidate therapeutic radionuclides, in particular the theragnostic radionuclides or PET/SPECT radionuclide pairs, in sufficient quantities and/or in a no-carrier-added (NCA) form. Methods have already been studied and developed for the production of research quantities of certain theragnostic radionuclides and radionuclide pairs listed in Tables 2 and 3 in particular Cu-64 (Szelecsenyi et al. 1993), Y-86 (Srivastava 2009, 2010, 2011, 2012; Sadeghi et al. 2009; Medvedev et al. 2011), I-124 (Aslam et al. 2001), and Sc-44 (Huclier-Markai et al. 2011). Gallium-67, Y-90, In-111, I-123, Sm-153, Lu-177, and I-131 are routinely available from commercial sources. Close to sufficient quantities of Ge-68 (parent of Ga-68) are made available mainly from the Brookhaven Linac Isotope Producer (BLIP) at Brookhaven National Laboratory (BNL) (Meinken et al. 2005) and from the Isotope Production Facility (IPF) at Los Alamos National Laboratory (LANL).
A summary description relating to the development of new or modified methods for the production of selected promising theragnostic radionuclides (Sc-47, Cu-67, Y-86, Sn-117m, and Ac-225/Bi-213), as well as a number of other therapeutic radionuclides that have recently become available in reasonable quantities and/or have undergone through various stages of clinical trials, is included in the following sections.
2 Radionuclide Production
Basically, radionuclides can be classified into two main groups, those that are neutron-rich and those that are neutron-deficient. Although this classification is not completely accurate, for the purposes of this chapter, it serves to separate the radionuclides which are usually made in a reactor from those that are made using a particle accelerator. Those that are neutron-rich are usually made in a nuclear reactor while those that are neutron-deficient (or in most cases, NCA) are produced by bombarding a suitable target with protons, deuterons, or helium particles.
Particle accelerators and especially cyclotrons have been very important in the preparation of radioisotopes during the 1930s until World War Two (WWII). The amount of radioactive material that could be produced in an accelerator was several times greater than the amount which could be produced using the alpha particles from naturally occurring radioactive elements. After WWII, reactors began to be used to produce radioactive elements and the use of accelerators for this purpose became less common. However, as the techniques for using radiotracers became more sophisticated, it became clear that reactor produced radionuclides could not satisfy the growing demands and therefore, accelerators were considered preferable and needed to produce new radionuclides which could be used in additional new ways.
As mentioned earlier, among all the therapeutic (or imaging for that matter) radionuclides that have ever been produced, or those that continue to be investigated for production, only a very few have or will end up with the required combination of favorable nuclear, physical, and biological characteristics to become useful for routine clinical use.
2.1 Nuclear Reactions
Many processes can occur when nuclear particles strike a target. Generally, charged particles first collide with atomic electrons producing ionization and excitation of these atoms. Energy is transferred to these electrons thus decreasing the energy of the incident charged particle. The electron energy is ultimately converted into heat. This process can be visualized as the particle plowing through a sea of electrons and dissipating its energy through friction. Neutrons carry no charge, and their interaction with electrons is negligible.
Although relatively infrequent compared to electron interactions, sometimes the incident particle comes close enough to the very small atomic nucleus to transfer some kinetic energy to the nucleus as a whole. The nucleus moves but has no internal excitation. This process is called nuclear elastic scattering and may be visualized as billiard balls colliding. The energy of nuclear motion also eventually dissipates as heat. If the collision involves a close approach of projectile to target nucleus, the particle will be affected by short-range nuclear forces as well as by the Coulomb forces. In this case the direction of the particle changes and it loses kinetic energy to the nucleus, which may become internally excited. Kinetic energy is not conserved in this process which is called nuclear inelastic scattering. The nucleus de-excites very quickly by the emission of one or more gamma rays.
Finally, a particle may be absorbed by the target nucleus that is then excited by the transfer of kinetic energy and the released binding energy of the incident particle. This incident particle is captured and a new heavier nucleus is formed, at least briefly. The highly excited intermediate nucleus can nearly instantaneously de-excite in several ways. It can emit electromagnetic radiation in the form of gamma rays. These gamma rays are called “prompt” to distinguish this mechanism from gamma emission following radioactive decay. If the incident particle is a neutron, this process is called radiative capture. If the nuclear excitation energy is concentrated on a few nucleons (i.e. neutrons and protons), either by direct collision with the incident particle or by statistical processes, nucleons can be ejected. If the total excitation energy of the intermediate state is greater than the binding energy of nucleons within the nucleus, nucleon emission is favored. If not, simple prompt gamma emission returns the new nucleus to a more stable state. This process of conversion of the original nucleus into a new one is a nuclear reaction, and the residual nucleus is the reaction product. This process in which the reaction product is radioactive is of major interest to nuclear medicine.
In the case of neutron bombardment (e.g., in a reactor), there is no Coulomb repulsion from the positively charged nucleus, and neutrons easily penetrate the nucleus. Actually, very low energy neutrons have very large reaction probabilities, and are thus particularly useful for radionuclide production. These neutrons are called “thermal neutrons”, because they have an energy distribution of that of ordinary gas molecules in thermal equilibrium at room temperature. The most probable energy is 0.025 electron volts (eV). Neutrons with energies up to about several keV are often called “epithermal” or “resonance” neutrons, and higher energy neutrons are simply referred to as “fast neutrons”.
Nuclear reactions are written in equation form in analogy to chemical reactions, with the reactants on the left and the products on the right-hand side. For example, the reaction between Rh-103 and a proton to produce Pd-103 and an emitted neutron is written as:
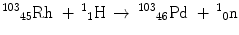
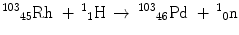
More frequently a short-hand notation is used where the incident and emitted particles are written in parentheses or brackets between the initial and final nuclei. Atomic numbers are omitted. Thus, the above reaction is abbreviated 103Rh[p, n]103Pd. Elementary particles and certain light nuclides have their own symbols, such as n, p, d, t, α, γ, β, e, π representing the neutron, proton, deuteron (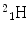
), triton (
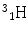), alpha particle (
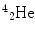), gamma ray, beta particle, electron, and pi meson, respectively.
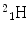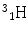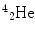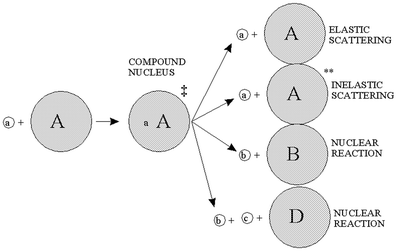
), triton (), alpha particle (), gamma ray, beta particle, electron, and pi meson, respectively.A complete detailed theory of nuclear reactions in terms of basic nuclear forces is not yet available. Instead, approximate treatments based on models are used for understanding measurements and have proved useful for predictive purposes. An early model useful to radionuclide production reactions was the compound nucleus model, introduced by Niels Bohr in 1936 (Bohr 1936), depicted in Fig. 3. In this model, the incident particle is absorbed into the nucleus of the target materials and the energy is distributed throughout the compound nucleus. In essence, the nucleus comes to some form of equilibrium before decomposing with the emission of particles. These two steps are considered to be independent of one another. It does not matter how the compound nucleus got to the high energy state; the evaporation of the particles will be independent of the way in which it was formed.
The nuclear reaction cross-section represents the total probability that a compound nucleus will be formed and that it will decompose in a particular channel. There is a minimum energy below which a nuclear reaction will not occur except by tunneling effects. The incident particle energy must be sufficient to overcome the Coulomb barrier and to overcome a negative energy of the reaction. Particles with energies below this barrier have a very low probability of reacting. The energy required to induce a nuclear reaction increases as the Z of the target material increases. For many low Z materials it is possible to use a low energy accelerator, but for high Z materials, it is necessary to increase the particle energy (Deconninick 1978).
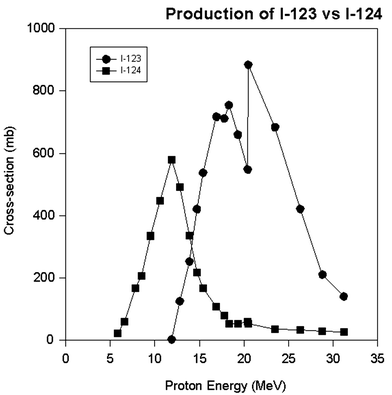
The various above phenomena lead to a disappointing fact in radionuclide production. It is not always possible to eliminate the radionuclidic impurities even with the highest isotopic enrichment and the widest energy selection, especially using chemical methodology in cases where the radionuclide impurities are isotopes with the same proton number and the electronic structure. An example of this is given in Fig. 4 for the production of iodine-123 with a minimum of I-124 impurity (Guillaume et al. 1975; Lambrecht and Wolf 1973; Qaim and Stocklin 1983). As can be seen from this figure, it is almost impossible to eliminate the I-124 impurity from the I-123 because the I-124 is being made at the same energy, and the chemical properties defined by the electronic structure are the same. All that can be done is to minimize the I-124 impurity by choosing an energy level where the production of I-124 is near a minimum. In this specific case, proton energy higher than ~20 MeV will give a minimum of I-124 impurity. This kind of an exercise is encountered in just about all situations with the production of medical radionuclides.
Fission is a special mode of nuclear de-excitation in the region of high atomic numbers. In spontaneous fission, the mutual electrostatic repulsion between protons of a very heavy nucleus can overcome the Coulomb barrier and causes the separation of a heavy nucleus into two lighter positively charged fragments, usually of unequal mass. There are over 60 known nuclides, which can spontaneously fission. For particle-induced fission, the bombarding particle supplies enough energy to overcome the barrier. In particular, thermal neutron fission of U-235 has had great significance for society. The 200 MeV energy release per reaction and release of an excess of neutrons made possible the development of both the atomic bomb and the nuclear reactor. Over 75 useful radionuclides are produced in this manner and are called fission products. Many of these can be separated and purified for medical, industrial, and research applications. Of interest for nuclear medicine are the light fragments resulting from induced fission, especially the fission products Mo-99, I-131 and Xenon-133. The production of Mo-99 has been of paramount importance to nuclear medicine. Molybdenum-99 is not directly used, but serves as the parent radionuclide for the daughter Tc-99m, now used diagnostically in over 85 % of all diagnostic imaging procedures in nuclear medicine worldwide (Richards et al. 1982). Iodine-131 is widely used to treat thyroid cancer and hyperactive thyroid conditions. Xenon-133 is used for studies of pulmonary ventilation and also for cerebral blood perfusion.
The compound nucleus model does not very well explain all the nuclear reaction processes. Some of these processes are characterized by direct interactions, where the incident particle collides with only one or a few nucleons in the target which are immediately ejected without sharing of energy throughout the nucleus. These “knock-on” reactions become increasingly important at bombarding energies of over about 40 MeV. Above about 100 MeV, collision with an individual nucleon is the most likely initial event, followed by its ejection from the nucleus. While passing through the nucleus this nucleon may in turn collide and eject another nucleon, leading to many successive nucleon–nucleon collisions. Some of these nucleons promptly escape while others undergo additional collisions in the nucleus. This “intranuclear cascade” is very rapid (duration ~10−22 s) and leaves the nucleus in a generally excited state from which it can lose more nucleons by evaporation. The sum of these interactions: knock-on; intranuclear cascade; and evaporation, is called the spallation process. Proton-induced spallation or breakup, has been used to produce a few radionuclides of interest to nuclear medicine, for example Xe-127, and Strontium-82. Although high-energy neutrons can also interact by a spallation process (Mirzadeh et al. 1983) due to lack of high intensity fast neutron sources, radionuclide production by neutron-induced spallation is much more limited.
It is important that the total excitation energy of a compound nucleus formed by absorption of a thermal neutron is just above the energy to bind a neutron in the compound nucleus. Thus, the time before statistical fluctuation can concentrate enough energy on a single neutron to cause its ejection from the nucleus, would be quite long. As a result, de-excitation by γ emission is much more likely and the main reaction with thermal neutrons is the n, γ (neutron in, gamma out) process.
2.2 Production Equation
The production of a given radionuclide is proportional to the number of target nuclei N t , number of incident particles φ and the reaction cross-section σ, or R = N t φσ. The product radionuclide itself undergoes radioactive decay, λN p . Thus, the net rate of change in the number of radioactive product nuclei, N p , during irradiation is given by the rate of formation less the rate of decay, or
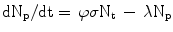
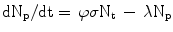
Since N t is so large as to remain essentially constant during irradiation, the solution to this differential equation is
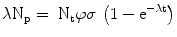
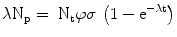
The activity of the product A p at the end of bombardment (EOB) is λN p , and after substitution we obtain the radionuclide production equation,
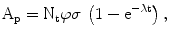where, A = activity in disintegrations per second, dps
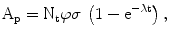
N t = number of target atoms = W/M × F × Avog
W = sample weight in grams,
M = atomic weight in grams/mole;
F = isotopic abundance, Avog = Avogadro’s number;
6.023 × 1023 atoms per mole]
φ = neutron flux in neutrons.cm−2.sec−1
σ = cross-section in cm2
λ = decay constant of product = ln(2)/t1/2
t = irradiation time
Note that at long irradiation times where λt ≫ 1 (or t irrad ≫ t ½ of the product) the factor (1−e−λt ) approaches 1. This signifies that the rate of product formation and the rate of product decay are equal, and the reaction is said to be at “saturation”. The term (1−e−λt ) is also known as the saturation factor. Thus, longer irradiation time does not produce any more radioactivity. In practice, irradiations longer than one half-life (“half saturation”) are relatively inefficient since doubling the irradiation by another half-life only increases radioactivity from 50 to 75 % of saturation.
As an example of the use of the production equation, consider a 24-h irradiation of 1 mg of natural rhenium (37.4 % Re-185) in a thermal neutron flux of 2 × 1014 n cm−2.sec−1 to make Re-186 (t 1/2 = 3.718 days). The tabulated cross-section is 112 barns (Mughabgab et al. 1984).
N t = (0.001 g/186.21 gm per mole)(0.374 natural Re)(6.023 × 1023 atoms/mole) = 1.21 × 1018 atoms
Then, the amount of Re-186 radioactivity produced is
A = (1.21 × 1018 atoms)(2 × 1014 n.cm−2.sec−1)(112 × 10−24 cm2) ×
[1-exp((−0.693/3.718 × 24 h) × 24 h)]
= 4.6 × 109 atoms per second, or disintegrations per second (dps)
= 124.3 mCi (1 mCi = 3.7 × 104 dps, or 37 MBq).
Corrections to this result would be needed if the samples were large, or the irradiation was lengthened. For a massive target with a high cross-section, there is sufficient absorption of neutrons in outer layers so that the effective neutron flux in the interior of the target is reduced (self-shielding). This effect is difficult to calculate and is usually measured. Also, Re-186 itself can absorb a neutron and convert into Rhenium-187. This process is called product burn-up. While some conversion of Re-185 into Re-186 can also be induced by higher energy neutrons, most comes from the thermal neutrons considered here because thermal neutron fluxes are usually much larger than for higher energy neutrons.
The production equation can take one of two forms, depending upon whether the target is immersed in a bath of neutrons as in a nuclear reactor, or irradiated in a specific direction by a beam of particles from an accelerator. In the latter case, the target is usually larger than the diameter of the beam. The fraction of target irradiated is then important. An early detailed discussion of the equations governing the production of radionuclides, in particular with reactors, is presented in the article by Mirzadeh and Walsh (Mirzadeh and Walsh 1998).
2.3 Sources of Nuclear Particles
2.3.1 Nuclear Fission Reactor
Although there are neutron sources based on natural radioactivity and accelerators, the most generally useful source of neutrons for radionuclide production is the research nuclear reactor. A reactor consists of an amount of fissionable material, either U-235 (natural or enriched), Pu-239, or U-233, assembled so that a controlled, self-sustaining chain reaction of neutron-induced fissions is maintained. The fission of U-235 produces an average of 2.4 neutrons, two medium mass nuclei (fission products with average masses of 100 and 140 amu), and the release of approximately 200 MeV. Since fission is best induced with low energy neutrons, a moderator (usually water) is used to slow the emitted neutrons. Some neutrons are absorbed by the moderator and structural materials and some escape. A chain reaction can be sustained if at least one of the neutrons causes another U-235 to fission. This condition is expressed as the multiplicity factor k and a reactor is “critical” at k = 1. The U-235 is usually embedded in high melting zirconium hydride contained in metal tubes bundled together into fuel elements. The arrangement of fuel elements is called the core.
At steady state, k is kept at 1 but sometimes k must be made larger than 1. This allows the neutron flux and the power level to be varied, and compensates for fuel use (burn up), build-up of neutron-absorbing fission products, and the deliberate introduction of samples that absorb neutrons. The quantity (k−1)/k is called the reactivity, and reactors must be designed with excess reactivity. The reactivity and power level are determined by the position of control rods. These control rods are made of materials with large neutron capture cross-sections, such as boron, cadmium, and hafnium. Lowering control rods into the core reduces the number of neutrons available for fission. Some specially designed reactors control reactivity by moving the fuel elements themselves.
The most important fission product from the point of view of reactor operation is Xenon-135. It has a half-life of 9.1 h and a neutron capture cross-section of 2.6 × 106 barns (b), the largest known. During steady-state reactor operation the build-up of Xe-135 is slow. However, upon shutdown the amount of Xe-135 initially increases rapidly due to grow-in from the decay of its parent, I-135 (t 1/2 = 6.6 h) and the decrease in (n, γ) reactions which destroy it. This Xe-135 “poisoning” peaks about 10 h after shutdown, and causes a large drop in reactivity (as much as 30 %). Since many reactors cannot overcome this much loss of reactivity, usually there is a period after shutdown during which the reactor cannot be restarted.
A nuclear reactor produces neutrons with a spectrum of energies up to about 20 MeV; the most probable energy of neutrons emitted in the fission process is 1.5 MeV. Neutrons are generally grouped into three categories, thermal neutrons (E n < 0.4 eV), epithermal neutrons (0.4 eV < E n < 100 keV), and fast neutrons (E n > 100 keV). The energy spectrum of the lowest energy neutrons approximates a Maxwellian distribution similar to that of ordinary gas molecules in equilibrium at room temperature; thus the name thermal neutrons. The peak of this distribution is at 0.025 eV. These neutrons are very efficient at producing nuclear reactions and are widely used for radionuclide production on a commercial basis. Epithermal (or resonance) neutrons are formed when fast neutrons are partially slowed down by collisions with moderator. The fast neutrons arise from the fission process directly.
The use of reactors for power production is based on the large 200 MeV energy release per fission. Approximately 1 g/day of fissioned fuel produces 1 mw of reactor thermal power. Electrical output is only about one-third of the thermal power. Further discussion of reactor physics, safety and economics is beyond the scope of this chapter, but many references exist (Liverhaut 1960; Glasstone and Sesonske 1963; Cohen 1977).
Electrical power generation is generally incompatible with radionuclide production, so it is the research reactor which is of most interest here. These can take many different forms, but the vast majority of these have used enriched U-235 for fuel, with enrichment varying from 10 % to greater than 90 %. These typically thermalize the neutrons with moderators of water, D2O, or graphite. Power levels cover the range from 0.1 W (e.g., Aerojet General Corp. Teaching Reactor AGN-20) to 450 MW (Fast Flux Test Facility, Westinghouse Hanford Company, now shut down). Useable thermal neutron fluxes range from 5 × 106 n cm−2 s−1 to ~2 × 1015 n cm−2 s−1. A summary of the maximum fluxes available at nine of the principal research reactors in the United States is given in Table 4.
Table 4
Principal research reactors in the United States
Reactor/Institution | Operating power (MW) (1–16 MeV) | Thermal | Neutron flux epithermal (0–0.25 eV) | Fast (0.25 eV–1 MeV) |
|---|---|---|---|---|
Fast flux test facilitya, Westinghouse Hanford Company | 450 | 5.2 × 1014 | 6.6 × 1015 | 3.7 × 1014 |
Advanced test reactor, Idaho National Engineering Laboratory | 250 | 4.5 × 1014 | 6.7 × 1014 | 4.1 × 1014 |
High flux isotope reactor, Oak Ridge National Laboratory | 85 | 5.3 × 1015 | 1.5 × 1015 | 5.8 × 1014 |
High flux beam reactora, Brookhaven National Laboratory | 30 | 4.2 × 1014 | 1.3 × 1015 | 1.5 × 1014 |
Missouri University research reactor, University of Missouri | 10 | 4.2 × 1014 | 1.6 × 1014 | 7.0 × 1014 |
Omega west reactora, Los Alamos National Laboratory | 8 | 9.0 × 1013 | 5.0 × 1012 | __ |
Georgia Institute of Technology Research Reactor | 5 | 6.5 × 1013 | 1.7 × 1012 | 2.9 × 1012 |
Massachusetts Institute of Technology, Reactor | 5 | 6.0 × 1013 | .3.0 × 1013 | 1 × 1013 |
Oregon State University Triga Reactor | 1 | 1.0 × 1013 | 4.0 × 1011 | __ |
Most research reactors have the entire core immersed in water (or D2O) and are often called swimming pool reactors. The 5–8 m of water functions not only as a moderator, but also for cooling and radiation shielding. Irradiation positions for samples typically exist between fuel rods (in-core locations) or in an annular region just inside a ring of low Z material with small neutron capture cross-section. This material (beryllium is often used) “reflects” neutrons back to the core and minimizes neutron losses. The reflector increases thermal neutron flux at irradiation stations and helps save fuel. The actual fluxes and neutron energies available for radionuclide production are a sensitive function of the detailed reactor design and vary with location within the reactor. A brief description of ORNL-HFIR and other major research reactors in the US has been provided in the article by Mausner and Mirzadeh (Mausner and Mirzadeh 2003).
2.3.2 Charged Particle Accelerators
In general, there are four major reasons that accelerator-produced radionuclides are used more widely than reactor-produced radionuclides: (1) The radionuclides produced in a reactor may have unfavorable decay characteristics (particle emission, half-life, gamma rays, etc.) for a particular application; (2) The radionuclide cannot usually be produced in a reactor with high specific activity; (3) Access to a reactor is limited; and, perhaps most importantly; (4) The radionuclide can be produced most efficiently and in a more cost-effective manner in an accelerator. In addition, of late, the number of reactors available has become much fewer than the number of cyclotrons available to the scientific and industrial community.
There are a wide variety of nuclear reactions, which are involved in the accelerator production of radionuclides. These are very similar in principle with those discussed in Sect. 2.1 above. Nuclear reactions specific to accelerator production have been described and covered in detail by David Schlyer of BNL (Schlyer 2003).
The bombarding particles are usually protons, deuterons, or helium particles. The energies which are used range from a few MeV to hundreds of MeV (Gandarias-Cruz and Okamoto 1988). In these situations, one of the most useful models for nuclear reactions is also the compound nucleus model originally introduced by Bohr in 1936 (Bohr 1936), and described in Sect. 2.1 (Fig. 3].
One of the main concerns in targets, specifically in accelerator production, is the deposition of power in the material during irradiation (Schlyer 2003). If the power deposited exceeds the ability of the target to remove the heat, the target will eventually be destroyed or the target material will be melted, volatilized, or reduced in density to the point where the yield will be drastically reduced. In liquid targets the material may boil and thereby reduce the average density. In gaseous targets, the density of the gas is reduced in the beam strike area. All these effects are a result of the increased temperature in the beam strike area and this in turn is a result of the power deposited by the beam as it passes through matter. The power deposited in the material is the beam current in microamps (μA) multiplied by the energy loss in MeV and the result is the number of watts deposited.
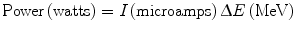
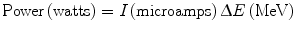
The exact position of the heat deposition will depend on the dE/dx (stopping power) of the beam in the target material with most of the heat being deposited near the end of the particle range in the Bragg peak. A simple approximation for the stopping power is given by the relation:
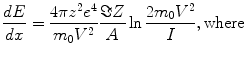
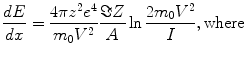
dE/dx = energy loss per unit length
z = the atomic number of the projectile
e = elementary charge 4.803 × 10−10 (erg-cm)1/2
m 0 = the electron rest mass
V = relativistic projectile velocity
A = Avogadro’s number
Z = atomic number of the target material
I = adjusted ionization potential of the target material.
The stopping power of particles other than protons is given by the relationships:
deuterons S d (E) = S p (E/2)
tritons S t (E) = S p (E/3)
3He S t (E) = 4S p (E/3)
4He S t (E) = 4S p (E/4)
In order to have a useful accelerator target for the production of a radionuclide, it is necessary to effectively remove the heat generated by the passage of the beam. There are three modes of heat transfer which are active in targets. These are conduction, convection, and radiation. Radiation is only a significant mode of heat loss at high temperatures (>500° C). Gases and liquids can transfer heat via convection and conduction. In most targets, the final removal of the heat will be from a backing plate to a flowing water stream. Heat transfer in solids is somewhat simpler than in other media since the heat usually flows through the target matrix mainly by conduction. Once the heat has been transferred to the cooled surface of the target, the heat will usually be removed by a fluid such as water flowing against the back of the target.
The transfer of the heat through the target material, and through the backing material, is fairly straightforward. The real surprises in designing solid targets come from the interfaces where the target material meets the backing material. This is where many problems arise and the better the connection one can make at this interface, the better the heat transfer will be. Problems with loss of target material or damage to the target during the irradiation will be less likely.
3 Reactor Production Using Neutrons
Table 5 lists some of the reactor-produced radionuclides important to therapeutic nuclear medicine. There are three general reaction types used: (a) neutron capture, [n, γ]; (b) neutron capture followed by decay; and (c) fission. The most widely used route is the [n, γ] reaction with thermal neutrons. The advantage of this production process is its simplicity and high yield. It is straightforward in that in many cases elemental targets may be used and no chemical separation of target and product is required (or possible). Since cross-sections tend to be higher than most other reaction types, yields are generally good. The primary disadvantage of this reaction also relates to the fact that the radioactive product cannot be separated from the target. Thus, stable atoms dilute the radioactive atoms and the specific activity will be much lower than that of “carrier-free” or NCA radionuclide. Radioimpurities may arise from [n, γ] reactions on other isotopic forms of the target or chemical impurities in the target. The use of isotopically enriched targets can minimize production of impurities and improve yield, but often at rather high costs. Nevertheless, enriched targets are essential if the natural abundance of the target isotope is low and significant impurities are co-produced.
Table 5
Radionuclides of current or potential use in therapy produced in nuclear reactors
T½ | Nuclear reaction | Cross section (b) | Target | |
|---|---|---|---|---|
32P | 14.3 days | 31P(n, γ), 32S(n, p) | 0.18, 0.06 | KH2PO4, sulfur |
35S | 87.5 days | 35Cl(n, p) | 0.49 | KCl |
64Cu | 12.7 h | 63Cu(n, γ) | 4.50 | Enriched 63Cu |
64Zn(n, p) | 0.039 | Enriched 64Zn | ||
67Cu | 2.6 days | 67Zn(n, p) | 0.001 | Enriched 67Zn |
75Se | 119.8 days | 74Se(n, γ) | 48.0 | Enriched 74Se |
89Sr | 50.5 days | 88Sr(n, γ) | 0.82 | Enriched 88Sr2O3 |
90Y | 64.0 h | 235U(n, f)90Sr 90Sr(β– decay) | NA | Enriched 235U |
103Pd | 16.99 days | 102Pd(n, γ) | 3.4 | Enriched 102Pd |
117mSn | 13.6 days | 117Sn(n, n′γ) | 0.22 | Enriched 117Sn |
114mIn | 49.5 days | 113In(n, γ) | 8.1 | Enriched 113In |
125I | 60.1 days | 124Xe(n, γ)125Xe (ECdecay) | >28.0a | Enriched 124Xe |
131I | 8.04 days | 130Te(n, γ) | 0.29 | Enriched 130Te |
235U(n, f) | 268† | Enriched 235U | ||
153Sm | 1.9 days
Related posts: Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
Get Clinical Tree app for offline access
|
