) [6] using approximately 1 / 10th the energy [3] of current shock protocols when low-energy pulses are used.
The exact nature of the fine-scale structural heterogeneity driving virtual-electrode formation during defibrillation has been suggested to be blood vessels [3, 4, 7] and/or endocardial trabeculae invaginations (insertion site into the endocardial surface) [5, 8]. Detailed theoretical analysis has also suggested virtual electrodes may form on the outer ‘tip’ of a trabecular or papillary muscle where curvature is negative [9]. Endocardial trabeculae have been shown to effectively contain wave-front filaments in 3D high-resolution monodomain simulations of the rabbit ventricles, for relatively longer periods (than other anatomical structures) [10], making these structures important for defibrillation. However, a detailed understanding of these phenomena is still lacking. In particular, how geometrical factors relating to the size, relative curvature and proximity of neighbouring trabeculations affect the formation of virtual electrodes is not well understood. Such knowledge may be key when considering known significant inter-species differences in endocardial anatomy and differences in spatial scales when applying these findings to the human ventricle. In this study, we perform such a detailed investigation into how the specific nature of the endocardial surface geometry affects the field strength required to generate a propagated AP from surface virtual electrodes, and demonstrate the importance of the surrounding conductive media on these effects.
2 Methods
Computational Methods. The bidomain equations, stated in parabolic form for isotropic conductivities, are
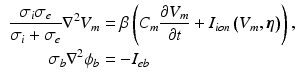
where 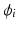 and
and 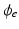 are the intra and extra-cellular potentials,
are the intra and extra-cellular potentials, 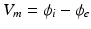 is the transmembrane potential,
is the transmembrane potential, 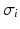 and
and 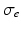 are the intra and extra-cellular conductivities,
are the intra and extra-cellular conductivities, 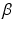 is the membrane surface area to volume ratio,
is the membrane surface area to volume ratio, 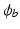 is the bath potential,
is the bath potential, 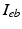 is the extracellular current stimuli applied to the bath-space,
is the extracellular current stimuli applied to the bath-space, 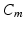 is the membrane capacitance per unit area and
is the membrane capacitance per unit area and 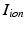 is the membrane ionic current density, as a function of the transmembrane potential
is the membrane ionic current density, as a function of the transmembrane potential 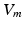 and the vector of state variables
and the vector of state variables 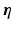 . The boundary conditions for (1) are
. The boundary conditions for (1) are
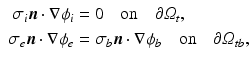
where the subscripts t and tb mean the tissue and tissue-bath interface respectively and 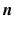 is the unit-normal vector to the tissue. The linear finite element solver Cardiac Arrhythmia Research Package [11] (CARP) was used to solve (1). The harmonic mean (
is the unit-normal vector to the tissue. The linear finite element solver Cardiac Arrhythmia Research Package [11] (CARP) was used to solve (1). The harmonic mean (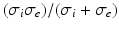 ) conductivity was 0.0176 S/m [12] and the bath conductivity (
) conductivity was 0.0176 S/m [12] and the bath conductivity (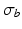 ) was 1.0 S/m.
) was 1.0 S/m.
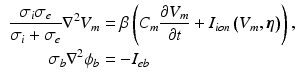
(1)
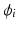 and
and 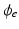 are the intra and extra-cellular potentials,
are the intra and extra-cellular potentials, 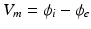 is the transmembrane potential,
is the transmembrane potential, 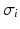 and
and 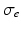 are the intra and extra-cellular conductivities,
are the intra and extra-cellular conductivities, 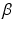 is the membrane surface area to volume ratio,
is the membrane surface area to volume ratio, 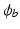 is the bath potential,
is the bath potential, 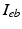 is the extracellular current stimuli applied to the bath-space,
is the extracellular current stimuli applied to the bath-space, 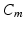 is the membrane capacitance per unit area and
is the membrane capacitance per unit area and 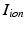 is the membrane ionic current density, as a function of the transmembrane potential
is the membrane ionic current density, as a function of the transmembrane potential 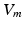 and the vector of state variables
and the vector of state variables 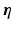 . The boundary conditions for (1) are
. The boundary conditions for (1) are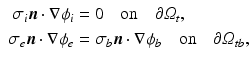
(2)
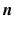 is the unit-normal vector to the tissue. The linear finite element solver Cardiac Arrhythmia Research Package [11] (CARP) was used to solve (1). The harmonic mean (
is the unit-normal vector to the tissue. The linear finite element solver Cardiac Arrhythmia Research Package [11] (CARP) was used to solve (1). The harmonic mean (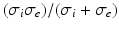 ) conductivity was 0.0176 S/m [12] and the bath conductivity (
) conductivity was 0.0176 S/m [12] and the bath conductivity (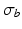 ) was 1.0 S/m.
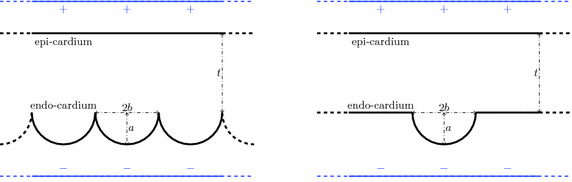
) was 1.0 S/m.Computational Models. In order to elicit meaningful results, the dimensionality is restricted to 2D and the endocardial surface is assumed to have a highly idealized geometry consisting of periodic ellipsoids (representing endocardial trabeculations) or a single ellipsoid (representing a single trabeculation). In this initial study, geometries are based-on rabbit right ventricular MR data [7]. It is further assumed that the epicardial surface has a straight edge. Figure 1 shows a schematic of the geometries used. In the case of multiple trabeculae, each equivalent point along the surface of an individual trabeculation may be represented by the period (i.e. the angle subtended with the positive horizontal), between 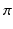 and
and 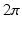 . Differences in curvature were obtained by varying the semi-minor (b) and semi-major (a) axes of the semi-ellipsoids representing the trabeculations. In this work we keep t and a constant at
. Differences in curvature were obtained by varying the semi-minor (b) and semi-major (a) axes of the semi-ellipsoids representing the trabeculations. In this work we keep t and a constant at 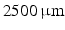 and
and 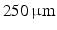 respectively and vary b in
respectively and vary b in 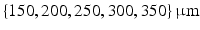 . Unstructured triangular meshes of the geometries shown in Fig. 1 were created with a maximum element edge length of
. Unstructured triangular meshes of the geometries shown in Fig. 1 were created with a maximum element edge length of 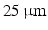 , with local element refinement around cusps and other sharp changes in curvature.
, with local element refinement around cusps and other sharp changes in curvature.
 and
and  . Differences in curvature were obtained by varying the semi-minor (b) and semi-major (a) axes of the semi-ellipsoids representing the trabeculations. In this work we keep t and a constant at
. Differences in curvature were obtained by varying the semi-minor (b) and semi-major (a) axes of the semi-ellipsoids representing the trabeculations. In this work we keep t and a constant at 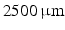 and
and 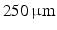 respectively and vary b in
respectively and vary b in 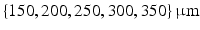 . Unstructured triangular meshes of the geometries shown in Fig. 1 were created with a maximum element edge length of
. Unstructured triangular meshes of the geometries shown in Fig. 1 were created with a maximum element edge length of 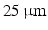 , with local element refinement around cusps and other sharp changes in curvature.
, with local element refinement around cusps and other sharp changes in curvature.
Fig. 1.
Computational geometries used to represent multiple, periodic (left) and single (right) trabeculations. The semi-major and -minor axes are a and b, respectively. Electrode locations are shown in blue. t is tissue thickness (Color figure online).
Extra-cellular fields were applied between the electrodes shown in Fig. 1 of varying strength, of duration 2 ms. A bisection search algorithm was implemented to find the minimum applied electrode potential difference (accurate to 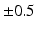 mV) to elicit a propagated AP from any point on the curved boundary. Throughout,
mV) to elicit a propagated AP from any point on the curved boundary. Throughout, 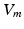 and
and 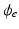 were computed at all points within the domain.
were computed at all points within the domain.
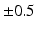 mV) to elicit a propagated AP from any point on the curved boundary. Throughout,
mV) to elicit a propagated AP from any point on the curved boundary. Throughout, 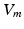 and
and 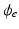 were computed at all points within the domain.
were computed at all points within the domain.3 Results
Figure 2 shows the variation in the minimum applied potential difference with semi-minor axis b for the single trabeculation (top) and multiple trabeculations (bottom) geometries. For all values of curvature, the minimum potential difference for propagation is consistently higher in the case of the single trabeculation, always requiring a field strength of ![$$>0.1$$” src=”/wp-content/uploads/2016/09/A339585_1_En_47_Chapter_IEq26.gif”></SPAN> V greater than the case of multiple structures. In both geometries, as <SPAN class=EmphasisTypeItalic>b</SPAN> increases, there is a monotonic decrease in the minimum potential difference required for AP propagation from any point on the endocardial surface, with a relatively faster decrease seen in the case of the single trabeculation.<br />
<DIV id=Fig2 class=Figure><br />
<DIV id=MO6 class=MediaObject><IMG alt=A339585_1_En_47_Fig2_HTML.gif src=]()
Fig. 2.