Fig. 19.1
Jablonski diagrams for 1 photon fluorescence, 2PF and SHG. GS = ground state; ES = excited state; Δt = excited state lifetime
To explore the origin of SHG requires consideration of how the light interacts with the non-linear optical material. A qualitative approach will provide a physical understanding of the process and why it is fundamentally so different from fluorescence. Much as when a guitar string is plucked too hard, if an intense pulse of light interacts with a material, it can interact with the electrons in that material and emerge with additional harmonics. The ability of the oscillating electric field in the light wave to interact with the material depends on its polarisability. We can understand how this might produce harmonics of the original fundamental frequency by referring to Fig. 19.2. A high amplitude electromagnetic wave impinges on an array of molecules that are oriented with their electron clouds aligned so as to reinforce the light wave for the positive component of the oscillating electric filed and oppose the negative electric field component. The emerging electromagnetic wave is correspondingly distorted and can be decomposed into components that correspond to the fundamental frequency plus a component at double that frequency. It is apparent from this simple picture that SHG depends on the collective properties of the array; this distinguishes it from absorbance and fluorescence, which depend on the interaction of photons with individual molecules. Reference to Fig. 19.2 makes it easy to understand why a fully centrosymmetric array of molecules or randomly oriented molecules in a homogeneous solution cannot produce SHG: it is because the electric field vector of the fundamental light wave would not be differentially distorted, as it is in Fig. 19.2 for an ordered array. One can also appreciate from this picture that the SHG will depend strongly on the polarization of the incoming light and its angle of incidence with respect to the array of harmonophores in the non-linear optical material—i.e. tensor relationships. Thus while this simple picture cannot fully describe the details of SHG, it nicely explains many qualitative features of the phenomenon.
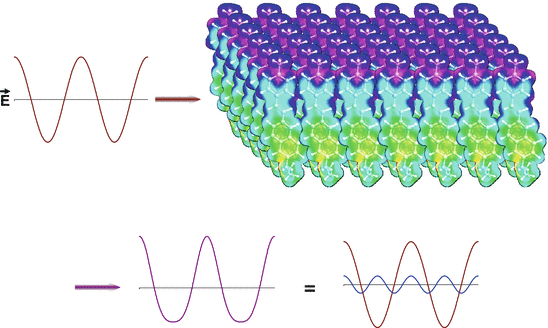

Fig. 19.2
Qualitative picture of the optical physics underlying SHG. The oscillating electric field of the intense fundamental light beam (red sine wave on the top left) impinges on an ordered array of polarizable molecules. The interaction of the oscillating wave with the material induces a distortion of the emergent light wave (violet, bottom left), that is equivalent to the mixing of the original fundamental frequency with a small contribution from twice the frequency, i.e. the second harmonic (shown in blue on the bottom right). The molecular array shown in the upper right was created by 2D translations of an electron density map of the aminonaphthylethenylpyridinium (ANEP) chromophore. The electron density map was rendered in colors from the output of molecular orbital calculations
With this qualitative picture in hand, it is worthwhile to consider the photophysics at a more rigorous level in order to appreciate some of the more subtle features of SHG and how it differs from 2PF. Such a treatment necessarily begins with the general expression for polarisability, which can be expressed as a Taylor series in the electric field: 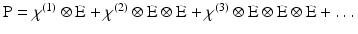
P is the induced polarisation vector, E represents the vector electric field, χ(i) is the ith-order non-linear susceptibility tensor and  represents a combined tensor product and integral over frequencies. It is again important to emphasize that the χ(i) are bulk properties of the material. However, they parallel the interaction of an electric field with molecules based on the molecular properties, respectively, of dipole moment, and polarizability and hyperpolarisabilities (Cole and Kreiling 2002; Moreaux et al. 2000a; Williams 1984). The first term in the series describes normal absorption and reflection of light. The second- and third-order terms correspond to the phenomena of SHG and 2PF and their sensitivity to electric field. To begin to appreciate how SHG might directly depend on the electric field associated with the membrane potential in addition to the oscillating electric field of the light, one can decompose the above equation into a combination of a true second-order process and a third-order process dependent on a constant electric field:
represents a combined tensor product and integral over frequencies. It is again important to emphasize that the χ(i) are bulk properties of the material. However, they parallel the interaction of an electric field with molecules based on the molecular properties, respectively, of dipole moment, and polarizability and hyperpolarisabilities (Cole and Kreiling 2002; Moreaux et al. 2000a; Williams 1984). The first term in the series describes normal absorption and reflection of light. The second- and third-order terms correspond to the phenomena of SHG and 2PF and their sensitivity to electric field. To begin to appreciate how SHG might directly depend on the electric field associated with the membrane potential in addition to the oscillating electric field of the light, one can decompose the above equation into a combination of a true second-order process and a third-order process dependent on a constant electric field:
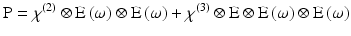
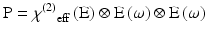
Here, χ(2) eff(E) is an effective second-order non-linear susceptibility (Conboy and Richmond 1997; Yan et al. 1998) that depends on a static electric field vector, E. This term could impart a membrane potential sensitivity for harmonophores embedded on one side of a cell membrane.
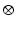 represents a combined tensor product and integral over frequencies. It is again important to emphasize that the χ(i) are bulk properties of the material. However, they parallel the interaction of an electric field with molecules based on the molecular properties, respectively, of dipole moment, and polarizability and hyperpolarisabilities (Cole and Kreiling 2002; Moreaux et al. 2000a; Williams 1984). The first term in the series describes normal absorption and reflection of light. The second- and third-order terms correspond to the phenomena of SHG and 2PF and their sensitivity to electric field. To begin to appreciate how SHG might directly depend on the electric field associated with the membrane potential in addition to the oscillating electric field of the light, one can decompose the above equation into a combination of a true second-order process and a third-order process dependent on a constant electric field:
represents a combined tensor product and integral over frequencies. It is again important to emphasize that the χ(i) are bulk properties of the material. However, they parallel the interaction of an electric field with molecules based on the molecular properties, respectively, of dipole moment, and polarizability and hyperpolarisabilities (Cole and Kreiling 2002; Moreaux et al. 2000a; Williams 1984). The first term in the series describes normal absorption and reflection of light. The second- and third-order terms correspond to the phenomena of SHG and 2PF and their sensitivity to electric field. To begin to appreciate how SHG might directly depend on the electric field associated with the membrane potential in addition to the oscillating electric field of the light, one can decompose the above equation into a combination of a true second-order process and a third-order process dependent on a constant electric field: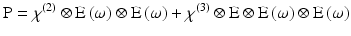
(19.1)
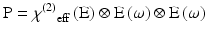
(19.2)
The SHG intensity, I(2ν), is related to the square of the second order non-linear susceptibility, χ(2) (or χ(2) eff(E)):
![$$ I\left(2\nu \right)\propto \frac{{\left[{\chi}^{(2)}I\left(\nu \right)\right]}^2}{\tau } $$](/wp-content/uploads/2016/09/A320817_1_En_19_Chapter_Equ3.gif)
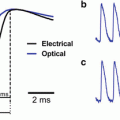
where I(ν) is the laser pulse energy, ν is the fundamental frequency and 2ν is the second harmonic frequency. As in 2PF, the signal has a quadratic dependence on laser intensity and an inverse dependence on pulsewidth, τ, but since SHG is an instantaneous process, signal will only be generated during the duration of the laser pulse.
![$$ I\left(2\nu \right)\propto \frac{{\left[{\chi}^{(2)}I\left(\nu \right)\right]}^2}{\tau } $$](/wp-content/uploads/2016/09/A320817_1_En_19_Chapter_Equ3.gif)
(19.3)
We now turn to a consideration of the molecular origin of SHG. χ(2) is related to the molecular property β, the first hyperpolarizability according to:
![$$ {\chi}^{(2)}={N}_s<\beta > $$” src=”/wp-content/uploads/2016/09/A320817_1_En_19_Chapter_Equ4.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(19.4)</DIV></DIV>where N<SUB>s</SUB> is the density of molecules and the brackets denotes an orientational average. This further underscores the need for a non-centrosymmetric region, since <ß> would vanish for an isotropic distribution. Examination of Eqs. (<SPAN class=InternalRef><A href=]() 19.3) and (19.4) also reveals a major difference in the expected contrast for the 2PF and SHG signal levels: SHG depends on the square of the surface density whereas fluorescence intensity is linear with the density of fluorophores. This can lead to significant differences in these two mechanisms even when signal arises from the same dye in the membrane. For example, at high dye concentrations the fluorescence signal will become quenched due to dye aggregation and subsequent non-radiative decay, while the SHG would actually be larger due to the square dependency on the surface density. SHG can be resonance-enhanced when the second harmonic transition overlaps with an electronic absorption band. The resonance-enhanced molecular hyperpolarizability (Dirk et al. 1986; Morley 1988; Nicoud and Twieg 1987), which determines the resonance contribution, is given by:
19.3) and (19.4) also reveals a major difference in the expected contrast for the 2PF and SHG signal levels: SHG depends on the square of the surface density whereas fluorescence intensity is linear with the density of fluorophores. This can lead to significant differences in these two mechanisms even when signal arises from the same dye in the membrane. For example, at high dye concentrations the fluorescence signal will become quenched due to dye aggregation and subsequent non-radiative decay, while the SHG would actually be larger due to the square dependency on the surface density. SHG can be resonance-enhanced when the second harmonic transition overlaps with an electronic absorption band. The resonance-enhanced molecular hyperpolarizability (Dirk et al. 1986; Morley 1988; Nicoud and Twieg 1987), which determines the resonance contribution, is given by:
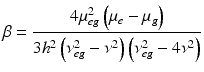
Where h is Planck’s constant, μg and μe are the dipole moments of the ground and excited states, respectively, μeg is the transition moment, ν is the frequency of the incident light, and hνeg is the energy for the electronic transition from the ground to the excited state. For the very broad absorption bands of organic dyes in solution, the resonance condition where 2ν overlaps νeg will pertain over a large range of wavelengths. Other consequences of this simple expression are that β is enhanced when there is a large difference in the ground and excited state electron distribution, i.e. a large μe − μg, and when the dye has a large extinction coefficient (which is proportional to μeg, the transition dipole). These are precisely the features that have been behind the design of our electrochromic styryl dyes and this is what led us to initially explore the possibility that they may produce large SHG signals This relationship between SHG and electrochromism manifest in Eqs. (19.2) and (19.5) was also the original motivation for us to explore whether SHG from membranes stained with our dyes could be sensitive to membrane potential.




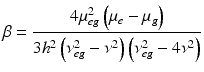
(19.5)
3 SHG Response to Membrane Potential
Our first foray into the non-linear optical properties of our dyes, involved creating a monolayer of di-4-ANEPPS in a Langmuir-Blodgett trough (Huang et al. 1988). In a series of papers that culminated in the first high resolution SHG images (Ben-Oren et al. 1996; Bouevitch et al. 1993; Campagnola et al. 1999), we were able to show that the SHG signal from ANEP dye stained membranes is sensitive to membrane potential. These experiments were continued (Campagnola et al. 2001; Clark et al. 2000; Millard et al. 2003a, b, 2004, 2005a, b; Teisseyre et al. 2007; Yan et al. 2006) and were validated and extended by the laboratories of Jerome Mertz, Rafael Yuste, Kenneth Eisenthal and Watt Webb (Araya et al. 2006, 2007; Dombeck et al. 2004, 2005; Jiang et al. 2007; Moreaux et al. 2000a, b, 2003; Nuriya et al. 2006; Pons et al. 2003).
Table 19.1, taken from a published paper (Teisseyre et al. 2007), summarizes results from a series of very promising new probes for both fluorescence and SHG. The absorbance and emission maxima in this Table are for dyes bound to lipid vesicles. The first three dyes in the Table are noteworthy because of the huge fluorescence sensitivities observed for them on the voltage clamped hemispherical bilayer (column 4; see Chap. 2 in this volume). Versions of these chromophores have been extraordinarily successful in fluorescence optical recording from brain slice and heart studies. A completely new class of hemicyanines employing an amino-thiophene donor moiety are the “PY” probes (for their inventor, Ping Yan) in the Table. We had employed thiophenes as linker moieties for many years, but this is the first set of hemicyanine chromophores that we are aware of where amino-thiophenes serve as the electron donor. The rationale for this donor moiety is that the thiophene behaves more like a rigidified diene than an aromatic heterocycle; thus through conjugation of the unshared electrons on the amino nitrogen is more effective than for the aniline and amino-naphthalene donor moieties in the earlier generation of dyes. Indeed, the spectra of these dyes are much further red shifted than comparable dyes employing aniline or amino-naphthalene donors. We also felt that these dyes should be particularly suitable for SHG imaging because the thiophenes are highly polarizable; additionally there should be a large change in dipole moment in going from ground to excited state for resonance enhanced SHG (Eq. 19.5). All of the dyes have absorbance maxima in the range of 530–560 nm in lipid membranes. This makes them ideal for SHG with our 1,064 nm femtosecond fiber laser and these dyes do indeed show strong SHG and the best SHG sensitivity to potential that we know of (PY-1278 is twice as good as FM-4-64). Also very striking is the 2-photon result shown for PY-1268 of 16.6 %/50 mV. It should be noted that all the results reported in columns 6 and 7 were for excitation with the 1,064 nm laser and emission at the 2 wavelength ranges indicated; no attempt was made to find optimal wavelengths for the 2PF sensitivity to potential, so most of these numbers are likely to be improvable. Indeed the 1-photon wavelength optima are generally quite different. A full account of the synthesis of this novel class of dyes has been published (Yan et al. 2008). A major problem that will need to be addressed for these dyes before they can be truly useful VSDs is their poor photostability (Zhou et al. 2007).
Table 19.1
Linear and non-linear responses of Gen3 dyes
Dye | 1PF Abs. Max (nm) | 1PF Em. Max (nm) | 1PF Change (ΔF/F − 100 mv); Ex/Em (nm) | SHG Change (%50 mV) | 2PF Change (%, 615 − 665 nm/50 mV) | 2PF Change (%, 750 − 850 nm/50 mV) | SHG Kinetics (ms) | Structure |
|---|---|---|---|---|---|---|---|---|
JPW-6008 di-4-ANEQPQ | 528 | 670 | 1.2E−001; 610/>665 | 3.84 ± 0.38 | 0.79 ± 0.37 | 5.03 ± 0.26 | 76 ± 13 |  |
JPW-6003 di-4-ANBDQPQ | 539 | 708 | 2.0E−001; 618/>715 | 3.55 ± 0.55 | −6.61 ± 0.88 | 4.32 ± 0.57 | <5 |  |
JPW-6027 di-4-ANHTQPQ | 504 | 655 | 5.4E−002; 630/>715 | 4.15 ± 0.28 | −7.51 ± 0.73 | 2.83 ± 0.45 | 34 ± 3 | 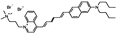 |
PY-1261 | 547 | 686 | 5.0E−002; 625/>715 | 9.56 ± 0.42 | −2.57 ± −0.24 | 5.22 ± 0.28 | <5 | 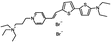 |
PY-1266 | 552 | 694 | 1.0E−001; 635/>715 | 3.75 ± 0.33 | −4.80 ± 0.53 | 2.25 ± 0.47 | 23 ± 2 | 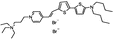 |
PY-1268 | 535 | 714 | 4.2E−002; 640/>715 | 1.82 ± 0.18 | −16.64 ± 0.85 | −4.28 ± 0.54 | <5 | 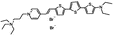 |
PY-1274 | 551 | 691 | 5.0E−002; 620/>715 | 5.65 ± 0.45 | −4.20 ± 0.13 | 3.12 ± 0.18 | – | 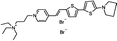 |
PY-1278 | 555 | 688 | 7.9E−002; 640/>715 | 10.70 ± 0.59 | −3.86 ± 0.53 | 6.52 ± 0.76 | <5 | 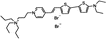 |
PY-1280 | 547 | 690 | 1.1E−001; 640/>715 | 10.13 ± 0.88 | −6.12 ± 0.87 | 5.77 ± 1.22 | 109 ± 30 | 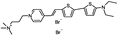 |
PY-1282 | 530 | 676 | 8.0E−002; 640/>715 | 11,64 ± 0.60 | 0.29 ± 0.39 | 8.78 ± 1.08 | 16 ± 1 | 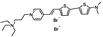 |
PY-1284 | 536 | 588 | 1.5E−002; 555/>610 | 6.18 ± 0.68 | 6.72 ± 0.58 | – | – | 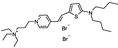 |
PY-1286 | 547 | 692 | 1.8E−001; 640/>715 | 8.09 ± 0.42 | −5.65 ± 0.50 | 3.51 ± 0.66 | 27 ± 1 | 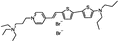 |
The labs of Rafael Yuste and Ken Eisenthal at Columbia U. have collaborated to perform SHG measurements of FM-4-64 applied to single neocortical pyramidal neurons through a patch pipette. FM-4-64 is a hemicyanine dye similar to our first generation styryl dyes in that it contains an aniline donor moiety (rather than an aminonaphthalene) conjugated via a trienyl linkage to a pyridinium acceptor. It has found extensive utility as a probe for synaptic vesicle cycling because it can be applied to preparations from the outside and readily becomes internalized in the vesicles. When applied from the inside, as in the Columbia experiments, the dye remains in the neuron because of its doubly positive charge; i.e. the negative resting potential of the cell will hold this relatively water soluble dye in the interior of the dendrite, where vesicle cycling is presumably non-existent. The Columbia group has published two papers in which they used SHG to measure electrical activity in individual spines (Araya et al. 2006; Nuriya et al. 2006) and they have used this and less direct experiments (Araya et al. 2007) to argue that the spine is indeed an electrical compartment.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree