Fig. 1.
Generating 100 segmentations using a default parameter set and increasing noise. Left: Distribution of algorithm parameters (normalised for comparison) for all experiments. Right: Comparison of physiological parameter accuracy and segmentation accuracy for all experiments; here stroke volume (SV) accuracy (A) is defined with respect to the Gold Standard (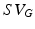 ) as follows:
) as follows: 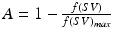 , where
, where 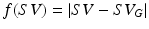 and
and 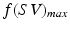 is the maximum f value obtained within this set. There are three pertinent things to note: (1) As the parameters become increasingly noisy, accuracy tends to drop, but there are still occasions which produce good results. (2) The ‘default’ parameter set is not necessarily the best one; but it’s difficult to predict a priori which one is. (3) Sets with even just one estimated physiological parameter being closer to the true value are visibly more likely to have higher accuracy; this is regardless of whether they originated from the less or more ‘noisy’ part of the experiment.
is the maximum f value obtained within this set. There are three pertinent things to note: (1) As the parameters become increasingly noisy, accuracy tends to drop, but there are still occasions which produce good results. (2) The ‘default’ parameter set is not necessarily the best one; but it’s difficult to predict a priori which one is. (3) Sets with even just one estimated physiological parameter being closer to the true value are visibly more likely to have higher accuracy; this is regardless of whether they originated from the less or more ‘noisy’ part of the experiment.
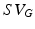 ) as follows:
) as follows: 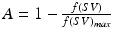 , where
, where 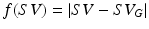 and
and 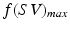 is the maximum f value obtained within this set. There are three pertinent things to note: (1) As the parameters become increasingly noisy, accuracy tends to drop, but there are still occasions which produce good results. (2) The ‘default’ parameter set is not necessarily the best one; but it’s difficult to predict a priori which one is. (3) Sets with even just one estimated physiological parameter being closer to the true value are visibly more likely to have higher accuracy; this is regardless of whether they originated from the less or more ‘noisy’ part of the experiment.
is the maximum f value obtained within this set. There are three pertinent things to note: (1) As the parameters become increasingly noisy, accuracy tends to drop, but there are still occasions which produce good results. (2) The ‘default’ parameter set is not necessarily the best one; but it’s difficult to predict a priori which one is. (3) Sets with even just one estimated physiological parameter being closer to the true value are visibly more likely to have higher accuracy; this is regardless of whether they originated from the less or more ‘noisy’ part of the experiment.If we had the theoretical ability to explore all the possible values and combinations for each of the algorithm’s parameters, we would obtain a set of segmentation results, covering all possible segmentation outcomes that are possible for a particular algorithm on a given image. We refer to this finite set, as the algorithm’s Segmentation Space. Equivalently, the complete Parameter Space is the set consisting of all possible parameter sets, each mapping to a segmentation in the segmentation space.
While exploration of the full parameter space is generally infeasible, we can select samples from a focused region, which is most likely to correspond to more accurate segmentations. If we treat a set of N parameters as an N-dimensional vector, then a simple way of doing this is by selecting samples with an N-dimensional gaussian probability function centered at a point of interest. A reasonable choice for this would be the default parameter set/vector suggested by the algorithm itself. This hopefully should restrict the segmentation space to a subset of generally more accurate segmentations, which we could then fuse to obtain a fuzzy segmentation.
It follows from Premise 1, that if we introduce a bias in the fusion process, to favour segmentations that are ‘better’, the fused result should logically be biased towards a ‘better’ fused result.
Premise 2: In the presence of a segmentation subspace, biasing segmentation fusion towards results associated with better physiological parameters, should result in a better fused result overall, compared to an unbiased fusion
The practical implication of applying the above insights to any algorithm, is that we shift the focus from having to optimise highly unintuitive parameters intrinsic to the segmentation algorithm, to something that is more intuitive within the context of the task at hand – i.e. the physiological parameters – and which is therefore easier, and more relevant to non image-analysis specialists.
4 Methods
The Segment cardiac segmentation suite by Heiberg et al. (http://segment.heiberg.se) [4] was used to obtain left ventricle (LV) segmentations from a set of images, kindly provided by the University of Oxford Centre for Clinical Magnetic Resonance Research at the John Radcliffe Hospital, Oxford. This set was produced on a 3.0T Siemens Tim Trio whole-body MRI scanner using a 4D (i.e. 3D+time) TrueFISP cineMRI protocol, from a patient undergoing a post-PCA investigation, following a diagnosis of an Inferior MI; the set was anonymised appropriately and no other clinical or radiological details were available. The image set consisted of 25 timeframes of 8 Short-Axis (SA) slices at a resolution of 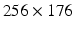 voxels, of size
voxels, of size 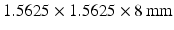 . Manual segmentations of the left ventricle were provided by an expert clinician, which were used as a gold standard; this was obtained as per-slice 2D contours, drawn at
. Manual segmentations of the left ventricle were provided by an expert clinician, which were used as a gold standard; this was obtained as per-slice 2D contours, drawn at 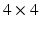 subresolution accuracy per in-slice image voxel, using the CMR42 cardiac imaging suite [5]. Full diastole was identified in timeframe 1, and full systole at timeframe 10. Data was processed using Matlab [6]; images were extracted from the DICOM files using a modified version of Laszlo Balkay’s DICOM reader [7]; all other processing (including extraction of contours from CMR42 files) is the work of the authors.
subresolution accuracy per in-slice image voxel, using the CMR42 cardiac imaging suite [5]. Full diastole was identified in timeframe 1, and full systole at timeframe 10. Data was processed using Matlab [6]; images were extracted from the DICOM files using a modified version of Laszlo Balkay’s DICOM reader [7]; all other processing (including extraction of contours from CMR42 files) is the work of the authors.
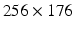 voxels, of size
voxels, of size 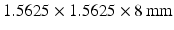 . Manual segmentations of the left ventricle were provided by an expert clinician, which were used as a gold standard; this was obtained as per-slice 2D contours, drawn at
. Manual segmentations of the left ventricle were provided by an expert clinician, which were used as a gold standard; this was obtained as per-slice 2D contours, drawn at  subresolution accuracy per in-slice image voxel, using the CMR42 cardiac imaging suite [5]. Full diastole was identified in timeframe 1, and full systole at timeframe 10. Data was processed using Matlab [6]; images were extracted from the DICOM files using a modified version of Laszlo Balkay’s DICOM reader [7]; all other processing (including extraction of contours from CMR42 files) is the work of the authors.
subresolution accuracy per in-slice image voxel, using the CMR42 cardiac imaging suite [5]. Full diastole was identified in timeframe 1, and full systole at timeframe 10. Data was processed using Matlab [6]; images were extracted from the DICOM files using a modified version of Laszlo Balkay’s DICOM reader [7]; all other processing (including extraction of contours from CMR42 files) is the work of the authors.A set of 100 segmentations was obtained by applying normally distributed random noise of linearly increasing standard deviation, on each of the default parameters (i.e. force modifiers; see Fig. 1) provided by Segment for the case of SSFP MRI; the noise was generated with mean 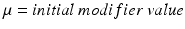 for each parameter, and standard deviation
for each parameter, and standard deviation  taking values linearly from 0 to
taking values linearly from 0 to 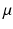 over the 100 experiments. Experiment 70, which was the best outcome in this set was retained as a reference to the best segmentation obtainable with this algorithm for this particular image. For each of the resulting segmentations, the following physiological parameters were derived:
over the 100 experiments. Experiment 70, which was the best outcome in this set was retained as a reference to the best segmentation obtainable with this algorithm for this particular image. For each of the resulting segmentations, the following physiological parameters were derived:
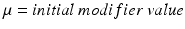 for each parameter, and standard deviation
for each parameter, and standard deviation 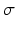 taking values linearly from 0 to
taking values linearly from 0 to 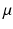 over the 100 experiments. Experiment 70, which was the best outcome in this set was retained as a reference to the best segmentation obtainable with this algorithm for this particular image. For each of the resulting segmentations, the following physiological parameters were derived:
over the 100 experiments. Experiment 70, which was the best outcome in this set was retained as a reference to the best segmentation obtainable with this algorithm for this particular image. For each of the resulting segmentations, the following physiological parameters were derived:
Volumes in systole (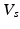 ) and diastole (
) and diastole (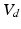 ), defined as the number of voxels in the set of LV-labeled voxels in systole (
), defined as the number of voxels in the set of LV-labeled voxels in systole (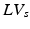 ) and diastole (
) and diastole (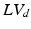 ) respectively
) respectively
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



