to simpler metrics that can be directly derived from imaging modalities such as 3D echo (wall thickness and cavity volume) or cine MRI (apicobasal distance).
The evaluated geometry based CFs are the 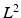 error norm of displacements (
error norm of displacements (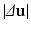 ) [22], a metric which expresses the average error in the displacements (
) [22], a metric which expresses the average error in the displacements (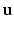 ) between data (
) between data (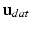 ) and simulations (
) and simulations (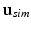 ):
):
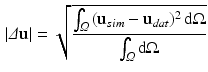
and the absolute differences between the data and the simulation in cavity volume, wall thickness (averaged over equatorial mesh nodes) and apico-basal distance (averaged over endo- or epicardial nodes of the base and the apex).
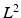 error norm of displacements (
error norm of displacements (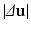 ) [22], a metric which expresses the average error in the displacements (
) [22], a metric which expresses the average error in the displacements (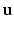 ) between data (
) between data (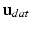 ) and simulations (
) and simulations (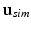 ):
):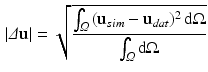
(1)
Energy Based Metric. The main contribution of this study is the introduction of a novel, energy based CF. This CF is based on the principle of energy conservation, which under the assumption of quasistatic loading and purely elastic behaviour [1, 4, 20], can be expressed as the external work being stored as elastic strain energy inside a deformable body (Eq. 2). Previous work has demonstrated the need to account for residual active tension (AT) in diastole [2, 20]. But focusing on the late diastolic window the residual AT can be assumed to be zero and its contribution to the work estimation negligible. Expressing the energy conservation (Eq. 2) over any two late diastolic frames, denoted as diastolic frame 1 ( ) and diastolic frame 2 (
) and diastolic frame 2 ( ) (and stating that the ratio of the external work at these two frames should equal the ratio of the elastic energy at the same frames) the energy based functional f is formulated (Eq. 3), where V is the domain of the undeformed (reference) configuration and
) (and stating that the ratio of the external work at these two frames should equal the ratio of the elastic energy at the same frames) the energy based functional f is formulated (Eq. 3), where V is the domain of the undeformed (reference) configuration and 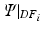 and
and 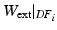 denote the strain energy density function and the external work respectively at the diastolic frame
denote the strain energy density function and the external work respectively at the diastolic frame 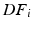 (
(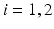 ).
).
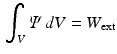
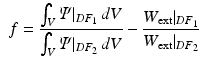
The elastic energy estimation relies on calculating the Green-Lagrange strains derived from the data as a result of the deformation field between the reference and the deformed geometries at a given frame (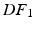 or
or 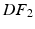 ).
).
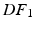 ) and diastolic frame 2 (
) and diastolic frame 2 (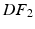 ) (and stating that the ratio of the external work at these two frames should equal the ratio of the elastic energy at the same frames) the energy based functional f is formulated (Eq. 3), where V is the domain of the undeformed (reference) configuration and
) (and stating that the ratio of the external work at these two frames should equal the ratio of the elastic energy at the same frames) the energy based functional f is formulated (Eq. 3), where V is the domain of the undeformed (reference) configuration and 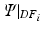 and
and 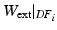 denote the strain energy density function and the external work respectively at the diastolic frame
denote the strain energy density function and the external work respectively at the diastolic frame 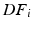 (
(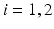 ).
).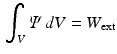
(2)
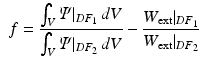
(3)
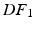 or
or 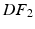 ).
).The external work is estimated as the work performed from the LV cavity pressure to increase the volume of the LV chamber. It should be noted that, unlike the geometry based CFs, which rely on the comparison of a geometric quantity between the data and the model simulation, the energy based CF is entirely data driven (see Fig. 1).
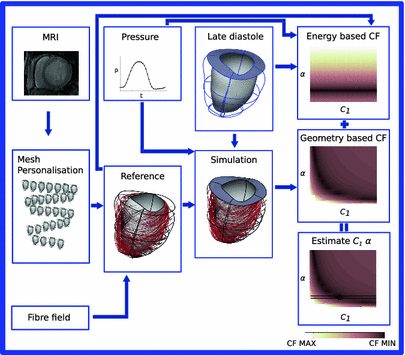

Fig. 1.
Summary of the followed pipeline, from FE model generation to CF evaluation and paramter estimation.
2.2 Diastolic Mechanical Model of the LV
To evaluate the performance of the CFs a model of the left ventricle (LV) in late diastole using clinical data is constructed, where diastolic behaviour is simulated as passive inflation under hydrostatic pressure.
Clinical Data. The clinical data used in this study consist of LV cavity pressure recordings used for the loading BCs and images from cine MRI for the deformation field and mechanical reference configuration in the model. The data were acquired from 2 Cardiac Resyncronisation Therapy (CRT) patients according to the clinical protocols followed for CRT patients in St. Thomas’ Hospital, London and one healthy volunteer. Imaging data consist of 2-D cine MRI stacks with ECG gating. The pressure data are derived from pressure catheterisation procedure before pacing protocols begin.
Mesh Personalisation. Finite element (FE) meshes of the LV geometry at each frame were created using an automatic pipeline combining mesh personalisation [8] and image registration [13] techniques. The mesh personalisation requires solely a binary mask representing the LV domain as input, and performs an automatic fitting of an idealised template mesh to the anatomy of the patient [8]. This technique is robust to the sparse resolution of cine sequences, and therefore the myocardial domain was defined by the manual segmentation of the end diastolic (ED) frame of each sequence. A temporal sparse free form registration technique extracts the warping field from the same sequence [13]. This field, that is continuous in time and space, is then fitted to the domain of the ED mesh using a variational technique [7], obtaining the sequence of meshes. Finally, a postprocessing step improves mesh quality and simulation stability [8, 9]. As in previous studies [20, 21], a relatively coarse mesh is chosen (12 elements and 1308 degrees of freedom with cubic Lagrange interpolation for the displacement field and linear for the pressure), in order to reduce the computational cost of simulations and regularise the deformation field from clinical data.
Myocardial Material Description. In this study the myocardium was modelled as a homogeneous, transversely isotropic material. The reason for choosing a transversely isotropic over an orthotropic material behaviour was two-fold: firstly, transvesely isotropic material laws utilise fewer material parameters and are thus more tractable within a parameter estimation framework (as opposed to more complex orthotropic material laws [5]). Secondly, this choice provides the opportunity to use a very popular transversely isotropic material law proposed by Guccione [3]. For the purpose of this study, the reformulated version of this equation (as proposed by [20]) will be adopted, since it helps illustrate the major direction of parameter coupling (between parameters 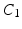 and
and 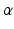 ), describing the stored elastic energy density
), describing the stored elastic energy density 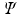 in each material point of the myocardium as:
in each material point of the myocardium as:
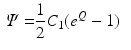
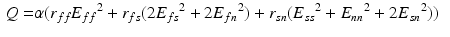
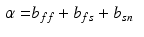
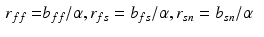
where 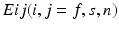 are the Green-Lagrange strain tensor components in fiber coordinates [12]. The parameter ratios (
are the Green-Lagrange strain tensor components in fiber coordinates [12]. The parameter ratios (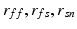 ) are assumed constant throughout this study and were assigned values that correspond to the average reported values in the literature.
) are assumed constant throughout this study and were assigned values that correspond to the average reported values in the literature.
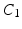 and
and 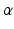 ), describing the stored elastic energy density
), describing the stored elastic energy density 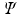 in each material point of the myocardium as:
in each material point of the myocardium as: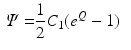
(4)
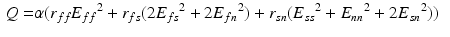
(5)
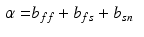
(6)
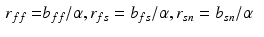
(7)
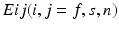 are the Green-Lagrange strain tensor components in fiber coordinates [12]. The parameter ratios (
are the Green-Lagrange strain tensor components in fiber coordinates [12]. The parameter ratios (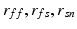 ) are assumed constant throughout this study and were assigned values that correspond to the average reported values in the literature.
) are assumed constant throughout this study and were assigned values that correspond to the average reported values in the literature.FE Model of the Reference Configuration. The finite strain framework employed in cardiac mechanics involves the use of a reference and a deformed state configuration. The reference configuration represents an idealised geometry where the domain is unloaded and there are zero stresses and strains. However, finding this idealised geometry in practice is an elusive task which is associated with many uncertainties. In this work this problem is circumvented by considering only geometries available in the clinical data as possible reference frame candidates. More specifically after examining several possible reference states the early-diastolic frame with the minimum volume was chosen as the reference configuration in all cases. The FE model of the LV is completed with the fitting of a standard fiber field [15] to the reference frame mesh (Fig. 1).
Mechanical Simulations. For the estimation of the geometry based CFs mechanical simulations were performed with parameter sweeps of 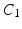 and
and 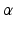 parameters. These involve the passive inflation of the LV reference geometry to ED pressure with prescribed ED basal nodes displacements using the CHeart 2 nonlinear FE solver.
parameters. These involve the passive inflation of the LV reference geometry to ED pressure with prescribed ED basal nodes displacements using the CHeart 2 nonlinear FE solver.
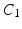 and
and 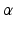 parameters. These involve the passive inflation of the LV reference geometry to ED pressure with prescribed ED basal nodes displacements using the CHeart 2 nonlinear FE solver.
parameters. These involve the passive inflation of the LV reference geometry to ED pressure with prescribed ED basal nodes displacements using the CHeart 2 nonlinear FE solver.The meshes and simulation outputs were visualised with cmGui 3.
3 Results
3.1 Geometry Based Metrics
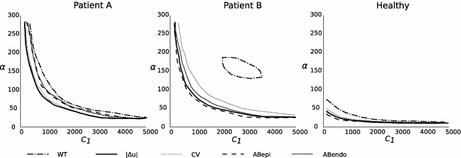
The parameter combinations that minimise the geometry based CFs are shown in Fig. 2, where it can be observed that they represent similar regions in the parameter space. Therefore these metrics can not improve the identifiability of the stiffness model. The exception to this observation is the landscape of the wall thickness CF in Patient case B, which demonstates the inability of this simpler metric to provide a reliable CF.