Susceptibility Contrast in Tissues: Gradient Echoes versus Spin Echoes

Jerrold L. Boxerman

Matthias J.P. van Osch

Kathleen M. Schmainda

Introduction

This chapter summarizes susceptibility-based magnetic resonance imaging (MRI) contrast and the differential effects of gradient-echo (GE) and spin-echo (SE) MRI pulse sequences on this contrast. The principles of susceptibility contrast¹ provide the link between the conventional use of injectable tracers (tracer kinetic theory)² and dynamic susceptibility contrast MRI (DSC-MRI),³ which uses exogenous contrast agents to quantify cerebral hemodynamics in the setting of stroke⁴^,⁵^,⁶ and neoplasms.⁷^,⁸^,⁹ Susceptibility contrast is also the fundamental contrast mechanism behind functional brain activation studies using endogenous contrast provided by deoxyhemoglobin.¹⁰ Following bolus contrast agent injection, tracer kinetic analysis of contrast concentration-time data yields hemodynamic information about blood flow and blood volume.¹¹ To measure cerebral blood volume (CBV) or cerebral blood flow (CBF) with DSC-MRI, changes in signal intensity versus time first must be converted into tissue contrast agent concentration-time curves.³ It is both a potential strength and a possible limitation that the relationship between MR signal intensity, contrast agent concentration, and other physiologic (vascular volume fraction, blood vessel size, proton diffusion rate in tissue) and experimental (MR pulse sequence parameters, magnetic field strength) variables is more complex and inexact than the relationships for iodinated computed tomography (CT) contrast material discussed in Chapter 9.

This chapter will review the interplay between blood vessel (compartment or magnetic field perturber) size, contrast agent concentration, and pulse sequence parameters on MR signal (more specifically, changes in T₂ relaxivity), focusing on GE versus SE acquisitions. The fundamental difference in the vessel size dependence of GE and SE relaxivity will be discussed. Whereas GE relaxivity increases with increasing vessel size but plateaus above a vessel size typically on the size scale of capillaries, SE relaxivity peaks around typical microvessel sizes and then monotonically decreases with increasing vessel caliber. Several fundamental implications of this phenomenon with regard to imaging cerebral hemodynamics using DSC-MRI are discussed. These include the linearity of relaxivity versus contrast agent concentration, which is required for accurate estimates of CBV and CBF using tracer kinetic theory; the differential dependence of GE and SE relaxivity on the proton diffusion rate in tissue, which may affect the accuracy of perfusion estimates in the setting of acute stroke and cellular neoplasms; and the ability to assess average intravoxel microvessel size in vivo, with particular applications to imaging angiogenesis and the diagnosis and posttreatment monitoring of brain neoplasms.

Fundamentals of Magnetic Susceptibility

Magnetic susceptibility phenomena can affect MR images both macroscopically, leading to typical image artifacts associated with poor magnet shimming, metallic implants, and susceptibility differences at air–tissue interfaces, and microscopically, which can be exploited by dynamic imaging with contrast agents to quantify tissue hemodynamics and measure various physiologic parameters. The response of a material’s internal magnetization to an applied external magnetic field is referred to as its magnetic susceptibility.¹²

Diamagnetic materials (most organic and many inorganic compounds containing low-molecular-weight elements such as carbon and hydrogen with paired electrons) reduce the magnitude of an applied external field analogous to Lenz’s law by inducing an opposing magnetic field. Diamagnetism accounts for MRI artifacts typically seen at air–tissue boundaries.¹³ Transition metal ions (like the ferrous [divalent] and ferric [trivalent] oxidation states of iron, gadolinium, and dysprosium) have unpaired orbital electrons that align parallel or antiparallel to an applied magnetic field, producing a net magnetization. Because more dipoles align parallel to the field than antiparallel, the applied field is enhanced, and materials that enhance the magnitude of the external field in this manner are said to be paramagnetic.¹⁴^,¹⁵ For both diamagnetic and paramagnetic materials, the induced magnetization, M, is proportional to the applied magnetic field, B₀: M = χB₀,¹²
where χ is the material’s magnetic susceptibility and is positive for paramagnetic materials and negative for diamagnetic materials. The induced magnetization M for paramagnetic materials yields an effective magnetic field B_eff = B₀ + χB₀ = B₀ + ΔB that exceeds the applied field (χ > 0), causing local protons to precess with angular frequencies ω_eff = γB_eff greater than ω₀ = γB₀, where γ is the gyromagnetic ratio (see Chapter 4).¹⁶ More details on paramagnetism and diamagnetism can be found in Chapter 6.

Heterogeneous distributions of magnetic susceptibility within a voxel therefore cause microscopic perturbations of proton resonance frequencies by modifying the magnetic field sensed by local spins. Instead of all intravoxel protons precessing at ω₀, a range of precessional frequencies will exist owing to spatially variant B_eff resulting from magnetic susceptibility heterogeneity that causes more rapid signal decays as reflected by a shorter T₂^* decay time. In the setting of DSC-MRI, the magnetic susceptibility heterogeneity is due to paramagnetic contrast material (e.g., Gd-DTPA) within a microvascular network. This dephasing attenuates the MR signal (see Geek Box 1).

In the absence of proton diffusion, there is no MR signal loss or phase distortion for pulse sequences that completely refocus static inhomogeneities (SE). The MR signal decreases, though, for pulse sequences that do not completely refocus static inhomogeneities, such as GE and asymmetric SE acquisitions. Protons that diffuse through magnetic field variations arising from heterogeneous magnetic susceptibility distributions, however, will accrue nonstatic phase inhomogeneities, which when averaged over all spins within a voxel yield MR signal loss. The signal loss from this “dynamic dephasing” occurs not only for GE but also for SE acquisitions that completely refocus static inhomogeneities (see Chapters 4 and 6). It is this signal loss during transient passage of exogenous paramagnetic contrast agent that provides the analog between DSC-MRI and conventional tracer kinetics, and a detailed understanding of the DSC-MRI contrast mechanism is important for correct application of classical indicator dilution theory.¹¹

Geek Box 1

ΔR₂ is defined as the change in relaxation rate, Δ1/T₂:

where T_2pre and T_2post are the tissue T₂ relaxation times in the absence and presence, respectively, of susceptibility-induced field perturbations (see Chapter 6). S is the signal attenuation due to susceptibility-induced phase dispersion and can be expressed as an expectation value of proton phases:

taken over all paths through the medium for each initial proton position, where p(φ(t), r^→) is the probability density function in which a proton starting at position r^→ acquires phase φ by time t. As phase distributions φ(t) become more heterogeneous and “spread apart,” S(t) decreases, representing the typical transient signal loss during DSC-MRI. The last integration is a Fourier transform and in case p is Gaussian, it can be shown that the summation over the entire spin ensemble in the voxel yields signal attenuation, similar to diffusion weighting.

Note that with regard to diffusion weighting, it does not matter whether diffusion weighting is achieved by energizing large external magnetic field gradient coils or by “turning on” microscopic intravoxel local field gradients via a susceptibility contrast agent or the blood oxygenation level–dependent (BOLD) effect. Both are manifestations of diffusion weighting, and in fact the microgradients achieved by the contrast agent are comparable to the gradients achieved by external gradients.

Two fundamental assumptions are required for DSC-MRI to accurately calculate the concentration of contrast agent from dynamic T₂– or T₂^*-weighted images and mimic classical tracer kinetics:

A linear (or known) relationship exists between measured relaxivity and contrast agent concentration (magnetic susceptibility difference Δχ) so that the MR signal (changes) can be associated with tracer concentration (changes).
The contrast agent remains intravascular (volume of distribution is limited to the vascular volume fraction) with a negligible effect on the MR signal from leakage-induced T₁ changes.

Violation of these assumptions would lead to an erroneous measurement of the tissue concentration-time curve and a consequent miscalculation of hemodynamic parameters. Because of the requirement for intravascular distribution of contrast agent, DSC-MRI has been applied traditionally to the brain, where the blood–brain barrier limits contrast agent extravasation under normal circumstances. This chapter considers issues related to the first assumption; Chapter 28 addresses issues related to contrast agent leakage in the setting of disrupted blood–brain barriers as might be seen with high-grade neoplasms and subacute infarcts.

Unlike x-ray-attenuating iodinated contrast agents (CT), DSC-MRI contrast agents are not imaged directly (see Chapter 6 and 7). Rather, compartmentalization of paramagnetic contrast agents (such as gadolinium chelates, Gd-DTPA) with large magnetic moments within the vasculature induces long-range magnetic field perturbations that augment local magnetic field inhomogeneities, thereby
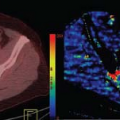
enhancing dephasing of protons in the vicinity of these tracers and transiently shortening the transverse relaxation time, T₂ and T₂^*.¹^,³ Figure 11.1 summarizes this effect in tissue, where intravascular paramagnetic contrast agent magnetizes the microvessels, creating locally variant magnetic field perturbations that depend on contrast agent concentration (susceptibility difference Δχ), vessel size, and vessel geometries. Protons lose phase coherence as they diffuse through the magnetic field perturbations and “sense” different magnetic field distributions than other intravoxel protons, yielding heterogeneous proton phase distributions and overall MR signal attenuation.¹⁷ The change in transverse relaxation rate is often described in terms of relaxivity, ΔR₂ (see Chapter 6 and Geek Box 1), which depends on the field strength, size and geometry of the confining vessels, vascular volume fraction, susceptibility difference between agent and surrounding tissue, proton diffusion rate (i.e., the underlying apparent diffusion coefficient [ADC] of the tissue), and specific pulse sequence parameters (e.g., echo time). Elucidation of this complex relationship was historically approached with analytical techniques for limiting cases where proton motion was either very fast or very slow or magnetic perturbers (vessel sizes) were either very large or very small.

FIGURE 11.1. Diagram of the fundamental susceptibility contrast mechanism. An intravascular paramagnetic contrast agent magnetizes the microvessels, creating locally variant magnetic field perturbations that depend on contrast agent concentration (susceptibility difference Δχ), vessel size, and vessel geometries. Protons lose phase coherence as they diffuse through the magnetic field perturbations and “sense” different magnetic field distributions than other intravoxel protons, yielding heterogeneous proton phase distributions and overall magnetic resonance signal attenuation.

Geek Box 2

These regimes are most naturally defined in terms of the diffusive correlation time of protons with respect to the magnetic field inhomogeneities, τ_D, and the characteristic variation in Larmor frequency due to field perturbations, δω.²⁵^,⁶² For localized magnetic field perturbers, τ_D is the time required for diffusion past the perturber, and δω is the change in frequency at the surface of the perturber, and these quantities can be approximated as τ_D = R²/D and δω = γB_eq(R), where R is the radius of the perturber, B_eq(R) is the magnetic field on the surface of the perturber, and D is the diffusion coefficient.²⁵^,⁶² Because B_eq is influenced by the magnetic susceptibility of the perturber, Δχ, which in turn is a function of contrast agent concentration in the case of the vasculature and DSC-MRI, δω is proportional to contrast agent concentration.

Models of Susceptibility Contrast

Loss of transverse magnetization with magnetic field inhomogeneities is classically separated into three regimes, historically termed the motionally narrowed, intermediate, and linear gradient, which are determined by the magnetic, geometric, and dynamic properties of the system (Fig. 11.2 and Geek Box 2). Note that some investigators have referred to the linear gradient regime also as the static dephasing regime. These three regimes are essentially determined by the relationship of the rate at which protons diffuse and the size scale and strength of the magnetic field perturbers, which specifically are contrast-filled blood vessels in the setting of DSC-MRI.

FIGURE 11.2. Diagram of the analytical regimes of susceptibility contrast, which are determined by the relationship of the rate at which protons diffuse and the size scale and strength of the contrast-filled blood vessels (magnetic field perturbers). For fast diffusion or small perturbers (motionally narrowed), all protons sense equivalent field distributions, yielding very small relaxivity change for both gradient echo (GE) and spin echo (SE). For slow diffusion or large perturbers (linear gradient), magnetic field inhomogeneities are corrected with SE yielding very small relaxivity change, but maximal for GE.

Motionally Narrowed Regime

When the proton diffusion rate, 1/τ_D, is much greater than the size scale of vessels, R, or the frequency changes,
δω, induced by proton diffusion along the susceptibility gradients, diffusion is fast with respect to the spatial variations of the magnetic field perturbations and the system is said to be in the motionally narrowed regime. In the motionally narrowed regime, the size and time scales are such that all protons effectively experience identical magnetic field profiles because they each diffuse past many different perturbers during the time period of interest, and can be considered to be in “fast exchange.” The assumptions of this model are likely to be met in cases where the size of the magnetic field perturbers is small or water diffusion rates are high. In this regime, both gradient-echo and spin-echo relaxivity can be shown to vary quadratically with δω, implying a superlinear dependence of relaxivity on contrast agent concentration (see Geek Boxes 2 and 3).

Linear Gradient or Static Dephasing Regime

At the other extreme, where diffusion rates are slow, or the magnetized vessel or peak field perturbations are very large, there exists a slow exchange limit called the linear gradient or static dephasing regime, where δω · τ_D >> 1, and field perturbations are adequately modeled by local, uniform gradients.¹⁸ At the linear gradient regime, protons only sample a small region of the heterogeneous magnetic field distribution, which at this length scale can be approximated to be linear, and relaxation can be described in terms of an ensemble of spins moving through a static distribution of uniform gradients. Protons experience an essentially static field. SE T₂ relaxation is not enhanced because of refocusing and the very limited phase accrual in this regime, but enhanced GE T₂^* relaxation occurs owing to loss of phase coherence within the voxel (see Geek Box 4).

Geek Box 3

Under motionally narrowed conditions, the relaxation rate resulting from a spherical perturber may be expressed as ΔR₂ = 16τ_D·f_v·(δω)²/135, which varies quadratically with magnetic field and susceptibility difference, δω, and inversely with D (1/τ_D).⁶² This relationship suggests that transverse relaxivity increases as the square of contrast agent concentration in the motionally narrowed regime because δω is proportional B_eq, which is proportional to Δχ and contrast agent concentration. For a constant volume (f_v) of perturbers, a smaller number of larger particles yields more relaxation enhancement than a greater number of smaller particles, and hence the nature of the spatial distribution of a fixed quantity of magnetic material markedly influences relaxivity change.

Geek Box 4

Under linear gradient conditions, an approximation for T₂ relaxivity is ΔR₂ = (γ · σ_G · TE)² · D/12, where σ_G² denotes the variance of the internal gradient distribution induced by the perturbation.¹⁸ This predicts a linear dependence of relaxivity on diffusion coefficient (as opposed to inverse linear dependence for the motionally narrowed regime) and inverse quadratic dependence on perturber size because τ_D ∼ R²/D. It should be noted that the aforementioned expression for ΔR₂ is also the expression for the diffusion attenuation for a constant-gradient diffusion-weighted experiment. Strictly speaking, the change in R₂ caused by a contrast agent is not so much due to spin–spin interaction but due to diffusion weighting. (Spin-echo imaging with a susceptibility agent on board is therefore in essence a diffusion-weighted imaging experiment in disguise with endogenous diffusion gradients on board.)

By contrast, an analytical expression for ΔR₂^* in the linear gradient regime is ΔR₂^* = 2π/3√3f_v · δω,⁶³ with ΔR₂^* being independent of diffusion in this regime but increasing linearly with δω and contrast agent concentration.

The qualitative features of the size dependence of SE and GE relaxivity change can thus be summarized. The abscissa essentially scales as correlation time τ_D = R²/D, where R is the vessel or compartment size and D is the diffusion coefficient. For long correlation times, that is, for either large vessel sizes or slow diffusion, SE relaxivity approaches zero because each proton travels in an essentially uniform field and the phase of each proton is perfectly refocused by the π-pulse. Because relaxation depends on the square of the magnetic field gradient,¹⁹ which varies inversely with perturber size (i.e., large perturbers generate small gradients), SE relaxivity decreases dramatically with increasing perturber size. GE relaxivity is maximum under such circumstances, however, because the variance of the static field is not smoothed to any extent by proton motion. In this regime, ΔR₂^* is interpreted as nearly pure gradient dephasing, independent of the diffusion of the proton spins. For short correlation times (small vessel sizes or fast diffusion), SE and GE relaxivity both approach zero, because the phase distributions are motionally narrowed as each proton is experiencing an essentially identical field distribution. When δω · τ_D is on the order of unity, which is applicable in vivo,¹⁸ peak SE relaxivity is realized. This occurs because proton motion is great enough (or perturber size is small enough) to disrupt the constant field environment created by long τ_D, without completely narrowing the phase distribution, and hence a significant phase distribution remains even after refocusing.

Applicability of analytical expressions for behavior in the motionally narrowed and linear gradient regimes to
susceptibility contrast in vivo is limited, however. The physiologic sizes and time scales inherent to in vivo susceptibility contrast due to compartmentalized intravascular contrast agent (Gd-DTPA) often fall between these two extreme limits (see Geek Box 5). Quantitative assessment of relaxivity in this intermediate regime is inaccessible with analytical techniques and has best been elucidated with numerical methods, such as Monte Carlo techniques that estimate relaxivity by accumulating the phase from the stochastic walk of many protons through a simulated microvascular environment.¹⁷^,²⁰^,²¹

Geek Box 5

For a capillary with radius R ≈ 3 μm⁶⁴ and diffusion constant D ≈ 1 × 10⁻⁵ cm²/s⁻¹,⁶⁵ τ_D = R²/D ≈ 9 msec. For an applied field strength of B_o = 1.5–3T and a variation in susceptibility Δχ ≈ 1 ppm between the contrast agent–filled capillary space and the extravascular tissue (typical for Gd-based contrast agents), δω τ_D ∼ γΔχB₀τ_D ∼ 10⁰ − 10¹, and so it is clearly not the case that δω τ_D >> 1 or δω τ_D ≪ 1. Qualitatively, when δω τ_D is intermediate (on the order of unity), the static field variance is no longer the only important parameter, because the field seen by moving spins is essentially smoothed and the phase variance decreases.

Monte Carlo Calculations

Monte Carlo simulations of proton “random walks” have been used to estimate transverse relaxation enhancement caused by diffusion through inhomogeneous magnetic fields and typically assume specific perturber geometry for representing the microvessel architecture of the tissue being studied. Specific perturber geometries that have been studied with Monte Carlo techniques include a single cylinder,²² multiple cylinders,²⁰^,²³ regular grid-like arrays of cylinders,²⁴ randomly distributed spherical perturbers,¹⁷^,²⁵ and ensembles of randomly oriented cylinders.²¹ These Monte Carlo simulations have provided invaluable insights into susceptibility contrast mechanisms. Briefly, this technique simulates the proton diffusion through voxels containing vessels filled with contrast agent and determines the MR signal loss due to changes in transverse relaxivity (see Geek Box 6).

Only gold members can continue reading. Log In or Register to continue