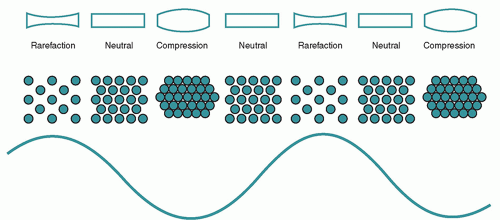
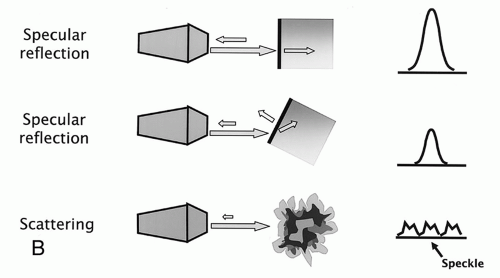
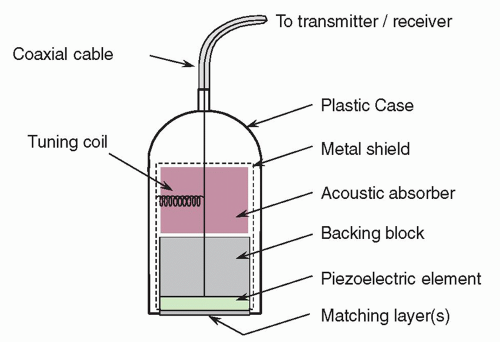
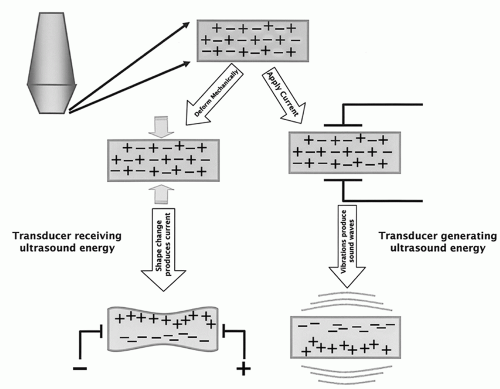
Sound waves are a form of mechanical energy that propagates through an elastic medium via pressure disturbances. This leads to compression and rarefaction of the particles that compose it. Pressure changes are created by forces acting on the molecules within the medium. A simple model to illustrate this is a spring (
Figure 7.1). Mechanical deformation induced by an external force (eg, plane piston) causes compression, which leads to an increase in pressure of the medium, and subsequently rarefaction. The force is reversed by the backward motion of the piston, which causes the compressed particles to transfer their energy to adjacent particles, ultimately leading to a reduction in the local pressure amplitude (rarefaction). The compression continues to travel forward while the section of spring contacting the piston becomes stretched. A series of longitudinal compressions and rarefactions propagate through the medium with the continued back-and-forth motion of the piston. The vibrations of longitudinal waves occur along their travel direction, whereas those of transverse waves are perpendicular to the travel direction.
An additional method of producing acoustic energy involves short bursts, which equate to a small pulse traveling through a medium by itself. Reflections of the incident energy pulse result from differences in the elastic properties of the medium. Multiple pulses of ultrasound that are reflected back to the receiver from the tissue interfaces form the image. The pulse emitted by a transducer is approximately 1 ms or less. As the pulse propagates through the tissue, signals are reflected back to the transducer. A formula relates the depth at which the returning echo signal is formed with the time delay between the pulse emission and echo reception:
Amplitude, wavelength, frequency, and velocity
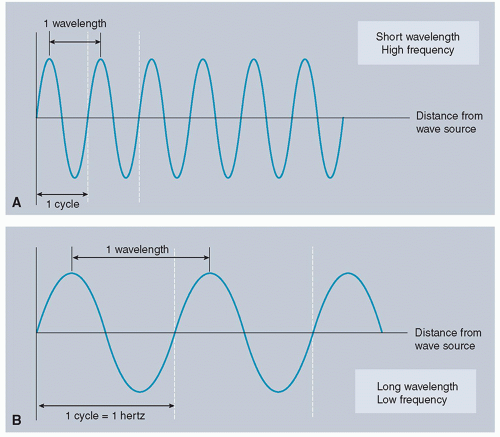
The amplitude of a sound wave equals the degree of pressure change from equilibrium. Larger amplitudes lead to denser compressions, which create sound with higher intensities. The wavelength (λ) of an ultrasound is the distance (in millimeter or micrometer) between compressions or rarefactions. Wavelength can also be measured between two repeating points on a sinusoidal wave of pressure amplitude (successive wave crests) (
Figure 7.2). Frequency (
f) is the number of times the wave oscillates during a cycle per second (sec). Frequency also refers to the number of wavelengths passing a specific point per second. The unit of measurement is in hertz (Hz), given that 1 Hz equals one oscillation per second. Sound waves with frequencies between 15 and 20 000 Hz (20 kHz) compose the audible acoustic spectrum. Sound waves with frequencies below 15 Hz are called infrasound, whereas those with frequencies above 20 kHz are called ultrasound. Medical ultrasound typically uses frequencies between 2 and 15 MHz (15 000 000 Hz); however, specialized applications can use frequencies as high as 50 MHz. The period of a sound wave represents the time duration of one wave cycle and is equal to 1/
f. The speed of sound, which is the distance traveled by the wave per unit of time, is equal to the wavelength divided by the period. Because period and frequency are inversely proportional (period = 1/
f), the relationship between velocity, wavelength, and frequency can be represented as
v = λf
where v is the velocity of sound (m/s), λ is the wavelength (m), and f is the frequency (cycles/s).
The velocity of sound depends on the medium in which the wave is propagating through, and this is highly variable between different materials. The speed of the wave depends on two factors—the bulk modulus (B) and the density (ρ) of the medium. The bulk modulus is a measurement of the stiffness of a medium and how well it resists compression. Relating speed of sound in a medium with bulk modulus and density can be represented as
where the SI units are as follows:
v (m/s),
B (kg/ms
2), and ρ (kg/m
3). A highly compressible medium (eg, air) has a low speed of sound, whereas a less compressible medium (eg, bone) has a higher speed of sound. The density and speed of sound for relevant materials in medical imaging are listed in
Table 7.1. The varying speeds of sound modulated at the boundaries of tissues provide the fundamental reason for contrast in ultrasound imaging.
Within a given tissue medium, ultrasound frequency is independent of changes in sound speed. Hence, the wavelength is determined by frequency and the propagation medium. Wavelength depends on the compressibility of the material the sound wave is propagating through. An ultrasound transducer with a frequency of 2 MHz will result in a wavelength of 0.77 mm in soft tissue, 0.17 in air, and 1.7 mm in bone.
Given that the speed of sound in soft tissue is approximately 1540 m/s (equal to 1.54 mm/µs), the wavelength (in mm) within soft tissues can be calculated as follows:
λ = v/f = 1.54 mm/µs/f (MHz) = 1.54 mm/10-6 s/f (106/s) = 1.54 mm/f (MHz)
The wavelength changes at the boundaries of two different media due to the change in sound speed.
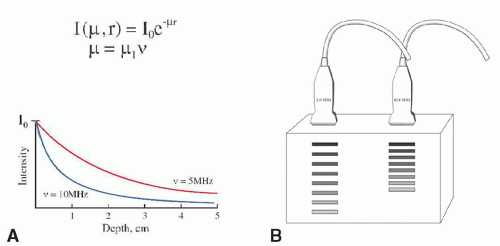
The wavelength and frequency determine the spatial resolution of the image and the attenuation of the ultrasound beam energy. An ultrasound beam with high frequency, and hence a small wavelength, provides superior resolution and image detail than does a low-frequency beam. However, a high-frequency beam is limited in the depth it can penetrate. Ultrasound beams with a low frequency provide lower resolution and image detail; however, they can penetrate to a much deeper depth. Consequently, the choice between using a higher or lower frequency ultrasound beam depends on the particular clinical application. Lower frequency waves (3.5-5 MHz) are used for thicker body parts (eg, abdominal imaging), whereas higher frequency waves (7.5-10 MHz) are used for smaller body parts or when the target is close to the skin (eg, thyroid, breast).
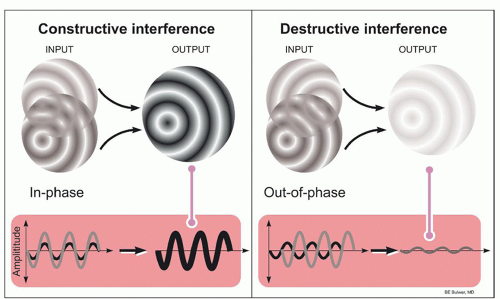
Ultrasound machines contain acoustic transmitters, which produce different independent sound beams. These unique beams can interact with one another, leading to constructive or destructive wave inference or complex interference patterns (
Figure 7.3). Interactions of two ultrasound waves that have the same frequency and phase result in a beam with increased amplitude (constructive interference). Interactions of two ultrasound waves that are 180° out of phase with one another result in an output wave with a lower amplitude (destructive interference). Interactions between ultrasound waves of slightly different frequencies result in waveforms of varying amplitudes (complex interference). The two most important factors determining the degree of interference include the phase of the sound wave and the amplitude of the interacting beams.
Pressure, intensity, and the dB scale
Acoustic energy causes displacement of particles and variations in local pressure as it propagates through a medium. The variations in pressure are referred to as pressure amplitude (
P). Pressure amplitude is equal to the difference between the peak maximum value or peak minimum value and the average pressure within a medium. The peak maximum (positive pressure amplitude) and the peak negative (negative pressure amplitude) values are equal when a symmetrical waveform is present. However, the compressional amplitude typically exceeds the rarefactional amplitude to a large degree in most diagnostic ultrasound applications. The SI unit of pressure is the pascal (Pa), which equals one newton per
square meter (N/m
2). Most diagnostic ultrasound beams deliver peak pressure levels of approximately 1 MPa (megapascal), which exceeds the earth’s atmospheric pressure 10-fold.
Power refers to energy per unit time. Intensity (I) is the amount of power per unit area. Intensity is proportional to the pressure amplitude squared (I ∝ P2). Therefore, doubling the pressure amplitude leads to a quadruple increase in intensity. The units of intensity in medical diagnostic ultrasound are milliwatts per centimeter square. Relative intensity is defined in units of the decibel (dB) and calculated using the following equation:
Relative intensity (dB) = 10 log (I2/I1)
Alternatively, relative pressure (also defined in units of dB) can be calculated as follows:
Relative pressure (dB) = 20 log (P2/P1)
In these equations, I1 and I2 refer to intensity levels and P1 and P2 refer to pressure amplitude values. The base 10 logarithm (“log”) is used to compress the large potential variance in intensity ratios between the incident pulse and the returning echoes. Every 10 unit change in the dB scale represents a change in intensity to the order of 10 times the magnitude, which means a 20 dB change equates to a change in 100 times the magnitude. An intensity value of 60 dB is equivalent to an incident intensity that is 106 (ie, 1 million) times that of the returning echo. The dB levels are positive when the incident ultrasound intensity is greater than that of the returning echo (ie, intensity ratio > 1). Alternatively, the dB levels are negative when the incident ultrasound intensity is less than that of the returning echo (ie, intensity ratio < 1). Furthermore, a decrease of 3 dB equals a 50% loss of signal intensity. The thickness of tissue required to reduce the intensity of the ultrasound by 3 dB is referred to as the half-value thickness (HVT).
Distance, area, and volume measurements
Measurements of distance, area, and volume during ultrasound examinations are possible because the speed of sound in soft tissues is nearly constant (1540 ± 15 m/s). Calibration of the instrument is readily determined depending on the round-trip time of the pulse and the echo. Careful selection of the reference points is necessary to ensure measurement accuracy. Selecting points along the direction of the ultrasound beam typically yields measurements more reliable than points measured in the lateral plane given the improved spatial resolution. Furthermore, measuring the distance between the leading edges of two objects lying in the axis of the beam is reliable because these points are less affected by variations in echo signal amplitude. The circumference of a circular object can be calculated using the measured radius (r) or diameter (d) with 2πr or πd. The area of an object or region of interest is calculated using distance measurement and by assuming a specific geometric shape. The area of a region of interest in a single image plane can be extended to 3D volume measurements by estimating the slice thickness (elevational resolution).