Vessel Size Imaging

Valerij G. Kiselev

Heiko H. Schmiedeskamp

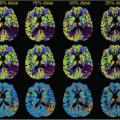
Vessel size imaging (VSI) is a magnetic resonance imaging (MRI) modality for evaluating the mean capillary caliber in the brain. This method is based on comparison of attenuation of gradient-echo (GE) and spin-echo (SE) signals in the presence of paramagnetic contrast confined to the blood pool. It has been shown that the dependencies of GE and SE amplitudes on the vessel size are qualitatively different, as illustrated in Figure 13.1.¹^,² To understand the selective sensitivity of different MRI pulse sequences, it is useful to discuss the basic principles of transverse relaxation in living tissue (see Chapter 6).

The interpretation of VSI measurement results relies on quantitative expressions for GE and SE relaxation rates. The presence of analytical equations is helpful in determining different approaches to VSI.

The most practically relevant implementations of VSI can be looked at as straightforward extensions of conventional dynamic susceptibility contrast (DSC) MRI and can be performed simultaneously with perfusion measurements. Pulse sequence requirements are discussed in this chapter.

Alternative approaches to measurement techniques and data interpretation are briefly reviewed in this chapter. Limitations and possible artifacts are also discussed. Similar to many other in vivo methods, the accuracy of VSI is difficult to verify, and this is also discussed in this chapter.

FIGURE 13.1. Relaxation rate in simulated tissue as a function of the radius ρ of a monosized vessel population for gradient-echo (GE) and spin-echo (SE) measurements. The points show the results of Monte Carlo simulations¹; with permeable vessel walls for small vessels (crosses) and impermeable walls for large ones (circles). The lines were obtained using interpolation formulae between the diffusion narrowing regime (DNR) and the static dephasing regime (SDR) similar to ref.² Simulation parameters were B₀ = 1.5 T, ζ = 2%, χ = 10⁻⁷, D = 1 μm²/ms, T_E = 60 ms for GE measurements and T_E = 100 ms for SE measurements.

Principles of Transverse Relaxation in Tissue

MR signal relaxation is caused by a randomly varying magnetic field experienced by nuclear spins, either in space or time. The underlying fundamental process is the microscopic molecular motion that results in a rapidly changing component of the total magnetic field (for more details see Chapters 6 and 11). This motion is very fast with a correlation time on the order of 10⁻¹² seconds. All molecules are affected by this motion and their relaxation behavior is similar, which is called homogeneous broadening or true relaxation. Note that any memory effect in the spin phase is lost for times longer than the correlation time, which means that the signal attenuation is not reversible using MRI refocusing pulses applied on the time scale of milliseconds.

The opposite situation is the constant macroscopic magnetic field varying in space as a consequence of imperfect shimming or magnetic field inhomogeneities induced by the difference in the magnetic susceptibility between air and tissue. Spins within a given voxel experience different magnetic field strengths and thus precess at different Larmor frequencies, leading to a loss of phase coherence. This is commonly referred to as inhomogeneous broadening or apparent relaxation. As each nuclear spin experiences a constant offset from the main magnetic field, the apparent relaxation can be removed by generating SE signals. The specific echo time does not matter, provided that it is shorter than the true relaxation time. This can be regarded as the perfect phase memory in the case of inhomogeneous broadening.

The above classification separating true and apparent relaxation works perfectly for solutions analyzed with nuclear magnetic resonance spectrometers. In contrast, biologic tissue has an additional mesoscopic scale, which is defined by the size of cells within tissue (Fig. 13.2). Some cells, such as deoxygenated erythrocytes, are paramagnetic. Furthermore, the presence of paramagnetic contrast agent (CA) in blood plasma can lead to magnetic susceptibility differences between different tissue compartments. These differences induce a magnetic field of complicated geometry on a spatial scale that is associated with the size of these compartments, which is typically on the order of or larger than 1 micrometer. Water diffusion results in constant displacement of individual water molecules. Remarkably, the displacement by diffusion is in the same order of magnitude as the length of
magnetic field variations (i.e., close to or larger than 1 micrometer) for the duration of an MR measurement with a typical echo time (T_E) in the range of tens of milliseconds. This means that both mechanisms discussed earlier occur simultaneously. Nevertheless, the TE of an applied MRI pulse sequence matters. In general, a dephasing process can be refocused if it is slow in comparison with TE, but it cannot be refocused if its correlation time is shorter than TE. In vivo MRI measurements often fall into an intermediate regime in which TE is on the same order of magnitude as the correlation time. As a consequence, the mesoscopic contribution to the transverse relaxation rate depends on the applied measurement technique (in particular on the parameter TE), time-dependent diffusion coefficient and the tissue microarchitecture in a complex way. Moreover, its dependence on the contrast agent concentration is generally nonlinear.

FIGURE 13.2. Different spatial scales that contribute to the transverse relaxation according to the scale of the magnetic field induced by heterogeneous magnetization. A single voxel imaged with MRI on the macroscopic scale (right) might be affected by a susceptibility-induced magnetic field at tissue–air interfaces. Such a voxel is composed of a microvascular network on the mesoscopic scale (center). This network can become paramagnetic after contrast agent injection, creating a magnetic field that changes on this scale. In turn, an individual contrast agent molecule affects water on the much finer microscopic scale (left).

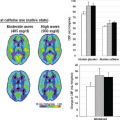
One might wonder whether this mesoscopic contribution is small in comparison with the microscopic and macroscopic contributions. An answer to this question can be found by considering the DSC MRI signal averaged across the thalamus of a patient during the passage of a CA through the brain, as shown in Figure 13.3. The SE signal dropped by 37%, which corresponds to an increase in the relaxation rate by 4.8 seconds⁻¹ (TE = 95 milliseconds). If this signal change is analyzed in terms of the three relaxation scales discussed earlier, in an SE experiment, macroscopic effects (from poor shimming, etc.) are fully refocused. The contribution is therefore zero. The maximum possible effect of microscopic relaxation is a complete suppression of the signal of the blood in which the CA is compartmentalized. This follows from the short (molecular) range of interaction of paramagnetic ions with water molecules and from the fast water exchange between plasma and erythrocytes. By assuming an almost homogeneous proton density throughout the brain, it can be concluded that the microscopic relaxation effect of the CA results in a relative signal change of only a few percentages, as blood occupies only a few percentages of a given voxel encompassing brain tissue.

FIGURE 13.3. Drop in the averaged signal in the thalamus of a human following bolus contrast agent injection (double dose) during gradient-echo (GE) and spin-echo (SE) acquisitions with echo times of 23 ms and 95 ms, respectively. (Data from ref. 7.)

The remaining signal change of more than 30% is owing to the mesoscopic effect of CA that spreads outside the blood compartment via magnetic field gradients that are induced by the presence of CA. Thus, the mesoscopic contribution to the total signal change is responsible for most of the signal variations in DSC MRI. The origin of the mesoscopic relaxation rate suggests that it is sensitive to the geometry of the susceptibility-induced magnetic field, which in turn is defined by the geometry of the vascular compartment or the erythrocytes in bulk blood. This argument is supported by both experiments³^,⁴ and theory.⁵^,⁶

Evaluation of the Vessel Caliber

The complexity of the mesoscopic relaxation may appear discouraging, but it offers some benefits. Given a reliable theory, the mesoscopic relaxation promises to provide an interpretation of experimental data (such as in Fig. 13.3) in terms of microvascular geometry, allowing in vivo measurements of the mean caliber of the microvessels.⁷^,⁸^,⁹^,¹⁰ This measurement exploits the difference in the vessel size dependence of the mesoscopic relaxation rate between GE and SE signals. Figure 13.1 shows this dependence for simulated vessels with a fixed volume fraction of 2% as a function of their radii. Theoretical derivations² demonstrate excellent agreement with Monte Carlo simulations.¹

Forward Model of Relaxation

This section discusses the basic mechanisms behind the plots shown in Figure 13.1. Vessels containing paramagnetic CA induce a magnetic field around them. The magnitude of this field on the surface of these vessels is independent of the vessel size, and it attenuates with increasing distance from the vessels. The field perturbations caused by small vessels (left side in Fig. 13.1) vary rapidly in space, thus diffusing water molecules experience a rapidly changing magnetic field with a correlation time that is much shorter than the echo time (60 ms and 100 milliseconds for GE and SE measurements, respectively). This results in effective averaging of the variable magnetic field (small relaxation rate) and explains the similarities between GE and SE relaxation for small vessels. This limiting case is called diffusion narrowing regime (DNR) or motion narrowing regime (see Chapter 11 for additional details).

The GE signal is constant for large vessels, because the spatial pattern of the susceptibility-induced Larmor frequency shifts can be rescaled in proportion to the vessel size. There is an area around each vessel in which the signal is effectively dephased. The size of this area increases with increasing vessel caliber, but the number of vessels decreases to keep the total volume fraction constant. Note that water diffusion does not contribute to a considerable extent to the GE dephasing in this regime because it is effective for large vessels that induce magnetic fields, which varies slowly over the spin’s diffusion length.

In contrast, diffusion is crucial for SE attenuation, because the Larmor frequency offsets can be fully rephased for steady molecules; there would be no SE attenuation if water diffusion were absent. The relaxation rate is determined by the gradients of the vessel-induced magnetic fields across the diffusion lengths of water molecules. These gradients are smaller for larger vessels, which explains the vanishing relaxation for large vessel radii. In terms of sequence timing, TE is much shorter than the correlation time of magnetic field variations experienced by the water molecules in the vicinity of large vessels. For example, the correlation time is about 10 seconds for vessels with 100 μm radii. This limiting case is called static dephasing regime (SDR).

For further analysis, a theoretical model is needed for the GE and SE relaxation rates: R_2,GE and R_2,SE, respectively. A simple model of the microvasculature within brain tissue is the representation of blood vessels as straight, infinitely long cylinders with random positions and orientations.¹¹ The simulated microvasculature is considered monosized with a vessel radius ρ and a volume fraction ζ. VSI is a way to express the relationship between GE and SE relaxation rates in terms of a single parameter, the mean vessel caliber, using models such as the one described in Figure 13.1. Note that the model of straight, infinitely long cylinders is rather simple, but it works well for relaxation theory,¹² but principal limitations apply for diffusion-weighted MRI.¹³

Another relevant parameter is the strength of the magnetic field perturbation caused by paramagnetic vessels, described by δΩ = 2πχγB₀. Quantitatively, δΩ is the maximal Larmor frequency offset at the surface of a cylindrical vessel oriented orthogonally to the main magnetic field. The product γB₀ is the Larmor frequency of water, and χ is the magnetic susceptibility difference between the vessels containing CA and the surrounding tissue. A representative value of magnetic susceptibility is χ = 0.26 ppm for a gadolinium concentration within blood of 10 mmol/L.¹⁴ This results in a frequency offset δΩ/(2π) of 197 Hz. Note that the magnetic susceptibility is given in centimeter-gram-second units. Using SI units, the factor 4π is absorbed in χ in all expressions.

Water diffusion in the extravascular space is assumed to follow a Gaussian distribution for the spin displacement, which is characterized by a diffusion coefficient D. Its typical value in gray matter is D = 0.8·μm²/ms. To the best of our knowledge, anisotropic diffusion in white matter has not been taken into account in theoretical DSC MRI models. The diffusion coefficient, together with the vessel size, results in an estimate of the correlation time of magnetic field fluctuations, τ_D = ρ²/D, as experienced by diffusing water molecules.

In the following equations, only the mesoscopic part of the changes in the transverse relaxation rate caused by the presence of CA in the blood pool is considered. This contribution is measured experimentally by normalizing the signal, S, by its baseline value prior to contrast administration, S₀. Here, the signal attenuation during the bolus passage takes the form

where ΔR₂ stands for either changes in the GE relaxation rate (ΔR_2,GE) or the SE relaxation rate (ΔR_2,SE). The focus here is on the SDR, which is more relevant for practical applications. Then, the attenuation exponents take the following approximate forms¹¹^,¹⁵:

for δΩT_E >> 1, and

for (δΩτ_D)^2/3 T_E/τ_D >> 1.

Signal dephasing falls into the SDR if molecules that are diffusing in close vicinity to a vessel acquire a large phase. This is expressed by the condition δΩτ_D>> 1, because the typical time during which water molecules are close to a vessel is τ_D.

Note that the direct proportionality of the left side of Eqs. 2 and 3 to the blood volume fraction, ζ, is the result of keeping only the first-order term of the Taylor expansion of log(S) with respect to ζ, which is a reasonable
approximation given the small size of this parameter. The factors beyond ζ in Eqs. 2 and 3 depend on two parameter combinations only, δΩτ_D and T_E/τ_D, while δΩT_E is their product. This is a manifestation of a scaling present in the system.²^,¹⁶^,¹⁷

FIGURE 13.4. Simultaneous variation of ΔR_2,GE and ΔR_2,SE^3/2 in Eq. 4 during bolus passage (circles). The origin corresponds to the baseline, while the maximal distance from it corresponds to the peak of the bolus. The static dephasing regime approximation, given by Eqs. 2 and 3, predicts a direct proportionality between these quantities (straight line). In reality, there is a deviation from a linear relationship for small contrast agent concentrations.

Calculation of Vessel Caliber

Eqs. 2 and 3 contain four unknown tissue parameters: vessel radius (ρ), blood volume fraction (ζ), Larmor frequency offset (δΩ), and diffusion coefficient (D). Given the two measured relaxation rates on the left side of Eqs. 2 and 3, two unknowns can be determined, while the remaining two unknowns have to be specified. Specifying ζ and D as known parameters results in an expression for δΩ (not shown) and the following expression for the vessel size:

Choosing δΩ and D as known parameters yields

and another expression for ζ (not shown).

Eqs. 4 and 5 imply two different experimental methods for VSI, called dynamic VSI⁷ and steady state VSI,⁸^,¹⁰ respectively, which are discussed later in the chapter. The evaluated vessel diameter is often referred to as the vessel size index.

The focus of this chapter is on dynamic VSI (see Eq. 4), which is applicable to measurements in human subjects. In principle, Eq. 4 refers to a single, double-contrast measurement. But, given experimental noise, a more robust estimate of the vessel size index is obtained by fitting a proportionality line to the dependence of ΔR_2,GE and ΔR_2,SE^3/2 during the course of the bolus passage (Fig. 13.4). The slope of this line is interpreted as the fraction shown on the right side of Eq. 4. This procedure can be applied to each eligible voxel within the brain. It is worth preceding these calculations with the selection of a subset of voxels in which both GE and SE signals show statistically significant decreases during bolus passage. In this context, the reduced sensitivity of the SE signal to the CA passage is the major limiting factor.

Only gold members can continue reading. Log In or Register to continue