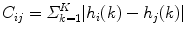Fig. 1
The mouse skeleton as included in the atlas (top) and after segmentation of single bones and adding joints (bottom)(adapted from [2], ©2007 IEEE)
Three types of joints have to be modeled: ball joints, hinge joints and the shoulder complex (both shoulders combined). Table 1 shows the DoFs for the ball and hinge joints. In addition to these anatomically relevant DoFs, three translations for both joint types and two rotations for the hinge joints are allowed to a small extent, to be able to compensate for potential errors that have been made during previous registration of another bone that is rigidly connected. Due to the large number of DoFs in the shoulder, an additional motion constraint has to be introduced for the shoulder by allowing only a coupled, symmetric displacement of both front upper limbs, with a varying distance between the shoulders and a rotation towards and away from each other. Subsequently, the left and the right front upper limb can be decoupled.
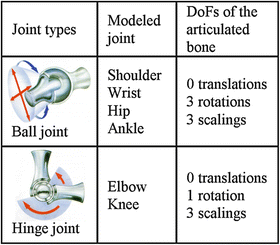
Table 1
Joint types of the atlas skeleton and the DoFs for the registration of the distal articulated bone (Pictograms from [7])
3.2 Hierarchical anatomical model of the skeleton
The hierarchical anatomical tree used for this work is shown in Fig. 2. The strategy to incorporate the entire bone structure is to first align the atlas and the subject skeleton coarsely and then to apply an articulated registration scheme traversing the hierarchical tree. In this way, lower tree levels are initialized and constrained by higher level transformations. The highest hierarchical level is the entire mouse skeleton itself (L0). The skull is placed on the next lower level (L1), because its registration result initializes the matching of all other parts. The rest of the skeleton is divided into three subparts, consisting either of single bones or bone compounds (L2 − L6).
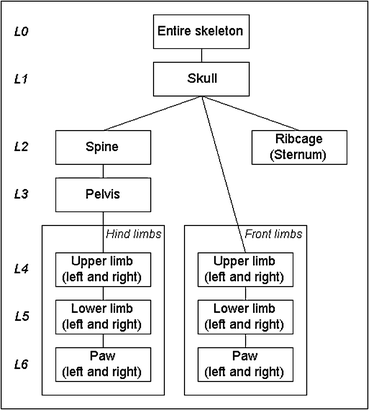
Fig. 2
Hierarchical anatomical tree for the skeleton. The connections depict relations between single bones or bone compounds such that a part on a lower level is initialized by the registration result on a high level (figure adapted from [2], ©2007 IEEE)
These are the rear part consisting of spine, pelvis, upper and lower hind limbs and the paws, the front part consisting of upper and lower front limbs and the paws and the ribcage, represented by the sternum. The relations between all elements in the three subparts are fully determined by rigid connections (joints). Including the shoulder blade into the tree or making further distinctions such as refining the paws is not relevant for the goal of capturing the animal posture and therefore can be omitted. Assuming that the spine and the sternum sufficiently constrain the shape of the ribcage, the ribs can be left out as well.
3.3 Resolving global degrees of freedom
For initialization of the articulated registration, the mouse atlas needs to be coarsely aligned to the skeleton segmented from CT i.e. global DoFs have to be removed. Taking the nodes of a skeleton surface representation as a 3D point set enables to resolve several global DoFs by aligning the principal axes. Subsequent extraction and analysis of a 3D curve that represents the skeleton allows to resolve all other possible global DoFs (refer to Baiker et al. [2] for details).
3.4 3D point matching algorithm for bones and the lung
Two problems arise in matching two point sets: correspondence and transformation. A method that solves for both simultaneously is the Iterative Closest Point (ICP) algorithm (Besl et al. [4]). While originally been developed for incorporating rigid transformations only, pilot experiments have shown that non-isotropic scaling can be integrated too as long as it is moderate. In this way, it is possible to account for inter-subject variability. The articulated registration of the skeleton is performed by stepwise traversing the hierarchical anatomical tree (Fig. 2) in a top-down manner. If the correspondence, i.e. the Euclidean distance between the point sets representing the atlas bone and the target bone surfaces respectively does not improve any more within an iteration step, the final transformation function is used to initialize the registration of a bone at a lower hierarchical level. Depending on the joint type, the DoFs for this node level are kinematically constrained. Traversing the tree, the overall correspondence improves gradually. The lung is registered in the same way as the bones including non-isotropic scaling, to account for shape variations due to breathing.
There is one exception to the registration scheme. Due to its high flexibility, the spine is not determined by registration but by binning the bone point set along its longitudinal axis and applying three dimensional region growing using the head-spine connection as seed point after the head is registered. The number of bone voxels per bin enables to determine the spine-pelvis connection and therefore to initialize the pelvis registration.
3.5 Determination of corresponding landmarks on the skin
Establishing correspondence between two point sets representing skin surfaces in the most general case is very difficult. This is because depending on how the animal is placed during acquisition, the shape can be almost rotation-symmetric to the longitudinal axis of the body, symmetric to the sagittal plane or even almost symmetric to the transverse plane. Furthermore, the shape of an animal can differ significantly e.g. if two mice are positioned in prone and supine position respectively.
The first issue can be resolved directly, if a registered skeleton is at hand. Then it is possible to determine a sparse set of corresponding landmarks on the surface of the animal skin by calculating the nodes with the smallest Euclidean distance from a set of bone landmarks. Having defined a sparse landmark set allows removing ambiguity during matching. The second issue can be resolved by taking surface information into account and relying on a local shape context to identify corresponding nodes. The idea of matching shapes based on global shape contexts has been introduced by Belongie et al. [3]. However to be able to take local shape deformation into account, the representation has to be bending invariant. Using geodesic instead of Euclidean distances in a local context allows rendering the representation rotation, translation and bending invariant. Scaling invariance can be achieved as well, by normalization of the geodesic distances.
Let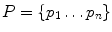 
and 
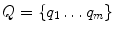be the nodes of two surfaces to be matched and h i and h j be the histograms of geodesic distances from nodes p i ∈ P and q j ∈ Q to other nodes of the surface. The method to find dense correspondence on the skin is as follows:
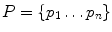and 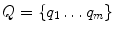be the nodes of two surfaces to be matched and h i and h j be the histograms of geodesic distances from nodes p i ∈ P and q j ∈ Q to other nodes of the surface. The method to find dense correspondence on the skin is as follows:1.
Initialize a list with corresponding skin nodes that are known (landmarks derived from skeleton registration)
Repeat steps 2-7 for all elements in the correspondence list:
2.
Select all nodes on P and Q in the vicinity (i.e. between a maximum and minimum geodesic distance and with a minimum distance to already known correspondences of the next element on the list
3.
Calculate a local shape context based on geodesic distances towards K known corresponding nodes for the selected nodes in P and Q
Repeat steps 4-7 until no selected nodes are left:
4.
Get Clinical Tree app for offline access
Calculate the cost for matching two nodes p i and q j by calculating the distance of their histograms:
