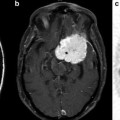
Fig. 11.1
Three modes of water diffusion within brain tissue are shown. The isotropic and single fiber anisotropic patterns are relatively simple and can be accurately characterized with diffusion tensor imaging and advanced diffusion MR. Complex white matter with two or more crossing fiber populations requires an advanced diffusion MR approach to discriminate the orientation and properties of each fiber population. It is important to note that advanced diffusion MR can also be used to depict the isotropic and single fiber anisotropic architectures

Fig. 11.2
A section of the frontal lobe at the intersection of the corpus callosum with other deep white matter tracts. DTI (left) and q-ball HARDI (right) reconstructions of the same data are shown. Within the corpus callosum (bottom right of each panel) both DTI and HARDI accurately identify the single fiber population. However, in the center of each panel, the callosal fibers intersect, cross, or interdigitate with other white matter tracts. The DTI model fails to accurately portray the complex architecture. The q-ball reconstructions indicate the presence of multiple crossing fibers with different orientations and patterns of connectivity. Each peak of the q-ball HARDI glyph represents an axonal bundle
All major commissural and projection brain tracts have architectures which vary from simple to complex along their length. DTI can successful depict white matter architecture where there exists a single or dominant fiber population. Advanced diffusion MR technique development has been a priority for many research groups because it is one of the only noninvasive methods of studying white matter architecture and connectivity through all regions of the brain. The improvements gained with advanced diffusion MR strongly motivate rapid translation of clinical applications.
Part 2: Overview of Advanced Diffusion MR Techniques
This section provides an overview of the different advanced diffusion methods capable of detecting multiple crossing fiber populations. All diffusion MR experiments have both a data MR acquisition component and a software post-processing component. Diffusion MR can characterize tissue microstructure at a level of detail ultimately dictated by the quality and length of the data acquisition. The type of data acquired during a diffusion MR scan determines which post-processing fiber crossing techniques can be chosen.
The diffusion-weighted images acquired for DTI and advanced diffusion MR methods are very similar. Multiple diffusion-weighted volumes are acquired which have image intensity sensitive to the Brownian motion in a particular direction. The two parameters of diffusion-weighted imaging that dictate which post-processing methods can be used are the number of diffusion gradient directions and the level of diffusion sensitivity. DTI only requires a minimum of six directions of diffusion weighting for its single fiber model [6]. Advanced diffusion methods require dozens or hundreds of gradient directions to provide angular resolution between multiple fibers. The level of diffusion sensitivity, termed the b-value, can be increased to improve angular resolution between fibers. DTI typically uses a b-value of 1,000 s/mm2 while advanced diffusion MR may use much higher b-values.
For simplicity, post-processing techniques can be categorized into diffusion spectrum imaging (DSI) and HARDI methods. Unlike DTI, the software for DSI and HARDI post-processing cannot typically be found on commercial MR or surgical navigation systems. The following sections outline the fundamental concepts of how advanced diffusion MR infers tissue structure.
Diffusion Spectrum Imaging
DSI does not rely on any predefined models of water diffusion and does not assume a Gaussian pattern of diffusion. DSI attempts to measure the entire 3D probability density function (PDF) of water diffusion [7]. The PDF describes how likely it is for a water molecule to move a particular distance and orientation from its starting point during a diffusion experiment. This level of detailed information on tissue microstructure requires long imaging times. The acquisition includes hundreds of diffusion-weighted images that probe diffusion in hundreds of different directions and at many levels of diffusion sensitivity (b-values).
The fundamental relationship between the PDF(r) and the diffusion-weighted data S(q) from a single voxel is
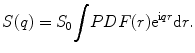
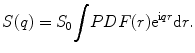
S 0 is the signal intensity without diffusion weighting, r is a position vector, and q is the diffusion gradient vector. PDF(r) can be solved for by performing a 3D Fourier transform on S(q).
Validation studies for DSI have been performed in manganese-enhanced rat optic tracts [8]. Kuo et al. determined which DSI parameters optimize the accuracy and precision of measured fiber orientation on a 3T clinical scanner [9]. The study found that a maximum b-value of 6,500 s/mm2 was optimal for DSI with 515 sampling points and a maximum b-values of 4,000 s/mm2 was optimal for DSI with 203 sampling points. It was also determined that DSI with 203 sampling points could be acquired in about 30 min and produce results with a similar accuracy to DSI with 515 sampling points. Further studies have used a simultaneous image refocusing echo planar pulse sequence to significantly decrease the imaging time by acquiring two adjacent slices during each readout [10]. Decreased MR acquisition times may improve the feasibility of including DSI in a surgical planning protocol.
HARDI
For applications such as fiber tractography, it is not necessary to measure all of q-space and calculate a detailed PDF. Only the orientation of the axonal bundles is necessary to conduct fiber tractography. The 3D PDF can be mathematically collapsed into a 2D orientation distribution function, ODF (u). The ODF describes the probability of water molecules diffusing in a direction described by unit vector u. HARDI methods estimate the ODF or fiber orientations without the time intensive acquisition of DSI.
As with DSI, HARDI probes diffusion in many more directions than DTI. Unlike DSI, HARDI only requires diffusion-weighted images at a single b-value. Thus, HARDI scan times are much more feasible for research or clinical use. Figure 11.3 compares the acquisition requirements of a typical HARDI experiment to that of DTI. There are a number of post-processing algorithms described in the literature which can take raw HARDI data and calculate the orientation of multiple fiber populations. All are based upon the underlying principal that diffusion along axonal bundles is less restricted than diffusion transverse to diffusion bundles.
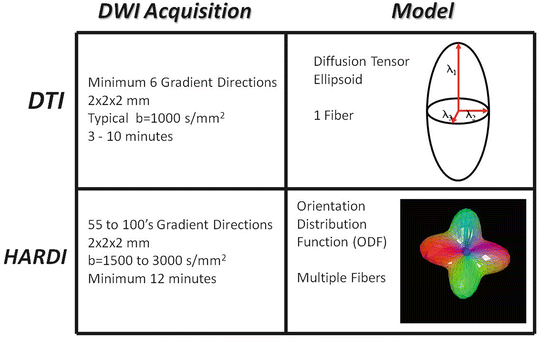

Fig. 11.3
Comparison of DTI and HARDI acquisitions and the models which are produced. The parameters of the diffusion-weighted acquisitions are typical of sequences used in diagnostic MR exams or clinical research
The q-ball reconstruction of HARDI data is a model-free method of estimating the ODF [11–13]. The ODF can be directly estimated from a single spherical shell in q-space with the Funk-Radon transform as follows:
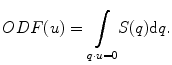
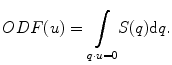
To evaluate the ODF in direction u, the diffusion-weighted signals S(q) are integrated along an equator perpendicular to u. The Funk-Radon transform can be challenging to directly implement, because S(q) is limited to the finite number of diffusion-weighted images acquired. Spherical harmonics can be used to model S(q) and analytically compute the Funk-Radon transform without additional interpolation to estimate the ODF [14].
The spherical deconvolution technique generates a fiber orientation distribution from HARDI data [15]. This technique is model-based as it assumes a particular response function for each component fiber population. The diffusion-weighted signal from a voxel with multiple fiber bundles is modeled as a linear combination of multiple response functions. This combined signal can be deconvolved to determine the number and orientation of the fiber populations. Spherical deconvolution can be combined with linear regularization to remove spurious peaks on the fiber orientation distribution [16]. Spherical convolution achieves high angular resolution; however the method is susceptible to errors in regions of the brain where neuronal tissue does not conform to the assumed response function.
Numerous other methods have been proposed to analyze complex diffusion patterns with HARDI. The apparent diffusion coefficient profile can also be represented with spherical harmonic basic functions to detect multiple fiber populations [4]. Diffusion can be modeled with multiple tensors [17] or as multiple axially symmetric tensors [18]. The diffusion orientation transform is a method of estimating the displacement probability function directly from the HARDI data [19].
Hybrid diffusion imaging (HYDI) is an acquisition strategy that allows DTI, DSI, and q-ball post-processing techniques to be performed on the same limited data set [20]. Multiple concentric q-space shells are acquired with approximately 100 points spanning b-values from about 375 to 9,500 s/mm2. The diffusion tensor can be calculated from the data with diffusion weighting of under 2,000 s/mm2. The q-ball ODF is constructed with data from a single shell with high diffusion weighting. DSI can be performed with all the acquired q-space data.
Part 3: Clinical Translation of HARDI
Fiber Tracking with Multiple Fibers
DTI tractography has become a standard of care for the presurgical localization of functionally important white matter tracts [21–26]. However, the limitations of the diffusion tensor model translate into the inability of DTI fiber tracking to robustly traverse regions of complex white matter [3]. Many tractography algorithms have been proposed to take advantage of multiple propagators provided by advanced diffusion MR [3, 27–33]. Much like DTI tractography, these new algorithms can be deterministic or probabilistic. Deterministic algorithms typically propagate fiber trajectories along the best estimate of axonal orientation. Probabilistic algorithms propagate trajectories in multiple alternative directions by incorporating an estimate of fiber orientation uncertainty. All tractography algorithms are ultimately based upon the fundamental assumption that water diffusion is correlated with axon orientation.
Figure 11.4 demonstrates the ability of probabilistic q-ball HARDI tractography to delineate a larger portion of the motor tract than DTI tractography. This HARDI algorithm uses the residual bootstrap to estimate uncertainty in the orientation of the q-ball ODFs [28]. Both DTI and HARDI tractography are able to connect the superior-medial section of the motor cortex to the midbrain. However, HARDI tractography improves the ability to identify the portion of the motor system connected to the inferior-lateral portion of the motor cortex. The lateral sections of the motor cortex controls head and face motions. These cortices are functionally important and mouth motor is critical for speaking and language function. The white matter carrying these functions can be visualized with HARDI tractography in relation to the subcortical lesion borders. Figure 11.5 shows another comparison between DTI motor tractography and HARDI tractography. In this case, the HARDI tractography passes through the lesion and delineates connections to the lateral motor cortex. The DTI fiber tractography remains in the core of motor pathway and does not turn off to connect to the lateral motor cortex.
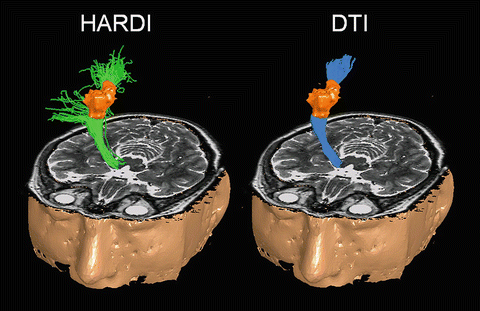
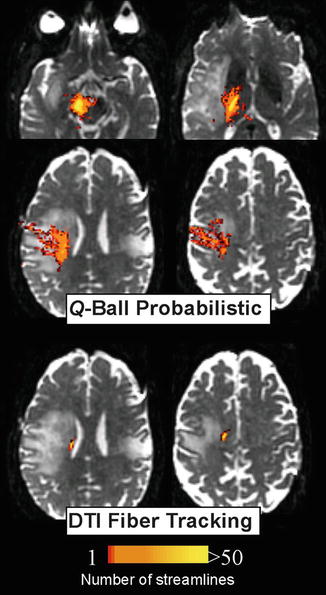

Fig. 11.4
HARDI tracrography of the motor system (green streamlines on left) is compared to DTI tractography (blue streamlines on right). The lesion is in orange. (Figure adapted from Berman 2009 [45])

Fig. 11.5
Comparison between HARDI (q-ball) probabilistic tractography and DTI fiber tracking of the motor pathway in an adult brain tumor patient. HARDI tractography courses laterally through the centrum semiovale through the lesion to the lateral motor cortex
The motor tract, like other major white matter tracts, has heterogeneous microstructure. The main trunk of the motor track, within the cerebral peduncle and internal capsule, is a large bundle of axons with no major crossing fibers. DTI and HARDI tractography can both easily follow the tract through the internal capsule, to the centrum semiovale. The portion of the motor pathway connecting the superior-medial motor cortex to the internal capsule is still a dominant pathway and can be visualized with DTI tractography. However, the centrum semiovale contains multiple crossing white matter tracts including the motor pathway, superior longitudinal fasciculus, and the corpus callosum. DTI cannot consistently traverse the motor pathway laterally within this region of complex architecture. This shortcoming of DTI within the centrum semiovale explains the improvements gained with HARDI motor tractography. Figure 11.6 exhibits in detail the performance of DTI and HARDI at this point along the motor pathway.


Fig. 11.6
Close-up of the centrum semiovale with HARDI (left) and DTI color overlay (right). The DTI image shows only a single dominant fiber pathway per voxel. However, the q-ball HARDI reconstruction shows the intersection of the superior longitudinal fasciculus (SLF, green) and motor tract (red in gyrus, blue in internal capsule)
Combination with Functional Mapping
Diffusion MR tractography is not sensitive to neuronal activation and provides no information on brain function. Tractography is strictly a structural method which cannot inherently distinguish different white matter tracts. Functional information must be added to create a starting region of interest within a specific white matter tract. This functional information can simply come from a textbook or atlas describing the brain’s organization. Alternatively, subject-specific mapping techniques such as fMRI, magnetoencephalography, or electrocorticography can be used to locate specific cortices [34–40




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree