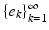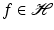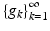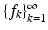. We pay special attention to the case d = 2, which is the most important case for image processing and image analysis applications.
The chapter is organized as follows. Section 2 presents central tools from functional analysis in Hilbert spaces, e.g., the pseudo-inverse of a bounded operator and the central facts from frame theory. In Sect. 3, we introduce several operators that play important roles in Gabor analysis. Gabor frames on 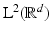 are introduced in Sect. 4, and their discrete counterpart are treated in Sect. 5. Finally, the application of Gabor expansions to image representation is considered in Sect. 6.
are introduced in Sect. 4, and their discrete counterpart are treated in Sect. 5. Finally, the application of Gabor expansions to image representation is considered in Sect. 6.
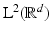 are introduced in Sect. 4, and their discrete counterpart are treated in Sect. 5. Finally, the application of Gabor expansions to image representation is considered in Sect. 6.
are introduced in Sect. 4, and their discrete counterpart are treated in Sect. 5. Finally, the application of Gabor expansions to image representation is considered in Sect. 6.2 Tools from Functional Analysis
In this section, we recall basic facts from functional analysis. Unless another reference is given, a proof can be found in [17]. In the entire section, 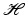 denotes a separable Hilbert space with inner product
denotes a separable Hilbert space with inner product 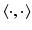 .
.
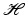 denotes a separable Hilbert space with inner product
denotes a separable Hilbert space with inner product 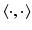 .
.The Pseudo-inverse Operator
It is well known that an arbitrary matrix has a pseudo-inverse, which can be used to find the minimal-norm least squares solution of a linear system. In the case of an operator on infinite-dimensional Hilbert spaces, one has to restrict the attention to linear operators with closed range in order to obtain a pseudo-inverse. Observe that a bounded operator (We will always assume linearity!) U on a Hilbert space 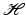 is invertible if and only if it is injective and surjective, while injectivity combined with a dense range is not sufficient in the infinite-dimensional case. However, if the range of U is closed, there exists a “right-inverse operator” U † in the following sense:
is invertible if and only if it is injective and surjective, while injectivity combined with a dense range is not sufficient in the infinite-dimensional case. However, if the range of U is closed, there exists a “right-inverse operator” U † in the following sense:
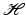 is invertible if and only if it is injective and surjective, while injectivity combined with a dense range is not sufficient in the infinite-dimensional case. However, if the range of U is closed, there exists a “right-inverse operator” U † in the following sense:
is invertible if and only if it is injective and surjective, while injectivity combined with a dense range is not sufficient in the infinite-dimensional case. However, if the range of U is closed, there exists a “right-inverse operator” U † in the following sense: Lemma 1.
Let 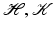 be Hilbert spaces, and suppose that
be Hilbert spaces, and suppose that 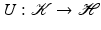 is a bounded operator with closed range
is a bounded operator with closed range 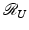 . Then there exists a bounded operator
. Then there exists a bounded operator 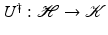 for which
for which
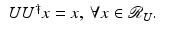
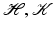 be Hilbert spaces, and suppose that
be Hilbert spaces, and suppose that 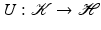 is a bounded operator with closed range
is a bounded operator with closed range 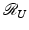 . Then there exists a bounded operator
. Then there exists a bounded operator 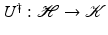 for which
for which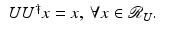
(1)
Proof.
Consider the operator obtained by taking the restriction of U to the orthogonal complement of the kernel of U, i.e., let
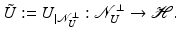 Obviously,
Obviously, 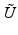 is linear and bounded.
is linear and bounded. 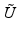 is also injective: if
is also injective: if 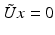 , it follows that
, it follows that 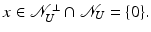 We prove next that the range of
We prove next that the range of 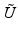 equals the range of U. Given
equals the range of U. Given 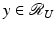 , there exists
, there exists 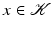 such that Ux = y. By writing x = x 1 + x 2, where
such that Ux = y. By writing x = x 1 + x 2, where 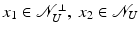 , we obtain that
, we obtain that
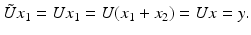 It follows from Banach’s theorem that
It follows from Banach’s theorem that 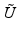 has a bounded inverse
has a bounded inverse
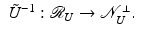 Extending
Extending 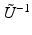 by zero on the orthogonal complement of
by zero on the orthogonal complement of 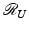 , we obtain a bounded operator
, we obtain a bounded operator 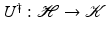 for which UU † x = x for all
for which UU † x = x for all 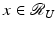 . ■
. ■
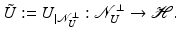
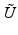 is linear and bounded.
is linear and bounded. 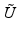 is also injective: if
is also injective: if 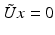 , it follows that
, it follows that 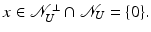 We prove next that the range of
We prove next that the range of 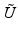 equals the range of U. Given
equals the range of U. Given 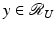 , there exists
, there exists 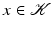 such that Ux = y. By writing x = x 1 + x 2, where
such that Ux = y. By writing x = x 1 + x 2, where 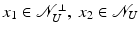 , we obtain that
, we obtain that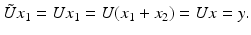
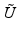 has a bounded inverse
has a bounded inverse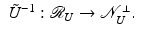
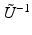 by zero on the orthogonal complement of
by zero on the orthogonal complement of 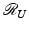 , we obtain a bounded operator
, we obtain a bounded operator 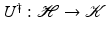 for which UU † x = x for all
for which UU † x = x for all 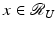 . ■
. ■ The operator U † constructed in the proof of Lemma 1 is called the pseudo-inverse of U. In the literature, one will often see the pseudo-inverse of an operator U defined as the unique operator U † satisfying that
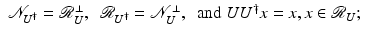
this definition is equivalent to the above construction. We collect some properties of U † and its relationship to U.
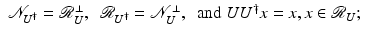
(2)
Lemma 2.
Let 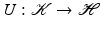 be a bounded operator with closed range. Then the following holds:
be a bounded operator with closed range. Then the following holds:
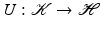 be a bounded operator with closed range. Then the following holds:
be a bounded operator with closed range. Then the following holds:(i)
The orthogonal projection of 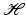 onto
onto 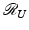 is given by UU †.
is given by UU †.
 onto
onto 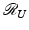 is given by UU †.
is given by UU †.(ii)
The orthogonal projection of  onto
onto 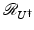 is given by U † U.
is given by U † U.
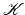 onto
onto 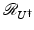 is given by U † U.
is given by U † U. (iii)
U ∗ has closed range, and (U ∗ ) † = (U † ) ∗.
(iv)
On 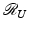 , the operator U † is given explicitly by
, the operator U † is given explicitly by
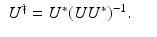
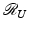 , the operator U † is given explicitly by
, the operator U † is given explicitly by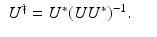
(3)
Bessel Sequences in Hilbert Spaces
When we deal with infinite-dimensional vector spaces, we need to consider expansions in terms of infinite series. The purpose of this section is to introduce a condition that ensures that the relevant infinite series actually converge. When speaking about a sequence 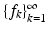 in
in  , we mean an ordered set, i.e.,
, we mean an ordered set, i.e., 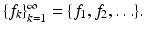 That we have chosen to index the sequence by the natural numbers is just for convenience.
That we have chosen to index the sequence by the natural numbers is just for convenience.
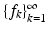 in
in  , we mean an ordered set, i.e.,
, we mean an ordered set, i.e., 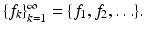 That we have chosen to index the sequence by the natural numbers is just for convenience.
That we have chosen to index the sequence by the natural numbers is just for convenience.Definition 1.
A sequence 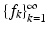 in
in 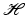 is called a Bessel sequence if there exists a constant B > 0 such that
is called a Bessel sequence if there exists a constant B > 0 such that
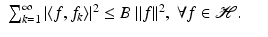
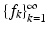 in
in 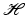 is called a Bessel sequence if there exists a constant B > 0 such that
is called a Bessel sequence if there exists a constant B > 0 such that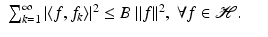
(4)
Any number B satisfying (4) is called a Bessel bound for 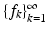 . The optimal bound for a given Bessel sequence
. The optimal bound for a given Bessel sequence 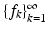 is the smallest possible value of B > 0 satisfying (4). Except for the case
is the smallest possible value of B > 0 satisfying (4). Except for the case 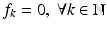 , the optimal bound always exists.
, the optimal bound always exists.
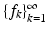 . The optimal bound for a given Bessel sequence
. The optimal bound for a given Bessel sequence 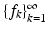 is the smallest possible value of B > 0 satisfying (4). Except for the case
is the smallest possible value of B > 0 satisfying (4). Except for the case 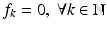 , the optimal bound always exists.
, the optimal bound always exists.Theorem 1.
Let 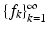 be a sequence in
be a sequence in 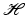 and B > 0 be given. Then
and B > 0 be given. Then 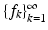 is a Bessel sequence with Bessel bound B if and only if
is a Bessel sequence with Bessel bound B if and only if
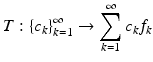 defines a bounded operator from
defines a bounded operator from 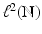 into
into 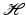 and
and 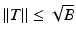 .
.
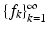 be a sequence in
be a sequence in 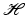 and B > 0 be given. Then
and B > 0 be given. Then 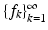 is a Bessel sequence with Bessel bound B if and only if
is a Bessel sequence with Bessel bound B if and only if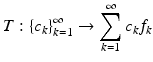
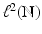 into
into 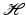 and
and 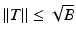 .
.The operator T is called the synthesis operator. The adjoint T ∗ is called the analysis operator and is given by
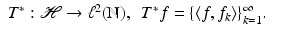 These operators play key roles in the theory of frames, to be considered in section “Frames and Their Properties.”
These operators play key roles in the theory of frames, to be considered in section “Frames and Their Properties.”
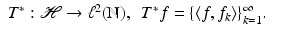
The Bessel condition (4) remains the same, regardless of how the elements 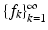 are numbered. This leads to a very important consequence of Theorem 1:
are numbered. This leads to a very important consequence of Theorem 1:
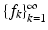 are numbered. This leads to a very important consequence of Theorem 1:
are numbered. This leads to a very important consequence of Theorem 1:Corollary 1.
If 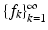 is a Bessel sequence in
is a Bessel sequence in  , then
, then 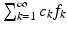 converges unconditionally for all
converges unconditionally for all 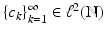 , i.e., the series is convergent, irrespective of how and in which order the summation is realized.
, i.e., the series is convergent, irrespective of how and in which order the summation is realized.
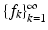 is a Bessel sequence in
is a Bessel sequence in 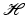 , then
, then 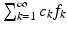 converges unconditionally for all
converges unconditionally for all 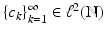 , i.e., the series is convergent, irrespective of how and in which order the summation is realized.
, i.e., the series is convergent, irrespective of how and in which order the summation is realized. Thus, a reordering of the elements in 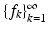 will not affect the series
will not affect the series 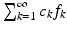 when
when 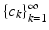 is reordered the same way: the series will converge toward the same element as before. For this reason, we can choose an arbitrary indexing of the elements in the Bessel sequence; in particular, it is not a restriction that we present all results with the natural numbers as index set. As we will see in the sequel, all orthonormal bases and frames are Bessel sequences.
is reordered the same way: the series will converge toward the same element as before. For this reason, we can choose an arbitrary indexing of the elements in the Bessel sequence; in particular, it is not a restriction that we present all results with the natural numbers as index set. As we will see in the sequel, all orthonormal bases and frames are Bessel sequences.
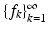 will not affect the series
will not affect the series 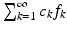 when
when 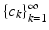 is reordered the same way: the series will converge toward the same element as before. For this reason, we can choose an arbitrary indexing of the elements in the Bessel sequence; in particular, it is not a restriction that we present all results with the natural numbers as index set. As we will see in the sequel, all orthonormal bases and frames are Bessel sequences.
is reordered the same way: the series will converge toward the same element as before. For this reason, we can choose an arbitrary indexing of the elements in the Bessel sequence; in particular, it is not a restriction that we present all results with the natural numbers as index set. As we will see in the sequel, all orthonormal bases and frames are Bessel sequences. General Bases and Orthonormal Bases
We will now briefly consider bases in Hilbert spaces. In particular, we will discuss orthonormal bases, which are the infinite-dimensional counterparts of the canonical bases in 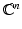 . Orthonormal bases are widely used in mathematics as well as physics, signal processing, and many other areas where one needs to represent functions in terms of “elementary building blocks.”
. Orthonormal bases are widely used in mathematics as well as physics, signal processing, and many other areas where one needs to represent functions in terms of “elementary building blocks.”
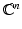 . Orthonormal bases are widely used in mathematics as well as physics, signal processing, and many other areas where one needs to represent functions in terms of “elementary building blocks.”
. Orthonormal bases are widely used in mathematics as well as physics, signal processing, and many other areas where one needs to represent functions in terms of “elementary building blocks.”Definition 2.
Consider a sequence 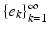 of vectors in
of vectors in 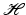 .
.
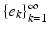 of vectors in
of vectors in 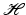 .
.(i)
The sequence 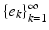 is a (Schauder) basis for
is a (Schauder) basis for 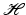 if for each
if for each 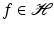 , there exist unique scalar coefficients
, there exist unique scalar coefficients 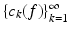 such that
such that
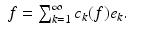
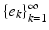 is a (Schauder) basis for
is a (Schauder) basis for 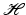 if for each
if for each 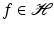 , there exist unique scalar coefficients
, there exist unique scalar coefficients 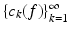 such that
such that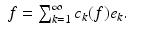
(5)
(iii)
A basis 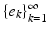 is an orthonormal basis if
is an orthonormal basis if 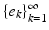 is an orthonormal system, i.e., if
is an orthonormal system, i.e., if
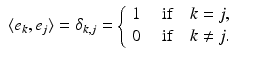
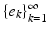 is an orthonormal basis if
is an orthonormal basis if 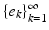 is an orthonormal system, i.e., if
is an orthonormal system, i.e., if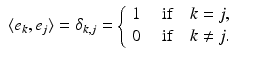
An orthonormal basis leads to an expansion of the type (5) with an explicit expression for the coefficients c k (f):
Theorem 2.
If 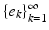 is an orthonormal basis, then each
is an orthonormal basis, then each 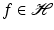 has an unconditionally convergent expansion
has an unconditionally convergent expansion
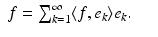
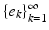 is an orthonormal basis, then each
is an orthonormal basis, then each 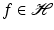 has an unconditionally convergent expansion
has an unconditionally convergent expansion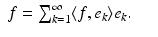
(6)
In practice, orthonormal bases are certainly the most convenient bases to use: for other types of bases, the representation (6) has to be replaced by a more complicated expression. Unfortunately, the conditions for 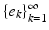 being an orthonormal basis are strong, and often it is impossible to construct orthonormal bases satisfying extra conditions. We discuss this in more detail later. Note also that it is not always a good idea to use the Gram–Schmidt orthonormalization procedure to construct an orthonormal basis from a given basis: it might destroy special properties of the basis at hand. For example, the special structure of a Gabor basis (to be discussed later) will be lost.
being an orthonormal basis are strong, and often it is impossible to construct orthonormal bases satisfying extra conditions. We discuss this in more detail later. Note also that it is not always a good idea to use the Gram–Schmidt orthonormalization procedure to construct an orthonormal basis from a given basis: it might destroy special properties of the basis at hand. For example, the special structure of a Gabor basis (to be discussed later) will be lost.
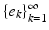 being an orthonormal basis are strong, and often it is impossible to construct orthonormal bases satisfying extra conditions. We discuss this in more detail later. Note also that it is not always a good idea to use the Gram–Schmidt orthonormalization procedure to construct an orthonormal basis from a given basis: it might destroy special properties of the basis at hand. For example, the special structure of a Gabor basis (to be discussed later) will be lost.
being an orthonormal basis are strong, and often it is impossible to construct orthonormal bases satisfying extra conditions. We discuss this in more detail later. Note also that it is not always a good idea to use the Gram–Schmidt orthonormalization procedure to construct an orthonormal basis from a given basis: it might destroy special properties of the basis at hand. For example, the special structure of a Gabor basis (to be discussed later) will be lost. Frames and Their Properties
We are now ready to introduce one of the central subjects:
Definition 3.
A sequence 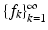 of elements in
of elements in 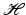 is a frame for
is a frame for 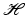 if there exist constants A, B > 0 such that
if there exist constants A, B > 0 such that
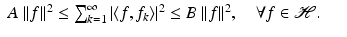
 of elements in
of elements in 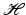 is a frame for
is a frame for 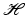 if there exist constants A, B > 0 such that
if there exist constants A, B > 0 such that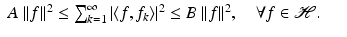
(7)
The numbers A and B are called frame bounds . A special role is played by frames for which the optimal frame bounds coincide:
Definition 4.
A sequence 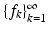 in
in 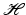 is a tight frame if there exists a number A > 0 such that
is a tight frame if there exists a number A > 0 such that
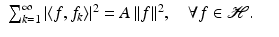 The number A is called the frame bound.
The number A is called the frame bound.
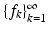 in
in 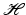 is a tight frame if there exists a number A > 0 such that
is a tight frame if there exists a number A > 0 such that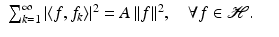
Since a frame 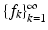 is a Bessel sequence, the operator
is a Bessel sequence, the operator
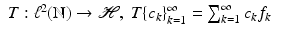
is bounded by Theorem 1. Composing T and T ∗, we obtain the frame operator
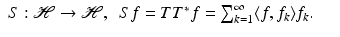
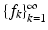 is a Bessel sequence, the operator
is a Bessel sequence, the operator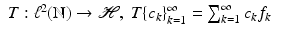
(8)
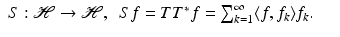
(9)
The frame decomposition, stated in (10) below, is the most important frame result. It shows that if 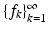 is a frame for
is a frame for 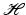 , then every element in
, then every element in 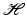 has a representation as an infinite linear combination of the frame elements. Thus, it is natural to view a frame as a “generalized basis.”
has a representation as an infinite linear combination of the frame elements. Thus, it is natural to view a frame as a “generalized basis.”
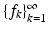 is a frame for
is a frame for 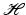 , then every element in
, then every element in 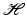 has a representation as an infinite linear combination of the frame elements. Thus, it is natural to view a frame as a “generalized basis.”
has a representation as an infinite linear combination of the frame elements. Thus, it is natural to view a frame as a “generalized basis.”Theorem 3.
Let 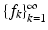 be a frame with frame operator S. Then
be a frame with frame operator S. Then
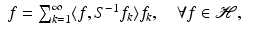
and
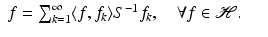
Both series converge unconditionally for all 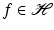 .
.
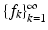 be a frame with frame operator S. Then
be a frame with frame operator S. Then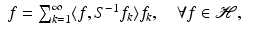
(10)
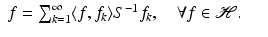
(11)
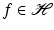 .
.Theorem 3 shows that all information about a given vector 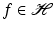 is contained in the sequence
is contained in the sequence 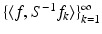 . The numbers
. The numbers 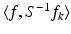 are called frame coefficients. The sequence
are called frame coefficients. The sequence 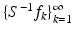 is also a frame; it is called the canonical dual frame of
is also a frame; it is called the canonical dual frame of 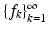 .
.
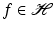 is contained in the sequence
is contained in the sequence 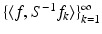 . The numbers
. The numbers 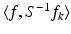 are called frame coefficients. The sequence
are called frame coefficients. The sequence 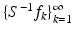 is also a frame; it is called the canonical dual frame of
is also a frame; it is called the canonical dual frame of 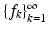 .
.Theorem 3 also immediately reveals one of the main difficulties in frame theory. In fact, in order for the expansions (10) and (11) to be applicable in practice, we need to be able to find the operator S −1 or at least to calculate its action on all 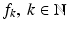 . In general, this is a major problem. One way of circumventing the problem is to consider only tight frames:
. In general, this is a major problem. One way of circumventing the problem is to consider only tight frames:
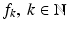 . In general, this is a major problem. One way of circumventing the problem is to consider only tight frames:
. In general, this is a major problem. One way of circumventing the problem is to consider only tight frames:Corollary 2.
If 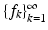 is a tight frame with frame bound A, then the canonical dual frame is
is a tight frame with frame bound A, then the canonical dual frame is 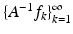 , and
, and
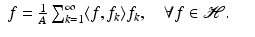
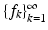 is a tight frame with frame bound A, then the canonical dual frame is
is a tight frame with frame bound A, then the canonical dual frame is 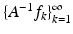 , and
, and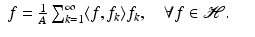
(12)
By a suitable scaling of the vectors 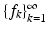 in a tight frame, we can always obtain that A = 1; in that case, (12) has exactly the same form as the representation via an orthonormal basis; see (6). Thus, such frames can be used without any additional computational effort compared with the use of orthonormal bases; however, the family does not have to be linearly independent now.
in a tight frame, we can always obtain that A = 1; in that case, (12) has exactly the same form as the representation via an orthonormal basis; see (6). Thus, such frames can be used without any additional computational effort compared with the use of orthonormal bases; however, the family does not have to be linearly independent now.
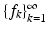 in a tight frame, we can always obtain that A = 1; in that case, (12) has exactly the same form as the representation via an orthonormal basis; see (6). Thus, such frames can be used without any additional computational effort compared with the use of orthonormal bases; however, the family does not have to be linearly independent now.
in a tight frame, we can always obtain that A = 1; in that case, (12) has exactly the same form as the representation via an orthonormal basis; see (6). Thus, such frames can be used without any additional computational effort compared with the use of orthonormal bases; however, the family does not have to be linearly independent now.Tight frames have other advantages. For the design of frames with prescribed properties, it is essential to control the behavior of the canonical dual frame, but the complicated structure of the frame operator and its inverse makes this difficult. If, e.g., we consider a frame 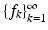 for
for 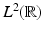 consisting of functions with exponential decay, nothing guarantees that the functions in the canonical dual frame
consisting of functions with exponential decay, nothing guarantees that the functions in the canonical dual frame 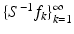 have exponential decay. However, for tight frames, questions of this type trivially have satisfactory answers, because the dual frame equals the original one. Also, for a tight frame, the canonical dual frame automatically has the same structure as the frame itself: if the frame has Gabor structure (to be described in Sect. 4), the same is the case for the canonical dual frame.
have exponential decay. However, for tight frames, questions of this type trivially have satisfactory answers, because the dual frame equals the original one. Also, for a tight frame, the canonical dual frame automatically has the same structure as the frame itself: if the frame has Gabor structure (to be described in Sect. 4), the same is the case for the canonical dual frame.
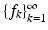 for
for 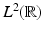 consisting of functions with exponential decay, nothing guarantees that the functions in the canonical dual frame
consisting of functions with exponential decay, nothing guarantees that the functions in the canonical dual frame 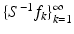 have exponential decay. However, for tight frames, questions of this type trivially have satisfactory answers, because the dual frame equals the original one. Also, for a tight frame, the canonical dual frame automatically has the same structure as the frame itself: if the frame has Gabor structure (to be described in Sect. 4), the same is the case for the canonical dual frame.
have exponential decay. However, for tight frames, questions of this type trivially have satisfactory answers, because the dual frame equals the original one. Also, for a tight frame, the canonical dual frame automatically has the same structure as the frame itself: if the frame has Gabor structure (to be described in Sect. 4), the same is the case for the canonical dual frame.There is another way to avoid the problem of inverting the frame operator S. A frame that is not a basis is said to be overcomplete; in the literature, the term redundant frame is also used. For frames 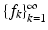 that are not bases, one can replace the canonical dual
that are not bases, one can replace the canonical dual 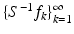 by other frames:
by other frames:
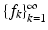 that are not bases, one can replace the canonical dual
that are not bases, one can replace the canonical dual 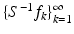 by other frames:
by other frames:Theorem 4.
Assume that 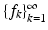 is an overcomplete frame. Then there exist frames
is an overcomplete frame. Then there exist frames 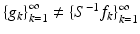 for which
for which
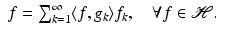
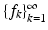 is an overcomplete frame. Then there exist frames
is an overcomplete frame. Then there exist frames 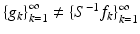 for which
for which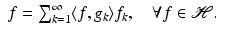
(13)
3 Operators
In this section, we introduce several operators that play key roles in Gabor analysis. In particular, we will need the basic properties of the localized Fourier transform, which is called the STFT (short-time Fourier transform). It is natural for us to start with the Fourier transform, which is defined as an integral transform on the space of all (Lebesgue) integrable functions, denoted by 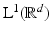 .
.
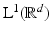 .
.The Fourier Transform
Definition 5.
For 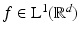 , the Fourier transform is defined as
, the Fourier transform is defined as
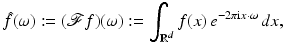
where 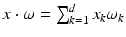 is the usual scalar product of vectors in
is the usual scalar product of vectors in 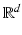 .
.
 , the Fourier transform is defined as
, the Fourier transform is defined as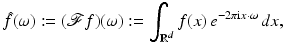
(14)
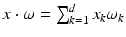 is the usual scalar product of vectors in
is the usual scalar product of vectors in 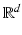 .
.Lemma 3 (Riemann–Lebesgue).
If 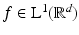 , then
, then 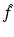 is uniformly continuous and
is uniformly continuous and 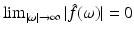 .
.
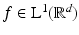 , then
, then 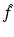 is uniformly continuous and
is uniformly continuous and 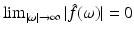 .
.The Fourier transform yields a continuous bijection from the Schwartz space 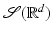 to
to 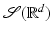 . This follows from the fact that it turns analytic operations (differentiation) into multiplication with polynomials and vice versa:
. This follows from the fact that it turns analytic operations (differentiation) into multiplication with polynomials and vice versa:
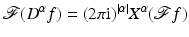
and
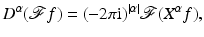
with a multi-index 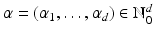 ,
, 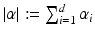 , D α as differential operator
, D α as differential operator
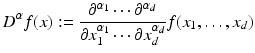 and X α as multiplication operator
and X α as multiplication operator 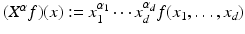 . It follows from the definition that
. It follows from the definition that 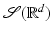 is invariant under these operations, i.e.,
is invariant under these operations, i.e.,
 Using the reflection operator
Using the reflection operator 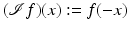 , one can show that
, one can show that 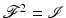 and so
and so 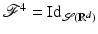 . This yields
. This yields
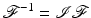
and we can give an inversion formula explicitly:
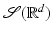 to
to 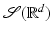 . This follows from the fact that it turns analytic operations (differentiation) into multiplication with polynomials and vice versa:
. This follows from the fact that it turns analytic operations (differentiation) into multiplication with polynomials and vice versa: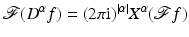
(15)
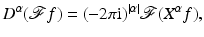
(16)
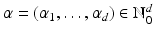 ,
, 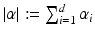 , D α as differential operator
, D α as differential operator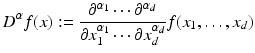
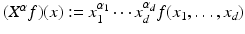 . It follows from the definition that
. It follows from the definition that 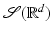 is invariant under these operations, i.e.,
is invariant under these operations, i.e.,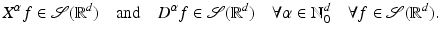
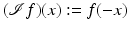 , one can show that
, one can show that 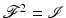 and so
and so 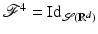 . This yields
. This yields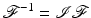
(17)
Theorem 5 (Inversion Formula).
The Fourier transform is a bijection from 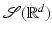 to
to 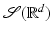 , and the inverse operator is given by
, and the inverse operator is given by
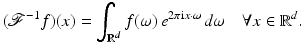
Furthermore,
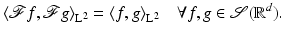
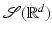 to
to 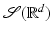 , and the inverse operator is given by
, and the inverse operator is given by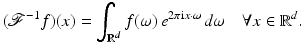
(18)
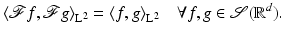
We can extend the Fourier transform to an isometric operator on all of 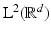 . We will use the same symbol
. We will use the same symbol 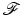 although the Fourier transform on
although the Fourier transform on 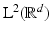 is not defined by a Lebesgue integral (14) anymore if
is not defined by a Lebesgue integral (14) anymore if 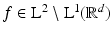 , but rather by means of summability methods. Moreover,
, but rather by means of summability methods. Moreover, 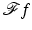 should be viewed as an equivalence class of functions, rather than a pointwise given function.
should be viewed as an equivalence class of functions, rather than a pointwise given function.
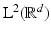 . We will use the same symbol
. We will use the same symbol 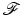 although the Fourier transform on
although the Fourier transform on 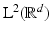 is not defined by a Lebesgue integral (14) anymore if
is not defined by a Lebesgue integral (14) anymore if 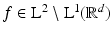 , but rather by means of summability methods. Moreover,
, but rather by means of summability methods. Moreover, 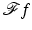 should be viewed as an equivalence class of functions, rather than a pointwise given function.
should be viewed as an equivalence class of functions, rather than a pointwise given function.Theorem 6 (Plancherel).
If 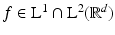 , then
, then
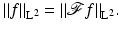
As a consequence, 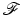 extends in a unique way to a unitary operator on
extends in a unique way to a unitary operator on 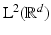 that satisfies Parseval’s formula
that satisfies Parseval’s formula
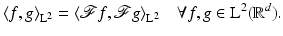
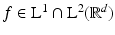 , then
, then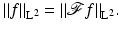
(19)
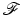 extends in a unique way to a unitary operator on
extends in a unique way to a unitary operator on 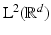 that satisfies Parseval’s formula
that satisfies Parseval’s formula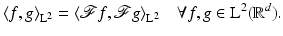
(20)
In signal analysis, the isometry of the Fourier transform has the interpretation that it preserves the energy of a signal. For more details on the role of the Schwartz class for the Fourier transform, see [78, V].
Translation and Modulation
Definition 6.
For 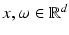 , we define the translation operator T x by
, we define the translation operator T x by
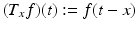
and the modulation operator M ω by
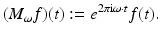
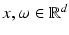 , we define the translation operator T x by
, we define the translation operator T x by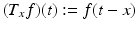
(21)
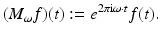
(22)
One has T x −1 = T −x and M ω −1 = M −ω . The operator T x is called a time shift and M ω a frequency shift. Operators of the form T x M ω or M ω T x are called time–frequency shifts (TF-shifts) . They satisfy the commutation relations
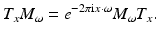
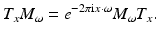
(23)
Time–frequency shifts are isometries on L p for all 1 ≤ p ≤ ∞, i.e.,
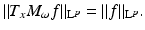 The interplay of TF-shifts with the Fourier transform is as follows:
The interplay of TF-shifts with the Fourier transform is as follows:
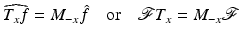
and
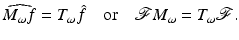
Equation (25) explains why modulations are also called frequency shifts : modulations become translations on the Fourier transform side. Altogether, we have
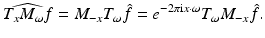
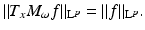
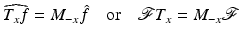
(24)
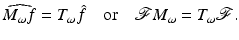
(25)
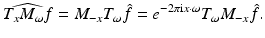
Convolution, Involution, and Reflection
Definition 7.
The convolution of two functions 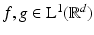 is the function f ∗ g defined by
is the function f ∗ g defined by
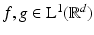 is the function f ∗ g defined by
is the function f ∗ g defined by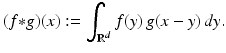
(26)
It satisfies
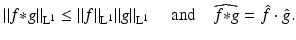 One may view f ∗ g as f being “smeared” by g and vice versa. One can thus smoothen a function by convolving it with a narrow bump function.
One may view f ∗ g as f being “smeared” by g and vice versa. One can thus smoothen a function by convolving it with a narrow bump function.
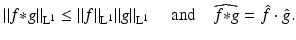
Definition 8.
The involution of a function is defined by
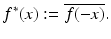
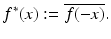
(27)
It follows that
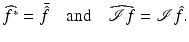 Finally, let us mention that convolution corresponds to pointwise multiplication (and conversely), i.e., the so-called convolution theorem is valid:
Finally, let us mention that convolution corresponds to pointwise multiplication (and conversely), i.e., the so-called convolution theorem is valid:
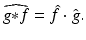
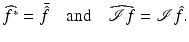
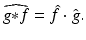
(28)
The Short-Time Fourier Transform
The Fourier transform as described in section “The Fourier Transform” provides only global frequency information of a signal f. This is useful for signals that do not vary during the time, e.g., for analyzing the spectrum of a violin tone. However, dynamic signals such as a melody have to be split into short time intervals over which it can be well approximated by a linear combination of few pure frequencies. Since sharp cutoffs would introduce discontinuities in the localized signal and therefore leaking of the frequency spectrum, a smooth window function g is usually used in the definition of the short-time Fourier transform.
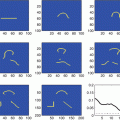
In image processing, one has plane waves instead of pure frequencies; thus, the global Fourier transform is only well suited to stripe-like patterns. Again, a localized version of the Fourier transform allows to determine dominant plane waves locally, and one can reconstruct an image from such a redundant transform. Gabor analysis deals with the question of how one can reconstruct an image from only somewhat overlapping local pieces, which are stored only in the form of a sampled (local) 2D Fourier transform (Fig. 1).
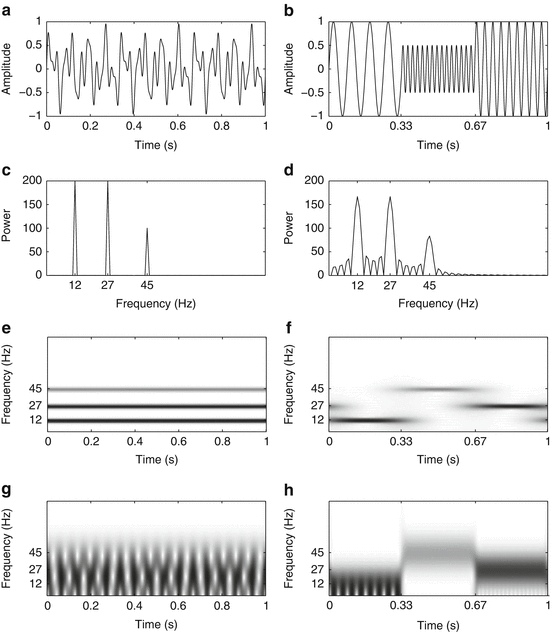

Fig. 1
Two signals and their (short-time) Fourier transforms. (a) Signal 1: Concurrent frequencies. (b) Signal 2: Consecutive frequencies. (c) Fourier power spectrum 1. (d) Fourier power spectrum 2. (e) STFT 1 with wide window. (f) STFT 2 with wide window. (g) STFT 1 with narrow window. (h) STFT 2 with narrow window
Definition 9.
Fix a window function 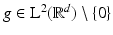 . The short-time Fourier transform (STFT), also called ( continuous ) Gabor transform of a function
. The short-time Fourier transform (STFT), also called ( continuous ) Gabor transform of a function 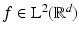 with respect to g, is defined as
with respect to g, is defined as
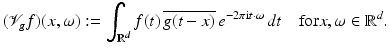
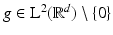 . The short-time Fourier transform (STFT), also called ( continuous ) Gabor transform of a function
. The short-time Fourier transform (STFT), also called ( continuous ) Gabor transform of a function 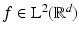 with respect to g, is defined as
with respect to g, is defined as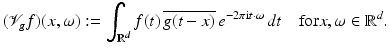
(29)
For 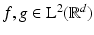 , the STFT
, the STFT 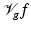 is uniformly continuous (by Riemann–Lebesgue) on
is uniformly continuous (by Riemann–Lebesgue) on 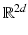 and can be written as
and can be written as
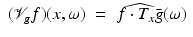
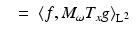
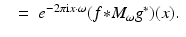
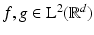 , the STFT
, the STFT 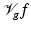 is uniformly continuous (by Riemann–Lebesgue) on
is uniformly continuous (by Riemann–Lebesgue) on 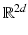 and can be written as
and can be written as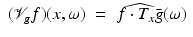
(30)
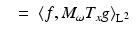
(31)
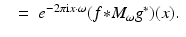
(32)
The STFT as a function in x and ω seems to provide the possibility to obtain information about the occurrence of arbitrary frequencies ω at arbitrary locations x as desired. However, the uncertainty principle (cf. [51]) implies that there is a limitation concerning the joint resolution. In fact, the STFT has limitations in its time–frequency resolution capability: Low frequencies can hardly be located with narrow windows, and similarly, short pulses remain invisible for wide windows. The choice of the analyzing window is therefore crucial.
Just like the Fourier transform, the STFT is a kind of time–frequency representation of a signal. This again raises the question of how to reconstruct the signal from its time–frequency representation. To approach this, we need the orthogonality relations of the STFT, which corresponds to Parseval’s formula (20) for the Fourier transform:
Theorem 7 (Orthogonality relations for STFT).
Let 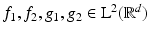 . Then
. Then 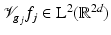 for j ∈{ 1,2}, and
for j ∈{ 1,2}, and
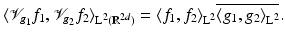
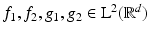 . Then
. Then 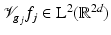 for j ∈{ 1,2}, and
for j ∈{ 1,2}, and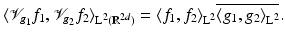
Corollary 3.
If 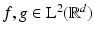 , then
, then
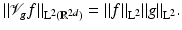 In the case of
In the case of 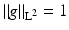 , we have
, we have
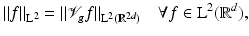
i.e., the STFT as an isometry from 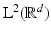 into
into 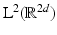 .
.
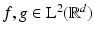 , then
, then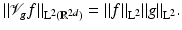
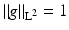 , we have
, we have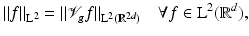
(33)
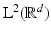 into
into 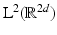 .
.Formula (33) shows that the STFT preserves the energy of a signal; it corresponds to (19) which shows the same property for the Fourier transform. Therefore, f is completely determined by 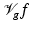 , and the inversion is given by a vector-valued integral (for good functions valid in the pointwise sense):
, and the inversion is given by a vector-valued integral (for good functions valid in the pointwise sense):
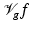 , and the inversion is given by a vector-valued integral (for good functions valid in the pointwise sense):
, and the inversion is given by a vector-valued integral (for good functions valid in the pointwise sense):Corollary 4 (Inversion formula for the STFT).
Let 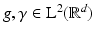 and
and 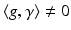 . Then
. Then
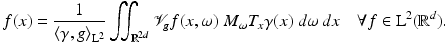
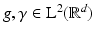 and
and 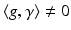 . Then
. Then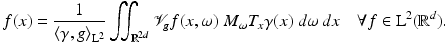
(34)
Obviously, γ = g is a natural choice here. The time–frequency analysis of signals is usually done by three subsequent steps:
(i)
Analysis: Using the STFT, the signal is transformed into a joint time–frequency representation.
(ii)
Processing: The obtained signal representation is then manipulated in a certain way, e.g., by restriction to a part of the signal yielding the relevant information.
(iii)
Synthesis: The inverse STFT is applied to the processed representation, thus creating a new signal.
A function is completely represented by its STFT but in a highly redundant way. To minimize the influence of the uncertainty principle, the analyzing window g should be chosen such that g and its Fourier transform 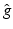 both decay rapidly, e.g., as Schwartz functions. A computational implementation can only be obtained by a discretization of both the functions and the STFT. Therefore, only sampled versions of the STFT are possible, and only certain locations and frequencies are used for analyzing a given signal. The challenge is to find the appropriate lattice constants in time and frequency and to obtain good time–frequency resolution.
both decay rapidly, e.g., as Schwartz functions. A computational implementation can only be obtained by a discretization of both the functions and the STFT. Therefore, only sampled versions of the STFT are possible, and only certain locations and frequencies are used for analyzing a given signal. The challenge is to find the appropriate lattice constants in time and frequency and to obtain good time–frequency resolution.
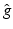 both decay rapidly, e.g., as Schwartz functions. A computational implementation can only be obtained by a discretization of both the functions and the STFT. Therefore, only sampled versions of the STFT are possible, and only certain locations and frequencies are used for analyzing a given signal. The challenge is to find the appropriate lattice constants in time and frequency and to obtain good time–frequency resolution.
both decay rapidly, e.g., as Schwartz functions. A computational implementation can only be obtained by a discretization of both the functions and the STFT. Therefore, only sampled versions of the STFT are possible, and only certain locations and frequencies are used for analyzing a given signal. The challenge is to find the appropriate lattice constants in time and frequency and to obtain good time–frequency resolution. 4 Gabor Frames in L2(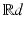 )
)
By formula (31), the STFT analyzes a function 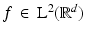 into coefficients
into coefficients 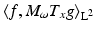 using modulations and translations of a single window function
using modulations and translations of a single window function 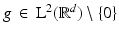 . One problem we noticed was that these TF-shifts are infinitesimal and overlap largely, making the STFT a highly redundant time–frequency representation. An idea to overcome this is to restrict to discrete choices of time positions x and frequencies ω such that this redundancy is decreased while leaving enough information in the coefficients about the time–frequency behavior of f. This is the very essence of Gabor analysis: It is sought to expand functions in
. One problem we noticed was that these TF-shifts are infinitesimal and overlap largely, making the STFT a highly redundant time–frequency representation. An idea to overcome this is to restrict to discrete choices of time positions x and frequencies ω such that this redundancy is decreased while leaving enough information in the coefficients about the time–frequency behavior of f. This is the very essence of Gabor analysis: It is sought to expand functions in 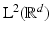 into an absolutely convergent series of modulations and translations of a window function g. Therefore, it is interesting to find necessary and sufficient conditions on g and a discrete set
into an absolutely convergent series of modulations and translations of a window function g. Therefore, it is interesting to find necessary and sufficient conditions on g and a discrete set 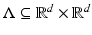 such that
such that
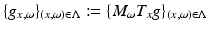 forms a frame for
forms a frame for 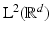 . The question arises how the sampling set
. The question arises how the sampling set 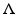 should be structured. It turns out to be very convenient to have this set closed under the addition operation, urging
should be structured. It turns out to be very convenient to have this set closed under the addition operation, urging 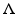 to be a subgroup of the time–frequency plane, i.e.,
to be a subgroup of the time–frequency plane, i.e., 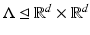 . Dennis Gabor (actually Dénes Gábor) suggested in his Theory of Communication [45], 1946, to use fixed step sizes α, β > 0 for time and frequency and use the set
. Dennis Gabor (actually Dénes Gábor) suggested in his Theory of Communication [45], 1946, to use fixed step sizes α, β > 0 for time and frequency and use the set 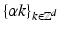 for the time positions and
for the time positions and 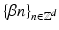 for the frequencies, yielding the functions
for the frequencies, yielding the functions
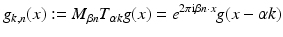 as analyzing elements. This is the approach that is usually presented in the literature, although there is also a more general group theoretical setting possible where
as analyzing elements. This is the approach that is usually presented in the literature, although there is also a more general group theoretical setting possible where 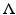 is an arbitrary (discrete) subgroup. This subgroup is also called a time–frequency lattice , although it does not have to be of such a “rectangular” shape in general.
is an arbitrary (discrete) subgroup. This subgroup is also called a time–frequency lattice , although it does not have to be of such a “rectangular” shape in general.
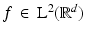 into coefficients
into coefficients 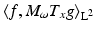 using modulations and translations of a single window function
using modulations and translations of a single window function 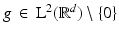 . One problem we noticed was that these TF-shifts are infinitesimal and overlap largely, making the STFT a highly redundant time–frequency representation. An idea to overcome this is to restrict to discrete choices of time positions x and frequencies ω such that this redundancy is decreased while leaving enough information in the coefficients about the time–frequency behavior of f. This is the very essence of Gabor analysis: It is sought to expand functions in
. One problem we noticed was that these TF-shifts are infinitesimal and overlap largely, making the STFT a highly redundant time–frequency representation. An idea to overcome this is to restrict to discrete choices of time positions x and frequencies ω such that this redundancy is decreased while leaving enough information in the coefficients about the time–frequency behavior of f. This is the very essence of Gabor analysis: It is sought to expand functions in 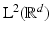 into an absolutely convergent series of modulations and translations of a window function g. Therefore, it is interesting to find necessary and sufficient conditions on g and a discrete set
into an absolutely convergent series of modulations and translations of a window function g. Therefore, it is interesting to find necessary and sufficient conditions on g and a discrete set 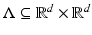 such that
such that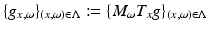
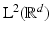 . The question arises how the sampling set
. The question arises how the sampling set 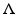 should be structured. It turns out to be very convenient to have this set closed under the addition operation, urging
should be structured. It turns out to be very convenient to have this set closed under the addition operation, urging 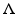 to be a subgroup of the time–frequency plane, i.e.,
to be a subgroup of the time–frequency plane, i.e., 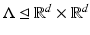 . Dennis Gabor (actually Dénes Gábor) suggested in his Theory of Communication [45], 1946, to use fixed step sizes α, β > 0 for time and frequency and use the set
. Dennis Gabor (actually Dénes Gábor) suggested in his Theory of Communication [45], 1946, to use fixed step sizes α, β > 0 for time and frequency and use the set 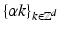 for the time positions and
for the time positions and 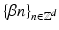 for the frequencies, yielding the functions
for the frequencies, yielding the functions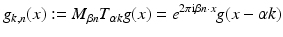
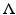 is an arbitrary (discrete) subgroup. This subgroup is also called a time–frequency lattice , although it does not have to be of such a “rectangular” shape in general.
is an arbitrary (discrete) subgroup. This subgroup is also called a time–frequency lattice , although it does not have to be of such a “rectangular” shape in general.Definition 10.
A lattice 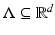 is a (discrete) subgroup of
is a (discrete) subgroup of 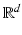 of the form
of the form 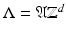 , where
, where 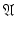 is an invertible
is an invertible 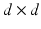 -matrix over
-matrix over 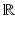 . Lattices in
. Lattices in 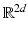 can be described as
can be described as
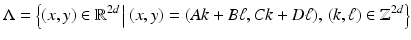 with
with 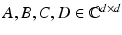 and
and
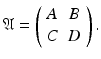 A lattice
A lattice 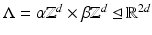 for α, β > 0 is called a separable lattice, a product lattice, or a grid.
for α, β > 0 is called a separable lattice, a product lattice, or a grid.
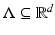 is a (discrete) subgroup of
is a (discrete) subgroup of 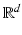 of the form
of the form 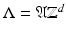 , where
, where 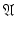 is an invertible
is an invertible 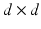 -matrix over
-matrix over 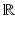 . Lattices in
. Lattices in 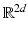 can be described as
can be described as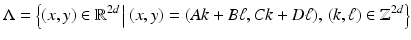
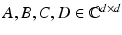 and
and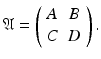
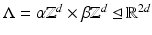 for α, β > 0 is called a separable lattice, a product lattice, or a grid.
for α, β > 0 is called a separable lattice, a product lattice, or a grid.In the following, our lattice will be of the separable type for fixed lattice parameters α, β > 0.
Definition 11.
For a nonzero window function 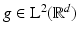 and lattice parameters α, β > 0, the set of time–frequency shifts
and lattice parameters α, β > 0, the set of time–frequency shifts
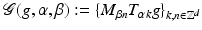 is called a Gabor system. If
is called a Gabor system. If 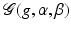 is a frame for
is a frame for 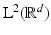 , it is called a Gabor frame or Weyl–Heisenberg frame . The associated frame operator is the Gabor frame operator and takes the form
, it is called a Gabor frame or Weyl–Heisenberg frame . The associated frame operator is the Gabor frame operator and takes the form
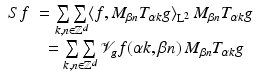
for all 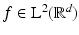 . The window g is also called the Gabor atom .
. The window g is also called the Gabor atom .
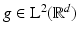 and lattice parameters α, β > 0, the set of time–frequency shifts
and lattice parameters α, β > 0, the set of time–frequency shifts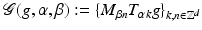
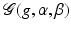 is a frame for
is a frame for 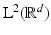 , it is called a Gabor frame or Weyl–Heisenberg frame . The associated frame operator is the Gabor frame operator and takes the form
, it is called a Gabor frame or Weyl–Heisenberg frame . The associated frame operator is the Gabor frame operator and takes the form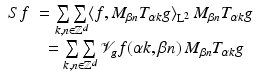
(35)
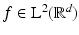 . The window g is also called the Gabor atom .
. The window g is also called the Gabor atom .According to the general frame theory, 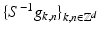 yields the canonical dual frame. So we would have to compute S −1 and apply it to all modulated and translated versions of the Gabor atom g. A direct computation shows that for arbitrary fixed indices
yields the canonical dual frame. So we would have to compute S −1 and apply it to all modulated and translated versions of the Gabor atom g. A direct computation shows that for arbitrary fixed indices 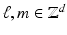 ,
,
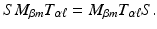
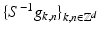 yields the canonical dual frame. So we would have to compute S −1 and apply it to all modulated and translated versions of the Gabor atom g. A direct computation shows that for arbitrary fixed indices
yields the canonical dual frame. So we would have to compute S −1 and apply it to all modulated and translated versions of the Gabor atom g. A direct computation shows that for arbitrary fixed indices 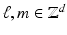 ,
,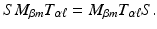
(36)
Consequently, also S −1 commutes with time–frequency shifts, which gives the following fundamental result for (regular) Gabor analysis:
Theorem 8.
If the given Gabor system 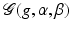 is a frame for
is a frame for 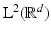 , then all of the following hold:
, then all of the following hold:
Get Clinical Tree app for offline access
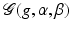 is a frame for
is a frame for 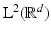 , then all of the following hold:
, then all of the following hold:(a)
There exists a dual window 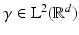 such that the dual frame is given by the Gabor frame
such that the dual frame is given by the Gabor frame 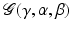 .
.
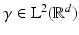 such that the dual frame is given by the Gabor frame
such that the dual frame is given by the Gabor frame 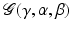 .
.(b)
Every 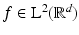 has an expansion of the form
has an expansion of the form
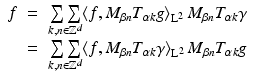




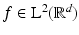 has an expansion of the form
has an expansion of the form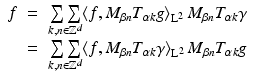
(37)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree