(1)
Here, t + m denotes the one-sided power function, i.e., t + m = 0 for t < 0 and t + m = t m for t ≥ 0. The B-splines β m can be easily generated by an iterative process. Let β 0(t) = χ [0, 1)(t) be the characteristic function of the interval [0, 1). Then the B-spline of degree m is derived by the convolution product
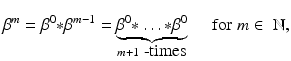
(2)
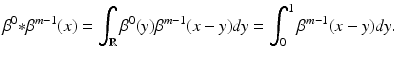
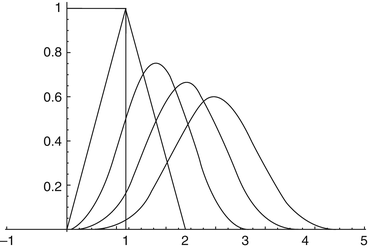
Fig. 1
Cardinal B-splines of degree m = 0, …, 4
Splines had their second breakthrough as Battle [4] and Lemarié [38] discovered that B-splines generate multiresolution analyses . The simple form of the B-splines and their compact support, in particular, were convenient for designing multiresolution algorithms and fast implementations.
Definition 1.
Let 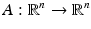 be a linear mapping that leaves
be a linear mapping that leaves 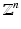 invariant, i.e.,
invariant, i.e., 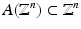 and that has (real or complex) eigenvalues with absolute values greater than 1.
and that has (real or complex) eigenvalues with absolute values greater than 1.
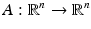 be a linear mapping that leaves
be a linear mapping that leaves 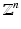 invariant, i.e.,
invariant, i.e., 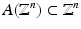 and that has (real or complex) eigenvalues with absolute values greater than 1.
and that has (real or complex) eigenvalues with absolute values greater than 1.A multiresolution analysis associated with the dilation matrix A is a sequence of nested subspaces 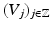 of
of 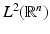 such that the following conditions hold:
such that the following conditions hold:
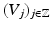 of
of 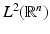 such that the following conditions hold:
such that the following conditions hold:(i)
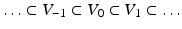 ,
,
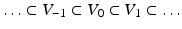 ,
,(ii)
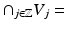 {0},
{0},
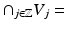 {0},
{0},(iii)
Span 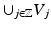 is dense in L2(
is dense in L2(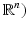 ,
,
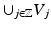 is dense in L2(
is dense in L2(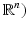 ,
,(iv)
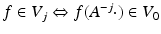 ,
,
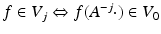 ,
,(v)
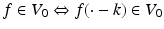 for all
for all 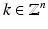 .
.
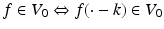 for all
for all 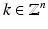 .
.(vi)
There exists a so-called scaling function ϕ ∈ V 0 such that the family 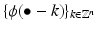 of translates of ϕ forms a Riesz basis of V 0.
of translates of ϕ forms a Riesz basis of V 0.
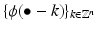 of translates of ϕ forms a Riesz basis of V 0.
of translates of ϕ forms a Riesz basis of V 0.Here, 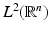 denotes the vector space of square-integrable functions f:
denotes the vector space of square-integrable functions f: 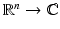 with norm
with norm
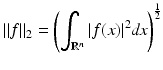 and corresponding inner product
and corresponding inner product
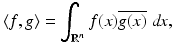 where
where 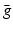 denotes the complex conjugate of g. The elements in
denotes the complex conjugate of g. The elements in 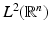 are also called functions of finite energy.
are also called functions of finite energy.
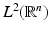 denotes the vector space of square-integrable functions f:
denotes the vector space of square-integrable functions f: 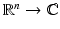 with norm
with norm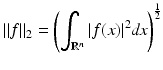
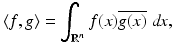
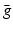 denotes the complex conjugate of g. The elements in
denotes the complex conjugate of g. The elements in 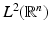 are also called functions of finite energy.
are also called functions of finite energy.Riesz bases are a slightly more general concept than orthonormal bases. In fact, Riesz bases are equivalent to orthonormal bases and therefore can be generated by applying a topological isomorphism on some orthonormal basis.
Definition 2.
A sequence of functions{f n }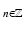 in a Hilbert space V is called a Riesz sequence if there exist positive constants A and B, the Riesz bounds, such that
in a Hilbert space V is called a Riesz sequence if there exist positive constants A and B, the Riesz bounds, such that
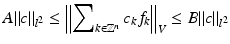 for all scalar sequences
for all scalar sequences 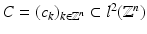 .
.
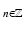 in a Hilbert space V is called a Riesz sequence if there exist positive constants A and B, the Riesz bounds, such that
in a Hilbert space V is called a Riesz sequence if there exist positive constants A and B, the Riesz bounds, such that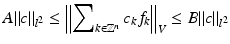
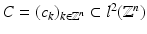 .
.A Riesz sequence is called a Riesz basis if it additionally spans the space V.
A good introduction to Riesz bases, their properties, and their relation to orthonormal bases is given in the monography by Young [75]. Multiresolution constructions with splines are treated in numerous sources. As a starting point, there are, e.g., the books by Christensen [13, 14] and Wojtaszczyk [74].
The mathematical properties in Definition 1 have intuitive interpretations. A function 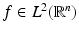 , which is projected orthogonally on V j , is approximated with the so-called resolution A j . In fact, let
, which is projected orthogonally on V j , is approximated with the so-called resolution A j . In fact, let
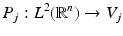 denote the orthogonal projection operator. Then (ii) yields that by going to lower resolutions, all details are lost:
denote the orthogonal projection operator. Then (ii) yields that by going to lower resolutions, all details are lost:
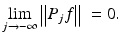 In contrast, when the resolution is increased, j → ∞, more and more details are added. By (iii), the projection then converges to the original function f:
In contrast, when the resolution is increased, j → ∞, more and more details are added. By (iii), the projection then converges to the original function f:
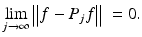 Hereby, the rate of convergence depends on the regularity of f.
Hereby, the rate of convergence depends on the regularity of f.
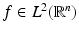 , which is projected orthogonally on V j , is approximated with the so-called resolution A j . In fact, let
, which is projected orthogonally on V j , is approximated with the so-called resolution A j . In fact, let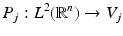
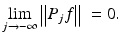
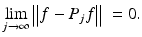
The approximation spaces V j are nested, which allows for computing coarser approximations in V k for k < j for functions f ∈ V j . The scaling A k enlarges details. Property (iv) shows that the approximation spaces have a similar structure over the scales and emanate from one another. The translation invariance (v) ensures that the analysis of a function in V j is independent of the starting time or location.
And property (vi) finally ensures the beautiful and mighty property that the whole sequence of nested approximation spaces can be generated by translates and scalings of one single function – the scaling function .In fact, (vi) together with (iv) yields that
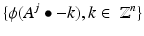 is a Riesz basis for V j .
is a Riesz basis for V j .
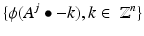
While moving from the coarser approximation space V j to the finer, larger space V j+1, information has to be added. In fact, there is an orthogonal complement W j , 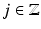 , such that
, such that
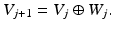 These spaces are called detail spaces or wavelet spaces. It is well known that these spaces also possess a Riesz basis spanned by shifts of
These spaces are called detail spaces or wavelet spaces. It is well known that these spaces also possess a Riesz basis spanned by shifts of 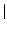 detA | − 1 generators, the wavelets ψ 1, …, ψ | detA | −1. Here, A is the dilation matrix in Definition 1. The wavelets can be constructed from the scaling function. As a consequence, the knowledge of just the single function ϕ allows for the construction of the approximation spaces V j and for the wavelet spaces W j . Detailed information on the generation of wavelets and their properties can be found in various books, e.g., [16, 21, 41, 44, 74].
detA | − 1 generators, the wavelets ψ 1, …, ψ | detA | −1. Here, A is the dilation matrix in Definition 1. The wavelets can be constructed from the scaling function. As a consequence, the knowledge of just the single function ϕ allows for the construction of the approximation spaces V j and for the wavelet spaces W j . Detailed information on the generation of wavelets and their properties can be found in various books, e.g., [16, 21, 41, 44, 74].
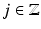 , such that
, such that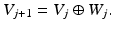
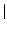 detA | − 1 generators, the wavelets ψ 1, …, ψ | detA | −1. Here, A is the dilation matrix in Definition 1. The wavelets can be constructed from the scaling function. As a consequence, the knowledge of just the single function ϕ allows for the construction of the approximation spaces V j and for the wavelet spaces W j . Detailed information on the generation of wavelets and their properties can be found in various books, e.g., [16, 21, 41, 44, 74].
detA | − 1 generators, the wavelets ψ 1, …, ψ | detA | −1. Here, A is the dilation matrix in Definition 1. The wavelets can be constructed from the scaling function. As a consequence, the knowledge of just the single function ϕ allows for the construction of the approximation spaces V j and for the wavelet spaces W j . Detailed information on the generation of wavelets and their properties can be found in various books, e.g., [16, 21, 41, 44, 74].Example 1.
A simple example for a multiresolution analysis on 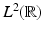 is given by piecewise constant functions. Consider the characteristic function ϕ = χ [0, 1) of the interval semi-open interval [0, 1). Then ϕ generates a dyadic multiresolution analysis, i.e., for A = 2. The approximation spaces are
is given by piecewise constant functions. Consider the characteristic function ϕ = χ [0, 1) of the interval semi-open interval [0, 1). Then ϕ generates a dyadic multiresolution analysis, i.e., for A = 2. The approximation spaces are
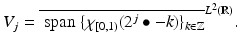 They consist of functions constant on intervals of the form [k2−j , (k + 1)2−j ). The spaces are obviously nested and separate
They consist of functions constant on intervals of the form [k2−j , (k + 1)2−j ). The spaces are obviously nested and separate  in the sense of Definition 1 (ii). Since piecewise constant functions with compact support are dense in
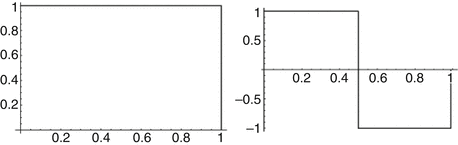
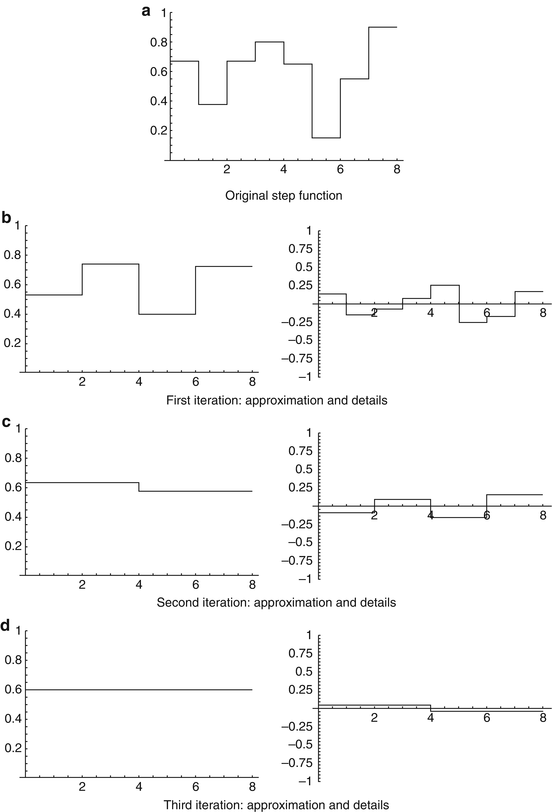
in the sense of Definition 1 (ii). Since piecewise constant functions with compact support are dense in  , (iii) holds. (iv) – (vi) hold by construction. In fact, this multiresolution analysis is generated by the B-spline β 0 as scaling function. The B-spline basis operates as mean-value operator over the support interval. The corresponding wavelet extracts the details, i.e., the deviation from the mean value. To this end, it operates as a difference operator. Figure 2 shows the scaling function β 0 and the corresponding wavelet, the so-called Haar wavelet. In Fig. 3, an example of a multiresolution is given.
, (iii) holds. (iv) – (vi) hold by construction. In fact, this multiresolution analysis is generated by the B-spline β 0 as scaling function. The B-spline basis operates as mean-value operator over the support interval. The corresponding wavelet extracts the details, i.e., the deviation from the mean value. To this end, it operates as a difference operator. Figure 2 shows the scaling function β 0 and the corresponding wavelet, the so-called Haar wavelet. In Fig. 3, an example of a multiresolution is given.
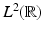 is given by piecewise constant functions. Consider the characteristic function ϕ = χ [0, 1) of the interval semi-open interval [0, 1). Then ϕ generates a dyadic multiresolution analysis, i.e., for A = 2. The approximation spaces are
is given by piecewise constant functions. Consider the characteristic function ϕ = χ [0, 1) of the interval semi-open interval [0, 1). Then ϕ generates a dyadic multiresolution analysis, i.e., for A = 2. The approximation spaces are
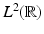 in the sense of Definition 1 (ii). Since piecewise constant functions with compact support are dense in
in the sense of Definition 1 (ii). Since piecewise constant functions with compact support are dense in 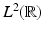 , (iii) holds. (iv) – (vi) hold by construction. In fact, this multiresolution analysis is generated by the B-spline β 0 as scaling function. The B-spline basis operates as mean-value operator over the support interval. The corresponding wavelet extracts the details, i.e., the deviation from the mean value. To this end, it operates as a difference operator. Figure 2 shows the scaling function β 0 and the corresponding wavelet, the so-called Haar wavelet. In Fig. 3, an example of a multiresolution is given.
, (iii) holds. (iv) – (vi) hold by construction. In fact, this multiresolution analysis is generated by the B-spline β 0 as scaling function. The B-spline basis operates as mean-value operator over the support interval. The corresponding wavelet extracts the details, i.e., the deviation from the mean value. To this end, it operates as a difference operator. Figure 2 shows the scaling function β 0 and the corresponding wavelet, the so-called Haar wavelet. In Fig. 3, an example of a multiresolution is given.
Fig. 2
Left: The B-spline β 0 is a scaling function and operates as mean value. Right: The corresponding wavelet, the Haar wavelet, operates as a local difference operator

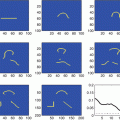
Fig. 3
Multiresolution decomposition of the step function (a) with β 0 as scaling function and with the Haar wavelet. The approximations (left column) are further iterated and decomposed into a coarser approximation and details (right column), until the coarsest approximation step, here the mean value, is reached. The sum of the coarsest approximation in the third iteration and of all details yields the original function (a). No information is lost in a multiresolution decomposition
2 Historical Notes
The idea of piecewise polynomial functions and splines goes back to Schoenberg [59, 60]. In the 1960s, when computer power started to be used for numerical procedures such as data fitting, interpolation, solving differential equations, and computer-aided geometric design, splines experienced an extreme upsurge. Schoenberg invented and strongly contributed to the concept of cardinal splines, which have equidistant nodes on the integers; see, e.g., [40, 61, 62] and many more.
As a parallel development, in the 1980s, the adaption of signal resolution to only process relevant details for a particular task evolved. For example, for computer vision, a multiresolution pyramid was introduced by Burt and Adelson [8]. It allowed to process an image first on a low-resolution level and then selectively increase the resolution and add more detailed information when needed. The definition of a dyadic multiresolution analysis , i.e., A = 2Id, was contributed by Mallat [43] and Meyer [46]. An interesting and in some parts historical collection on the most important articles in multiresolution and wavelet theory was assembled by Heil and Walnut [33].
The concepts of splines and multiresolution were joined by Lemarié [38] and Battle [4], when they showed that cardinal B-splines are scaling functions for multiresolution analyses. This led to many more developments of piecewise polynomial scaling functions for various settings and also multidimensions [15], as, e.g., polyharmonic B-splines [53, 54] and other functions inspired from radial basis functions [7].
In 1989, S. Mallat published his famous algorithm for multiresolution and wavelet analysis [43]. He had developed an efficient numerical method such that multiresolution decompositions could be calculated in a fast way. For the splines, M. Unser et al. proposed a fast implementation [66, 68, 69] which strongly contributed to the breakthrough of splines for signal and image analysis. In the last years, periodic, fractional, and complex versions of splines for multiresolution were developed, e.g., [11, 27, 28, 51, 65]. Many of them use a Fourier domain filter algorithm which allows for infinite impulse response filters. The former important feature of compact support of the cardinal B-splines and other functions is no longer a limiting criterion. Therefore, it can be expected that many new contributions on splines will still be made in the future by modeling signal and image features in Fourier domain.
3 Fourier Transform, Multiresolution, Splines, and Wavelets
Mathematical Foundations
Regularity and Decay Under the Fourier Transform
An important idea behind splines and multiresolution is the relation between regularity in time domain and decay in frequency domain and, respectively, between decay in time domain and regularity in frequency domain. To illustrate this, the notion of the Schwartz space is very useful [10, 34, 56, 63].
Definition 3.
The subspace of functions 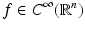 with
with
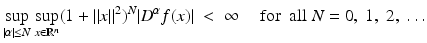 is called the space of rapidly decreasing functions or Schwartz space
is called the space of rapidly decreasing functions or Schwartz space 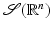 . The norms induce a Fréchet space topology, i.e., the space
. The norms induce a Fréchet space topology, i.e., the space 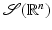 is complete and metrizable.
is complete and metrizable.
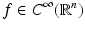 with
with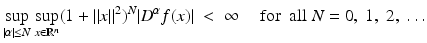
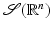 . The norms induce a Fréchet space topology, i.e., the space
. The norms induce a Fréchet space topology, i.e., the space 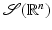 is complete and metrizable.
is complete and metrizable.Here, 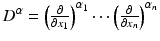 for every multi-index
for every multi-index 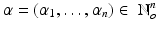 .
.
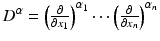 for every multi-index
for every multi-index 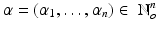 .
.The dual space 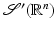 , endowed with the weak-* topology, is called space of tempered distributions.
, endowed with the weak-* topology, is called space of tempered distributions.
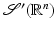 , endowed with the weak-* topology, is called space of tempered distributions.
, endowed with the weak-* topology, is called space of tempered distributions.The following famous linear transform relates the viewpoints of the space domain and of the frequency domain:
Definition 4.
The Fourier transform, defined by
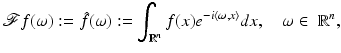 is a topological isomorphism on
is a topological isomorphism on 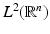 and on
and on 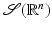 . Its inverse is given by
. Its inverse is given by
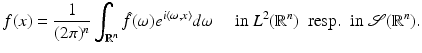 The Fourier transform can be extended to the space of tempered distributions. For
The Fourier transform can be extended to the space of tempered distributions. For 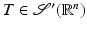 , the Fourier transform is defined in a weak sense as
, the Fourier transform is defined in a weak sense as
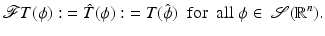 Also on
Also on 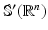 , the Fourier transform is a topological isomorphism.
, the Fourier transform is a topological isomorphism.
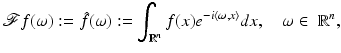
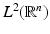 and on
and on 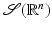 . Its inverse is given by
. Its inverse is given by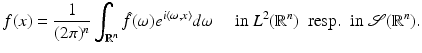
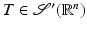 , the Fourier transform is defined in a weak sense as
, the Fourier transform is defined in a weak sense as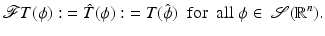
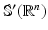 , the Fourier transform is a topological isomorphism.
, the Fourier transform is a topological isomorphism.The Fourier transform has the nice property to relate polynomials and differential operators.
Theorem 1.
(i)
Let 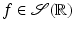 . Then for all
. Then for all 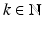
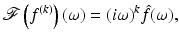 and
and
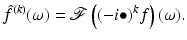
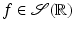 . Then for all
. Then for all 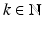
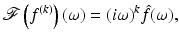
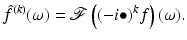
(ii)
Let P be an algebraic polynomial in 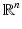 , say
, say 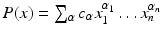 , and let
, and let 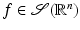 . Then
. Then
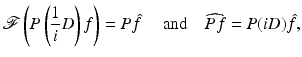 where
where 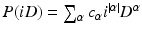 .
.
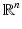 , say
, say 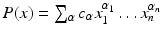 , and let
, and let 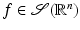 . Then
. Then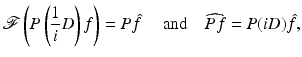
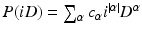 .
.(iii)
Part (ii) also holds for 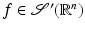 .
.
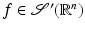 .
.Example 2.
The Fourier transform of the polynomial x k is the tempered distribution 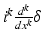 ,
, 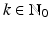 .
.
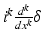 ,
, 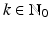 .
.For the construction of a multiresolution analysis, the scaling function can be used as a starting point. The idea is to choose a scaling function of a certain regularity, such that the generated multiresolution analysis inherits the smoothness properties. In particular, for the splines, the idea is to model the regularity via decay in Fourier domain. The following theorem gives a motivation for this. The result can be deduced from the considerations above, and the fact that 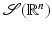 is dense in
is dense in 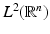 :
:
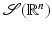 is dense in
is dense in 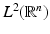 :
:Theorem 2.
Let 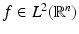 and its Fourier-transform decay as
and its Fourier-transform decay as
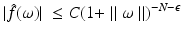 for some
for some ![$$\varepsilon > 0$$” src=”/wp-content/uploads/2016/04/A183156_2_En_28_Chapter_IEq48.gif”></SPAN>. <SPAN class=EmphasisTypeItalic>Then all partial derivatives of order ≤N − n are continuous and in</SPAN> <SPAN id=IEq49 class=InlineEquation><IMG alt=$$L^{2}(\mathbb{R}^{n})$$ src=]() .
.
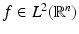 and its Fourier-transform decay as
and its Fourier-transform decay as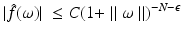
These results allow to construct a scaling function with explicit regularity and decay properties, in space and in frequency domain. However, some criteria are needed to verify that the constructed function generates a multiresolution analysis.
Criteria for Riesz Sequences and Multiresolution Analyses
The following is an explicit criterion to verify whether some function ϕ is a scaling function.
Theorem 3.
Let A be a dilation matrix and let 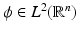 be some function satisfying the following properties:
be some function satisfying the following properties:
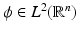 be some function satisfying the following properties:
be some function satisfying the following properties:(i)
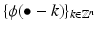 is a Riesz sequence in
is a Riesz sequence in 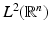 .
.
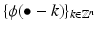 is a Riesz sequence in
is a Riesz sequence in 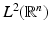 .
.(ii)
ϕ satisfies a scaling relation. That is, there is a sequence of coefficients 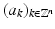 such that
such that
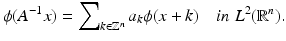
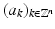 such that
such that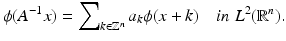
(3)
(iii)
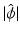 is continuous at 0 and
is continuous at 0 and 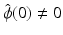 .
.
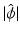 is continuous at 0 and
is continuous at 0 and 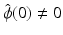 .
.Then the spaces
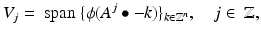 form a multiresolution analysis of
form a multiresolution analysis of 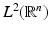 with respect to the dilation matrix A.
with respect to the dilation matrix A.
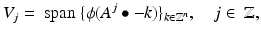
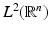 with respect to the dilation matrix A.
with respect to the dilation matrix A. Proof.
See, e.g., [74, Theorem 2.13] for the 1D case.
For particular applications, the Riesz basis property (i) of 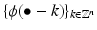 in V 0 is not enough, but an orthonormal basis is needed. An example for such an application is the denoising of signals contaminated with Gaussian white noise [44, Chap. X, Sect. 10.2.1]. However, there is an elegant mathematical method to orthonormalize Riesz bases generated by shifts of a single function.
in V 0 is not enough, but an orthonormal basis is needed. An example for such an application is the denoising of signals contaminated with Gaussian white noise [44, Chap. X, Sect. 10.2.1]. However, there is an elegant mathematical method to orthonormalize Riesz bases generated by shifts of a single function.
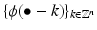 in V 0 is not enough, but an orthonormal basis is needed. An example for such an application is the denoising of signals contaminated with Gaussian white noise [44, Chap. X, Sect. 10.2.1]. However, there is an elegant mathematical method to orthonormalize Riesz bases generated by shifts of a single function.
in V 0 is not enough, but an orthonormal basis is needed. An example for such an application is the denoising of signals contaminated with Gaussian white noise [44, Chap. X, Sect. 10.2.1]. However, there is an elegant mathematical method to orthonormalize Riesz bases generated by shifts of a single function.Theorem 4.
Let 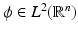 . Then the following holds:
. Then the following holds:
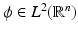 . Then the following holds:
. Then the following holds:(i)
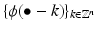 is a Riesz sequence in
is a Riesz sequence in 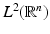 if and only if there are constants c and C, such that
if and only if there are constants c and C, such that
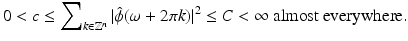 That is, the autocorrelation filter
That is, the autocorrelation filter 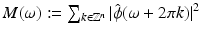 is strictly positive and bounded from above.
is strictly positive and bounded from above.
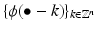 is a Riesz sequence in
is a Riesz sequence in 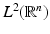 if and only if there are constants c and C, such that
if and only if there are constants c and C, such that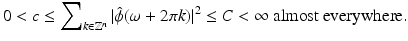
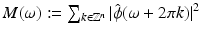 is strictly positive and bounded from above.
is strictly positive and bounded from above. (ii)
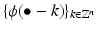 is an orthonormal sequence if and only if
is an orthonormal sequence if and only if
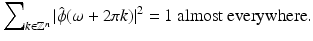
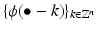 is an orthonormal sequence if and only if
is an orthonormal sequence if and only if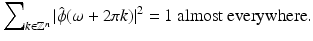
(iii)
If 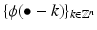 is a Riesz basis of a subspace X of
is a Riesz basis of a subspace X of 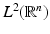 , then there exists a function
, then there exists a function 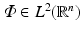 , namely,
, namely,
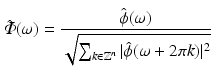
such that 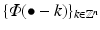 is an orthonormal basis of X.
is an orthonormal basis of X.
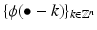 is a Riesz basis of a subspace X of
is a Riesz basis of a subspace X of 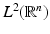 , then there exists a function
, then there exists a function 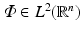 , namely,
, namely,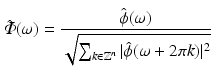
(4)
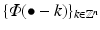 is an orthonormal basis of X.
is an orthonormal basis of X. Proof.
Due to this theorem, every scaling function can be orthonormalized. Let 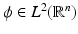 be some scaling function that generates a multiresolution analysis {V j }
be some scaling function that generates a multiresolution analysis {V j } of
of 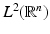 . Then the family
. Then the family 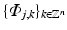 with
with
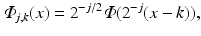 and Φ as defined in (4) is an orthonormal basis of the space
and Φ as defined in (4) is an orthonormal basis of the space 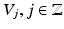 .
.
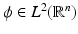 be some scaling function that generates a multiresolution analysis {V j }
be some scaling function that generates a multiresolution analysis {V j } of
of  . Then the family
. Then the family  with
with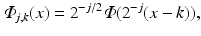
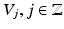 .
.Example 3.
A simple possibility to construct a dyadic multiresolution analysis in 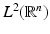 is the tensor product approach. Let
is the tensor product approach. Let 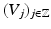 be a dyadic (i.e., A = 2) multiresolution analysis of
be a dyadic (i.e., A = 2) multiresolution analysis of 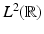 with scaling function ϕ. Then (
with scaling function ϕ. Then (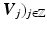 with
with 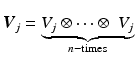 together with the scaling function
together with the scaling function 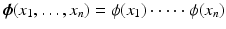 forms a multiresolution analysis of
forms a multiresolution analysis of 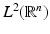 and dilation matrix 2Id.
and dilation matrix 2Id.
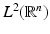 is the tensor product approach. Let
is the tensor product approach. Let 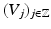 be a dyadic (i.e., A = 2) multiresolution analysis of
be a dyadic (i.e., A = 2) multiresolution analysis of 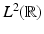 with scaling function ϕ. Then (
with scaling function ϕ. Then (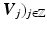 with
with 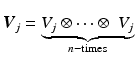 together with the scaling function
together with the scaling function 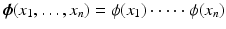 forms a multiresolution analysis of
forms a multiresolution analysis of 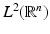 and dilation matrix 2Id.
and dilation matrix 2Id.In the same way, the scaling function 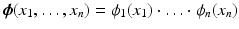 generates a multiresolution analysis of
generates a multiresolution analysis of 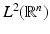 , if every
, if every 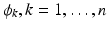 , is a scaling function of some 1D multiresolution analysis with dilation factor
, is a scaling function of some 1D multiresolution analysis with dilation factor 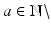 {1}.
{1}.
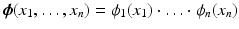 generates a multiresolution analysis of
generates a multiresolution analysis of 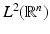 , if every
, if every 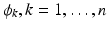 , is a scaling function of some 1D multiresolution analysis with dilation factor
, is a scaling function of some 1D multiresolution analysis with dilation factor 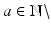 {1}.
{1}.Regularity of Multiresolution Analysis
In signal and image analysis, the choice of an appropriate analysis basis is crucial. Here, appropriate means that the features of the basis such as smoothness should be in accordance with the properties of the functions to analyze. To give a blatant example: Analyzing a smooth signal or image with a fractal basis in general yields results that are difficult to interpret and to work with in practice. In this case, the signal resp. the image model does not match the model of the basis.
The next section will show that the family of spline bases helps to avoid such difficulties, because the splines allow for a good adjustment due to their regularity parameter m; cf. (1) and (2). The following definition specifies the term “regular.” (See [74].)
Definition 5.
Denote C r the class of r-times continuously differentiable functions in 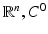 the class of continuous functions, and C −1 the class of measurable functions.
the class of continuous functions, and C −1 the class of measurable functions.
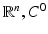 the class of continuous functions, and C −1 the class of measurable functions.
the class of continuous functions, and C −1 the class of measurable functions.(i)
Let r = −1, 0, 1, …. A function 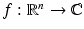 is called r-regular, iff ∈ C r and
is called r-regular, iff ∈ C r and
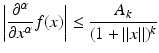 for every
for every 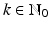 , every multi-index α with | α | ≤ max(r, 0) and constants A k .
, every multi-index α with | α | ≤ max(r, 0) and constants A k .
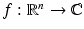 is called r-regular, iff ∈ C r and
is called r-regular, iff ∈ C r and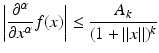
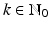 , every multi-index α with | α | ≤ max(r, 0) and constants A k .
, every multi-index α with | α | ≤ max(r, 0) and constants A k .(ii)
A multiresolution analysis of 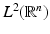 is called r-regular if it is generated by an r-regular scaling function.
is called r-regular if it is generated by an r-regular scaling function.
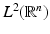 is called r-regular if it is generated by an r-regular scaling function.
is called r-regular if it is generated by an r-regular scaling function.It is important to note that the orthonormalization procedure (4) does not affect the regularity of the corresponding basis. For the orthonormalized scaling function Φ of a multiresolution analysis, the same regularity properties hold.
Proposition 1.
Let 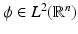 be an r-regular function, such that
be an r-regular function, such that 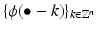 forms a Riesz sequence. Then the via (4) orthonormalized function Φ is also r-regular [ 74 ].
forms a Riesz sequence. Then the via (4) orthonormalized function Φ is also r-regular [ 74 ].
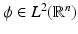 be an r-regular function, such that
be an r-regular function, such that 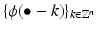 forms a Riesz sequence. Then the via (4) orthonormalized function Φ is also r-regular [ 74 ].
forms a Riesz sequence. Then the via (4) orthonormalized function Φ is also r-regular [ 74 ]. Order of Approximation
Having found a scaling function that generates a multiresolution analysis, how good do the corresponding approximation spaces V j approximate some function 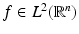 of a certain regularity? Let
of a certain regularity? Let
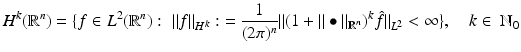 denote the Sobolev spaces. The following criterion for the order of approximation turns out to be easy to verify for splines.
denote the Sobolev spaces. The following criterion for the order of approximation turns out to be easy to verify for splines.
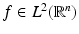 of a certain regularity? Let
of a certain regularity? Let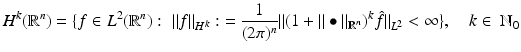
Theorem 5.
Let 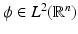 satisfy the following properties [23, Theorem 1.15]:
satisfy the following properties [23, Theorem 1.15]:
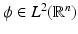 satisfy the following properties [23, Theorem 1.15]:
satisfy the following properties [23, Theorem 1.15]:(i)
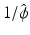 is bounded on some neighborhood of the origin.
is bounded on some neighborhood of the origin.
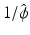 is bounded on some neighborhood of the origin.
is bounded on some neighborhood of the origin. (ii)
Let 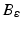 be some open ball centered at the origin and let E: =
be some open ball centered at the origin and let E: = 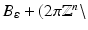 {0}). For some α > k + n∕2, all derivatives of
{0}). For some α > k + n∕2, all derivatives of 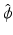 of order ≤α are in L 2 (E).
of order ≤α are in L 2 (E).
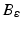 be some open ball centered at the origin and let E: =
be some open ball centered at the origin and let E: = 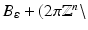 {0}). For some α > k + n∕2, all derivatives of
{0}). For some α > k + n∕2, all derivatives of 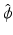 of order ≤α are in L 2 (E).
of order ≤α are in L 2 (E). (iii)
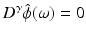 for all |γ| < k and all
for all |γ| < k and all 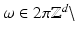 {0}.
{0}.
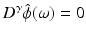 for all |γ| < k and all
for all |γ| < k and all 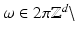 {0}.
{0}. Then 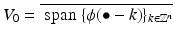 provides an approximation order k:
provides an approximation order k:
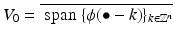 provides an approximation order k:
provides an approximation order k: For 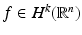 ,
,
![$$\displaystyle{\min \{\left \|f - s(\bullet /h)\right \|_{L^{2}},s \in V _{0}\} \leq \mbox{ const}.\;h^{k}\left \|f\right \|_{ H^{k}}\quad \mbox{ for}\;\mbox{ all}\;h > 0.}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_28_Chapter_Equy.gif”></DIV></DIV></DIV></DIV></DIV></DIV><br />
<DIV id=Sec9 class=]()
Get Clinical Tree app for offline access

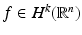 ,
,Wavelets
For the step from a coarser approximation space V j to a finer one V j+1, information has to be added. It is contained in the wavelet space or detail space W j , which is the orthonormal complement of V j in V j+1:
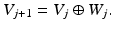 It follows that
It follows that 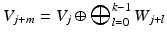 , and hence
, and hence
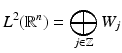
can be decomposed in a direct sum of mutually orthogonal detail spaces. Moreover, the detail spaces W j inherit the scaling property from Definition 1(iv) for the approximation spaces V j . For all 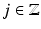 ,
,
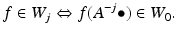 The question now is whether there is also a simple basis generated by the shifts of one or few functions, the wavelets. The following definition is motivated from Eq. (5).
The question now is whether there is also a simple basis generated by the shifts of one or few functions, the wavelets. The following definition is motivated from Eq. (5).
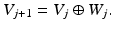
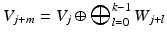 , and hence
, and hence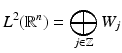
(5)
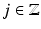 ,
,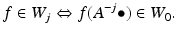
Definition 6.
Let A be a dilation matrix, and let {ψ l }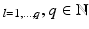 , be a set of functions in
, be a set of functions in 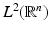 , such that the family
, such that the family
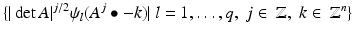 forms an orthonormal basis of
forms an orthonormal basis of 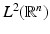 . Then {ψ l } l = 1, …, q is called a wavelet set associated with A.
. Then {ψ l } l = 1, …, q is called a wavelet set associated with A.
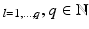 , be a set of functions in
, be a set of functions in 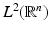 , such that the family
, such that the family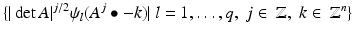
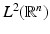 . Then {ψ l } l = 1, …, q is called a wavelet set associated with A.
. Then {ψ l } l = 1, …, q is called a wavelet set associated with A.What qualitative properties do the wavelets have? The approximation spaces V j are generated by the scaling function, which operates as a low-pass filter. This can be seen from Theorem 3(iii) 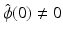 and resp. from Theorem 5(i):
and resp. from Theorem 5(i): 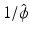 is bounded in some neighborhood of the origin. Therefore, the added details and thus the wavelets have to carry the high-frequency information. In addition, the wavelets ψ in W 0 are elements of V 1 and therefore have the form
is bounded in some neighborhood of the origin. Therefore, the added details and thus the wavelets have to carry the high-frequency information. In addition, the wavelets ψ in W 0 are elements of V 1 and therefore have the form
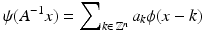
in L 2 norm, where 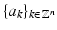 are the Fourier coefficients of a certain 2
are the Fourier coefficients of a certain 2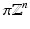 -periodic function.
-periodic function.
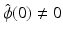 and resp. from Theorem 5(i):
and resp. from Theorem 5(i): 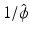 is bounded in some neighborhood of the origin. Therefore, the added details and thus the wavelets have to carry the high-frequency information. In addition, the wavelets ψ in W 0 are elements of V 1 and therefore have the form
is bounded in some neighborhood of the origin. Therefore, the added details and thus the wavelets have to carry the high-frequency information. In addition, the wavelets ψ in W 0 are elements of V 1 and therefore have the form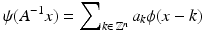
(6)
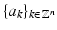 are the Fourier coefficients of a certain 2
are the Fourier coefficients of a certain 2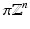 -periodic function.
-periodic function.Proposition 2.
Let 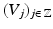 be a multiresolution analysis of
be a multiresolution analysis of 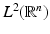 with respect to the dilation matrix A and with scaling function ϕ. Then for a function
with respect to the dilation matrix A and with scaling function ϕ. Then for a function 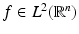 the following are equivalent: f ∈ V 1 id and only if
the following are equivalent: f ∈ V 1 id and only if
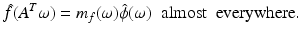 Here,
Here, ![$$m_{f} \in L^{2}([0,2\pi ]^{n})$$](/wp-content/uploads/2016/04/A183156_2_En_28_Chapter_IEq111.gif) and
and
![$$\displaystyle{\left \|m_{f}\right \|_{L^{2}([0,2\pi ]^{n})}^{2} = \frac{1} {\vert \det A\vert }\left \|f\right \|_{L^{2}(\mathbb{R}^{n})}^{2}.}$$](/wp-content/uploads/2016/04/A183156_2_En_28_Chapter_Equad.gif) For a proof, see, e.g., [21, 74]. Note that for a wavelet ψ as in Eq. (6), there holds
For a proof, see, e.g., [21, 74]. Note that for a wavelet ψ as in Eq. (6), there holds
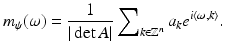 How many wavelets, i.e., generators of W 0, are needed to span the space? The parameter q in Definition 6 is yet unspecified. In fact, q depends on the scaling matrix. A leaves the lattice
How many wavelets, i.e., generators of W 0, are needed to span the space? The parameter q in Definition 6 is yet unspecified. In fact, q depends on the scaling matrix. A leaves the lattice 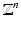 invariant, A
invariant, A 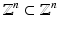 . The number of cosets is
. The number of cosets is 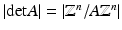 (see [74, Proposition 5.5]). It turns out that
(see [74, Proposition 5.5]). It turns out that  wavelets are needed to generate the space W 0. To motivate this, for a start, let f ∈ V 1 be an arbitrary function. Denote
wavelets are needed to generate the space W 0. To motivate this, for a start, let f ∈ V 1 be an arbitrary function. Denote 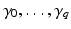 representatives of the q + 1 cosets of
representatives of the q + 1 cosets of 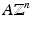 in
in 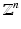 . Then each coset can be written as
. Then each coset can be written as 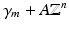 , m = 0,…,q. The function f has the representation
, m = 0,…,q. The function f has the representation
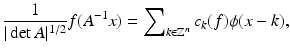
or in Fourier domain
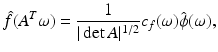
in L 2 sense and with an appropriate 2  -periodic function c f (ω) with Fourier coefficients
-periodic function c f (ω) with Fourier coefficients 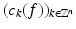 . Then
. Then 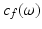 can be decomposed with respect to the cosets:
can be decomposed with respect to the cosets:
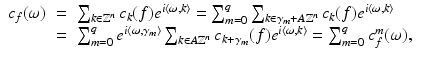 where
where
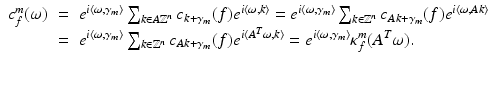 This representation exists for all functions V 1, in particular for ϕ and the wavelets. The following theorem indicates how the wavelets are constructed that generate the space W 0, such that W 0 ⊕ V 0 = V 1.
This representation exists for all functions V 1, in particular for ϕ and the wavelets. The following theorem indicates how the wavelets are constructed that generate the space W 0, such that W 0 ⊕ V 0 = V 1.
 be a multiresolution analysis of
be a multiresolution analysis of 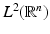 with respect to the dilation matrix A and with scaling function ϕ. Then for a function
with respect to the dilation matrix A and with scaling function ϕ. Then for a function 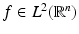 the following are equivalent: f ∈ V 1 id and only if
the following are equivalent: f ∈ V 1 id and only if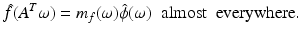
![$$m_{f} \in L^{2}([0,2\pi ]^{n})$$](/wp-content/uploads/2016/04/A183156_2_En_28_Chapter_IEq111.gif) and
and![$$\displaystyle{\left \|m_{f}\right \|_{L^{2}([0,2\pi ]^{n})}^{2} = \frac{1} {\vert \det A\vert }\left \|f\right \|_{L^{2}(\mathbb{R}^{n})}^{2}.}$$](/wp-content/uploads/2016/04/A183156_2_En_28_Chapter_Equad.gif)
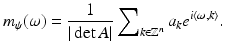
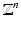 invariant, A
invariant, A 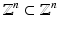 . The number of cosets is
. The number of cosets is 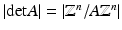 (see [74, Proposition 5.5]). It turns out that
(see [74, Proposition 5.5]). It turns out that  wavelets are needed to generate the space W 0. To motivate this, for a start, let f ∈ V 1 be an arbitrary function. Denote
wavelets are needed to generate the space W 0. To motivate this, for a start, let f ∈ V 1 be an arbitrary function. Denote 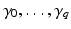 representatives of the q + 1 cosets of
representatives of the q + 1 cosets of 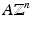 in
in 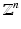 . Then each coset can be written as
. Then each coset can be written as 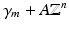 , m = 0,…,q. The function f has the representation
, m = 0,…,q. The function f has the representation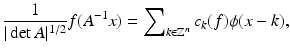
(7)
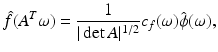
(8)
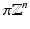 -periodic function c f (ω) with Fourier coefficients
-periodic function c f (ω) with Fourier coefficients 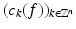 . Then
. Then 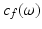 can be decomposed with respect to the cosets:
can be decomposed with respect to the cosets: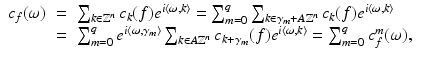
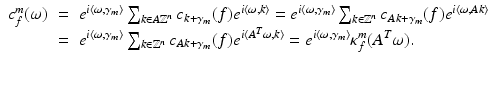
Theorem 6.
Let ϕ ∈ V 0 be a scaling function and let 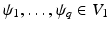 . Then the family
. Then the family 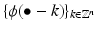 is an orthonormal system if and only if
is an orthonormal system if and only if
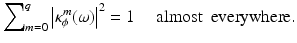
The system 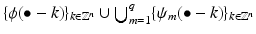 is an orthonormal basis in V 1 if and only if the so-called polyphase matrix
is an orthonormal basis in V 1 if and only if the so-called polyphase matrix
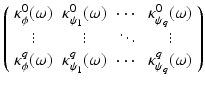 is unitary for almost all
is unitary for almost all  .
.
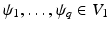 . Then the family
. Then the family 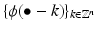 is an orthonormal system if and only if
is an orthonormal system if and only if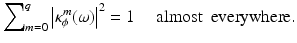
(9)
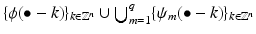 is an orthonormal basis in V 1 if and only if the so-called polyphase matrix
is an orthonormal basis in V 1 if and only if the so-called polyphase matrix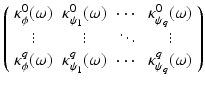
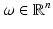 .
.The proof for a more general version of this theorem is given in [74, Sect. 5.2].
A summary and a condition for r-regular wavelets yields in the following theorem.
Theorem 7.
Consider a multiresolution analysis on 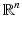 associated with a dilation matrix A.
associated with a dilation matrix A.
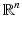 associated with a dilation matrix A.
associated with a dilation matrix A.(i)
Then there exists an associated wavelet set consisting of  functions.
functions.
 functions.
functions. (ii)
If the multiresolution analysis is r-regular and in addition 2q + 1 > n, then there exists an associated wavelet set consisting of q functions, which all are r-regular.
The idea of the proof is that for an r-regular function ϕ on




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree