Digital Imaging
Objectives
At the completion of this chapter, the student should be able to do the following:
• Discuss the difference between binary and decimal number systems.
• Convert binary numbers to decimal and decimal numbers to binary.
• Distinguish between bits, bytes, and words.
• Discuss the requirements on signal sampling to avoid the aliasing artifact.
• Identify spatial frequency domain (k-space).
• Describe spatial localization in a magnetic resonance (MR) image.
Key Terms
When it is applied to medical imaging, the term digital imaging implies that a digital computer is used and that the image is composed of discrete picture elements, that is, pixels.
Magnetic resonance imaging (MRI) could not be performed without the digital computer because the magnetic resonance (MR) signal does not interact directly with a viewable medium as x-rays do with a radiographic intensifying screen phosphor. The MR signal does not present information in a form that can be directly viewed electronically, as does ultrasound.
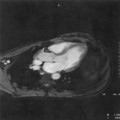
The MR signal provides information about the spatial frequency content of the image rather than directly about the spatial positioning of information in the image. Figure 12-1, A, is a computer-generated image of two bright balls on a dark background. Figure 12-1, B, is a set of projections called a sinogram from that image of the two balls. This type of data set is obtained from a parallel beam x-ray computed tomography (CT) image. The positions and the objects may be inferred at least to a limited extent from the projection data because the data are in the spatial domain, which means that the data are related directly to coordinates in space.
The magnitude of the spatial frequency of the image is shown in Figure 12-1, C. Figure 12-1, D, shows the phase data from the representation of the two balls. Because the MRI data are in the spatial frequency domain, making sense of the raw data from such an MR image is much more difficult than understanding that from a projection radiograph or a CT sinogram.
The MR image is acquired in the spatial frequency domain (k-space).
The digital computer converts this information about the spatial frequency domain into the spatial domain of the MR signal within the patient to produce the image. In this chapter, some characteristics of the digital computer are reviewed and the details of the formation of MR images are examined to explain why MRI is inherently digital.
The Computer’s View of the World
The digital computer works with numbers, specifically, binary numbers. The binary number set consists of 0 and 1. Perhaps if humans had only 2 fingers instead of 10, the binary number system would seem to be more natural than the decimal number system.
A single number in the decimal system is called a digit, as are the fingers shown in Figure 12-2. A single number in the binary system is called a bit, which is short for binary digit.
The digital computer uses the binary number system because it is so easy to implement with real-world components. A 1 is simply defined to be any voltage above a specified value and 0 to be any voltage below a specified value.
Binary Number System
In the binary number system, counting is done by counting 0 and 1 and then over again (Table 12-1). There are only two binary digits, 0 and 1, and the computer performs all operations by converting alphabetic characters, decimal values, and logical functions to binary values.
TABLE 12-1
Organization of Binary Number System
| Decimal Number | Binary Equivalent | Binary Number |
| 0 | 0 | 0 |
| 1 | 20 | 1 |
| 2 | 21 + 0 | 10 |
| 3 | 21 + 20 | 11 |
| 4 | 22 + 0 + 0 | 100 |
| 5 | 22 + 0 + 20 | 101 |
| 6 | 22 + 21 + 0 | 110 |
| 7 | 22 + 21 + 20 | 111 |
| 8 | 23 + 0 + 0 + 0 | 1000 |
| 9 | 23 + 0 + 0 + 20 | 1001 |
| 10 | 23 + 0 + 21 + 0 | 1010 |
| 11 | 23 + 0 + 21 + 20 | 1011 |
| 12 | 23 + 22 + 0 + 0 | 1100 |
| 13 | 23 + 22 + 0 + 20 | 1101 |
| 14 | 23 + 22 + 21 + 0 | 1110 |
| 15 | 23 + 22 + 21 + 20 | 1111 |
| 16 | 24 + 0 + 0 + 0 + 0 | 10000 |
In the binary system, 0 is 0 and 1 is 1. The 1 is actually 20. Any number raised to the zero power is 1; therefore 20 equals 1. In binary notation, the number 2 equals 1 times 21 plus no 20. This is expressed as 10.
The decimal 3 equals 1 times 21 plus 1 times 20 or 11 in binary form. The decimal 4 is 1 times 22 plus no 21 plus no 20 or 100 in binary form. As shown in Table 12-1, each time 2 is raised to an additional power to express a number, the number of binary digits increases by 1.
Easily recognizing the powers of 2 is essential. Power-of-2 notation is used in radiologic imaging to describe image size, image dynamic range (shades of gray), and image storage capacity. Table 12-2 reviews these power notations. In both power notations, the number of zeros to the right of 1 equals the value of the exponent.
TABLE 12-2
Power of 10, Power of 2, and Binary Notation
| Power of 10 | Power of 2 | Binary Notation |
| 100 = 1 | 20 = 1 | 1 |
| 101 = 10 | 21 = 2 | 10 |
| 102 = 100 | 22 = 4 | 100 |
| 103 = 1000 | 23 = 8 | 1000 |
| 104 = 10,000 | 24 = 16 | 10000 |
| 105 = 100,000 | 25 = 32 | 100000 |
| 106 = 1,000,000 | 26 = 64 | 1000000 |
| 27 = 128 | 10000000 | |
| 28 = 256 | 100000000 | |
| 29 = 512 | 1000000000 | |
| 210 = 1024 | 10000000000 |
Digital medical images are made of discrete numerical values arranged in a matrix. The size of the image is described in the binary system of numbers by power-of-2 equivalents. The most popular MR image matrix sizes are 256 × 256 (28 × 28) and 512 × 512 (29 × 29).
Bits, Bytes, and Words
The computer will use as many bits (zeros and ones) as necessary to express a decimal number. The 26 uppercase and 26 lowercase characters of the alphabet and other special characters are usually encoded by 7 bits. The use of 8 bits by newer extended character sets doubles the possible number of characters. Depending on the computer, a string of 8, 16, 32, 64, or possibly some other number of bits is manipulated simultaneously.
To encode is to translate from ordinary characters to computer-compatible characters (binary codes).
Bits are grouped into bunches of 8 called bytes (B). Computer capacity is expressed by the number of bytes the memory of the computer can accommodate. For example, 1 kilobyte (kB) is 210 or 1024 bytes; 1 megabyte (MB) is 220 or 1,048,576 bytes.
Prefixes such as kilo, mega, and giga are not metric in computer use but refer to the nearest power of 2. Popular personal computers have 32-bit or 64-bit microprocessors and contain 2 to 4 GB of main memory. The workstations and minicomputers used in radiology also have main memory capacities of gigabytes, and these values are continuously increasing. Secondary memory in the form of magnetic and optical disks can have memory measured in terabytes (TB) (1 TB = 240 = 1,099,511,627,776 bytes).
Question: How many bits can be stored on a 4 MB chip with a byte size of 8 bits?
Answer: 1,048,576 bytes/MB × 8 bits/byte × 4 MB
220 bytes/MB × 23 bits/byte × 22 MB
Depending on the computer configuration, 1, 2, or 4 bytes usually constitute a word. In the case of a 16-bit microprocessor, a word is 16 consecutive bits of information that are interpreted and shuffled about the computer as a unit. Each word of data in memory has its own address. Often each byte is addressable.
The number of bits determines the resolution or precision of the numbers that the computer manipulates. This means that the number of bits determines the total number of elements that the computer can count.
This is similar to the U.S. Postal Service Zip Codes. When the Postal Service wanted to add resolution to the Zip Codes, it added four more numbers at the end of the five-numeral Zip Code to define the carrier route and the postal zone to which a letter is addressed.
An 8-bit computer number can count from 0 through 255 and thus can represent 256 (28) different values. A 16-bit number can count from 0 through 65,535 and thus can represent 65,536 (216) different values.
Regardless of the number of bits the computer uses, it is limited in the number of distinct values that it can represent. It cannot hold continuous data the way a tape recording, a photograph, or a radiograph can. In the digital computer, limited resolution and limited storage affect the manipulation of data. MRI is limited in the same way.
Quantization or Resolution
Precision.
The limited number of elements the computer can count restricts the precision with which the computer can store values. For proper interpretation, some quantities must be specified with great precision. However, imprecision is a fact of life, and people live comfortably with acceptable degrees of imprecision.
When someone asks, “How far is it to Dallas?” a satisfactory answer is to the nearest mile or so. An answer to the nearest foot or inch is unnecessary. When a person gets a driver’s license, the person’s height is required to the nearest inch, not the nearest quarter inch. Age is not given precisely to the minute but usually only to the year. Such limits of precision are totally satisfactory in everyday life. Considerably more precision is required for MRI.
In the design of a computer system, the required resolution of the data is determined first. For example, differences of 0.01 V may be distinguished in an MR signal—be it a free induction decay (FID), a spin echo (SE), or a gradient echo (GRE). An 8-bit computer word allows for 256 discrete steps or a voltage range from 0 to 2.55 V. A 16-bit computer word gives a voltage range from 0 to 655.35 V.
A voltage range of 24 V is typically used in MRI. Thus, 12 bits (212 = 4096) are required because 12 bits allow a range from 0 to 41.96 V; 11 bits (211 = 2048) provide a range of only 0 to 20.48 V, which would not be sufficient.
A total of 16 or 24 bits are commonly used to allow extra bits for computations. For example, a 22 V signal and 23 V signal are added; 12 bits would not be enough to hold the result, 45 V. An additional bit is required. Although more than ample, computers with word lengths of 32 and 64 bits are becoming more popular as the prices of the computers decrease because they typically offer other attractive features such as faster computation.
Dynamic Range.
One area in which the resolution of the data affects medical images is in the number of gray levels used to display an image. This is referred to as the dynamic range or gray scale resolution of an imaging system. An imaging system that displays only black or white has a gray scale resolution of 21 (1 bit) or 2. Such an image is of very high contrast but displays little information. Although the value of each pixel is unimportant, the number of values is extremely important in determining the final image.
The range of pixel values in an image is the dynamic range or gray scale resolution.
In MR images, gray scale resolution refers to how small a difference in pixel intensity corresponds to a 1-bit difference in pixel value. Visually, gray scale resolution refers to the number of different shades of gray that can be perceived.
The gray scale resolution of the human eye is somewhere between 24 (4 bits) and 25 (5 bits) or 16 to 32, shades of gray, stretching from black to white. The gray scale resolution of the MR signal from the patient exceeds 210 (10 bits).
Related posts:
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
