([1])
The mean squared displacement can then be calculated from the second moment of this distribution:
![$$ < {r^2}(t) \ge \left(\int\int {\int}\right)_{{-\infty}}^{\infty}{{{\left[\left({x^2} + {y^2} + {z^2}\right)\right]p\left(r,t\right)\textrm{d}x\textrm{d}y\textrm{d}z} = 6Dt}}$$](/wp-content/uploads/2017/02/A184233_1_En_7_Chapter_Equ2.gif)
![$$ < {r^2}(t) \ge \left(\int\int {\int}\right)_{{-\infty}}^{\infty}{{{\left[\left({x^2} + {y^2} + {z^2}\right)\right]p\left(r,t\right)\textrm{d}x\textrm{d}y\textrm{d}z} = 6Dt}}$$](/wp-content/uploads/2017/02/A184233_1_En_7_Chapter_Equ2.gif)
([2])
This is the well-known Einstein equation of diffusion and this model is used to derive the NMR signal attenuation due to diffusion of molecules (4, 7).
Most modern diffusion imaging techniques employ variations of bipolar pulsed field gradient methods (8) to obtain diffusion sensitivity. In these sequences, two magnetic field gradients are applied sequentially to dephase and then rephase spins or protons. Any spins that have moved in the interval between the two gradients do not experience similar magnetic field as during the first gradient and thus they do not get rephased, resulting in a net loss of spin coherence and a quantifiable loss in the MRI signal (9) which can be related to the apparent diffusion coefficient or ADC. In the simplest case, with spin-echo MRI and considering for the moment only a single diffusion coefficient per voxel, it can be shown (starting from the Einstein formulation of diffusion) that the signal and the ADC are related as follows (10):
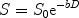
where S is the measured signal, S 0 the signal in absence of the gradients, and D is the ADC. The b-factor in this equation is a function of the gradient strength G, duration δ, and time separation Δ between the gradient pulses. The b-factor must be calculated for each sequence, which can be non-trivial when the diffusion gradients interact with the imaging gradients in a complicated fashion. For the simple case where imaging gradients and the resultant cross terms in the b-factor calculations are ignored, 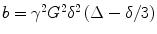 , (10) where γ is a physical constant, the gyromagnetic ratio. D can be determined from the above equation if at least two images are acquired with different diffusion weightings (and thus different b-factors). It also becomes evident from this equation that any movement of spins during the diffusion time Δ will result in MRI signal loss. Thus diffusion MRI is sensitive to all motion of molecules during the sequence, and not just purely diffusive motion. Moreover, the observed diffusion coefficients in tissues reflect diffusion in several compartments—extracellular and intracellular, intranuclear, mitochondrial, etc. —which may all have different diffusivities if one could resolve them. It is for these reasons that the diffusion coefficient and tensor as measured with MRI are called the apparent diffusion coefficient (ADC) and apparent diffusion tensor (ADT), respectively.
, (10) where γ is a physical constant, the gyromagnetic ratio. D can be determined from the above equation if at least two images are acquired with different diffusion weightings (and thus different b-factors). It also becomes evident from this equation that any movement of spins during the diffusion time Δ will result in MRI signal loss. Thus diffusion MRI is sensitive to all motion of molecules during the sequence, and not just purely diffusive motion. Moreover, the observed diffusion coefficients in tissues reflect diffusion in several compartments—extracellular and intracellular, intranuclear, mitochondrial, etc. —which may all have different diffusivities if one could resolve them. It is for these reasons that the diffusion coefficient and tensor as measured with MRI are called the apparent diffusion coefficient (ADC) and apparent diffusion tensor (ADT), respectively.
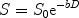
([3])
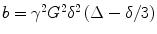 , (10) where γ is a physical constant, the gyromagnetic ratio. D can be determined from the above equation if at least two images are acquired with different diffusion weightings (and thus different b-factors). It also becomes evident from this equation that any movement of spins during the diffusion time Δ will result in MRI signal loss. Thus diffusion MRI is sensitive to all motion of molecules during the sequence, and not just purely diffusive motion. Moreover, the observed diffusion coefficients in tissues reflect diffusion in several compartments—extracellular and intracellular, intranuclear, mitochondrial, etc. —which may all have different diffusivities if one could resolve them. It is for these reasons that the diffusion coefficient and tensor as measured with MRI are called the apparent diffusion coefficient (ADC) and apparent diffusion tensor (ADT), respectively.
, (10) where γ is a physical constant, the gyromagnetic ratio. D can be determined from the above equation if at least two images are acquired with different diffusion weightings (and thus different b-factors). It also becomes evident from this equation that any movement of spins during the diffusion time Δ will result in MRI signal loss. Thus diffusion MRI is sensitive to all motion of molecules during the sequence, and not just purely diffusive motion. Moreover, the observed diffusion coefficients in tissues reflect diffusion in several compartments—extracellular and intracellular, intranuclear, mitochondrial, etc. —which may all have different diffusivities if one could resolve them. It is for these reasons that the diffusion coefficient and tensor as measured with MRI are called the apparent diffusion coefficient (ADC) and apparent diffusion tensor (ADT), respectively.The diffusivity of a substance is not always identical in all directions. For example, diffusion coefficients can be relatively large in one direction and small in another. Diffusion is more generally characterized by a second-order tensor, or a matrix of nine coefficients:
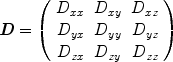
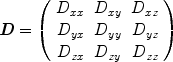
([4])
This implies that nine diffusivities would have to be determined to measure the tensor. However, the diffusion tensor is symmetric, meaning that 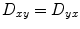 ,
, 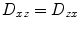 , and
, and 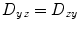 . Thus, only six diffusivities need to be determined. When the axes of the measurement system coincide exactly with the axes of the fiber or object being studied, the off-diagonal elements of the tensor (i.e., D xy , D xz , and D yz ) become zero, and the measured diagonal diffusivites D xx , D yy , and D zz are termed the principal diffusivities, often annotated D 11, D 22, and D 33 or λ 1, λ 2 , and λ 3. Of course, in the general case, the measurement and principal axes of diffusion do not coincide for most fibers. In such a case, these principal diffusivities, which are also called the eigenvalues of the diffusion tensor, along with the eigenvectors of the system (defining the directions of the principal diffusivities), can be calculated from the measured tensor by a simple mathematical transformation (see Note 1).
. Thus, only six diffusivities need to be determined. When the axes of the measurement system coincide exactly with the axes of the fiber or object being studied, the off-diagonal elements of the tensor (i.e., D xy , D xz , and D yz ) become zero, and the measured diagonal diffusivites D xx , D yy , and D zz are termed the principal diffusivities, often annotated D 11, D 22, and D 33 or λ 1, λ 2 , and λ 3. Of course, in the general case, the measurement and principal axes of diffusion do not coincide for most fibers. In such a case, these principal diffusivities, which are also called the eigenvalues of the diffusion tensor, along with the eigenvectors of the system (defining the directions of the principal diffusivities), can be calculated from the measured tensor by a simple mathematical transformation (see Note 1).
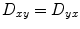 ,
, 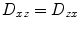 , and
, and 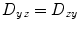 . Thus, only six diffusivities need to be determined. When the axes of the measurement system coincide exactly with the axes of the fiber or object being studied, the off-diagonal elements of the tensor (i.e., D xy , D xz , and D yz ) become zero, and the measured diagonal diffusivites D xx , D yy , and D zz are termed the principal diffusivities, often annotated D 11, D 22, and D 33 or λ 1, λ 2 , and λ 3. Of course, in the general case, the measurement and principal axes of diffusion do not coincide for most fibers. In such a case, these principal diffusivities, which are also called the eigenvalues of the diffusion tensor, along with the eigenvectors of the system (defining the directions of the principal diffusivities), can be calculated from the measured tensor by a simple mathematical transformation (see Note 1).
. Thus, only six diffusivities need to be determined. When the axes of the measurement system coincide exactly with the axes of the fiber or object being studied, the off-diagonal elements of the tensor (i.e., D xy , D xz , and D yz ) become zero, and the measured diagonal diffusivites D xx , D yy , and D zz are termed the principal diffusivities, often annotated D 11, D 22, and D 33 or λ 1, λ 2 , and λ 3. Of course, in the general case, the measurement and principal axes of diffusion do not coincide for most fibers. In such a case, these principal diffusivities, which are also called the eigenvalues of the diffusion tensor, along with the eigenvectors of the system (defining the directions of the principal diffusivities), can be calculated from the measured tensor by a simple mathematical transformation (see Note 1).In an environment where the barriers to diffusion are identical in all directions, diffusion is considered isotropic. This is the case, for example, in a cup of water, where even if molecules are allowed to diffuse for relatively long times, they are unlikely to encounter a barrier to diffusion so that movement in one direction is not favored over any other. In such situations, the diffusion coefficients in all directions are equivalent (i.e., 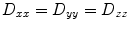 , etc.). For isotropic cases, measurement of a single scalar coefficient suffices to completely characterize the system. This condition is often not met in tissue measurements where cell membranes, packing, and other ordering in tissue structures promote directed water diffusion. For medical imaging applications, this is the case for example in white matter, muscle, cartilage, kidneys, tumors, and in the lens of the eye (11–19). In such settings, diffusion is said to be anisotropic, reflecting the non-equal diffusivities in various directions.
, etc.). For isotropic cases, measurement of a single scalar coefficient suffices to completely characterize the system. This condition is often not met in tissue measurements where cell membranes, packing, and other ordering in tissue structures promote directed water diffusion. For medical imaging applications, this is the case for example in white matter, muscle, cartilage, kidneys, tumors, and in the lens of the eye (11–19). In such settings, diffusion is said to be anisotropic, reflecting the non-equal diffusivities in various directions.
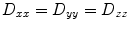 , etc.). For isotropic cases, measurement of a single scalar coefficient suffices to completely characterize the system. This condition is often not met in tissue measurements where cell membranes, packing, and other ordering in tissue structures promote directed water diffusion. For medical imaging applications, this is the case for example in white matter, muscle, cartilage, kidneys, tumors, and in the lens of the eye (11–19). In such settings, diffusion is said to be anisotropic, reflecting the non-equal diffusivities in various directions.
, etc.). For isotropic cases, measurement of a single scalar coefficient suffices to completely characterize the system. This condition is often not met in tissue measurements where cell membranes, packing, and other ordering in tissue structures promote directed water diffusion. For medical imaging applications, this is the case for example in white matter, muscle, cartilage, kidneys, tumors, and in the lens of the eye (11–19). In such settings, diffusion is said to be anisotropic, reflecting the non-equal diffusivities in various directions.The coefficients along the x, y, and z-directions (D xx , D yy , and D zz ) are simply the diagonal terms of the tensor and are the principal diffusivities of the system only when the laboratory coordinate frame coincides with that of the sample orientation. In the general case where the laboratory axes are different from the orientation of the sample, the principal diffusivities are found by determining the eigenvalues of the measured diffusion matrix (1, 15, 16). These principal diffusivities are independent of the relation between the coordinate system of the laboratory and the coordinate system of the sample (1, 16).
The tensor nature of diffusion must be taken into account in the mathematical framework for describing diffusion. Torrey derived the Bloch equations with diffusion terms and included the rudiments of the tensor analysis needed to consider anisotropic diffusion (20). In 1965, Stejskal extended this analysis to give a formal description of the effect of anisotropic diffusion on the NMR signal (7). Basser et al. further extended this treatment and measured the ADT by applying gradients in various directions (15, 16). Starting with the mathematical expressions for the description of magnetization in the presence of spin diffusion (20) they derived the expressions necessary to calculate the various terms of D (or ADT) from an MRI experiment. They showed that
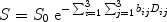
where
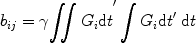
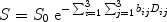
([5])
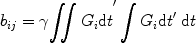
([6])
Here, the indices i and j represent the measurement axes (1, 2, and 3 being x, y, and z, respectively). G i and G j thus represent the applied diffusion gradients in various directions. This equation bears obvious resemblance to the case for measuring a single diffusion coefficient. However, all six unique diffusivities must be accounted for, and thus this implies that at least seven images must be acquired to completely determine the seven variables in this equation (S 0 and the six unique diffusivities). Obviously, the calculation of the b-matrix as per Eq. [6] is considerably more complex than that of b-factors for a uni-directional experiment and care must be taken to account for the interaction between the various diffusion and imaging gradients.
2 Materials
2.1 In Vivo Imaging
The following MR-system-compatible materials are essential for running a DTI experiment in small rodents. The procedure for setting up the experiment on excised tissue (excision, fixation, insertion, etc.) is not described, but the mechanics of the DTI experiment would be similar other than the obviation of the need for anesthesia equipment.
1.
A small-bore high field strength whole body animal MRI scanner—typically, scanners between 4.7 T and 17.5 T and having maximum gradient capabilities between 400 and 1000 mT/m are used for rodent diffusion tensor imaging.
2.
Calibrated small rodent inhalation anesthesia equipment such as (E-Z Anesthesia, Euthanex Corporation, Palmer, PA) located outside the MR room, is used for both induction and maintenance of anesthesia.
3.
A small animal monitoring and gating system (Model 1025 by SA Instruments, Inc., Stony Brook, NY) consisting of a fan that drives a set percentage of heat to the animal in the scanner is typically employed. This continuously monitors several of the animal’s physiological parameters such as respiration, body temperature, heart rate, and ECG during the experiment. The system should be equipped with a gating module which can be set to selectively acquire data during a desired phase of respiration if needed.
4.
A rat or mouse bed furnished with nonmagnetic ear and tooth bars (Bruker Biospin MRI, Inc., Billerica, MA).
5.
A rectal temperature probe (SA Instruments, Inc., Stony Brook, NY).
6.
A respiration pillow sensor pad (SA Instruments, Inc., Stony Brook, NY).
7.
Masking tape (Scotch 234) used to tape down the respiration pad on to the chest of the animal and to restrict excessive motion from other regions of the animal.
8.
A heating module fan serving as a direct source of heat to the animal (SA Instruments, Inc., Stony Brook, NY).
9.
Acquisition and data processing software, e.g., MATLAB (The Mathworks, Natick, MA) or ParaVision 4.0 software implemented on the MRI scanner.
2.2 Transcardial Perfusion for Ex Vivo Sample Preparation
1.
Ringer’s solution: Prepare 7.2 g NaCL, 0.17 g CaCl2, 0.37 g KCl and dissolve in reagent-grade H2O, and bring the final volume to 1 L. Adjust the pH to 7.3–7.4. Once thoroughly dissolved, filter through a 0.22-μm filter, aliquot into single-use volumes (25–50 mL), and autoclave.
2.
BD 30 G 1 inch PrecisionGlide needle from Fisher Scientific.
3.
Surgical instruments for transcardial perfusion such as thumb forceps, 120 mm; tissue forceps, 115 mm; and eye scissors, 115 mm (Harvard Apparatus).
4.
Mini-pump variable flow (Fisher Scientific).
5.
Phosphate-buffered saline (PBS): Prepare 0.13 M NaCl (Sigma), 0.0027 M KCl (Sigma), 0.01 M Na2HPO4 (Sigma), 0.0018 M KH2PO4 (Sigma) in 1 L dd H2O. Adjust pH to 7.4 with HCl and NaOH. Autoclave before storage at room temperature.
6.
Four percent paraformaldehyde (Sigma): Prepare a 4% (w/v) solution in PBS. The solution has to be carefully heated and not allowed to boil using a stirring hot plate in a fume hood) to dissolve. The solution is filtered and then cooled to room temperature for use.
3 Methods
3.1 Pre-scan Check
1.
MRI scanners are large, powerful magnets and their magnetic strength should never be underestimated. Any and all loose metals from both the operator and the animal (such as ear tags) must be removed prior to entry into the scanner room, with or without the animal.
2.
Apart from strict daily quality checks for proper running and maintenance of the scanner hardware, steps should be taken to check the system for smooth running of experiments (see Note 2).
3.
It is important to ensure that there is enough anesthetic (i.e., isoflurane) for the duration of the experiment and that all physiological monitors are working properly before an animal is anesthetized.
4.
The animal should be positioned in either rat or mouse coil and at the specified distance from the isocenter of the magnet. A phantom can be used in addition to boost signal-to-noise ratio. Improper measurement or calculation (see Note 3) will result in inability to acquire ideal data and is unnecessary waste of time. This is because the animal has to be pulled out during the course of the experiment and the repositioning process restarted.
3.2 Animals
1.
An animal’s identification is correctly entered into the software and desired protocol selected before the start of experiment.
2.
Inhalation anesthetic is generally preferred to an injectible one because it allows for safer, faster induction and quick recovery. The animal is placed in an induction chamber and anesthesia is rapidly induced using 3% isoflurane in oxygen at a flow rate of 2 L/min (typical). It is very important to watch the animal very closely at this time because of varied strain and individual differences in response to anesthesia. It should be ensured that the animal reaches the desired depth of anesthesia, which can be tested by the pedal withdrawal reflex. A slight pressure is placed on the animal’s hind limb and if this causes the foot to be withdrawn, the animal is lightly anesthetized. However, this reflex is absent in deeply anesthetized animals.
3.
After induction, the animal is immediately placed in either the prone or the supine position on a bed connected to another oxygen and isoflurane inlet and anesthesia is maintained at 1 to 1.5% at the same flow rate as at induction.
4.




A rectal thermometer is inserted and its temperature should be registered on the monitor. The body temperature is maintained at 37°C or at the initial starting temperature. At this point, the source of heat should be directed toward the animal (but not too close) and temperature carefully and constantly monitored and controlled to avoid induction of hypothermia or hyperthermia which affects the outcome of MRI data.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree