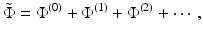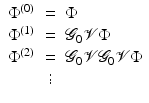Fig. 1
Optical transillumination measurements made with a time-resolved system (left) or an intensity-modulated system (right)
Spectroscopic Measurements
Attenuation of light in the near infrared (NIR) is due to absorption and scattering. The parameter of most interest is absorption which is caused by chromophores of variable concentration such as hemoglobin in its oxygenated and deoxygenated states. In the absence of scattering, the change in light intensity obeys the Beer–Lambert law
![$$\displaystyle{ -\ln \frac{I_{{\mathrm{in}}}} {I_{{\mathrm{out}}}} =\mu _{{\mathrm{a}}}\,d =\alpha _{c}[c]d, }$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_Equ1.gif)
where d is the source-detector separation, which is equal to the optical path length, [c] is the concentration of chromophore c, and α c is the absorption coefficient per unit length per unit concentration of chromophore c and can usually be obtained in vitro. In the presence of scattering, the optical path length of transmitted photons follows a much more complex relationship. Hence, attenuation measurements alone do not allow quantification of chromophore concentration.
![$$\displaystyle{ -\ln \frac{I_{{\mathrm{in}}}} {I_{{\mathrm{out}}}} =\mu _{{\mathrm{a}}}\,d =\alpha _{c}[c]d, }$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_Equ1.gif)
(1)
Continuous intensity (DC) instruments measure changes in the intensity of light leaving the tissue surface [56]. This is frequently done in a purely spectroscopic manner, i.e., to obtain only global changes in chromophore concentration. In order to quantify concentration changes, additional information is required. One approach is to derive an approximate differential path length factor (DPF) , which restores the approximate Beer–Lambert law for small changes in concentration
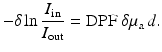
Since there are typically several contributing chromophores, light of different wavelengths in the NIR region is employed, and regression techniques are used to find their relative weightings [26]. It was shown empirically [29] that the DPF is simply the mean time of light multiplied by the speed of light in the tissue. In fact, this relationship follows naturally from the diffusion approximation of light transport [8]. Furthermore, it is equally well approximated by the change in phase of an intensity-modulated system, at least at low modulation frequencies.
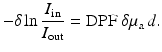
(2)
Intensity-modulated measurements were first reported by [69]. Most systems use a heterodyne technique to mix the transmitted light with a reference beam of slightly different modulation frequency, thus producing a lower frequency envelope that is easier to detect using RF equipment. Time-resolved systems were first developed using a streak camera [29, 49, 73], an instrument with exceptionally high time resolution in the picosecond range but with high cost, relatively low dynamic range, and a significant inherent temporal nonlinearity due to a sinusoidal ramp voltage. Alternatively, time-correlation single photon counting (TCSPC) systems measure arrival times of individual photons by comparison with a reference pulse using a time-to-amplitude converter (TAC) device [20, 79, 83]. These systems have a high dynamic range and excellent temporal linearity.
Imaging Systems
Imaging methods can be divided into direct systems which seek to detect heterogeneities in tissue by analyzing the transmitted (or, in some cases, reflected) light and indirect systems which attempt to solve the inverse problem of image reconstruction. The latter is the main emphasis of this article although the former is historically the precedent, in a similar manner in which x-ray radiographs were the precursor to x-ray computed tomography (CT).
Transillumination of candle light for a patient suffering from hydrocephalus was reported as early as 1831, but the first significant attempt at diagnostic imaging using optical radiation was for breast lesions and was made by Cutler [27], who used a lamp held under the breast in a darkened room. However, even at this stage, multiple scattering effects caused a notable degradation in image quality. The recognition of this fact led to many attempts to eliminate or minimize the degradation due to scattering ranging from collimation [55] and polarization discrimination [84] to coherence gating using holographic gating [90] or heterodyne detection [82].
With the introduction of time-resolved detectors came the natural attempt to use temporal gating to discriminate early arriving photons (which necessarily have the shortest optical path and therefore suffer the least number of scatterings) from later arriving photons which have undergone multiple scatterings and therefore have ill-determined photon paths. The early implementations of this idea used a Kerr gate as an ultrafast shutter [99]. However, this technique is limited to relatively low-scattering media due to the small dynamic range of the Kerr shutter. Other studies have been based on the streak camera [42] or TCSPC [19] systems described in section “Spectroscopic Measurements.”
The attempt to physically discriminate between photons that have undergone different numbers of scattering events is inherently limited by the statistical likelihood of the low scattering number photons arriving at the detector. For the relatively optically thick tissues that are of interest in breast cancer screening or brain imaging, these photons are overwhelmed by noise. For this reason, indirect methods that solve an inverse problem based on recovering the spatially varying optical parameters that provide the best fit of a photon transport model with the measured data are becoming more prevalent. Within this framework, the three basic strategies (time resolved, intensity modulated, and DC systems) have all been developed and reported. In addition, many different geometrical arrangements have been investigated. Initial studies have been on 2D slice-by-slice imaging, although it is apparent that the photon propagation must in reality be described by a 3D model. Fully 3D methods are now appearing.
In the remainder of this article, we will discuss the inverse problem and the strategies that have been adopted in order to solve it. In order to analyze this problem, we first have to consider the model of photon transport in dense media.
3 Mathematical Modeling and Analysis
Radiative Transfer Equation
In optical imaging, light transport through a medium containing scattering particles is described by transport theory [54]. In transport theory , the particle conservation within a small volume element of phase space is investigated. The wave phenomenon of particles is ignored. The transport theory can be modeled through stochastic methods and deterministic methods. In the stochastic approach, individual particle interactions are modeled as the particles are scattered and absorbed within the medium. The two stochastic methods that have been used in optical imaging are the Monte Carlo method and the random walk theory, of which two, the Monte Carlo is the most often used [5].
In deterministic approach, particle transport is described with integrodifferential equations which can be solved either analytically or numerically [5]. In optical imaging, a widely accepted model for light transport is the radiative transport equation (RTE). The RTE is a one-speed approximation of the transport equation, and thus it basically assumes that the energy (or speed) of the particles does not change in collisions and that the refractive index is constant within the medium. For discussion of photon transport in medium with spatially varying refractive index, see, e.g., [16, 36, 62, 72].
Let 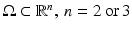 denote the physical domain where n is the dimension of the domain. The medium is considered isotropic in the sense that the probability of scattering between two directions depends only on the relative angle between those directions and not on an absolute direction. For discussion of light propagation in anisotropic medium, see, e.g., [44]. Furthermore, let
denote the physical domain where n is the dimension of the domain. The medium is considered isotropic in the sense that the probability of scattering between two directions depends only on the relative angle between those directions and not on an absolute direction. For discussion of light propagation in anisotropic medium, see, e.g., [44]. Furthermore, let 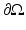 denote the boundary of the domain and
denote the boundary of the domain and 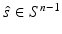 denote a unit vector in the direction of interest. The RTE is written in time domain as
denote a unit vector in the direction of interest. The RTE is written in time domain as
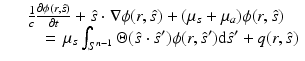
and in frequency domain as
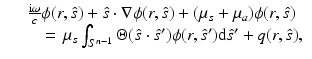
where c is the speed of light in the medium, i is the imaginary unit, ω is the angular modulation frequency of the input signal, and μ s = μ s (r) and μ a = μ a (r) are the scattering and absorption coefficients of the medium, respectively. The scattering coefficient represents the probability per unit length of a photon being scattered, and the absorption coefficient represents the probability per unit length of a photon being absorbed. Furthermore, 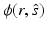 is the radiance,
is the radiance, 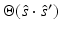 is the scattering phase function, and
is the scattering phase function, and 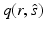 is the source inside
is the source inside 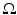 . The radiance can be defined such that the amount of power transfer in the infinitesimal angle
. The radiance can be defined such that the amount of power transfer in the infinitesimal angle 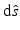 in direction
in direction 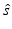 at time t through an infinitesimal area dS is given by
at time t through an infinitesimal area dS is given by
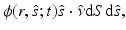 where
where 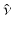 is the normal to the surface dS [54]. The scattering phase function
is the normal to the surface dS [54]. The scattering phase function 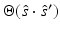 describes the probability that a photon with an initial direction
describes the probability that a photon with an initial direction 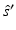 will have a direction
will have a direction 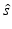 after a scattering event. In optical imaging, the most usual phase function for isotropic material is the Henyey–Greenstein scattering function [47] which is of the form
after a scattering event. In optical imaging, the most usual phase function for isotropic material is the Henyey–Greenstein scattering function [47] which is of the form
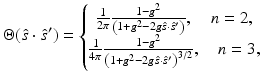
where g is the scattering shape parameter that defines the shape of the probability density and it gets values between − 1 < g < 1. With the value g = 0, the scattering probability density is a uniform distribution. For forward dominated scattering, g > 0, and for backward dominated scattering, g < 0. The time-domain and frequency-domain representations of the RTE are related through Fourier transform.
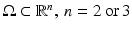 denote the physical domain where n is the dimension of the domain. The medium is considered isotropic in the sense that the probability of scattering between two directions depends only on the relative angle between those directions and not on an absolute direction. For discussion of light propagation in anisotropic medium, see, e.g., [44]. Furthermore, let
denote the physical domain where n is the dimension of the domain. The medium is considered isotropic in the sense that the probability of scattering between two directions depends only on the relative angle between those directions and not on an absolute direction. For discussion of light propagation in anisotropic medium, see, e.g., [44]. Furthermore, let 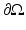 denote the boundary of the domain and
denote the boundary of the domain and 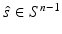 denote a unit vector in the direction of interest. The RTE is written in time domain as
denote a unit vector in the direction of interest. The RTE is written in time domain as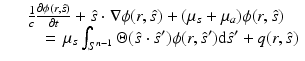
(3)
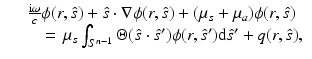
(4)
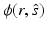 is the radiance,
is the radiance, 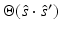 is the scattering phase function, and
is the scattering phase function, and 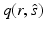 is the source inside
is the source inside  . The radiance can be defined such that the amount of power transfer in the infinitesimal angle
. The radiance can be defined such that the amount of power transfer in the infinitesimal angle 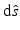 in direction
in direction 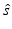 at time t through an infinitesimal area dS is given by
at time t through an infinitesimal area dS is given by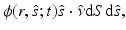
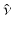 is the normal to the surface dS [54]. The scattering phase function
is the normal to the surface dS [54]. The scattering phase function 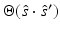 describes the probability that a photon with an initial direction
describes the probability that a photon with an initial direction 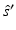 will have a direction
will have a direction 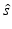 after a scattering event. In optical imaging, the most usual phase function for isotropic material is the Henyey–Greenstein scattering function [47] which is of the form
after a scattering event. In optical imaging, the most usual phase function for isotropic material is the Henyey–Greenstein scattering function [47] which is of the form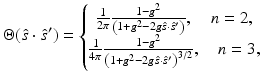
(5)
In order to obtain a unique solution for the RTE, the ingoing radiance distribution on the boundary 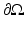 , that is,
, that is, 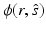 for
for 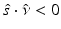 , where
, where 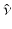 is the outward unit normal, needs to be known [24]. Several boundary conditions can be applied to the RTE [1, 33, 57]. In optical imaging, the boundary condition which assumes that no photons travel in an inward direction at the boundary
is the outward unit normal, needs to be known [24]. Several boundary conditions can be applied to the RTE [1, 33, 57]. In optical imaging, the boundary condition which assumes that no photons travel in an inward direction at the boundary 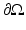 is used [5]
is used [5]
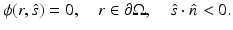
This boundary condition, also known as the free surface boundary condition and the vacuum boundary condition, implies that once a photon escapes the domain  , it does not reenter it. The boundary condition (6) can be modified to include a boundary source
, it does not reenter it. The boundary condition (6) can be modified to include a boundary source  at the source position
at the source position  , and it can be written in the form [96]
, and it can be written in the form [96]
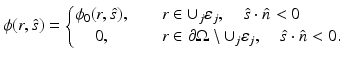
In optical imaging, the measurable quantity is the exitance J n (r) on the boundary of the domain. It is defined as [5]
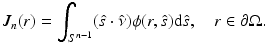
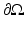 , that is,
, that is, 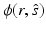 for
for 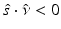 , where
, where 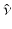 is the outward unit normal, needs to be known [24]. Several boundary conditions can be applied to the RTE [1, 33, 57]. In optical imaging, the boundary condition which assumes that no photons travel in an inward direction at the boundary
is the outward unit normal, needs to be known [24]. Several boundary conditions can be applied to the RTE [1, 33, 57]. In optical imaging, the boundary condition which assumes that no photons travel in an inward direction at the boundary 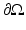 is used [5]
is used [5]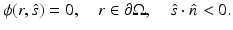
(6)
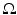 , it does not reenter it. The boundary condition (6) can be modified to include a boundary source
, it does not reenter it. The boundary condition (6) can be modified to include a boundary source 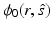 at the source position
at the source position 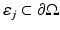 , and it can be written in the form [96]
, and it can be written in the form [96]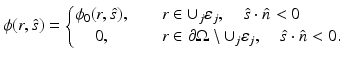
(7)
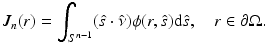
(8)
Diffusion Approximation
In optical imaging, light propagation in tissues is usually modeled with the diffusion approximation (DA) to the RTE. The most typical approach to derive the DA from the RTE is to expand the radiance, the source term, and the phase function into series using the spherical harmonics and truncate the series [5, 24, 33]. If the spherical harmonics series is truncated at the Nth moment, P N approximation is obtained [5, 33]. The first-order spherical harmonics approximation is referred to as the P 1 approximation, and the DA can be regarded as a special case for that. The most typical approach for utilizing the P N approximations in optical imaging has been to use them in angular discretization of the numerical solution of the RTE [14, 100].
An alternative to the P N approximation is the Boltzmann hierarchy approach , in which moments of radiance are used to form a set of coupled equations that approximate the RTE [38]. Furthermore, the DA can be derived using asymptotic techniques [7, 17] leading to generalized diffusion equation or by using projection algebra [33, 57]. If the speed of light is not constant, a diffusion equation with spatially varying indices of refraction can be derived [16].
Here, a short review of the derivation of the DA is given according to [54, 57]. First, the P 1 approximation is derived, and then, the DA is formed as a special case for that. In the DA framework, the radiance is approximated by
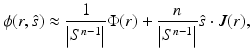
where 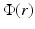 and J(r) are the photon density and photon current which are defined as
and J(r) are the photon density and photon current which are defined as
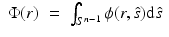
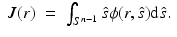
By inserting the approximation (9) and similar approximations written for the source term and phase function into Eq. 4 and following the derivation in [5, 54], the P 1 approximation is obtained
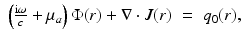
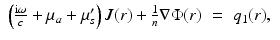
where 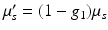 is the reduced scattering coefficient, q 0(r) and q 1(r) are the isotropic and dipole components of the source, and g 1 is the mean of the cosine of the scattering angle [5, 57]
is the reduced scattering coefficient, q 0(r) and q 1(r) are the isotropic and dipole components of the source, and g 1 is the mean of the cosine of the scattering angle [5, 57]
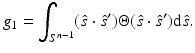
In the case of the Henyey–Greenstein scattering function , Eq. 5, we have g 1 = g.
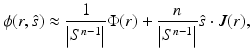
(9)
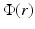 and J(r) are the photon density and photon current which are defined as
and J(r) are the photon density and photon current which are defined as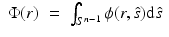
(10)
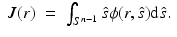
(11)
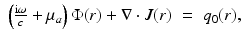
(12)
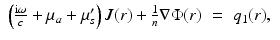
(13)
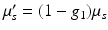 is the reduced scattering coefficient, q 0(r) and q 1(r) are the isotropic and dipole components of the source, and g 1 is the mean of the cosine of the scattering angle [5, 57]
is the reduced scattering coefficient, q 0(r) and q 1(r) are the isotropic and dipole components of the source, and g 1 is the mean of the cosine of the scattering angle [5, 57]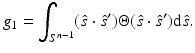
(14)
To derive the diffusion approximation, it is further assumed that the light source is isotropic, thus q 1(r) = 0, and that 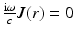 . The latter assumption, which in time-domain case is of the form
. The latter assumption, which in time-domain case is of the form 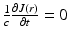 , is usually justified by specifying the condition
, is usually justified by specifying the condition 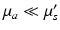 [5]. Utilizing these approximations, Eq. 13 gives the Fick’s law
[5]. Utilizing these approximations, Eq. 13 gives the Fick’s law
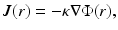
where
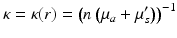
is the diffusion coefficient. Substituting Eq. 15 into Eq. 12, the frequency-domain version of the DA is obtained. It is of the form
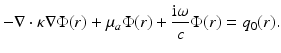
The DA has an analogue in time domain as well. It is of the form
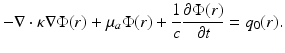
The time-domain and frequency-domain representations of the DA are related through Fourier transform, similarly as in the case of the RTE.
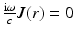 . The latter assumption, which in time-domain case is of the form
. The latter assumption, which in time-domain case is of the form 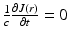 , is usually justified by specifying the condition
, is usually justified by specifying the condition 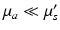 [5]. Utilizing these approximations, Eq. 13 gives the Fick’s law
[5]. Utilizing these approximations, Eq. 13 gives the Fick’s law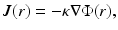
(15)
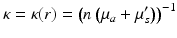
(16)
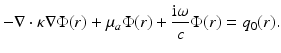
(17)
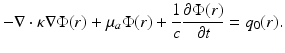
(18)
Boundary Conditions for the DA
The boundary condition (6) cannot be expressed in terms of variables of the diffusion approximation. Instead, there are a few boundary conditions that have been applied to the DA. The simplest boundary condition is the Dirichlet boundary condition which is also referred to as the zero-boundary condition . It sets the photon density to zero on the boundary; thus, 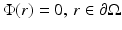 [40, 87]. Alternatively, an extrapolated boundary condition can be used [33, 40, 87]. In the approach, the photon density is set to zero on an extrapolated boundary which is a virtual boundary outside the medium located at a certain distance from the real boundary. Both the zero-boundary condition and the extrapolated boundary condition are physically incorrect, and they have mostly been used because of their mathematical simplicity [40].
[40, 87]. Alternatively, an extrapolated boundary condition can be used [33, 40, 87]. In the approach, the photon density is set to zero on an extrapolated boundary which is a virtual boundary outside the medium located at a certain distance from the real boundary. Both the zero-boundary condition and the extrapolated boundary condition are physically incorrect, and they have mostly been used because of their mathematical simplicity [40].
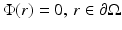 [40, 87]. Alternatively, an extrapolated boundary condition can be used [33, 40, 87]. In the approach, the photon density is set to zero on an extrapolated boundary which is a virtual boundary outside the medium located at a certain distance from the real boundary. Both the zero-boundary condition and the extrapolated boundary condition are physically incorrect, and they have mostly been used because of their mathematical simplicity [40].
[40, 87]. Alternatively, an extrapolated boundary condition can be used [33, 40, 87]. In the approach, the photon density is set to zero on an extrapolated boundary which is a virtual boundary outside the medium located at a certain distance from the real boundary. Both the zero-boundary condition and the extrapolated boundary condition are physically incorrect, and they have mostly been used because of their mathematical simplicity [40].The most often used boundary condition in optical imaging is the Robin boundary condition which is also referred to as the partial current boundary condition [4, 24, 33, 40, 54, 87]. It can be derived as follows. Within the P 1 approximation framework (9), the total inward- and outward-directed photon fluxes at a point 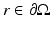 are
are
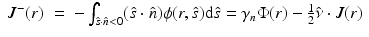
![$$\displaystyle\begin{array}{rcl} J^{+}(r)& =& \int _{\hat{ s}\cdot \hat{n}>0}(\hat{s} \cdot \hat{n})\phi (r,\hat{s}){\mathrm{d}}\hat{s} =\gamma _{n}\Phi (r) + \frac{1} {2}\hat{\nu } \cdot J(r),{}\end{array}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_Equ20.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(20)</DIV></DIV>where <SPAN class=EmphasisTypeItalic>γ</SPAN> <SUB><SPAN class=EmphasisTypeItalic>n</SPAN> </SUB>is a dimension-dependent constant which obtains values <SPAN class=EmphasisTypeItalic>γ</SPAN> <SUB>2</SUB> = 1∕<SPAN class=EmphasisTypeItalic>π</SPAN> and <SPAN class=EmphasisTypeItalic>γ</SPAN> <SUB>3</SUB> = 1∕4 [<CITE><A href=]() 57]. To derive the Robin boundary condition for the DA, it is assumed that the total inward-directed photon flux on the boundary is zero; thus,
57]. To derive the Robin boundary condition for the DA, it is assumed that the total inward-directed photon flux on the boundary is zero; thus,
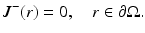
Utilizing Eq. 19 and the Fick’s law (15), the Robin boundary condition can be derived. It is of the form
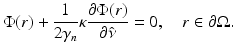
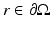 are
are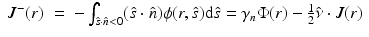
(19)
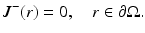
(21)
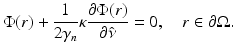
(22)
The boundary condition (22) can be extended to include the reflection on the boundary that is caused by different refractive indices between the object and the surrounding medium. In that case, Eq. 21 is modified to the form
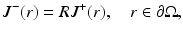
where R = R(x) is the reflection coefficient on the boundary 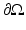 , with 0 ≤ R ≤ 1 [57]. Thus, if R = 0, no boundary reflection occurs, and Eq. 23 is reduced into Eq. 21. The parameter R can be derived from Fresnel’s law [40] or, if the refractive index of the surrounding medium is n out = 1, by an experimental fit
, with 0 ≤ R ≤ 1 [57]. Thus, if R = 0, no boundary reflection occurs, and Eq. 23 is reduced into Eq. 21. The parameter R can be derived from Fresnel’s law [40] or, if the refractive index of the surrounding medium is n out = 1, by an experimental fit
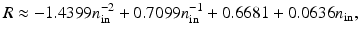
where n in is the refractive index of the medium [87]. Utilizing Eqs. 19 and 20 and the Fick’s law (15), the Robin boundary condition with mismatched refractive indices can be derived. It takes the form
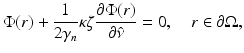
where ζ = (1 + R)∕(1 − R), with ζ = 1 in the case of no surface reflection. The boundary conditions of the DA for an interface between two highly scattering materials have been discussed, for example, in [4].
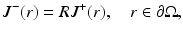
(23)
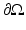 , with 0 ≤ R ≤ 1 [57]. Thus, if R = 0, no boundary reflection occurs, and Eq. 23 is reduced into Eq. 21. The parameter R can be derived from Fresnel’s law [40] or, if the refractive index of the surrounding medium is n out = 1, by an experimental fit
, with 0 ≤ R ≤ 1 [57]. Thus, if R = 0, no boundary reflection occurs, and Eq. 23 is reduced into Eq. 21. The parameter R can be derived from Fresnel’s law [40] or, if the refractive index of the surrounding medium is n out = 1, by an experimental fit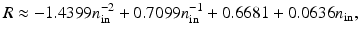
(24)
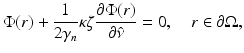
(25)
Source Models for the DA
In the DA framework, light sources are usually modeled by two approximate models, namely, the collimated source model and the diffuse source model. In the case of the collimated source model , the source is modeled as an isotropic point source
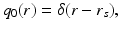
where position r s is located at a depth 1∕μ s ′ below the source site [40, 87]. In the case of the diffuse source model, the source is modeled as an inward-directed diffuse boundary current I s at the source position 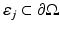 [87]. In the case of the diffuse source model, Eq. 23 can be modified as
[87]. In the case of the diffuse source model, Eq. 23 can be modified as
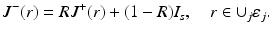
Then, following the similar procedure as earlier, the Robin boundary condition with the diffuse source model is obtained. It is of the form
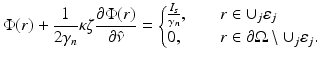
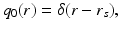
(27)
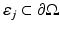 [87]. In the case of the diffuse source model, Eq. 23 can be modified as
[87]. In the case of the diffuse source model, Eq. 23 can be modified as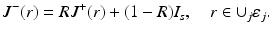
(28)
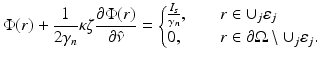
(29)
Validity of the DA
The basic condition for the validity of the DA is that the angular distribution of the radiance is almost uniform. In order to achieve this, the medium must be scattering dominated; thus, μ a ≪ μ s . Most of the tissue types are highly scattering and the DA can be regarded as a good approximation for modeling light propagation within them. The DA has been found to describe light propagation with a good accuracy in situations in which its assumptions are valid [63, 80] and it has been successfully applied in many applications of optical tomography.
However, the condition stating that the angular distribution of the radiance must be almost uniform is violated close to the highly collimated light sources. In addition, the condition cannot be fulfilled in strongly absorbing or low-scattering tissues such as the cerebrospinal fluid which surrounds the brain and fills the brain ventricles. Furthermore, in addition to the above conditions, the DA cannot accommodate realistic boundary conditions or discontinuities at interfaces. The diffusion theory has been found to fail in situations in which its approximations are not valid such as close to the sources [35, 87] and within the low-scattering regions [37, 48].
Numerical Solution Methods for the DA
The analytical solutions of the RTE and its approximations are often restricted to certain specific geometries, and therefore, their exploitability in optical imaging is limited. Therefore, the equations describing light propagation are usually solved with numerical methods. The most often applied numerical methods are the finite difference method and the finite element method (FEM). The latter is generally regarded as more flexible when issues of implementing different boundary conditions and handling complex geometries are considered, and therefore, it is most often chosen as the method for solving equations governing light transport in tissues.
Hybrid Approaches Utilizing the DA
To overcome the limitations of the diffusion theory close to the light sources and within low-scattering and non-scattering regions, different hybrid approaches and approximate models have been developed.
The hybrid Monte Carlo diffusion method was developed to overcome the limitations of the DA close to the light sources. In the approach, Monte Carlo simulation is combined with the diffusion theory. The method was introduced in [98] to describe light reflectance in a semi-infinite turbid medium, and it was extended for turbid slabs in [97]. In the hybrid Monte Carlo diffusion approach , Monte Carlo method is used to simulate light propagation close to the light source and the DA is analytically solved elsewhere in the domain. Monte Carlo is known to describe light propagation accurately. However, it has the disadvantage of requiring a long computation time. This has effects on computation times of the hybrid Monte Carlo approaches as well. A hybrid radiative transfer–diffusion model to describe light propagation in highly scattering medium was introduced in [93]. In the approach, light propagation is modeled with the RTE close to the light sources, and the DA is used elsewhere in the domain. The solution of the RTE is used to construct a Dirichlet boundary condition for the DA on a fictitious interface within the object. Both the RTE and the DA are numerically solved with the FEM.
Different hybrid approaches and approximate models have been applied for highly scattering media with low-scattering and non-scattering regions. Methods that combine Monte Carlo simulation with diffusion theory have been applied for turbid media with low-scattering regions. The finite element approximation of the DA and the Monte Carlo simulation was combined in [41] to describe light propagation in a scattering medium with a low-scattering layer. However, also in this case, the approach suffers from the time-consuming nature of the Monte Carlo methods. Moreover, the hybrid Monte Carlo diffusion methods often require iterative mapping between the models which increases computation times even more. The radiosity–diffusion model [10, 37] can be applied for highly scattering media with non-scattering regions. The method uses the FE solution of the DA to model light propagation within highly scattering regions and the radiosity model to model light propagation within non-scattering regions. A coupled transport and diffusion model was introduced in [18]. In the model, the transport and diffusion models are coupled, and iterative mapping between the models is used for the forward solution. Furthermore, a coupled radiative transfer equation and diffusion approximation model for optical tomography was introduced in [94] and extended for domains with low-scattering regions in [92]. In the approach, the RTE is used as the forward model in sub-domains in which the assumptions of the DA are not valid and the DA is used elsewhere in the domain. The RTE and DA are coupled through boundary conditions between the RTE and DA sub-domains and solved simultaneously using the FEM.
Green’s Functions and the Robin to Neumann Map
Some insight into light propagation in diffusive media can be gained by examining infinite media. In particular, verification of optical scattering and absorption parameters is frequently made with source and detector fibers immersed in a large container and far from the container walls. In a finite domain, however, we will need to use boundary conditions. We will distinguish between solutions to the homogeneous equation with inhomogeneous boundary conditions and the inhomogeneous equation with homogeneous boundary conditions. In the latter case, we can use a Green’s function acting on q 0. In the former case, we use a Green’s function acting on a specified boundary function.
We will use the notation 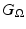 for the Green’s function for the inhomogeneous form of (18) with homogeneous boundary conditions and
for the Green’s function for the inhomogeneous form of (18) with homogeneous boundary conditions and 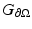 for the Green’s function for the homogeneous form of (18) with inhomogeneous boundary conditions, i.e., we have
for the Green’s function for the homogeneous form of (18) with inhomogeneous boundary conditions, i.e., we have 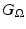 solving
solving
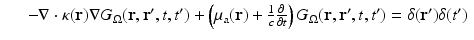
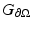 solving
solving
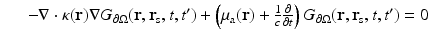
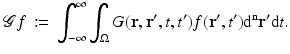 For the measureable, we define the boundary derivative operator as
For the measureable, we define the boundary derivative operator as
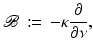 where appropriate we will use the simplifying notation
where appropriate we will use the simplifying notation
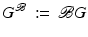 to mean the result of taking the boundary data for a Green’s function.
to mean the result of taking the boundary data for a Green’s function.

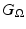 for the Green’s function for the inhomogeneous form of (18) with homogeneous boundary conditions and
for the Green’s function for the inhomogeneous form of (18) with homogeneous boundary conditions and 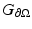 for the Green’s function for the homogeneous form of (18) with inhomogeneous boundary conditions, i.e., we have
for the Green’s function for the homogeneous form of (18) with inhomogeneous boundary conditions, i.e., we have 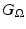 solving
solving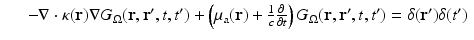
(30)
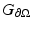 solving
solving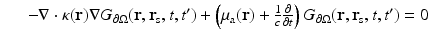
(32)
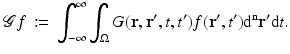
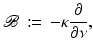
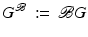
Since (18) is parabolic, we must not simultaneously specify both Dirichlet and Neumann boundary conditions on the whole of 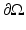 . The same is true if we convert to the frequency domain and use a complex elliptic equation to describe the propagation of the Fourier transform of
. The same is true if we convert to the frequency domain and use a complex elliptic equation to describe the propagation of the Fourier transform of 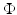 . Instead, we specify their linear combination through the Robin condition (25). Then, for any specified value q on
. Instead, we specify their linear combination through the Robin condition (25). Then, for any specified value q on 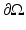 , we will get data y given by (26). The linear mapping
, we will get data y given by (26). The linear mapping 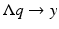 is termed the Robin to Neumann map and can be considered the result of a boundary derivative operator
is termed the Robin to Neumann map and can be considered the result of a boundary derivative operator 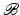 acting on the Green’s operator with kernel
acting on the Green’s operator with kernel 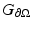
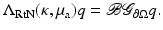 Since the Neumann data and Dirichlet data are related by (25), we may also define the Robin to Dirichlet map
Since the Neumann data and Dirichlet data are related by (25), we may also define the Robin to Dirichlet map 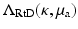 and specify the relationship
and specify the relationship
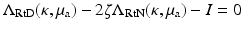
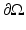 . The same is true if we convert to the frequency domain and use a complex elliptic equation to describe the propagation of the Fourier transform of
. The same is true if we convert to the frequency domain and use a complex elliptic equation to describe the propagation of the Fourier transform of 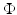 . Instead, we specify their linear combination through the Robin condition (25). Then, for any specified value q on
. Instead, we specify their linear combination through the Robin condition (25). Then, for any specified value q on 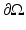 , we will get data y given by (26). The linear mapping
, we will get data y given by (26). The linear mapping 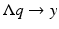 is termed the Robin to Neumann map and can be considered the result of a boundary derivative operator
is termed the Robin to Neumann map and can be considered the result of a boundary derivative operator 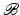 acting on the Green’s operator with kernel
acting on the Green’s operator with kernel 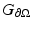
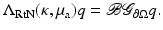
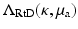 and specify the relationship
and specify the relationship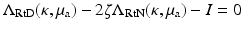
(34)
The Forward Problem
The Robin to Neumann map is a linear operator mapping boundary sources to boundary data. For the inverse problem, we have to consider a nonlinear mapping from the space of μ a, κ coefficients to the boundary data.
When considering an incoming flux J − with corresponding boundary term q, the data is a function of one variable
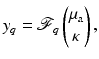
which gives the boundary data for the particular source term 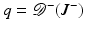 . Using this notation, we consider the forward mapping for a finite number of sources
. Using this notation, we consider the forward mapping for a finite number of sources 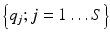 as a parallel set of projections
as a parallel set of projections
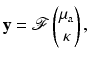
where
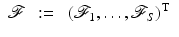
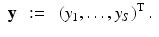
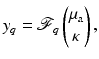
(35)
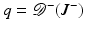 . Using this notation, we consider the forward mapping for a finite number of sources
. Using this notation, we consider the forward mapping for a finite number of sources 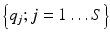 as a parallel set of projections
as a parallel set of projections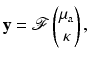
(36)
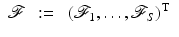
(37)
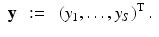
(38)
We will consider (36) as a mapping from two continuous functions in solution space 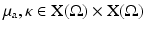 to continuous functions in data space
to continuous functions in data space 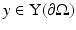 . If the data is sampled as well (which is the case in practice), then
. If the data is sampled as well (which is the case in practice), then  is sampled at a set of measurement positions
is sampled at a set of measurement positions 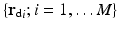 .
.
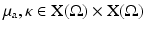 to continuous functions in data space
to continuous functions in data space 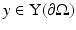 . If the data is sampled as well (which is the case in practice), then
. If the data is sampled as well (which is the case in practice), then  is sampled at a set of measurement positions
is sampled at a set of measurement positions 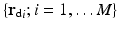 .
.The inverse problem of diffusion-based optical tomography (DOT) is to determine κ, μ a from the values of y for all incoming boundary distributions q. If κ, μ a are found, we can determine μ s ′ through (16).
Schrödinger Form
Problem (17) can be put into Schrödinger form using the Liouville transformation. We make the change of variables 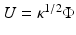 , by which (17) becomes
, by which (17) becomes
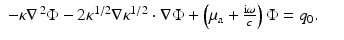 Using
Using
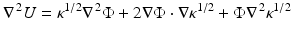 leads to
leads to
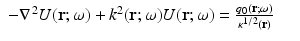
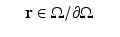
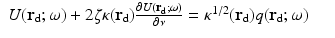
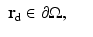
where
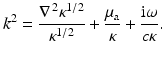 If k 2 is real (i.e., ω = 0), there exist infinitely many κ, μ a pairs with the same real k 2, so that the measurement of DC data cannot allow the separable unique reconstruction of κ and μ a [6]. For ω ≠ 0, the unique determination of a complex k 2 should be possible by extension of the uniqueness theorem of Sylvester and Uhlmann [91]. From the complex k 2, it is in principle possible to obtain separable reconstruction of first κ from the imaginary part of k 2 and μ a from the real part; see [74] for further discussion.
If k 2 is real (i.e., ω = 0), there exist infinitely many κ, μ a pairs with the same real k 2, so that the measurement of DC data cannot allow the separable unique reconstruction of κ and μ a [6]. For ω ≠ 0, the unique determination of a complex k 2 should be possible by extension of the uniqueness theorem of Sylvester and Uhlmann [91]. From the complex k 2, it is in principle possible to obtain separable reconstruction of first κ from the imaginary part of k 2 and μ a from the real part; see [74] for further discussion.
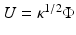 , by which (17) becomes
, by which (17) becomes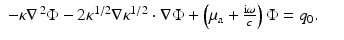
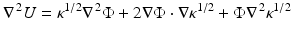
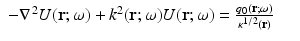
(39)
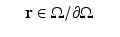
(40)
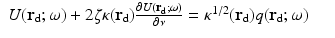
(41)
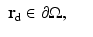
(42)
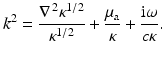
In a homogeneous medium, with constant optical parameters μ a, κ, we can simplify (42) to
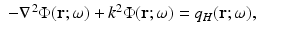
with the same boundary condition (25) and with
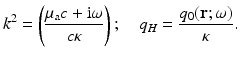
This equation is also seen directly from (17) for constant κ.
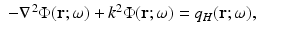
(43)
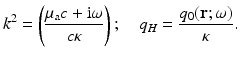
(44)
The solution in simple geometries is easily derived using the appropriate Green’s functions [8]. In an infinite medium, this is simply a spherical wave
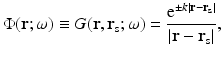
where the notation G(r, r s; ω) defines Green’s function for a source at position r s. Due to the real part of the wave number ky, this wave is damped. This fact is the main reason that results from diffraction tomography are not always straightforwardly applicable in optical tomography. In particular, for the case ω = 0, the wave is wholly non-propagating. Even as 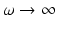 , the imaginary part of the wave number never exceeds the real part. This is a simple consequence of the parabolic nature of the diffusion approximation. Although hyperbolic approximations can be made too, they do not ameliorate the situation.
, the imaginary part of the wave number never exceeds the real part. This is a simple consequence of the parabolic nature of the diffusion approximation. Although hyperbolic approximations can be made too, they do not ameliorate the situation.
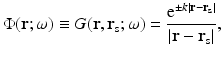
(45)
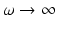 , the imaginary part of the wave number never exceeds the real part. This is a simple consequence of the parabolic nature of the diffusion approximation. Although hyperbolic approximations can be made too, they do not ameliorate the situation.
, the imaginary part of the wave number never exceeds the real part. This is a simple consequence of the parabolic nature of the diffusion approximation. Although hyperbolic approximations can be made too, they do not ameliorate the situation. Perturbation Analysis
An important tool in scattering problems in general is the approximation of the change in field due to a change in state, developed in a series based on known functions for the reference state. There are two common approaches which we now discuss.
Born Approximation
For the Born approximation, we assume that we have a reference state 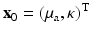 , with a corresponding wave
, with a corresponding wave 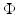 , and that we want to find the scattered wave
, and that we want to find the scattered wave 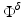 due to a change in state
due to a change in state 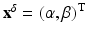 . We have
. We have
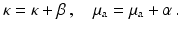
Note that it is not necessary to assume that the initial state is homogeneous. Putting (46) into (17) gives
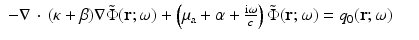
with
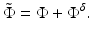
Equation 47 can be solved using the Green’s operator for the reference state
![$$\displaystyle{ \tilde{\Phi } = \mathcal{G}_{0}\left [q_{0} + \nabla \,\cdot \,\beta \nabla \tilde{\Phi } -\alpha \tilde{ \Phi }\right ]. }$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_Equ50.gif)
With G 0, Green’s function for the reference state, we have
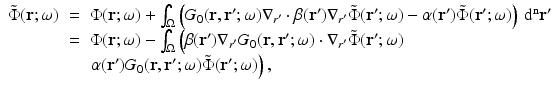
where we used the divergence theorem and assumed 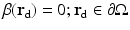 .
.
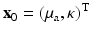 , with a corresponding wave
, with a corresponding wave 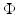 , and that we want to find the scattered wave
, and that we want to find the scattered wave 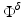 due to a change in state
due to a change in state 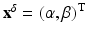 . We have
. We have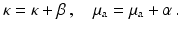
(46)
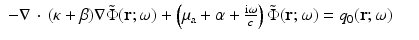
(47)
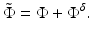
(48)
![$$\displaystyle{ \tilde{\Phi } = \mathcal{G}_{0}\left [q_{0} + \nabla \,\cdot \,\beta \nabla \tilde{\Phi } -\alpha \tilde{ \Phi }\right ]. }$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_Equ50.gif)
(49)
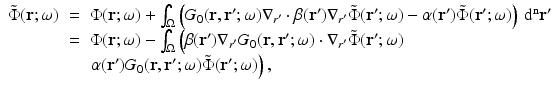
(50)
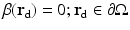 .
.Rytov Approximation
The Rytov approximation is derived by considering the logarithm of the field as a complex phase [54, 60]:
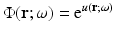
so that, in place of (48), we have
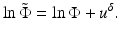
Putting 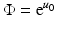 into (17), we get
into (17), we get
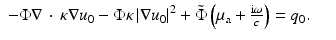
Putting 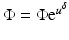 and (46) into (17), we get
and (46) into (17), we get
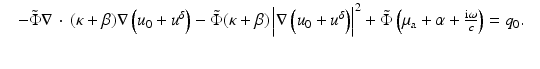
Subtracting (57) from (58) and assuming 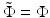 over the support of q 0, we get
over the support of q 0, we get
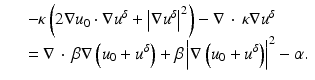
We now make use of the relation
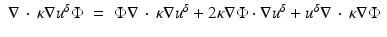
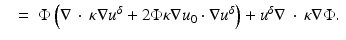
The last term on the right is substituted from (17) to give
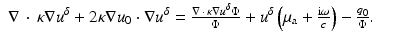
Substituting (62) into (59) and using
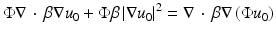 we arrive at
we arrive at
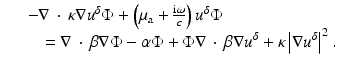
The approximation comes in neglecting the last two terms on the right, which are second order in the small perturbation. The left-hand side is the unperturbed operator, and so the formal solution for 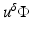 is again obtained through Green’s operator with kernel G 0. Thus, the first-order Rytov approximation becomes
is again obtained through Green’s operator with kernel G 0. Thus, the first-order Rytov approximation becomes
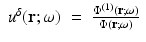
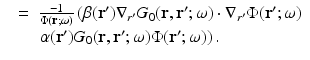
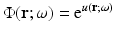
(55)
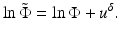
(56)
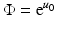 into (17), we get
into (17), we get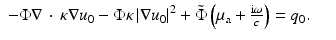
(57)
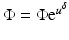 and (46) into (17), we get
and (46) into (17), we get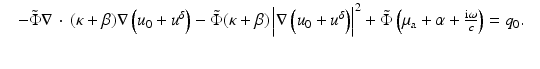
(58)
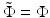 over the support of q 0, we get
over the support of q 0, we get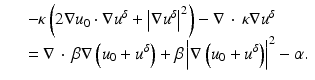
(59)
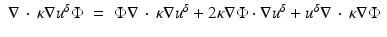
(60)
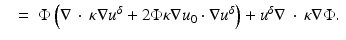
(61)
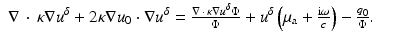
(62)
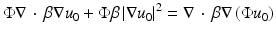
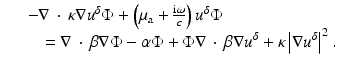
(63)
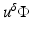 is again obtained through Green’s operator with kernel G 0. Thus, the first-order Rytov approximation becomes
is again obtained through Green’s operator with kernel G 0. Thus, the first-order Rytov approximation becomes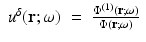
(64)
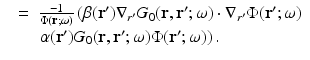
(65)
The Rytov approximation is usually argued to be applicable for larger perturbations than the Born approximation, since the neglected terms are small as long as the gradient of the field is slowly varying. See [60] for a much more detailed discussion.
Illustrations of the scattered field in the Born and Rytov formulations are shown in Fig. 2. Since in the frequency domain the field is complex, so is its logarithm. The real part corresponds to the log of the field amplitude and its imaginary part to the phase. From the images in Fig. 2, it is apparent that perturbations are more readily detected in amplitude and phase than in the field itself. This stems from the very high dynamic range of data acquired in optical tomography which in turn stems from the high attenuation and attendant damping. It is the primary motivation for the use of the Rytov approximation, despite the added complications.

Get Clinical Tree app for offline access

Fig. 2
Top: absorption and scattering images used to generate complex fields. Disk diameter 50 mm, absorption range ![$$\mu _{{\mathrm{a}}} \in [0.01\mbox{ \textendash }0.04]\,{\mathrm{mm}}^{-1}$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_IEq59.gif) , scatter range
, scatter range ![$$\mu _{{\mathrm{s}}}^{{\prime}}\in [1\mbox{ \textendash }4]\,{\mathrm{mm}}^{-1}$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_IEq60.gif) . The complex field
. The complex field 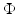 was calculated using a 2D FEM for a δ-function source on the boundary at the 3 o’clock position. A reference field
was calculated using a 2D FEM for a δ-function source on the boundary at the 3 o’clock position. A reference field 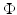




![$$\mu _{{\mathrm{a}}} \in [0.01\mbox{ \textendash }0.04]\,{\mathrm{mm}}^{-1}$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_IEq59.gif) , scatter range
, scatter range ![$$\mu _{{\mathrm{s}}}^{{\prime}}\in [1\mbox{ \textendash }4]\,{\mathrm{mm}}^{-1}$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_IEq60.gif) . The complex field
. The complex field 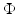 was calculated using a 2D FEM for a δ-function source on the boundary at the 3 o’clock position. A reference field
was calculated using a 2D FEM for a δ-function source on the boundary at the 3 o’clock position. A reference field 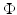
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



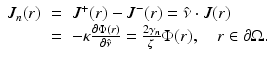
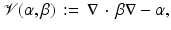
![$$\displaystyle{ \left [{\mathsf{I}} -\mathcal{G}_{0}\mathcal{V}\right ]\tilde{\Phi } = \mathcal{G}_{0}q_{0}. }$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_Equ53.gif)
![$$\displaystyle{ \frac{\mathcal{G}_{0}} {\left [{\mathsf{I}} -\mathcal{G}_{0}\mathcal{V}\right ]} = \mathcal{G}_{0} + \mathcal{G}_{0}\mathcal{V}\mathcal{G}_{0} + \mathcal{G}_{0}\mathcal{V}\mathcal{G}_{0}\mathcal{V}\mathcal{G}_{0} + \cdots }$$](/wp-content/uploads/2016/04/A183156_2_En_21_Chapter_Equ54.gif)