Magnetic resonance imaging (MRI) is based on spatially encoding a nuclear magnetic resonance (NMR) signal. Therefore an understanding of the basics of NMR is critical for understanding MRI, and this information is given in the first section of this chapter. Magnetic field gradients are used in MRI to spatially encode the NMR signal to obtain the raw MRI data, or k-space. Images are reconstructed from k-space using mathematical algorithms, most commonly the Fourier transform. Image contrast is controlled by changing the timings of the encoding using specific pulse sequences. Thus in addition to a basic explanation of NMR signal generation, the process of spatial encoding and contrast generation are described. Additionally, commonly used rapid imaging techniques and frequently encountered artifacts are introduced.
Physics Principles
Nuclear Spin
All atoms are made up of electrons surrounding an atomic nucleus, which can contain protons and neutrons. The nucleus of an atom can have a quantum property known as nuclear spin. For instance, a hydrogen atom has a proton as its nucleus, and the magnetization from a macroscopic sample of proton spins is what is commonly measured in NMR and MRI. Many other atoms have nuclei with this property, but the discussion here will focus on hydrogen nuclei (i.e., protons) because hydrogen is a key component of biological tissue (e.g., water, fat) and most commonly visualized in clinical MRI.
The behavior of each individual nucleus is described by quantum mechanics. However, when working with many nuclei in bulk, the picture can be simplified to make it more easily understandable. In this treatment the magnetization from a single proton can be thought of as an arrow pointing in a specific direction in three-dimensional (3D) x-y-z space. In the absence of an externally applied magnetic field, the nuclear magnetization is randomly oriented; in other words the magnetization from each proton in a group of protons (i.e., in a cup of water or the human body) is not aligned. If one were to try to measure the net magnetization or aggregate magnetization coming from the group of protons, it would be zero because each arrow would be pointing in a different direction, resulting in total cancellation.
However, in the presence of an external magnetic field such as that used in NMR or MRI, the nuclei act like tiny bar magnets and align themselves with the field in one of two states—parallel or antiparallel. If an equal number of protons were in each state, the net magnetization would again be zero (the magnetic field from the nuclei pointing up would cancel the field from the nuclei pointing down). However, the state parallel to the external magnetic field has a slightly lower energy level than the antiparallel state, so slightly more nuclei end up in the parallel state than in the antiparallel state. This small difference in parallel and antiparallel protons leads to the signal used for imaging in MRI. For clinical MRI field strengths, only one or two protons in a million can be detected; this number increases as the MRI field strength increases (which leads to an increase in the signal-to-noise ratio [SNR] at higher field strengths). The net magnetization, or magnetization from these excess protons, can be visualized as a larger arrow pointing in the direction of the external magnetic field, where the size of the arrow indicates the magnitude of the magnetization.
Nuclear Magnetic Resonance
The net magnetization of protons in an external magnetic field aligns with the external magnetic field. This is called the equilibrium state of the magnetization and is usually defined as the z-direction ( Fig. 3-1A [red arrow] ). However, by applying energy in the form of electromagnetic waves at precisely the right frequency, the net magnetization can be made to tip away from the equilibrium position into the x-y plane. This frequency is known as the Larmor frequency:
ω = γ B 0
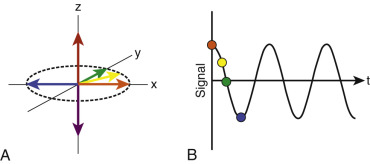
Signal can only be picked up from magnetization that is precessing in the x-y plane. An RF receiver coil is used to collect the signal after it is tipped into this plane using an RF pulse. In simple terms the receiver coil “sees” magnetization along one direction; in other words, voltage is induced in the receiver coil because of the change in direction of the magnetization vector that results from the precession (similar to an electrical generator). To demonstrate the relationship between the precession of the magnetization and the signal, the x-direction will be used as an example here. When the magnetization is pointed toward the x-axis, the signal will be at a maximum (see Fig. 3-1B [orange dot] ). When the magnetization precesses to be completely on the y-axis, there is no magnetization in the x-direction, so the signal picked up by the receiver coil is zero (see Fig. 3-1B [green dot] ). When the magnetization precesses further into the −x direction, the signal will have a minimum (see Fig. 3-1B [blue dot] ). The signal over time seen by precessing magnetization traces out a sinusoid, which can be appreciated in Figure 3-1 . This treatment ignores relaxation, which is discussed next.
Relaxation
The net magnetization in an external static magnetic field aligns with the magnetic field, but an RF pulse can be used to tip this magnetization into the x-y plane as explained earlier. Once tipped and with no further perturbation, the magnetization returns to the equilibrium state along the z-axis. This return to the equilibrium state is known as T1 relaxation, otherwise known as spin-lattice relaxation or longitudinal relaxation. T1 relaxation follows an exponential recovery curve, as shown in Figure 3-2A , which is described by the following equation (assuming the signal started in the x-y plane after a 90-degree RF pulse):
s ( t ) = 1 − e − t / T 1
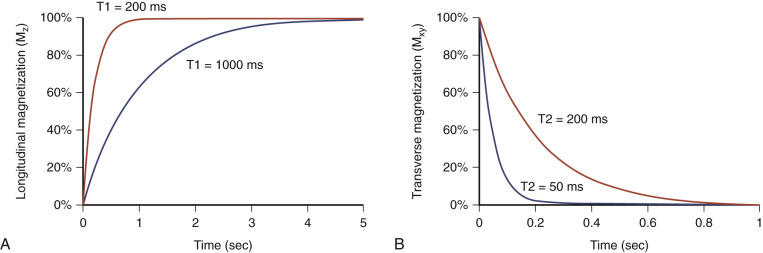
In addition to T1 relaxation, a second relaxation mechanism is often used to impart contrast to MRI. This second relaxation parameter is T2 relaxation, otherwise known as spin-spin or transverse relaxation. The T2 parameter describes the behavior of the magnetization as it precesses in the x-y plane. Recall that the net magnetization is actually a sum of the magnetization of many protons. If all the protons precess at exactly the same frequency, the net magnetization would retain the same magnitude as it precesses. However, if some of these spins precess at slightly higher frequencies (i.e., a bit faster) and some at slightly lower frequencies (i.e., a bit slower), the magnetization will begin to “fan out” in the x-y plane. The net sum of this fanned out magnetization will have a smaller magnitude than when all the spins precess at exactly the same frequency. Over time the slight differences in precession frequency will lead to magnetization that is spread in all directions in the x-y plane, leading to a net magnetization of 0. This T2 relaxation process is described using the following equation:
s ( t ) = 1 − e − t / T2
The smaller the T2 value, the faster the magnetization fans out around the x-y plane, leading to a rapid decrease in the signal (see Fig. 3-2B ). Like T1, different tissues have different T2 values depending on the makeup of the tissue. Small disturbances in the local magnetic field of the tissue can cause rapid T2 decay as well as differences in the chemical environments. In a broad sense, T2 provides information about how fluidlike a particular tissue is; solid tissues have shorter T2 values, whereas pure liquid water has a very long T2 value. It is important to note that the T1 and T2 times of tissues are not mathematically related, and MRIs are often weighted by one (or both) of these parameters to highlight desired structures. However, T2 is always shorter than T1.
Although the T2 value is an intrinsic tissue property, the transverse magnetization can also be affected by small differences in the magnetic field. Any inhomogeneities in the field will cause individual nuclei to have slightly different resonance frequencies and lead to a more rapid fanning out of the magnetization in the x-y plane. The parameter that describes the relaxation of magnetization in the transverse plane secondary to field inhomogeneities is T2*. The actual T2* depends on the local magnetic field, which can be affected by differences in magnetic susceptibility of adjacent materials (i.e., tissue-air interfaces) or the presence of iron. T2* is always shorter than T2, and although T2 relaxation cannot be avoided, the effects of T2* relaxation can be eliminated by using some specialized imaging techniques (e.g., spin echo sequences).
Chemical Shift
So far it has been assumed that all protons have the same precession frequency, also called the resonance frequency. However, the Larmor equation actually only describes the resonance frequency of an isolated hydrogen nucleus. The proton is almost never found completely isolated; hydrogen is normally bound to another nucleus (in water, this is oxygen) through chemical bonds. These chemical bonds are made up of electrons moving around the nuclei of the bound atoms, and this cloud of electrons serves to “shield” the protons of the hydrogen atom from the externally applied main magnetic field. Thus the actual magnetic field seen by the protons is usually slightly less than the actual applied field, as described in the following equation:
ω c = γ ⋅ ( 1 − σ ) B
The Basic NMR Experiment
The basic concepts described can be put together to understand how a simple hydrogen NMR experiment works. The timing of the events in the experiment is described using a pulse sequence diagram, where each line represents a different type of event. The basic NMR pulse sequence diagram in Figure 3-3 shows when RF pulses are applied (top) and when data are collected (bottom).
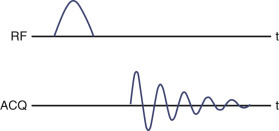
A sample made up of substances containing protons is placed in an NMR scanner with a strong external magnetic field, B 0 . This field causes the protons to align, leading to a net magnetization. An RF pulse is applied to tip the magnetization from the equilibrium z-axis into the x-y plane. Once in the x-y plane the magnetization begins to precess at a frequency determined by the chemical environment of the hydrogen nuclei. Signal from this precessing magnetization is collected using a receiver coil. During signal collection the magnetization experiences both T1 and T2 relaxation simultaneously. The precession causes the signal to oscillate, and the relaxation causes the signal to decay to zero, leading to an overall signal form that looks like an exponentially decaying sinusoid (this shape is shown on the data acquisition line labeled “ACQ” in Fig. 3-3 ). This process can be repeated several times and the signal averaged to increase the SNR (see “ Imaging Time and Performance Tradeoffs ”).
Such an experiment can be used to determine how many and what type of chemical compounds are present in a sample by examining the resonance frequencies in the collected signal. However, because the receiver coil picks up signal from all parts of the sample, there is no information about the spatial distribution of the chemical compounds in the sample.
Imaging
Introduction
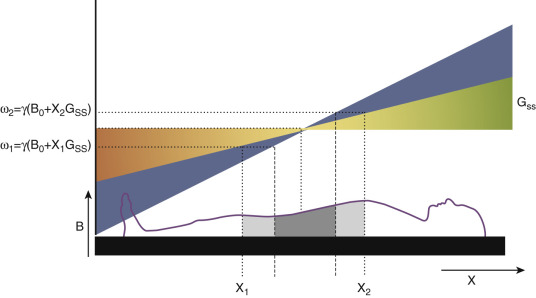
NMR is traditionally used to determine the chemical structure of a sample and does not require spatial localization. However, MRI depends on being able to distinguish between spins at different physical locations, so spatial localization is performed by applying magnetic field gradients in each of the three spatial axes in addition to the main static magnetic field. A schematic of this idea is shown for one-dimensional (1D) encoding in Figure 3-4 . Although this picture does not fully explain how two-dimensional (2D) or 3D spatial localization is performed, this idea forms the basis for spatial encoding in MRI, which will be explained in detail in the following sections.
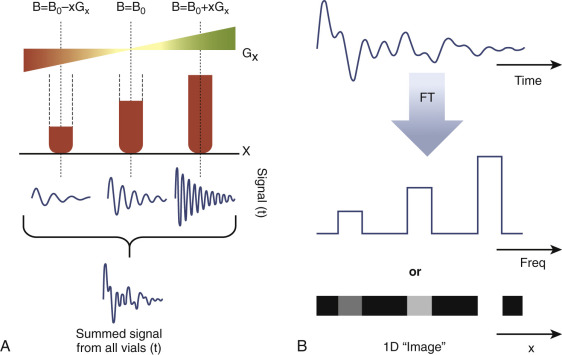
In Figure 3-4A , three signal sources (liquid in tubes) are shown in red. Here a linearly varying magnetic field is applied in the x-direction; this field gradient is called G x . At the center the amplitude of this additional magnetic field is 0, and the spins at that location precess at the Larmor frequency determined by the main magnetic field. However, the spins on the left side experience a total magnetic field that is slightly less than the main magnetic field owing to the gradient. These spins will precess with a slightly lower frequency. Similarly the spins on the right side experience a slightly higher magnetic field and precess at a slightly higher frequency. Thus the result of applying this magnetic field gradient is to differentiate spins at different locations by causing them to precess at different frequencies. In this way a one-to-one mapping can be made that links the location of the spins to their frequency. Additionally, note that the left-most vial contains less fluid and the signal coming from this vial has a lower amplitude than the center vial, which also has a lower amplitude than the right-most vial. In fact the signal amplitude at each frequency is directly proportional to the number of spins precessing at that frequency. The signals coming from the different locations, however, cannot be separated by the receiver coil. Only the sum of the three signals is actually collected. This signal is shown at the bottom of Figure 3-4A , and the next section describes how image information is derived from this composite signal.
Data to Image: Fourier Transform
The schematic shown in Figure 3-4A and the legend explain how spatial encoding is performed but do not explain how spatial information is extracted from the signal to form an image in MRI. As described earlier the MRI signal is collected from the entire volume using a receiver coil. Thus the challenge is to separate individual single frequency signals from the complex multifrequency data. Mathematics has a simple way to perform this separation: the Fourier transform, which decomposes a signal in time into its component frequencies—exactly the problem that must be solved in MRI. By finding the Fourier transform of the MRI signal, a “map” of the frequencies contained by the signal can be derived. Because the frequencies correspond directly to the spatial locations of the spins, this frequency map is also equivalent to the 1D “image” of the spins. Note that in the 1D image shown in Figure 3-4B , the vial on the left with little liquid has a low signal intensity, the center vial a medium intensity, and the vial on the right a high intensity. All frequencies that were not present in the signal correspond to zeros in the frequency map and black in the 1D image.
Frequency Encoding
Nearly all MRI scans perform spatial localization in one dimension using frequency encoding, which is the closest form of encoding to the basic schematic shown in Figure 3-4 . In frequency (or read) encoding, a magnetic field gradient is applied to the object in one direction while data are collected (and hence the alternative name, read encoding ). The spins precess at a frequency dictated by their local magnetic field, and the resulting data are a complex combination of all of the different frequencies, as described earlier. If a 1D Fourier transform is applied to these data, a 1D projection through the object would result, as shown at the bottom of Figure 3-4B . Only one dimension can be resolved using frequency encoding, because the second dimension is not encoded and the spins in that direction are not distinguishable from one another. For this reason, another encoding mechanism must be employed in addition to frequency encoding, namely phase encoding.
Phase Encoding
Phase encoding works through the same basic mechanism as frequency encoding. The only difference is that the magnetic field gradient used in phase encoding is not applied while the data are being collected. Instead a phase-encoding gradient is turned on in a direction orthogonal to the readout direction before data collection. While the phase-encoding gradient is turned on, the spins precess with a frequency that depends on their spatial location ( Fig. 3-5A ). Once the gradient is turned off the spins will stop precessing, but they will retain the phase they had due to the phase-encoding gradient (hence the name). A readout gradient is then applied in the second encoding direction, as described earlier, and data are collected.
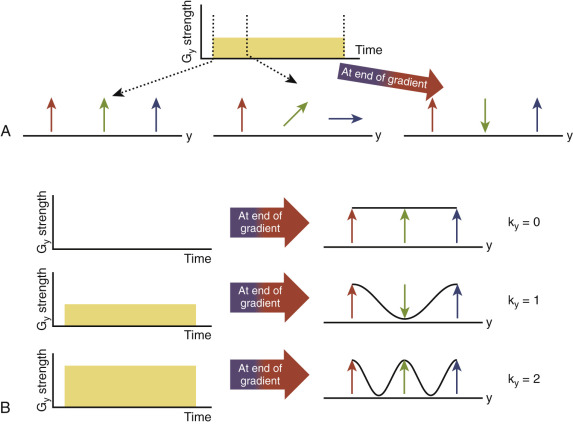
The application of one phase-encoding gradient would not help to make a 2D image, because just imparting a phase is not enough to spatially encode information. Thus many phase-encoding gradients with different strengths are applied, followed by a readout after each. The effect of applying phase-encoding gradients with different strengths is shown in Figure 3-5B . Here, schematic gradients are shown for k y = 0, k y = 1, and k y = 2. Note that the area of the gradient (time multiplied by amplitude) determines how much phase is accumulated across the field of view (FOV). If each readout line for different phase-encoding gradient magnitudes are collected and put into a 2D grid, the resulting data matrix is known as k-space.
k-Space
k-Space is the commonly used name for the raw data collected in MRI. These data are a set of sampled points stored in a matrix of numbers, where each line of numbers corresponds to one value of the phase-encoding gradient. The units of k-space are time (s) or inverse meters (m −1 ); both are different ways of looking at the same data. The k-space data are encoded as previously described, with phase and frequency encoding using magnetic field gradients. The gradients control the path that is traversed through k-space. An example of how gradients are used to “drive” through k-space is shown in Figure 3-6 . The phase-encoding gradient is used to move up and down in k-space, and the readout gradient is used to move to the left and right.
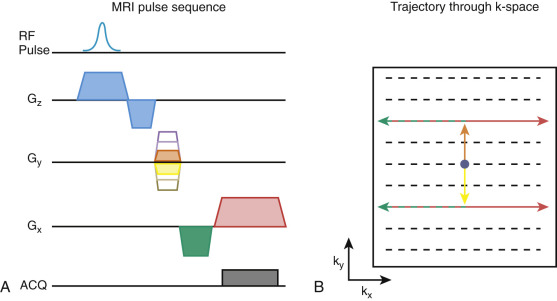
Once the k-space data have been collected, a discrete Fourier transform is applied to mathematically transform the data to the image domain. The Fourier transform takes the complex multifrequency data and reports back which frequencies are present in the data. The result is a matrix of numbers that correspond to the image. The units of the image are the inverse of the k-space data, namely inverse seconds (s −1 , or Hz) or meters (m), which matches with the idea that the image is a map of the frequencies generated using phase and frequency encoding as previously described.
Resolution and Field of View
The FOV is defined as the total size of the image (in units of distance). The matrix size of the image is often a power of 2 (128, 256, 512) owing to historical restrictions on performing a fast Fourier transform. Given the FOV and matrix size for an image, resolution is defined as the FOV divided by the matrix size, resulting in the nominal pixel or voxel size. For instance, if a 2D image has an FOV of 200 mm × 200 mm with a matrix size of 128 × 96 in the read and phase-encoding directions, the spatial resolution (pixel size) would be 1.56 mm × 2.08 mm in these directions.
The FOV and resolution of the image are directly related to the spacing and coverage of the data collected in k-space. The spacing between adjacent points in k-space determines the FOV in the image. The closer the phase-encoding lines or readout points are in k-space, the larger the FOV will be. In general the k-space spacing is chosen to be just large enough to cover the entire object. If the spacing between k-space lines becomes too large, the FOV may no longer cover the object, which can lead to aliasing artifacts (described in the “ Parallel Imaging ” and “ Clinical Artifacts ” sections).
The resolution of the image is determined by the extent of the k-space covered. The extent can be described by looking at the product of the spacing between k-space points (which determines the FOV) and the number of points collected. The larger this product is, the higher the image resolution will be. This relationship can be understood by thinking of the image as a frequency map. When more time-domain data (k-space) are collected, more frequencies can be resolved from that data, and the resolution of the image will be higher.
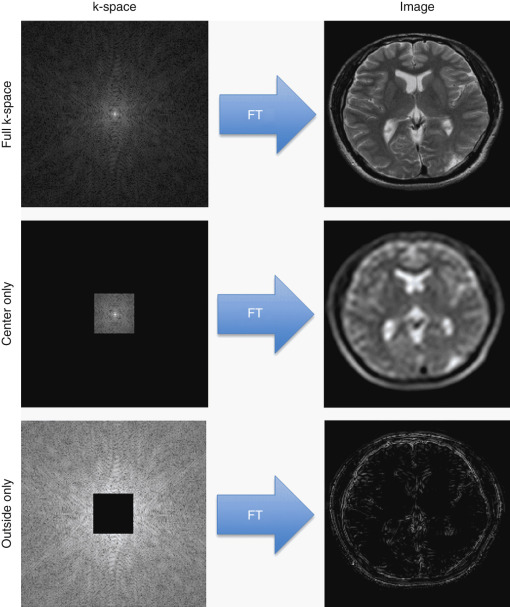
The significance of the different parts of k-space can be examined by removing some portions of data and performing a Fourier transform to see what happens in the resulting image. It is often said that the center of k-space determines the contrast of the image and the outer portions of k-space provide resolution. Figure 3-7 explores this statement by manipulating the k-space. At the top, an example k-space and its corresponding image is shown. If the extent of the k-space is reduced by eliminating some of the outer k-space lines, the resulting image has a lower spatial resolution (it appears blurrier [middle] ). If only the outer portions of k-space are retained and the central portions set to zero, only the edges appear in the image (bottom). The effects of eliminating other areas of k-space are examined later in “Fast Imaging for Clinical Practice.”
2D vs. 3D: Slice and Volumetric Encoding
Most clinical MRI images are collected in 2D, where the two spatial dimensions are encoded using read and phase encoding. However, before these dimensions can be encoded the desired 2D slice must be selected from the 3D volume of the body. This process is performed using slice-selection encoding.
Simultaneously with the RF excitation pulse, a slice-selection magnetic field gradient is applied to the subject in the slice direction (perpendicular to read and phase-encoding direction). The RF pulse will only excite magnetization resonating at specific frequencies. Because the resonance frequency can be controlled by application of the slice-select gradient, by setting the pulse sequence parameters correctly, only magnetization inside the desired slice will be excited by the RF pulse, and the magnetization outside the slice will remain mostly untouched. This process is shown schematically in Figure 3-8 . The excited magnetization will then be subjected to read and phase encoding to resolve the spatial information in the 2D slice.
As in read and phase encoding, a higher definition in the slice direction (or thinner slice) requires a stronger gradient in the slice direction. If the slice gradient is very weak, the slice will be very thick (light gray slice in Fig. 3-8 ). Such a thick slice can also be selected and then further encoded using a second, independent phase-encoding gradient in the slice direction. Such encoding is termed 3D encoding, and the second phase-encoding operation is often called partition encoding (to distinguish a 2D slice from a single 3D partition); 3D encoding results in a true 3D k-space, requiring a 3D Fourier transform to reconstruct the 3D image. Although 3D encoding is more time consuming, the image SNR is significantly higher because of the larger area covered. However, because the scan time is longer, there is a greater chance for image artifacts due to motion, which is why 3D imaging is used clinically less frequently than 2D imaging.
Pulse Sequences for MRI
Pulse sequences are methods for manipulating the magnetization of tissues and the signals they produce to generate a specific image contrast. An MRI system programmer uses pulse sequences to exploit the NMR principles that produce signal from tissue (and thus contrast among different tissues) and to perform spatial encoding.
The pulse sequence is a series of events triggered over time by the MRI scanner to change the magnetization of tissue in some way. There are two basic ways of manipulating the magnetization of tissue: applying RF energy and applying magnetic field gradients (G x , G y , and G z ). The pulse sequence diagram is a schematic that describes the order and duration of RF and gradient fields being switched on and off over time to produce the type of image contrast weighting and spatial encoding the MRI user wants. Each family of pulse sequences has strengths and weaknesses for different clinical imaging applications.
As described earlier the RF is switched on for a very short time with variable power and then switched off, and this short transmission is called an RF pulse. When it is used to excite the tissue signal for imaging, it is often called an excitation or flip pulse. For a specific MR scan the pulse will be associated with a flip angle that corresponds with the resulting magnetization of the excited tissue (0 degrees is magnetization parallel to the B 0 field, shown by the red arrow in Figure 3-1 , 90 degrees is perpendicular to B 0 , shown by the orange arrow, and 180 degrees is antiparallel to B 0 , shown by the purple arrow). Additional RF pulses may be applied at different times, depending on the type of pulse sequence.
Pulse Sequence Diagrams.
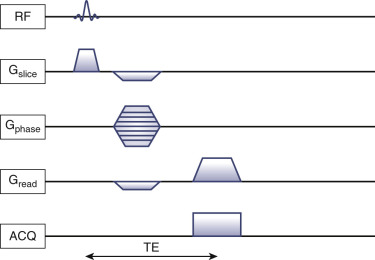
The pulse sequence diagram is an illustration of the time relationship of the different events that make up the pulse sequence. It is not always drawn to scale. There are some common symbols used in pulse sequence diagrams, but there is no standard format. Events in the pulse sequence are represented by symbols located on the respective line at the relative time of the event.
There are five essential system hardware functions whose events are usually shown on a pulse sequence diagram: RF, G slice , G phase , G read , and ACQ ( Fig. 3-9 ). Note that the pulse sequence shown in this figure is a gradient echo sequence, but the same basic elements appear in all pulse sequences. RF pulses are shown on an RF line to indicate any excitation and refocusing pulses. The three orthogonal magnetic field gradients, namely phase, slice, phase, and frequency (or read) encoding, are shown as separate lines. The activation of each of the gradients is indicated by a step change on the appropriate gradient’s line. The activation of the receiver and the data acquisition period (ACQ) is normally shown in context with the other elements of the pulse sequence. Sometimes the acquisition is shown in the same line as the RF pulses because this also represents an RF event.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree