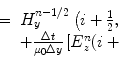Inclusion of A Priori Information Using Neural Networks

, Abas Sabouni², Travis Desell³ and Ali Ashtari⁴

(1)

Department of Electrical Engineering, University of North Dakota, Grand Forks, ND, USA

(2)

Department of Electrical Engineering, Wilkes University, Wilkes-Barre, PA, USA

(3)

Department of Computer Science, University of North Dakota, Grand Forks, ND, USA

(4)

Invenia Technical Computing, Winnipeg, MB, Canada

Abstract

Microwave image reconstruction is an ill-posed problem. Regularization methods are used to remove the ill-posed answers. However, the regularization methods are often problem independent and have smoothing effects. In this chapter, a novel problem-dependent regularization approach is introduced for the application of breast imaging that exploits a priori information for regularization. A real genetic algorithm (RGA) minimzes a cost functional that is essentially the error between the recorded and simulated data. At each iteration of the RGA, a neural network classifier rejects the solutions that cannot be a map of the dielectric properties of a breast. Although the application presented in this chapter is specific to breast cancer, the idea of using a priori information along with the classification techniques can be generally applied to the scenarios where information about the dielectric properties of the medium exists.

5.1 Hybrid GA Global Optimization and Neural Network Training

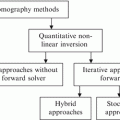
One of the problems with GA for solving the inverse scattering problem is that the GA operators do not assure that the chromosomes of the next generation are admissible solutions. In order to mitigate this problem, a training procedure is added to the optimization procedure. In this technique, the real genetic algorithm (RGA) for optimization and feedforward neural network (NN) for training the system have been applied [1]. This method will be referred to as neural network real-coded GA (NNRGA) throughout this chapter. In each RGA iteration, a priori information about the shape of the object profile is checked by an NN classifier to reject the solutions that cannot be a map of the dielectric properties of the object profile. Figure 5.1 shows the block diagram of the proposed technique with and without the NN block. Mainly, an NN classifier is applied to each individual which is created by the RGA, and any profile that does not “look like” an OI profile is disregarded. Therefore, we need to define the NN classified from a priori information about the OI. The main advantage of the NN is increasing the convergence rate. In fact, in the regular GA (RGA or BGA)/(FD)²TD technique, for any individual, the forward solver is running in order to calculate the fitness value, regardless of whether or not the temporary solution looks like an image for that specific application. Therefore, suitable genetic operators such as NN classifiers have to be defined in order to obtain admissible solutions and to enhance the convergence process. In the NNRGA technique, at each step, a new temporary population is generated applying the crossover, mutation, and elitism operator to ensure a monotonic decrease of the best fitness in the population during the iterative process, and then it goes to the NN evaluation procedure to check different features. If the temporary population meets the NN criteria, it will go to the next step which is the fitness-function calculation. Otherwise, the temporary population will be replaced with another one and go through the same procedure. The NN features have been extracted depending on the application beforehand.

Fig. 5.1

Block diagram of the RGA (a) without NN classifier and (b) with an NN classifier

Basically, the ill-posedness of the inverse problem creates many solutions for an inverse problem. By merging the NN procedure with the GA approach, the possible solutions decrease, and eventually the ill-posed condition for the inverse scattering problem decreases.

For example, for breast imaging application, 12 features are extracted for each profile in the search area such as the percentage of tissue in the fatty groups, the fibroglandular groups, the transitional group, and the total percentage of the fatty tissue. The number of connected fatty regions and connected fibroglandular regions are two additional features used for the classification. For more details about these features and how to extract them see [2]. The proposed technique was able to remove ill-posed answers without smoothing the reconstructed profile and also significantly decreased the computation runtime. This technique has been evaluated for four types of breasts and was able to reconstruct both high contrasts (between the fatty and the fibroglandular tissue) and low contrasts (between the fibroglandular tissue and the tumor). It should be noted that the method was able to provide a 4 mm resolution on realistic numerical breast phantoms [2].

5.2 Regularization Through Neural Network Classification

Microwave imaging has the potential to become a routine image modality in medicine. Microwave tomographically reconstructed images may potentially provide information about the tissue characteristics. The development of efficient inverse scattering algorithms and design and construction of effective measurement systems are the critical issues that have so far prevented the realization of commercial microwave imaging apparatus [3]. There has been a growing interest in the development of numerical codes for microwave imaging applications [4–6].

The ill-posedness of the inverse scattering problem is a major difficulty in the development of microwave imaging systems. Ill-posedness produces ill-conditioned matrices in numerical inversion methods. Regularization is used to tackle this issue. Different regularization approaches have been implemented in the microwave image reconstruction methods [7–13]. These regularization approaches have been applied to a wide range of applications including biomedical imaging [14], through-wall imaging [15], and mine detection [16].

Traditional regularization methods are mathematical methods that facilitate the inversion of ill-conditioned matrices and are application-independent. While being application-independent broadens the use of the traditional regularization methods for a variety of applications, it limits their effectiveness for specific applications. This is because the imaging medium is different in different applications and traditional regularization approaches do not make use of this fact. The possible distribution of the values of the dielectric properties of the imaging medium for any specific application has a certain range and shape. This information can be used to narrow the search space and to remove the ill-posed answers. In this chapter, a new regularization mechanism is proposed for our application of microwave breast imaging that uses a priori information of the breast tissue.

Traditional regularization methods usually “smoothen” the borders between the high-contrast and low-contrast regions. In the application of breast imaging, there is usually a high contrast between the dielectric properties of fatty and fibroglandular tissues. Tumors usually start to grow inside the fibroglandular tissue [17]. Therefore, smoothing effects make the detection of early-stage tumors very difficult because the contrast between the dielectric properties of fibroglandular tissue and cancer tissue is small [18]. Thus, early detection requires a regularization method that does not smoothen the profile and is able to reconstruct sharp contrasts. In other words, an ideal breast image reconstruction method should be able to handle the high contrast between the fatty and the fibroglandular tissue and the low contrast between the tumor and the fibroglandular tissue. Our proposed method is able to reconstruct both low and high contrasts based on the extensive use of a priori information.

The University of Wisconsin computational electromagnetics group (UWCEM) has made available a database [19] of anatomically realistic numerical breast phantoms that can be used in computational electromagnetics simulations. The database uses the information obtained in the comprehensive study of Lazebnik et al. [18] to characterize the dielectric properties of the breast tissue. The database contains different breast samples including mostly fatty, scattered fibroglandular, heterogeneously dense, and very dense samples. The database provides a realistic reference for testing the breast microwave imaging algorithms. It also provides extensive a priori information about the range and shape of the dielectric property distribution of the breast tissue. The proposed regularization method, which widely uses a priori information, has been made possible thanks to this study. For other microwave imaging applications, similar methods can be designed once enough a priori information about the imaging medium becomes available.

One example of a priori information that can be used in the reconstruction algorithms is the nonuniform distribution of the dielectric properties of the breast tissue. According to [18], the values of relative permittivity of the breast tissue at the frequency of 1 GHz can vary between 2.4 and 68.9. However, the values of the dielectric properties of the tissue are not distributed uniformly in that range. For example, only a small fraction of the dielectric properties of the breast tissue is between 7.5 and 37.2 which corresponds to the dielectric properties of the transitional tissue [19]. Therefore, a profile of dielectric properties that is made mainly from the transitional tissue cannot be a potential profile of a breast and should be removed from the search space. In other words, less computation time should be spent searching in the transitional tissue range. This is ignored in the traditional regularization methods.

Traditional microwave image reconstruction methods can be divided into two categories: local optimization methods [20–24] and global optimization methods [25–33]. Local optimization methods require rigorous regularization (which often results in smoothing effects) in order to escape the local minima. Global optimization methods can escape from local minima through randomization. Therefore, there is no need for global optimization-based inverse scattering methods to use the same regularization approaches as local optimization methods. Global optimization methods are more flexible regarding the regularization strategy. However, existing global optimization methods used for microwave image reconstruction mainly use the same regularization approaches as local optimization methods, i.e., they assume that sharp changes do not occur in the dielectric property profiles. The proposed method uses the flexibility of the global optimization methods with respect to the regularization approach, to define a new regularization approach.

The proposed method combines a neural network (NN) and an RGA and will be referred to as NNRGA throughout this chapter. In the NNRGA method, at each iteration of the RGA, a neural network classifier is applied to the individuals of the current population created by the RGA (possible solutions), and any profile that does not “look like” a breast profile is disregarded. A smooth profile assumption is not used in the classifier. Instead, realistic assumptions about a breast profile are used.

Using RGAs has a high computational cost but this can be minimized using parallel programming. Parallel programming is a natural choice for RGA optimization because the calculation of the cost function of each individual of the population is independent from the rest.

The chapter is organized as follows. The mathematical formulation of the problem is described in Sect. 5.3 and the NNRGA algorithm is introduced in Sect. 5.4.

5.3 Mathematical Formulation

Consider an inaccessible investigation domain containing a dielectric scatterer of arbitrary bounded cross section (Fig. 5.2) and modeled by the complex permittivity ε(x, y). The location of the boundary of the scatterer (breast) is assumed to be known using skin-sensing methods [34]. The region under investigation (D _I) is illuminated by a set of incident TM waves characterized by z-directed electric fields, $E_{\mathrm{inc}}^{v}(r) = E_{\mathrm{inc}}^{v}(x,y)\hat{z}$ , v = l, …, n _t where n _t is the number of the transmitters. The scattered fields $E_{\mathrm{scatt}}^{m}(x,y)\hat{z}$ , (x, y)∉D _Iarising from multiple-scattering interactions between incident waves and the unknown object are collected in m = 1, …, n _r measurement points located in an area called the observation domain D _O, external to the investigation domain D _I. The background medium is assumed to be homogeneous, nonmagnetic, and filled by a matching media with relative permittivity of 23.4 and conductivity of 1.13 S.m⁻¹ [5].

Fig. 5.2

Problem geometry

The goal of the imaging process is to retrieve the distribution of the complex permittivity ε(x, y) starting from the knowledge of the scattering data ( $E_{\mathrm{scatt}}^{m}(x_{m},y_{m})$ , m = 1, …, n _r and $(x_{m},y_{m}) \in D_{O}$ ), by modeling the nonlinear electromagnetic interactions using Maxwell’s equations. FDTD [35–38] is used to discretize and numerically solve Maxwell’s equations. After discretization, the problem unknowns are represented through a linear combination of rectangular basis functions R _n(x, y), n = 1, …, N as follows:

$\displaystyle{ \epsilon (x,y) =\sum _{ n=1}^{N}\epsilon _{ n}R_{n}(x,y),\qquad (x,y) \in D_{I}, }$

(5.1)

where ε _nrepresents the dielectric properties of the nth basis function and is assumed constant over its area and N is the number of basis functions. The selection of the parameters in our simulations is so that each basis function represents an unknown in the search space (more explanation is given in Sect. 5.4.4). The inverse problem is then recast as the global minimization of a cost function (fitness function) which minimizes the error between the simulated and measured scattered fields by searching for the optimum values of ε _n. The definition of the cost function in the NNRGA method is discussed in Sect. 5.4.2. Hypothetical measured data are produced by running a method-of-moment code to avoid “the inverse crime”.

5.3.1 Numerical Phantom

Numerical breast phantoms provided in the UWCEM Numerical Breast Phantom Repository [19] are used to test the NNRGA method. The breast phantoms are derived from a series of T1-weighted MRIs of patients in a prone position. Each phantom is comprised of a 3D grid of cubic voxels, where each voxel is 0. 5 × 0. 5 × 0. 5 mm. Two-dimensional cross sections on the coronal plane are extracted for testing the NNRGA method. The dimension of voxels in the inversion mesh is 4 × 4 × 4 mm. In Sect. 5.4.4, it will be explained that the FDTD mesh cells are chosen to have the dimension of 4 × 4 mm too. If the inversion algorithm works perfectly, the obtained images would be identical to the 2-dimensional MR images subsampled by a factor of 8 in each dimension.

Table 5.1

Range of the values of permittivity and conductivity for different categories of breast tissues at 1 GHz [18]

Tissue category	Minimum of ε _r	Maximum of ε _r	Minimum of σ[1∕(ohm.m)]	Maximum of σ[1∕(ohm.m)]
Fibroconnective/Glandular group 1	54.4216	68.9448	1.0067	1.5138
Fibroconnective/Glandular group 2	49.1244	54.4216	0.8984	1.0067
Fibroconnective/Glandular group 3	37.2283	49.1244	0.5071	0.8984
Transitional	7.5112	37.2283	0.0960	37.2283
Fatty group 1	4.6974	7.5112	0.0572	0.0960
Fatty group 2	3.9423	4.6974	0.0098	0.0572
Fatty group 3	2.4004	3.9423	0.0054	0.0098

Breast tissue is categorized into seven types. The range of the dielectric properties of these types is defined in Table 5.1. The dielectric properties of each voxel in the repository are determined by its type and water content using the single-pole Debye model [39]. The following set of equations express this relationship [40]:

$\displaystyle{ \epsilon _{s} = P\epsilon _{s\mathrm{u}} +\epsilon _{s\mathrm{l}} - P\epsilon _{s\mathrm{l}}, }$

(5.2)

where P is the water content percentage, ε _sis the dielectric constants at zero (static) frequency, and ε _sl and ε _su are the dielectric constants at zero frequency for the lower and upper bounds of the corresponding group, respectively.

$\displaystyle{ \epsilon _{\infty } = P\epsilon _{\infty \mathrm{u}} +\epsilon _{\infty \mathrm{l}} - P\epsilon _{\infty \mathrm{l}}, }$

(5.3)

where ε _∞is the dielectric constant at infinite frequency and ε _∞l and ε _∞u are the permittivities at infinite frequency for the lower and upper bounds of the corresponding group, respectively.

$\displaystyle{ \sigma _{s} = P\sigma _{\mathrm{u}} +\sigma _{\mathrm{l}} - P\sigma _{\mathrm{l}} }$

(5.4)

where σ _sis the conductivity at zero frequency and σ _l and σ _u are the conductivities at the lower and upper bounds of the corresponding group, respectively. The Debye approximation is given by

$\displaystyle{ \epsilon _{r} =\epsilon _{\infty } + \frac{\epsilon _{s} -\epsilon _{\infty }} {1 + j\omega \tau } - j\frac{\sigma _{s}} {\omega \epsilon _{0}}, }$

(5.5)

where ε ₀ is the free space permittivity, ε _ris the complex permittivity at the angular frequency ω, and τ is the relaxation time constant.

5.4 The NNRGA Method

Figure 5.3 shows the block diagram of the NNRGA method. The RGA minimizes the error between the simulated and measured data. At each iteration of the RGA, all the individual solutions of that generation enter a neural network classifier. The neural network classifier determines whether each solution “looks like” a breast profile. If the solution looks like a breast profile, the error between the recorded and simulated data will be calculated. If it does not look like a breast profile, a large number is assigned to its fitness value to reduce its chance of being reproduced in the next generation of the GA.

The RGA is described in Sect. 5.4.2. In Sect. 5.4.3, feature extraction and the neural network classification are explained. In this section, the criterion of “looking like a breast profile” will be clarified. Finally, Sect. 5.4.4 explains how the parameters of the NNRGA method are selected.

Fig. 5.3

Block diagram of the NNRGA method

In the NNRGA method, the main variables in the optimization process are the relative permittivities of the voxels. The conductivity values depend on the relative permittivity values through the water content P. Therefore, instead of optimizing for both relative permittivity and conductivity, the NNRGA only optimizes for the relative permittivity values. This is explained in the following section.

5.4.1 Variable Reduction

The values of relative permittivity and conductivity in the breast tissue are correlated through the water content variable. Imagine that at each iteration of the RGA, the value of ε is known. Then, based on Table 5.1, the parameters ε _s, ε _∞, σ _s, and σ _∞can be obtained. The value of P can then be obtained by solving Eqs. (5.2)–(5.5) for P:

$\displaystyle{ P = \frac{\epsilon _{s\mathrm{l}} -\epsilon _{\infty \mathrm{l}} -\epsilon (1 +\omega ^{2}\tau ^{2}) + (1 +\omega ^{2}\tau ^{2})\epsilon _{\infty \mathrm{l}}} {\epsilon _{\infty \mathrm{u}} -\epsilon _{\infty \mathrm{l}} - (1 +\omega ^{2}\tau ^{2})\epsilon _{\infty \mathrm{u}} + (1 +\omega ^{2}\tau ^{2})\epsilon _{\infty \mathrm{l}} -\epsilon _{s\mathrm{u}} +\epsilon _{s\mathrm{l}}}. }$

(5.6)

Once the value of P is found, Eqs. (5.2)–(5.5) can be solved again to find the value of σ. Therefore, the values of ε and σ are not independent. Once ε is known, the value of σ is forced by Eqs. (5.2) through (5.5).

Therefore, relative permittivity can be considered as the primary variable for optimization. This approach reduces optimization variables by half and increases the convergence speed.

5.4.2 Genetic Algorithm

Real coding is utilized in our implementation of the genetic algorithm. Real-coded GA is preferable to binary-coded GA for continuous search spaces [27]. In the real-coded GA, each gene is a random number picked from a uniform distribution: C _min ≤ c(k) ≤ C _max, 1 ≤ k ≤ N where C _min and C _max are the minimum and maximum possible values of the relative permittivity of the breast tissue at the irradiation frequency of 1 GHz (Table 5.1) and N is the number of individuals in each generation. In this chapter the cost function is then calculated for each individual in the population. The cost function is defined as

$\displaystyle{ \acute{c_{i}} = \left \{\begin{array}{ll} F(i,j) = A &\mbox{ if $T \leq 0.5$ } \\ F(i,j) =\sum _{ l=1}^{n_{\mathrm{t}}}\sum _{m=1}^{n_{\mathrm{r}}}(E_{r}(l,m) - E_{s}(l,m))^{2} & \text{otherwise }\\ \end{array} \right.\!\!\!\!, }$

(5.7)

where F(i, j), i = 1, …, N, j = 1, …, J is the fitness value of the ith individual in the jth generation, J is the number of generations, and T is the output of the neural network classifier. Details of how T is calculated are given in Sect. 5.4.3. In short, T ≤ 0. 5 means that the neural network classifier has identified the individual solution as one that cannot be a breast profile. A is a number which satisfies $$$A >>\sum _{ l=1}^{n_{\mathrm{t}}}\sum _{m=1}^{n_{\mathrm{r}}}(E_{r}(l,m) – E_{s}(l,m))^{2};\forall l,m$$ ” src=”https://radiologykey.com/wp-content/uploads/2020/04/A305155_1_En_5_Chapter_IEq5.gif”>; n t and n r are the number of transmitters and receivers, respectively. The value of A is chosen to be much greater than <IMG alt=$ . This reduces the selection chance of an individual solution that does not look like a breast profile in the next generation and therefore removes the ill-posed answers and limits the search space.

While the individual with the minimum cost value is saved (elitism), the rest of the population undergoes a roulette wheel selection where the probability of the individual selection (i, j) is $\frac{f(i,j)} {\sum _{i=1}^{N}f(i,j)}$ . Then, arithmetic crossover is applied as explained in Chap. 4.

5.4.3 Neural Network Classifier

At each iteration of the genetic algorithm, many new individuals in the search space are created. Many of these randomly created new individuals do not possess the characteristics of a breast profile and therefore cannot be the correct answer of the inverse scattering problem in the breast imaging application. A neural network classifier is used to distinguish potential breast-like profiles and remove the profiles that cannot be a profile of the dielectric properties of a breast (we call them non-breast profiles in this chapter). Removing non-breast profiles regularizes the algorithm because non-breast profiles, if not removed, can produce many local minima in the cost function.

The neural network is used as the classifier in the NNRGA method. The job of this classifier is to determine whether each solution in one generation of the RGA looks like a breast profile or not. In other words, the neural network classifier has to quantify the inherently qualitative concept of “looking like a breast profile.” Classification methods use some features of the input data to determine the class of the input. The most important factor in a successful classification is the definition of the features. If the features show a great contrast between the different classes, the classifier is normally able to classify the inputs correctly. The need for a classifier arises when there is no single feature that can divide the inputs into distinct classes. In our case, we could not find a single feature that is always different among the breast and random profiles. Therefore, we need a classifier along with multiple features to be able to differentiate between the random and breast classes.

We used a two-layer neural network, with a tan-sigmoid transfer function in the hidden layer and a linear transfer function in the output layer which uses 12 features. A two-layer neural network is typical for a network of 13 features. The network uses the Levenberg–Marquardt algorithm [41, 42] for training. The Levenberg–Marquardt algorithm is also widely used for training the neural networks.

Two hundred breast profiles from the UWCEM Numerical Breast Phantom Repository [19] and 200 non-breast (random) profiles were used to train the network. The 200 breast profiles that are used for training the neural network are two-dimensional cross sections of nine numerical breast phantoms from all different categories of breast tissue including mostly fatty, scattered fibroglandular, heterogeneously dense, and very dense. This ensures that the classification will work well on different breast types. In addition, the flexibility of neural network classification allows the training to be improved if more breast samples are added to the repository.

Figure 5.4 shows two-dimensional cross sections of four different breast types. The 12 features used for classification are:

Fig. 5.4

Relative permittivity of four sample cross sections from different breast types used for testing the NNRGA method. Skin layer and matching media are not shown to allow higher contrast for better demonstration. (a) A mostly fatty sample, (b) a scattered fibroglandular sample, (c) a heterogeneously dense sample, and (d) a very dense sample

Percentage of the tissues in fatty group 1, fatty group 2, fatty group 3, fibroglandular group one, fibroglandular group two, fibroglandular group three, transitional group, and total percentage of the fatty tissue are eight of the features used for classification. The extraction of these features is straightforward. First, each voxel of the imaging domain is categorized into one of the tissue categories based on the data in Table 5.1. Then the percentage of tissues in each category is easily calculated by dividing the number of voxels in that category by the total number of voxels in the breast profile. This normalization is necessary because the size of the profile varies depending on the breast size and location of the cross section.
The number of connected fatty regions and connected fibroglandular regions are the next two features used for classification. To find the number of connected fibroglandular regions, first a binary image is created using the following criteria:

$\displaystyle{ I_{n1}(i,j) = \left \{\begin{array}{ll} 1&\mbox{ if $\epsilon _{g\mathrm{l}} \leq I_{n}(i,j) \leq \epsilon _{g\mathrm{u}}$ } \\ 0&\text{otherwise }\\ \end{array} \right.\!\!\!, }$

(5.8)
where ε _gl = 37. 23 and ε _gu = 68. 94 are the lower and upper bounds of relative permittivity of the fibroglandular tissue (Table 5.1), I _n(i, j) is the value of the relative permittivity in the (i, j) position of the nth individual in the current population, and I _n1(i, j) is its binary version showing whether that voxel is of fibroglandular tissue. In order to find the number of connected fatty regions, first a binary image is created using the following criteria:

$\displaystyle{ I_{n2}(i,j) = \left \{\begin{array}{ll} 1&\mbox{ if $\epsilon _{f\mathrm{l}} \leq I_{n}(i,j) \leq \epsilon _{f\mathrm{u}}$} \\ 0&\text{otherwise }\\ \end{array} \right. }$

(5.9)
where ε _fl and ε _fu are the lower and upper bounds of relative permittivity of fatty tissues (Table 5.1) and I _n2(i, j) indicates whether voxel (i, j) belongs to the fatty category. Once I _n1 and I _n2 are found, the number of connected regions is obtained using the method in [43]. In this method, the pixels with the value of 1 are considered the objects and the pixels with the value of 0 are considered the background. The method uses the 4-connectivity approach. Eight-connectivity means that two pixels are considered connected if they are both equal to 1 and they are neighbors in one of the following directions: north, south, west, east, northwest, northeast, southwest, and southeast.

Only gold members can continue reading. Log In or Register to continue
Share this:
Related posts:

Introduction to Microwave Imaging Parallel Forward Solver Benchmarking Parallel Evolutionary Algorithms Sequential Optimization: Genetic Algorithm Sequential Forward Solver Global Optimization: Differential Evolution, Genetic Algorithms, Particle Swarm, and Hybrid Methods

Stay updated, free articles. Join our Telegram channel