…although nature begins with the cause and ends with the the …although nature begins with the cause and ends with the
experience we must follow the opposite course, namely
…begin with the experience and by means of it
end with the cause.
Leonardo da Vinci
An inverse problem is the flip side of some direct problem. Direct problems treat the transformation of known causes into effects that are determined by some specified model of a natural process. They tend to be future directed and outward looking and are often concerned with forecasting or with determining external effects of internal causes. Direct problems have solutions (causes have effects), and the process of transforming causes into effects is a mathematical function: a given cause determines, via the model, a unique effect. In direct problems the operator that maps causes into effects is typically continuous in natural metrics: close causes have close effects. These features of direct problems make them well posed.
The idea of a well-posed problem has its origins in Jacques Hadamard’s short paper [37] published in 1902. Hadamard held the opinion that an important physical problem must have three attributes:
1.
(Existence) It has a solution.
2.
(Uniqueness) It has only one solution.
3.
(Stability) The solution depends continuously on the data of the problem.
A problem satisfying these three conditions is called well posed. In his 1902 paper, Hadamard called a problem bien posé if it has properties (1) and (2). Again in his 1923 lectures [38], he called a problem “correctly set” if it satisfies (1) and (2). Condition (3) was not named as a specific requirement of a well-posed problem, but his explicit notice of the lack of continuous dependence on boundary data of the solution of Cauchy’s problem for Laplace’s equation led to (3) becoming part of the accepted definition of a well-posed problem.
A problem is ill posed if it lacks these qualities. Hadamard’s suggestion that ill-posed problems are devoid of physical significance (déprourvu de signification physique) was unfortunate, as almost all inverse problems in the physical and biological sciences are ill posed. To be fair, it should be noted that Hadamard was speaking about a specific problem, the Cauchy problem for Laplace’s equation in a strip. On the other hand, Courant [15] insisted more generally that “a mathematical problem cannot be considered as realistically corresponding to physical phenomena unless …” it satisfies condition (3). The problems of existence and uniqueness in inverse problems can often be ameliorated by generalizing the notion of solution and constraining the generalized solution, but the key attribute of stability often is a feature that is inherently absent in inverse problems. This essential lack of stability usually has dire consequences when numerical methods, using measured or uncertain data, are applied to inverse problems.
Inverse problems are as old as science itself. In fact, a reasonable working definition of science is the explanation of natural phenomena by the construction of conceptual models for interpreting imperfect observational representations of “true” natural objects or processes. This definition encompasses the three essential ingredients of mathematical inverse problems: a “true” solution, a model, or operator that transforms this true solution into an imperfect representation that is amenable to observations or measurements. One could say that inverse theory embraces an operating principle that is essentially Platonic: true natural objects exist, but it is only through models and imperfectly perceived images that we experience them. The challenge is to “invert” the model to recover a useful estimate of the true object from the observed image. In this sense, all of inverse theory deals with “imaging.”
A mathematical framework for the study of inverse problems must provide sufficient scope for each of the three elements: true solutions, model, and observations. In this chapter the solution space and the space of observations are both taken to be Hilbert spaces, but not necessarily the same Hilbert space, as one naturally desires more of the solution than one demands from the observations. The model is a transformation or operator that carries a possible solution to an observed effect. We consider only linear inverse problems, so our models are linear operators.
Any practical model suppresses some information. If a model represents every bit of information in the objects themselves (i.e., the model operator is the identity operator), then nothing is gained in conceptual economy. In this case one is in the absurd position of Mein Herr in Lewis Carroll’s Sylvie and Bruno Concluded:
“We actually made a map of the country, on a scale of a mile to the mile!” …“It has never been spread out yet,” said Mein Herr: “the farmers objected; they said it would cover the whole country, and shut out the sunlight! So now we use the country itself, as its own map, and I assure you it does nearly as well.”
Finite linear models lead to linear algebra problems. Idealized limiting versions of finite models typically lead to compact linear operators, that is, limits of finite rank operators. A compact operator may have a nontrivial null-space, a non-closed range, or an unbounded (generalized) inverse. Therefore, these operators, which occur widely in models of linear inverse problems, lack all the virtues of well posedness. In this chapter, we provide a somewhat slanted survey of linear inverse problems, mainly involving compact operators, with special attention to concepts underlying methods for constructing stable approximate solutions.
Before draping these ideas on a mathematical framework, we discuss a half dozen examples of model inverse problems that have played significant roles in the development of the physical sciences.
2 Background
 Our science is from the watching of shadows; shadows; Our science is from the watching of shadows;
Our science is from the watching of shadows; shadows; Our science is from the watching of shadows; Ezra Pound
This brief and incomplete historical survey of physical inverse problems is meant to give some perspective on certain inverse problems closely related to imaging in the broad sense. Our viewpoint involves both the very large scale, treating inverse problems loosely associated with assessing the cosmos, and the human scale, dealing with evaluation of the inaccessible interior of bodies (human or otherwise).
Inverse theory, as a distinct field of inquiry, is a relatively recent development; however, inverse problems are as old as science itself. A desire to know causes of perceived effects is ingrained in the human intellectual makeup. The earliest attempts at explanations, as, for example, in the creation myths of various cultures, were supernatural – grounded in mysticism and mythology. When humankind embarked on a program of rationalization of natural phenomena, inverse problems emerged naturally and inevitably. An early example is Plato’s allegory of the cave (ca. 375 B.C.). In the seventh book of his Republic, Plato describes the situation. A group of people have been imprisoned since their birth in a cave where they are chained in such a manner that allows them to view only a wall at the back of the cave. Outside the cave life goes on, illuminated by a fire blazing in the distance. The captives in the cave must reconstruct this external reality on the basis of shadows cast on the rear wall of the cave. This is the classic inverse imaging problem: real objects are perceived only as two-dimensional images in the form of shadows on the cave wall. This annihilation of a dimension immediately implies that the reconstruction problem has multiple solutions and that solutions are unstable in that highly disparate objects may have virtually identical images.
Aristotle adapted his teacher Plato’s story of the cave to address a scientific inverse problem: the shape of the earth. This shape could not be directly assessed in Aristotle’s time, so he suggested an indirect approach (see Book II of On the Heavens.):
As it is, the shapes which the moon itself each month shows are of every kind – straight, gibbous, and concave – but in eclipses the outline is always curved; and since it is the interposition of the earth that makes the eclipse, the form of the line will be caused by the form of the earth’s surface, which is therefore spherical.
Aristotle’s reasoning provided an indirect argument for the sphericity of the earth based on the shapes of shadows cast on the moon.
Inverse imaging has been a technical challenge for centuries. The difficulties that early investigators encountered were vividly captured by Albrecht Dürer’s woodcut Man Drawing a Lute (1525). We can see the doubts and angst brought on by the inverse imaging problem etched on the face of the crouching technician (Fig. 1).


Fig. 1
A renaissance inverse problem
The character on the left, standing bolt upright in a confident attitude, has the comparatively easy direct problem. He has complete knowledge of the object, and he knows exactly how the projection model will produce the image. On the other hand, the crouching man on the right, with the furrowed brow, faces the more difficult inverse problem of assessing whether the image captures the essential features of the object. Dürer’s woodcut is a striking representation of the comparative difficulties of direct and inverse assessment.
Modern imaging science has its roots in Galileo Galilei’s lunar observations carried out during the winter of 1609. Prior to Galileo’s study, the moon was thought to belong to the realm of the Pythagorean fifth essence, consisting of perfectly uniform material in perfect spherical form. Galileo’s eyes, empowered by his improved telescope, the earliest scientific imaging device, showed him otherwise [21]:
…we certainly see the surface of the Moon to be not smooth, even, and perfectly spherical, as the great crowd of philosophers has believed about this and other heavenly bodies, but, on the contrary, to be uneven, rough, and crowded with depressions and bulges. And it is like the Earth itself, which is marked here and there with chains of mountains and depth of valleys.
But Galileo was not satisfied with qualitative evidence. He famously stated that the book of nature is written in the language of mathematics, and he used mathematics, in the form of the Pythagorean theorem, along with some shrewd estimates, to assess indirectly the heights of lunar mountains. The process of indirect assessment is a hallmark of inverse problems in the natural sciences. (See [2] for an account of inverse problems of indirect assessment.)
Nonuniqueness is a feature of many inverse problems that was slow to gain acceptance. An early instance of this phenomenon in a physical inverse problem occurred in the kinematic studies of ballistics carried out by Niccolò Tartaglia in the sixteenth century. Tartaglia claimed to be the inventor of the gunner’s square, a device for measuring the angle of inclination of a cannon. Using his square Tartaglia carried out ranging trials and published some of the earliest firing tables. He studied not only the direct problem of finding ranges for a given firing angle but also the inverse problem of determining the firing angle that results in a given range. Although Tartaglia’s treatment was conceptually flawed and lacked rigor, his work contains glimmers of a number of basic principles of mathematical analysis that took several centuries to mature [32]. Tartaglia was particularly struck by nonuniqueness of solutions of the inverse problem. As he put it proudly in the dedication of his book Nova Scientia (Venice, 1537):
I knew that a cannon could strike in the same place with two different elevations or aimings, I found a way of bringing about this event, a thing not heard of and not thought by any other, ancient or modern.
With this boast Tartaglia was one of the first to call attention to this common feature of nonuniqueness in inverse problems.
Tartaglia found that for a given fixed charge, each range (other than the maximum range) is achieved by two distinct aimings placed symmetrically above and below the 45∘ inclination. A century and a half later, Edmond Halley [39] took up the more general problem of allowing both the charge and the firing angle to vary while firing on a fixed target situated on an inclined plane. In this case the inverse problem of determining charge-angle pairs that result in a strike on the target has infinitely many solutions. (Of course, Halley did not address air resistance; his results are extended to the case of first-order resistance in [33].) Halley restored uniqueness to the inverse aiming problem by restricting consideration to the solution which minimizes what we would now call the kinetic energy of the emergent cannon ball. The idea of producing uniqueness by seeking the solution that minimizes a quadratic functional would in due course become a key feature of inverse theory.
The model for a modern scientific society was laid out in Francis Bacon’s utopian novel The New Atlantis (1626). Bacon describes a voyage to the mythical land of Bensalem, which was inhabited by wise men inclined to inverse thinking. Solomon’s House, a research institute in Bensalem, was dedicated to the “knowledge of causes, and secret motions of things; and the enlarging of the bounds of human empire, to the effecting of all things possible” (my italics). The Royal Society of London, founded in 1660 and modeled on Baconian principles, was similarly dedicated. The first great triumph (due largely to Halley’s efforts) of the Royal Society was the publication of Newton’s magisterial Principia Mathematica (1687). In the Principia, Newton’s laws relating force, mass, and acceleration, combined with his inverse square law of gravity, were marshaled to solve the direct problem of two-body dynamics, confirming the curious form of Kepler’s planetary orbits: an inverse square centrally directed force leads to an orbit, which is a conic section. But Newton was not satisfied with this. He also treated the inverse problem of determining what gravitational law (cause) can give rise to a given geometrical orbit (effect).
In the history of science literature, the problem of determining the orbit, given the law of attraction, is sometimes called the inverse problem; this practice inverts the terminology currently common in the scientific community. The reverse terminology in the history community is evidently a consequence of the fact that Newton took up the determination of force law first and then treated the orbit determination problem. Indeed, Newton treated the inverse problem of orbits before he took up the direct problem. After all, his primary goal was to discover the laws of nature, the causes, rather than the effects. As Newton put it in the preface to the first edition of his Principia: “ …the whole burden of philosophy seems to consist of this – from the phenomena of motions to investigate the forces of nature, and then from these forces to demonstrate the other phenomena.”
In 1846, mathematical inverse theory produced a spectacular scientific triumph – the discovery of another world. The seeds of the discovery lay in the observed irregularities in the orbit of Uranus, the most distant of the planets known at the time. The orbit of Uranus did not fit with predictions based on Newton’s theories of gravity and motion. In particular an orbit calculated to fit contemporary observations did not fit observations made in the previous century, and an orbit that fit to the older sightings did not match the contemporary data. This suggested two possibilities: either Newton’s theory had to be modified at great distances or perhaps the anomalies in the orbit of Uranus were the effect of an as yet undiscovered planet (the cause) operating on Uranus via Newton’s laws.
During the summer vacation of 1841, John Couch Adams, an undergraduate of St. John’s College, Cambridge, was intrigued by the second possibility. He recorded this diary entry:
1841, July 3. Formed a design in the beginning of the week, of investigating, as soon as possible after taking my degree, the irregularities in the motion of Uranus, which are yet unaccounted for; in order to find whether they may be attributed to the action of an undiscovered planet beyond it; and if possible thence to determine the elements of its orbit, etc. approximately, which would probably lead to its discovery.
Adams solved the inverse problem of determining the characteristics of the orbit of the undiscovered planet, now known as Neptune, that perturbs Uranus. However, a sequence of lamentable missteps, involving his own timidity, bureaucratic inertia, and other human factors, resulted in the honor of “discovering” the new planet on the basis of mathematics going to Urbain Le Verrier of France, who solved the inverse problem independently of Adams. This of course led to disappointment in England over the botched opportunity to claim the discovery and to a good deal of hauteur in France over the perceived attempt by the English to grab credit deserved by a Frenchman. The fascinating story of the unseemly squabble is well told in [36]. See also [63] for a recent update in which old wounds are reopened.
Newton’s discussion of inverse orbit problems in his Principia, and vague doubts about the form of the gravitational force law raised prior to the discovery of Neptune, may have inspired other inverse problems. An early interesting “toy” inverse problem in this vein was published by Ferdinand Joachimstahl in 1861 [47]. The problem Joachimstahl posed, and solved by an Abel transform, was to determine the law of gravitational attraction if the total force at any distance from a line of known mass density is given.
Johann Radon laid the foundation of mathematical imaging science, without knowing it, in his 1917 memoir [61]. (An English translation of Radon’s paper may be found in [17].) Radon was concerned with the purely mathematical problem of determining a real-valued function of two variables from knowledge of the values of its line integrals over all lines intersecting its domain. Although Radon evidently had no application in mind, his treatment was to become, after its rediscovery a half century later, the basis for the mathematics of computed tomography. (See [14] for more on the history of computed tomography.) Essentially the same result was obtained independently by Viktor Ambartsumian [1] who was interested in a specific inverse problem in astronomy. Proper motions of stars are difficult to determine, but radial velocities (relative to the earth) are obtainable from chromatic Doppler shift measurements. Ambartsumian used a mathematical model essentially equivalent to that of Radon to deduce the true three-dimensional distribution of stellar velocities from the distribution of the radial velocities.
In the mid-1950s of the last century, Allan Cormack, a young physics lecturer at the University of Cape Town, who was moonlighting in the radiology department of Groote Schuur Hospital, had a bright idea. In Cormack’s words:
It occurred to me that in order to improve treatment planning one had to know the distribution of the attenuation coefficient of tissues in the body, and that this distribution had to be found by measurements made external to the body. It soon occurred to me that this information would be useful for diagnostic purposes and would constitute a tomogram or series of tomograms, though I did not learn the word “tomogram” for many years.
This was the birth of the mathematical theory of medical imaging. Cormack would not learn of Radon’s work for another two decades, but he developed the basic results for radially symmetric attenuation coefficient distributions and tested the theory with good results on a simple manufactured specimen in the form of a cylinder of aluminum encased in an annular prism of wood. The reconstructed piecewise constant attenuation function matched that of the known specimen well enough to show the promise of this revolutionary new imaging technology.
In the 1990s, inverse thinking and indirect assessment led to another spectacular advance in astronomy: the discovery of extrasolar planets. Philosophers had speculated on the reality of planets linked to the stars at least since classical Greek times, and few in modern times doubted the existence of extrasolar planets. But convincing evidence of their existence had to await the development of sufficiently sensitive telescope-mounted spectrometers and the application of simple inverse theory. The indirect evidence of extrasolar planets consisted of spectral shift data extracted from optical observations of a star.
In a single star–planet system, determining the variable radial velocity (relative to the earth) of a star wobbling under the gravitational influence of an orbiting planet of known mass and orbital radius is a simple direct problem – just equate the gravitational acceleration of the planet to its centripetal acceleration. (Consider only the simple case in which the planet, star, and earth are coplanar and the orbit is circular; an orbit oblique to the line of sight from earth introduces an additional unknown quantity. As a consequence of this obliquity, the relative mass estimated from the inverse problem is actually a lower bound for this quantity.) Using Doppler shift data, a simple inverse problem model may be developed for determining approximations to the relative planetary mass and orbital radius. The solution of the inverse problem enabled astronomers to announce in 1995 the existence of the first confirmed extrasolar planet orbiting the star 51Pegasi. The millennia-old question of the existence of extrasolar worlds finally had a convincing positive answer.
We bring this historical survey of inverse problems up to the present day with the greatest challenge in contemporary cosmology: the search for dark matter. Such matter, being “dark,” is by definition inaccessible to direct measurement. But recently an imaging model on the largest scale in the history of science has come to be used in attempts to assay this dark matter. The process of gravitational lensing, which is based on Einstein’s theory of curved space-time, presents the possibility of inverting the imaging model to estimate a dark mass (the gravitational lens) that intervenes between the observer on earth and an immensely distant light source. The dark mass warps space in its vicinity resulting, under appropriate conditions, in focusing onto the earth light rays that in flat space would not intersect the earth. In an extreme case in which the light source (e.g., a galaxy), the intervening gravitational lens (dark matter), and the collected image are collinear, this results in a phenomenon called an Einstein ring (first observed in 1979; see [22]). If the distances from earth to the lens and from the lens to source can be estimated, then the solution of an inverse problem gives an estimate of the dark mass (see [56]).
3 Mathematical Modeling and Analysis
 …we have to remember that what we observe is not nature in itself itself …we have to remember that what we observe is not nature in itself
…we have to remember that what we observe is not nature in itself itself …we have to remember that what we observe is not nature in itself but nature exposed to our method of questioning.
Werner Heisenberg
A Platonic Inverse Problem
Plato’s discussion of captives struggling to discern the real cause of shadows cast on the back wall of a cave is a primeval exemplar of inverse imaging problems. Here we present a toy imaging problem inspired by Plato’s allegory. While the problem is very elementary, it usefully illustrates some important aspects of imaging problems and inverse problems in general.
Imagine a two-dimensional convex object in the xy-plane, which is bounded by the positive coordinate axes, and the graph of a function y = f(x), 0 ≤ x ≤ 1 that is positive on [0, 1), strictly decreasing and concave-down, and satisfies f(1) = 0 = f ′ (0). The object is illuminated by parallel light rays from the left that form angles θ with the negative ray of the horizontal axis, as illustrated in Fig. 2.
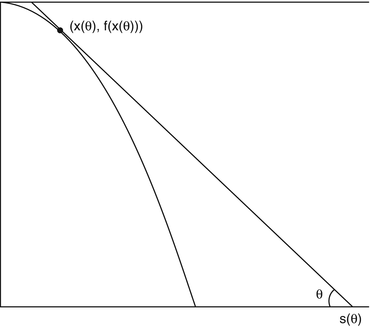

Fig. 2
A model shadow problem
The goal is to reconstruct the shape of the object from observations of the extent s(θ) of the shadow cast by the object. This is accomplished by fashioning a parameterization (x(θ), f(x(θ))) of the boundary curve of the object. As a further simplification we assume that f ′ (1) = −1. These assumptions guarantee that for each s > 1 there is a unique point (t, f(t)) on the graph of f at which the tangent line intersects the x-axis at s. What is required to see this is the existence of a unique t ∈ (0, 1) such that the tangent line to the graph at the point (t, f(t)) intersects the x-axis at s. That is,
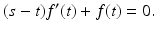 For each fixed s > 1, the expression on the left is strictly decreasing for t ∈ (0, 1), positive at t = 0 and negative at t = 1, so the existence of a unique such t = x(θ) is assured. At the point of tangency,
For each fixed s > 1, the expression on the left is strictly decreasing for t ∈ (0, 1), positive at t = 0 and negative at t = 1, so the existence of a unique such t = x(θ) is assured. At the point of tangency,
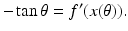 Also,
Also,
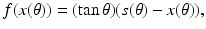 and hence determining x(θ) also gives (x(θ), f(x(θ))), which solves the inverse imaging problem. Combining these results we have
and hence determining x(θ) also gives (x(θ), f(x(θ))), which solves the inverse imaging problem. Combining these results we have
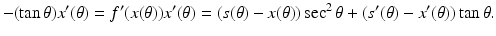 A bit of simplification yields
A bit of simplification yields
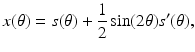
which explicitly solves the inverse problem of determining the shape (x(θ), f(x(θ))) from knowledge of the extent of the shadows s(θ).
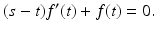
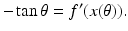
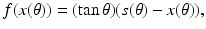
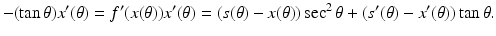
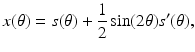
(1)
The explicit formula (1) would seem to completely solve the inverse problem. In a theoretical sense this is certainly true. However, the formulation (1) shelters a subversive factor (the derivative) that should alert us to potential challenges involved in the practical solution of the inverse problem. Observations are always subject to measurement errors. The differentiation process, even if performed exactly, may amplify these errors as differentiation is a notoriously unstable process. For example, if a shadow function s(θ) is perturbed by low-amplitude high-frequency noise of the form 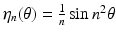 giving observed data
giving observed data
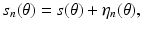 then the corresponding shape abscissas provided by (1) satisfy
then the corresponding shape abscissas provided by (1) satisfy
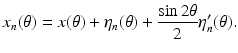 But η n converges uniformly to 0 as n → ∞, while
But η n converges uniformly to 0 as n → ∞, while 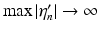 , giving a convincing illustration of the instability of the solution of the inverse problem provided by (1). For more examples of model inverse problems with explicit solutions that involve differentiation, see [71].
, giving a convincing illustration of the instability of the solution of the inverse problem provided by (1). For more examples of model inverse problems with explicit solutions that involve differentiation, see [71].
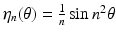 giving observed data
giving observed data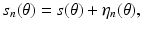
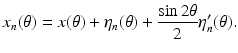
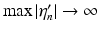 , giving a convincing illustration of the instability of the solution of the inverse problem provided by (1). For more examples of model inverse problems with explicit solutions that involve differentiation, see [71].
, giving a convincing illustration of the instability of the solution of the inverse problem provided by (1). For more examples of model inverse problems with explicit solutions that involve differentiation, see [71].It is instructive to view the inverse problem from another perspective. Note that by (1), s(θ) is the solution of the linear differential equation
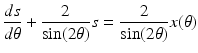 satisfying s(π∕4) = 1. This differential equation may be solved by elementary means yielding
satisfying s(π∕4) = 1. This differential equation may be solved by elementary means yielding
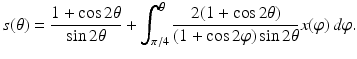
In this formulation, the “hidden” solution 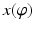 of the inverse problem is seen to be transformed by a linear integral operator into observations of the shadows s(θ). The goal now is to uncover
of the inverse problem is seen to be transformed by a linear integral operator into observations of the shadows s(θ). The goal now is to uncover 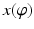 from (2) using knowledge of s(θ), that is, one must solve an integral equation.
from (2) using knowledge of s(θ), that is, one must solve an integral equation.
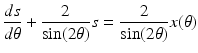
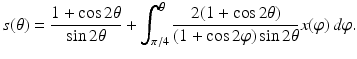
(2)
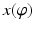 of the inverse problem is seen to be transformed by a linear integral operator into observations of the shadows s(θ). The goal now is to uncover
of the inverse problem is seen to be transformed by a linear integral operator into observations of the shadows s(θ). The goal now is to uncover 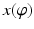 from (2) using knowledge of s(θ), that is, one must solve an integral equation.
from (2) using knowledge of s(θ), that is, one must solve an integral equation.The solution of the integral formulation (2) suffers from the same instability as the explicit solution (1). Indeed, one may write (2) as
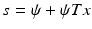
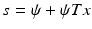
where 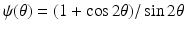 and
and
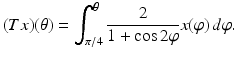 If we let
If we let 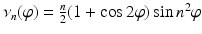 and set
and set
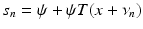 then one finds that s n → s uniformly, while max | ν n | → ∞. That is, arbitrarily small perturbations in the data s may correspond to arbitrarily large deviations in the solution x. This story has a moral: instability is intrinsic to the inverse problem itself and not a manifestation of a particular representation of the solution.
then one finds that s n → s uniformly, while max | ν n | → ∞. That is, arbitrarily small perturbations in the data s may correspond to arbitrarily large deviations in the solution x. This story has a moral: instability is intrinsic to the inverse problem itself and not a manifestation of a particular representation of the solution.
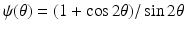 and
and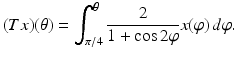
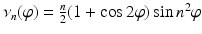 and set
and set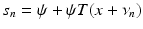
Cormack’s Inverse Problem
As noted in the previous section, the earliest tomographic test problem explicitly motivated by medical imaging was Cormack’s experiment [12] with a fabricated sample having a simple radially symmetric absorption coefficient. The absorption coefficient is a scalar field whose support may be assumed to be contained within the body to be imaged. This coefficient f supplies a measure of the attenuation rate of radiation as it passes through a given body point and is characterized by Bouguer’s law
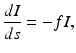 where I is the intensity of the radiation and s is arclength. The integral of f along a line L intersecting the body then satisfies
where I is the intensity of the radiation and s is arclength. The integral of f along a line L intersecting the body then satisfies
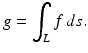 Here g = ln(I 0∕I e ), where I 0 is the incident intensity, and I e the emergent intensity, of the beam. The observable quantity g is then a measure of the total attenuation effect that the body has on the beam traversing the line L.
Here g = ln(I 0∕I e ), where I 0 is the incident intensity, and I e the emergent intensity, of the beam. The observable quantity g is then a measure of the total attenuation effect that the body has on the beam traversing the line L.
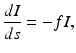
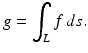
To be more specific, for a given t ∈ R and a given unit vector 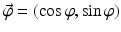 , let
, let 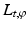 represent the line
represent the line
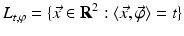 where
where 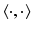 is the Euclidean inner product. We will denote the integral of f over
is the Euclidean inner product. We will denote the integral of f over 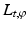 by
by
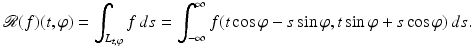 If f is radial, that is, independent of
If f is radial, that is, independent of 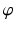 , then
, then
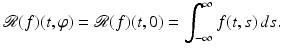
Furthermore, if f vanishes exterior to the disk of radius R, then on setting 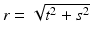 and f(r) = f(t, s), one finds
and f(r) = f(t, s), one finds
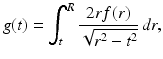
where 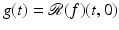 . The mapping defined by (4), which for a given line
. The mapping defined by (4), which for a given line 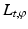 transforms the radial attenuation coefficient into the function g, is an Abel transform of f. It represents, as a direct problem, Cormack’s early experiment with a radially symmetric test body. Determining the distribution of the attenuation coefficient requires solving the inverse problem. The Abel transform may be formally inverted by elementary means to furnish a solution of the inverse problem of determining the attenuation coefficient f from knowledge of the loss data g. Indeed, by (4) and a reversal of order of integration,
transforms the radial attenuation coefficient into the function g, is an Abel transform of f. It represents, as a direct problem, Cormack’s early experiment with a radially symmetric test body. Determining the distribution of the attenuation coefficient requires solving the inverse problem. The Abel transform may be formally inverted by elementary means to furnish a solution of the inverse problem of determining the attenuation coefficient f from knowledge of the loss data g. Indeed, by (4) and a reversal of order of integration,
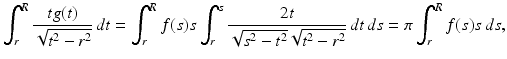 since
since
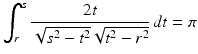 (change the variable of integration to
(change the variable of integration to 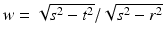 ). However,
). However,
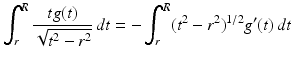 and hence on differentiating, we have
and hence on differentiating, we have
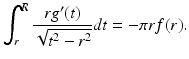 Therefore,
Therefore,
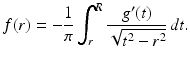 The derivative lurking within this inversion formula is again a harbinger of instability in the solution of the inverse problem.
The derivative lurking within this inversion formula is again a harbinger of instability in the solution of the inverse problem.
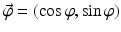 , let
, let 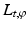 represent the line
represent the line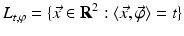
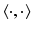 is the Euclidean inner product. We will denote the integral of f over
is the Euclidean inner product. We will denote the integral of f over 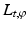 by
by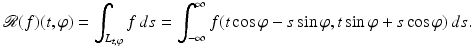
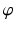 , then
, then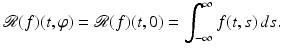
(3)
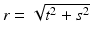 and f(r) = f(t, s), one finds
and f(r) = f(t, s), one finds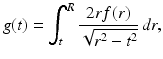
(4)
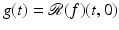 . The mapping defined by (4), which for a given line
. The mapping defined by (4), which for a given line 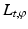 transforms the radial attenuation coefficient into the function g, is an Abel transform of f. It represents, as a direct problem, Cormack’s early experiment with a radially symmetric test body. Determining the distribution of the attenuation coefficient requires solving the inverse problem. The Abel transform may be formally inverted by elementary means to furnish a solution of the inverse problem of determining the attenuation coefficient f from knowledge of the loss data g. Indeed, by (4) and a reversal of order of integration,
transforms the radial attenuation coefficient into the function g, is an Abel transform of f. It represents, as a direct problem, Cormack’s early experiment with a radially symmetric test body. Determining the distribution of the attenuation coefficient requires solving the inverse problem. The Abel transform may be formally inverted by elementary means to furnish a solution of the inverse problem of determining the attenuation coefficient f from knowledge of the loss data g. Indeed, by (4) and a reversal of order of integration,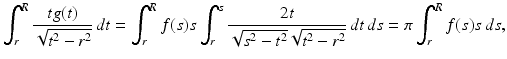
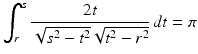
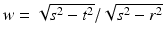 ). However,
). However,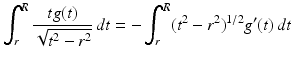
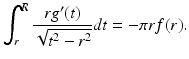
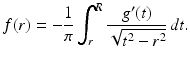
Forward and Reverse Diffusion
Imagine a bar, identified with the interval [0, π] of the x-axis, the lateral surface of which is thermally insulated while its ends are kept always at temperature zero. The diffusion of heat in the bar is governed by the one-dimensional heat equation
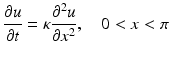 where u(x, t) is the temperature at position x and time t and κ is the thermal diffusivity. If the initial temperature distribution in the bar is a function f(x), then the boundary and initial conditions associated with this model are
where u(x, t) is the temperature at position x and time t and κ is the thermal diffusivity. If the initial temperature distribution in the bar is a function f(x), then the boundary and initial conditions associated with this model are
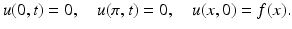 In the forward diffusion problem, the goal is to find, for a given future time T > 0, the temperature distribution g(x) = u(x, T). Formal separation of variable techniques leads to a solution of the form
In the forward diffusion problem, the goal is to find, for a given future time T > 0, the temperature distribution g(x) = u(x, T). Formal separation of variable techniques leads to a solution of the form
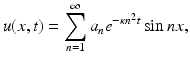 where a n are the Fourier coefficients of the initial temperature distribution
where a n are the Fourier coefficients of the initial temperature distribution
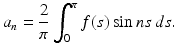 The future temperature distribution is then seen to be, after some rearranging,
The future temperature distribution is then seen to be, after some rearranging,
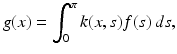 where
where
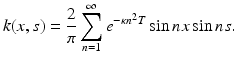 A high degree of smoothing is a notable feature of the forward diffusion process. Specifically, the factors
A high degree of smoothing is a notable feature of the forward diffusion process. Specifically, the factors 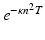 in the transformation have the effect of severely damping high-frequency components in the initial temperature distribution f.
in the transformation have the effect of severely damping high-frequency components in the initial temperature distribution f.
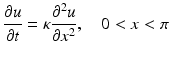
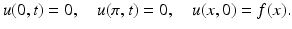
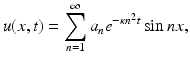
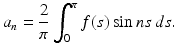
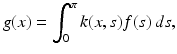
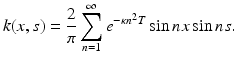
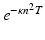 in the transformation have the effect of severely damping high-frequency components in the initial temperature distribution f.
in the transformation have the effect of severely damping high-frequency components in the initial temperature distribution f.A corresponding reverse diffusion process is immediately suggested, namely, the retrodiction of the initial temperature distribution f, from knowledge of the later temperature distribution g. In this inverse problem, one finds that
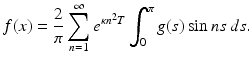
The contrast with the forward problem is striking: now high-frequency components in g are amplified by the huge factors 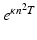 . Also note that the inverse problem is soluble only for a restricted class of functions g – those for which the series (5) converges in L 2[0, π]. As will be seen in the next section, the reverse diffusion process is a useful metaphor in the discussion of deblurring.
. Also note that the inverse problem is soluble only for a restricted class of functions g – those for which the series (5) converges in L 2[0, π]. As will be seen in the next section, the reverse diffusion process is a useful metaphor in the discussion of deblurring.
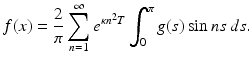
(5)
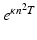 . Also note that the inverse problem is soluble only for a restricted class of functions g – those for which the series (5) converges in L 2[0, π]. As will be seen in the next section, the reverse diffusion process is a useful metaphor in the discussion of deblurring.
. Also note that the inverse problem is soluble only for a restricted class of functions g – those for which the series (5) converges in L 2[0, π]. As will be seen in the next section, the reverse diffusion process is a useful metaphor in the discussion of deblurring. Deblurring as an Inverse Problem
Cameras and other optical imagers capture a scene, or object, and convert it into an imperfect image. The object may be represented mathematically by a function f: R 2 → R that codes, for example, gray scale or intensity. The image produced by the device is a function g: R 2 → R, and the process may be phrased abstractly as g = Kf, where K is an operator modeling the operation of the imager. In a perfect imager, K = I, the identity operator (recall Mein Herr’s map!). The perfect model may be expressed in terms of the two-dimensional delta distribution as
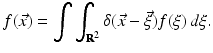 However, any physical imaging device blurs the object f into an image g, which in many cases can be represented by
However, any physical imaging device blurs the object f into an image g, which in many cases can be represented by
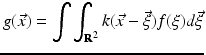
where k(⋅ ), the point spread function of the device, is some approximation of the delta function centered at the origin. Theoretical examples of such approximations include the tin-can function χ R ∕(π R 2), where χ R is the indicator function of the disk of radius R centered at the origin, and the sinc and sombrero functions given in polar coordinates by
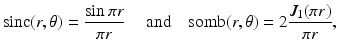 respectively, where J 1 is the Bessel function of first kind and order 1. A frequently occurring model uses the Gaussian point spread function
respectively, where J 1 is the Bessel function of first kind and order 1. A frequently occurring model uses the Gaussian point spread function
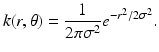 The problem of deblurring consists of solving (6) for the object f, given the blurred image g. For a good introduction to deblurring, see [44].
The problem of deblurring consists of solving (6) for the object f, given the blurred image g. For a good introduction to deblurring, see [44].
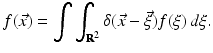
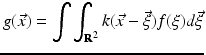
(6)
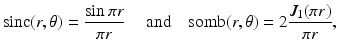
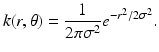
Reverse diffusion in two dimensions is a close cousin of deblurring. A basic tool in the analysis is the 2D Fourier transform defined for f: R 2 → R and 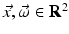 by
by
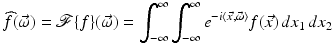 with the inversion formula
with the inversion formula
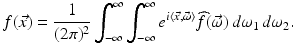 On integrating by parts, one sees that
On integrating by parts, one sees that
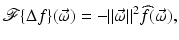 where
where 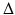 is the Laplacian operator:
is the Laplacian operator: 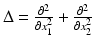 . Consider now the initial value problem for the 2D heat equation
. Consider now the initial value problem for the 2D heat equation
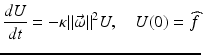 where
where 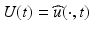 and hence
and hence 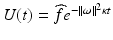 . The convolution theorem then gives
. The convolution theorem then gives
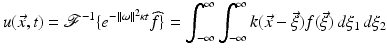
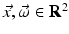 by
by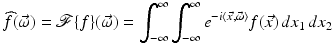
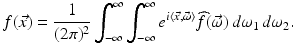
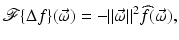
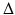 is the Laplacian operator:
is the Laplacian operator: 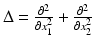 . Consider now the initial value problem for the 2D heat equation
. Consider now the initial value problem for the 2D heat equation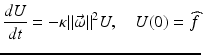
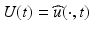 and hence
and hence 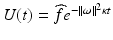 . The convolution theorem then gives
. The convolution theorem then gives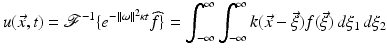
where (using the integral result of [25], 12.A)
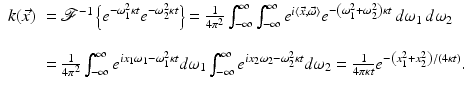 The inverse problem of determining the initial distribution
The inverse problem of determining the initial distribution 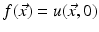 , given the distribution
, given the distribution 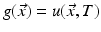 at a later time T > 0, is equivalent to solving the integral equation of the first kind
at a later time T > 0, is equivalent to solving the integral equation of the first kind
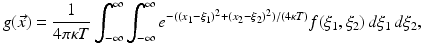 which is in turn equivalent to the deblurring problem with Gaussian point spread function
which is in turn equivalent to the deblurring problem with Gaussian point spread function
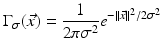 having variance σ 2 = 2κ T. The idea of deblurring by reverse diffusion is developed in [8].
having variance σ 2 = 2κ T. The idea of deblurring by reverse diffusion is developed in [8].
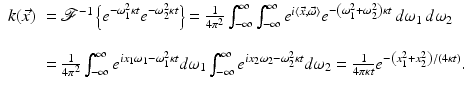
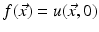 , given the distribution
, given the distribution 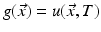 at a later time T > 0, is equivalent to solving the integral equation of the first kind
at a later time T > 0, is equivalent to solving the integral equation of the first kind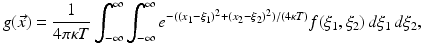
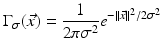
Extrapolation of Band-Limited Signals
Extrapolation is a basic challenge in signal analysis. The Fourier transform, 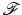 , is the analytical workhorse in this field. It transforms a time signal f(t), −∞ < t < ∞, into a complex-frequency distribution
, is the analytical workhorse in this field. It transforms a time signal f(t), −∞ < t < ∞, into a complex-frequency distribution 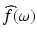 via the formula
via the formula
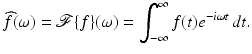 In a suitable setting, the time-to-frequency transformation may be inverted by the formula (e.g., [25])
In a suitable setting, the time-to-frequency transformation may be inverted by the formula (e.g., [25])
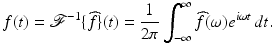 Any physically realizable detector is capable of picking up frequencies only in a limited range, say
Any physically realizable detector is capable of picking up frequencies only in a limited range, say 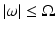 . A signal f whose Fourier transform vanishes for
. A signal f whose Fourier transform vanishes for ![$$\vert \omega \vert> \Omega $$” src=”/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_IEq31.gif”></SPAN>, for some given <SPAN id=IEq32 class=InlineEquation><IMG alt=]() 0$$” src=”/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_IEq32.gif”>, is called a band-limited signal. A detector that operates in the frequency band
0$$” src=”/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_IEq32.gif”>, is called a band-limited signal. A detector that operates in the frequency band 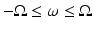 band-limits signals it collects, that is, it treats only
band-limits signals it collects, that is, it treats only ![$$\chi _{[-\Omega,\Omega ]}\widehat{f}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_IEq34.gif) , where
, where
![$$\displaystyle{\chi _{[-\Omega,\Omega ]}(\omega ) = \left \{\begin{array}{rc} 1,&\omega \in [-\Omega,\Omega ]\\ 0, & \omega \notin [-\Omega, \Omega ]. \end{array} \right.}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_Equan.gif) is the indicator function of the interval
is the indicator function of the interval ![$$[-\Omega,\Omega ]$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_IEq35.gif) . Multiplication by
. Multiplication by ![$$\chi _{[-\Omega,\Omega ]}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_IEq36.gif) in the frequency domain is called a low-pass filter as only components with frequency
in the frequency domain is called a low-pass filter as only components with frequency 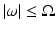 survive the filtering process.
survive the filtering process.
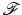 , is the analytical workhorse in this field. It transforms a time signal f(t), −∞ < t < ∞, into a complex-frequency distribution
, is the analytical workhorse in this field. It transforms a time signal f(t), −∞ < t < ∞, into a complex-frequency distribution 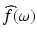 via the formula
via the formula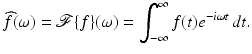
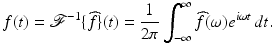
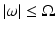 . A signal f whose Fourier transform vanishes for
. A signal f whose Fourier transform vanishes for 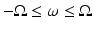 band-limits signals it collects, that is, it treats only
band-limits signals it collects, that is, it treats only ![$$\chi _{[-\Omega,\Omega ]}\widehat{f}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_IEq34.gif) , where
, where![$$\displaystyle{\chi _{[-\Omega,\Omega ]}(\omega ) = \left \{\begin{array}{rc} 1,&\omega \in [-\Omega,\Omega ]\\ 0, & \omega \notin [-\Omega, \Omega ]. \end{array} \right.}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_Equan.gif)
![$$[-\Omega,\Omega ]$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_IEq35.gif) . Multiplication by
. Multiplication by ![$$\chi _{[-\Omega,\Omega ]}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_IEq36.gif) in the frequency domain is called a low-pass filter as only components with frequency
in the frequency domain is called a low-pass filter as only components with frequency 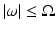 survive the filtering process.
survive the filtering process.Reconstruction of the full signal f is generally not possible as information in components with frequency greater than 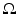 is unavailable. What is available is the signal
is unavailable. What is available is the signal
![$$\displaystyle{g = \mathcal{F}^{-1}\{\chi _{ [-\Omega,\Omega ]}\widehat{f}\}.}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_Equao.gif) By the convolution theorem for Fourier transforms, one then has
By the convolution theorem for Fourier transforms, one then has
![$$\displaystyle{g = \mathcal{F}^{-1}\{\chi _{ [-\Omega,\Omega ]}\} {\ast} f.}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_Equap.gif) However,
However,
![$$\displaystyle{\mathcal{F}^{-1}\{\chi _{ [-\Omega,\Omega ]}\}(t) = \frac{1} {2\pi }\int _{-\Omega }^{\Omega }e^{i\omega t}d\omega = \frac{\sin \Omega t} {\pi t}.}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_Equaq.gif) The reconstruction (or extrapolation) of the full signal f given the detected signal g requires the solution of the convolution equation
The reconstruction (or extrapolation) of the full signal f given the detected signal g requires the solution of the convolution equation
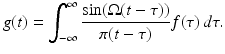 The problem of extrapolating a band-limited signal is then seen to be mathematically the same as deblurring the effect of an instrument with the one-dimensional point spread function
The problem of extrapolating a band-limited signal is then seen to be mathematically the same as deblurring the effect of an instrument with the one-dimensional point spread function
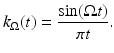
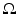 is unavailable. What is available is the signal
is unavailable. What is available is the signal![$$\displaystyle{g = \mathcal{F}^{-1}\{\chi _{ [-\Omega,\Omega ]}\widehat{f}\}.}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_Equao.gif)
![$$\displaystyle{g = \mathcal{F}^{-1}\{\chi _{ [-\Omega,\Omega ]}\} {\ast} f.}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_Equap.gif)
![$$\displaystyle{\mathcal{F}^{-1}\{\chi _{ [-\Omega,\Omega ]}\}(t) = \frac{1} {2\pi }\int _{-\Omega }^{\Omega }e^{i\omega t}d\omega = \frac{\sin \Omega t} {\pi t}.}$$](/wp-content/uploads/2016/04/A183156_2_En_1_Chapter_Equaq.gif)
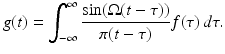
PET
CT scanning with X-rays is an instance of transmission tomography. A decade and a half prior to Cormack’s publications on transmission tomography, an emission tomography technique, now known as PET (positron transmission tomography), was proposed [72]. In PET, a metabolically active tracer in the form of a positron-emitting isotope is injected into an area for which it has an affinity and taken up (metabolized) by an organ. The isotope emits positrons that immediately combine with free electrons in so-called annihilation events, which result in the ejection of two photons (γ-rays) along oppositely directed collinear rays. When a pair of detectors located on an array surrounding the body pick up the simultaneous arrival of two photons, one at each detector, respectively, an annihilation event is assumed to have taken place on the segment connecting the two detectors. In PET, the data collected from a very large number of such events is used to construct a two-dimensional tomographic slice of the isotope distribution. Because the uptake of the isotope is metabolically driven, PET is an effective tool for studying metabolism giving it a diagnostic advantage over X-ray CT scanning. A combination of an X-ray CT scan with a PET scan provides the diagnostician anatomical information (distribution of attenuation coefficient) and physiological information (density of metabolized tracer isotope), respectively.
If f: R 2 → R (we consider only a simplified version of 2D-PET) is the density of the metabolized tracer isotope, then the number of annihilations occurring along the coincidence line L connecting two detectors is proportional to the line integral
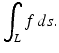 That is, the observed counts of annihilation events are measured by the Radon transform of the density f. However, this does not take account of attenuation effects and can under represent features of deep-seated tissue. If the attenuation distribution is μ(⋅, ⋅ ), and the pair of photons resulting from an annihilation event on the coincidence line L traverse oppositely directed rays L + and L − of L, emanating from the annihilation site, then the detected attenuated signal takes the form
That is, the observed counts of annihilation events are measured by the Radon transform of the density f. However, this does not take account of attenuation effects and can under represent features of deep-seated tissue. If the attenuation distribution is μ(⋅, ⋅ ), and the pair of photons resulting from an annihilation event on the coincidence line L traverse oppositely directed rays L + and L − of L, emanating from the annihilation site, then the detected attenuated signal takes the form
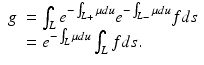 The model operator may now be viewed as a bivariate operator K(μ, f) = g, in which the operator K(⋅, f) is nonlinear and the operator K(μ, ⋅ ) is linear. In soft tissue the attenuation coefficient is essentially zero, and therefore the solution of the inverse problem is accomplished by a Radon inversion of K(0, ⋅ ). PET scans may be performed in combination with X-ray CT scans; the CT scan provides the attenuation coefficient, which may then be used in the model above to find the isotope density. See [52] for an extensive survey of emission tomography.
The model operator may now be viewed as a bivariate operator K(μ, f) = g, in which the operator K(⋅, f) is nonlinear and the operator K(μ, ⋅ ) is linear. In soft tissue the attenuation coefficient is essentially zero, and therefore the solution of the inverse problem is accomplished by a Radon inversion of K(0, ⋅ ). PET scans may be performed in combination with X-ray CT scans; the CT scan provides the attenuation coefficient, which may then be used in the model above to find the isotope density. See [52] for an extensive survey of emission tomography.
Some Mathematics for Inverse Problems
 Philosophy is written in that great book which ever lies before our Philoso Philosophy is written in that great book which ever lies before our
Philosophy is written in that great book which ever lies before our Philoso Philosophy is written in that great book which ever lies before our gaze – I mean the universe …. The book is written in the
mathematical language …without which one wanders
in vain through a dark labyrinth.
Galileo Galilei
Hilbert space is a familiar environment that is rich enough for a discussion of the chief mathematical issues that are important in the theory of inverse problems. For the most part we restrict our attention to real Hilbert spaces. The inner product and associated norm will be symbolized by 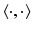 and
and 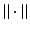 , respectively:
, respectively:
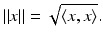 We assume the reader is familiar with the basic properties of inner product spaces (see, e.g., [18, Chap. I]), including the Cauchy–Schwarz inequality
We assume the reader is familiar with the basic properties of inner product spaces (see, e.g., [18, Chap. I]), including the Cauchy–Schwarz inequality
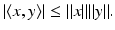
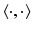 and
and 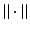 , respectively:
, respectively: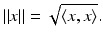
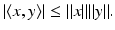
A Hilbert space H is complete, that is, Cauchy sequences in H converge:
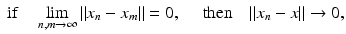 for some x ∈ H. The smallest (in the sense of inclusion) Hilbert space that contains a given inner product space is known as the completion of the inner product space. (Every inner product space has a unique completion.)
for some x ∈ H. The smallest (in the sense of inclusion) Hilbert space that contains a given inner product space is known as the completion of the inner product space. (Every inner product space has a unique completion.)
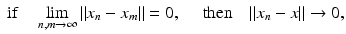
The space, denoted L 2[a, b




Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree



