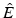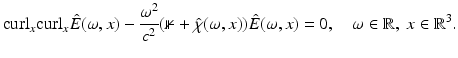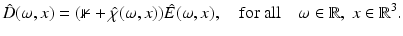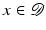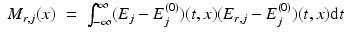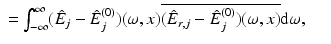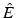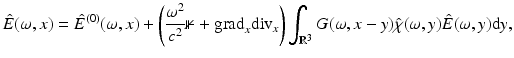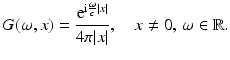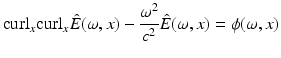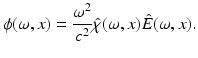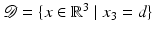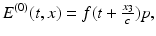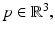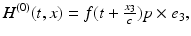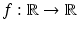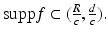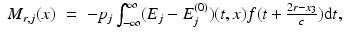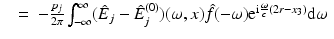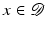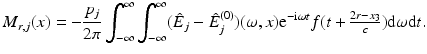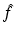Fig. 1
Schematic diagram of the light traveling in an OCT system. The laser beam emitted by the source is divided at the beam splitter into two light beams; one is reflected at a mirror, the other one backscattered from the sample. The superposition of the two reflected beams is then measured at the detector
There exist different variants of the OCT regarding the way the measurements are done:
Time and frequency domain OCT:
In time domain OCT, the position of the mirror is varied and for each position one measurement is performed. On the other hand, in frequency domain OCT, the reference mirror is fixed and the detector is replaced by a spectrometer. Both methods provide equivalent measurements which are connected by a Fourier transform.
Standard and full field OCT:
In standard OCT, the incoming light is focused through objective lenses to one spot in a certain depth in the sample and the backscattered light is measured in a point detector. This means that to obtain information of the whole sample, a transversal-lateral scan has to be performed (by moving the light beam over the frontal surface of the sample). In full field OCT, the entire frontal surface of the sample is illuminated at once and the single point detector is replaced by a two-dimensional detector array, for instance by a charge-coupled device (CCD) camera.
Polarization-sensitive OCT:
In classical OCT setups, the electromagnetic wave is simply treated as a scalar quantity. In polarization-sensitive OCT, however, the illuminating light beams are polarized and the detectors measure the intensity of the two polarization components of the interfered light.
There are also further modifications such as Doppler OCT and quantum OCT, which are not addressed here. In this chapter, the focus is mainly on time domain full field OCT, but also the others are discussed.
3 The Direct Scattering Problem
To derive a mathematical model for an OCT system, one has to describe on one hand the propagation and the scattering of the laser beam in the presence of the sample and on the other hand the way how this scattered wave is measured at the detectors. For the first part, the interaction of the incoming light with the sample can be modeled with Maxwell’s macroscopic equations.
Maxwell’s Equations
Maxwell’s equations in matter consist of the partial differential equations



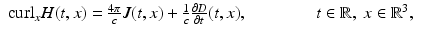
relating the following physical quantities (at some time 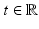 and some location
and some location 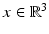 ):
):

(1a)

(1b)

(1c)
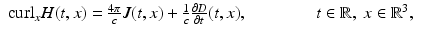
(1d)
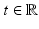 and some location
and some location 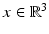 ):
):Speed of light | c | 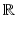 |
External charge density | ρ(t, x) | 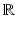 |
External electric current density | J(t, x) | 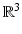 |
Electric field | E(t, x) | 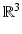 |
Electric displacement | D(t, x) | 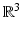 |
Magnetic induction | B(t, x) | 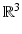 |
Magnetic field | H(t, x) | 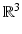 |
Maxwell’s equations do not yet completely describe the propagation of the light (even assuming that the charge density ρ and the current density J are known, there are only 8 equations for the 12 unknowns E, D, B, and H).
Additionally to Maxwell’s equations, it is therefore necessary to specify the relations between the fields D and E as well as between B and H.
Let 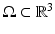 denote the domain where the sample is located. It is considered as a nonmagnetic, dielectric medium without external charges or currents, this means that for all
denote the domain where the sample is located. It is considered as a nonmagnetic, dielectric medium without external charges or currents, this means that for all  and all
and all 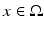 the electric and magnetic fields fulfil the relations
the electric and magnetic fields fulfil the relations
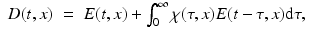
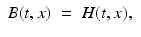
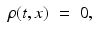
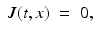
where the function 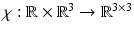 (for convenience, χ is also defined for negative times by χ(t, x) = 0 for t < 0,
(for convenience, χ is also defined for negative times by χ(t, x) = 0 for t < 0, 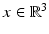 ) is called the (electric) susceptibility and is the quantity to be recovered. The time dependence of χ hereby describes the fact that a change in the electric field E cannot immediately cause a change in the electric displacement D. Since this delay is quite small, it is sometimes ignored and χ(t, x) is then replaced by δ(t)χ(x). Moreover, the medium is often considered to be isotropic, which means that χ is a multiple of the identity matrix.
) is called the (electric) susceptibility and is the quantity to be recovered. The time dependence of χ hereby describes the fact that a change in the electric field E cannot immediately cause a change in the electric displacement D. Since this delay is quite small, it is sometimes ignored and χ(t, x) is then replaced by δ(t)χ(x). Moreover, the medium is often considered to be isotropic, which means that χ is a multiple of the identity matrix.
 denote the domain where the sample is located. It is considered as a nonmagnetic, dielectric medium without external charges or currents, this means that for all
denote the domain where the sample is located. It is considered as a nonmagnetic, dielectric medium without external charges or currents, this means that for all 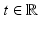 and all
and all 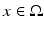 the electric and magnetic fields fulfil the relations
the electric and magnetic fields fulfil the relations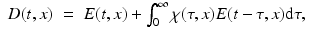
(2a)
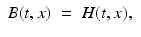
(2b)
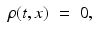
(2c)
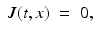
(2d)
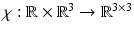 (for convenience, χ is also defined for negative times by χ(t, x) = 0 for t < 0,
(for convenience, χ is also defined for negative times by χ(t, x) = 0 for t < 0, 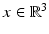 ) is called the (electric) susceptibility and is the quantity to be recovered. The time dependence of χ hereby describes the fact that a change in the electric field E cannot immediately cause a change in the electric displacement D. Since this delay is quite small, it is sometimes ignored and χ(t, x) is then replaced by δ(t)χ(x). Moreover, the medium is often considered to be isotropic, which means that χ is a multiple of the identity matrix.
) is called the (electric) susceptibility and is the quantity to be recovered. The time dependence of χ hereby describes the fact that a change in the electric field E cannot immediately cause a change in the electric displacement D. Since this delay is quite small, it is sometimes ignored and χ(t, x) is then replaced by δ(t)χ(x). Moreover, the medium is often considered to be isotropic, which means that χ is a multiple of the identity matrix.The sample is situated in vacuum and the assumptions (2) are modified by setting for all 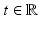 and all
and all 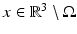
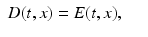
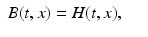
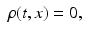
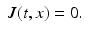
This simply corresponds to extend the Eq. (2) to  and to assume χ(t, x) = 0 for all
and to assume χ(t, x) = 0 for all  ,
, 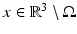 .
.
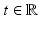 and all
and all 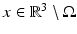
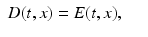
(3a)
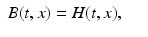
(3b)
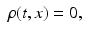
(3c)
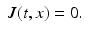
(3d)
 and to assume χ(t, x) = 0 for all
and to assume χ(t, x) = 0 for all 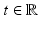 ,
, 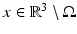 .
.In this case of a nonmagnetic medium, Maxwell’s equations result into one equation for the electric field E. To get rid of the convolution in (2a), it is practical to consider the Fourier transform with respect to time. In the following, the convention
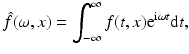 for the Fourier transform of a function f with respect to t is used.
for the Fourier transform of a function f with respect to t is used.
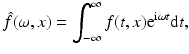
Proposition 1.
Proof.
Initial Conditions
The sample is illuminated with a laser beam described initially (before it interacts with the sample) by the electric field 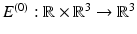 which is (together with some magnetic field) a solution of Maxwell’s equations (1) with the assumptions (3) for all
which is (together with some magnetic field) a solution of Maxwell’s equations (1) with the assumptions (3) for all 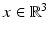 . Then, it follows from the proof of the 1, for χ = 0, that
. Then, it follows from the proof of the 1, for χ = 0, that
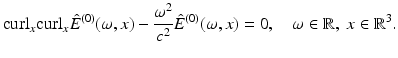
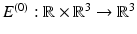 which is (together with some magnetic field) a solution of Maxwell’s equations (1) with the assumptions (3) for all
which is (together with some magnetic field) a solution of Maxwell’s equations (1) with the assumptions (3) for all 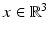 . Then, it follows from the proof of the 1, for χ = 0, that
. Then, it follows from the proof of the 1, for χ = 0, that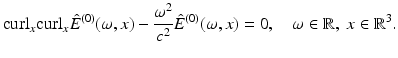
(6)
Moreover, it is assumed that E (0) does not interact with the sample until the time t = 0, which means that supp 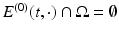 for all t ≤ 0.
for all t ≤ 0.
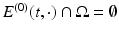 for all t ≤ 0.
for all t ≤ 0.The electric field 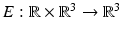 generated by this incoming light beam in the presence of the sample is then a solution of Maxwell’s equations (1) with the assumptions (2) and the initial condition
generated by this incoming light beam in the presence of the sample is then a solution of Maxwell’s equations (1) with the assumptions (2) and the initial condition
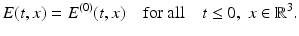
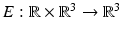 generated by this incoming light beam in the presence of the sample is then a solution of Maxwell’s equations (1) with the assumptions (2) and the initial condition
generated by this incoming light beam in the presence of the sample is then a solution of Maxwell’s equations (1) with the assumptions (2) and the initial condition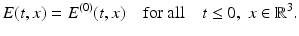
(7)
Since Maxwell’s equations for E in 1 are reformulated as an equation for the Fourier transform 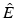 , it is helpful to rewrite the initial condition in terms of
, it is helpful to rewrite the initial condition in terms of 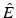 .
.
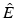 , it is helpful to rewrite the initial condition in terms of
, it is helpful to rewrite the initial condition in terms of 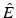 .
.Proposition 2.
Let E (together with some magnetic field H) fulfil Maxwell’s equations (1) with the assumptions (2) and (3) and with the initial condition (7) .
Then the Fourier transform of E − E (0) fulfils that the function 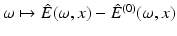 , defined on
, defined on 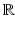 , can be extended to a square integrable, holomorphic function on the upper half plane
, can be extended to a square integrable, holomorphic function on the upper half plane 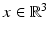 .
.
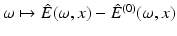 , defined on
, defined on 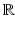 , can be extended to a square integrable, holomorphic function on the upper half plane
, can be extended to a square integrable, holomorphic function on the upper half plane 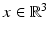 .
.Proof.
From the initial condition (7) it follows that E(t, x) − E (0)(t, x) = 0 for all t ≤ 0. Thus, the result is a direct consequence form the Paley–Wiener theorem, which is based on the fact that in this case
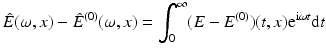 is well defined for all
is well defined for all 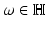 and complex differentiable with respect to
and complex differentiable with respect to 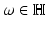 . □
. □
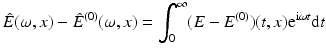
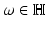 and complex differentiable with respect to
and complex differentiable with respect to 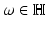 . □
. □ The Measurements
The measurements are obtained by the combination of the backscattered field from the sample and the back-reflected field from the mirror. In practice, see Fig. 1, the sample and the mirror are in different positions. However, without loss of generality, a placement of them around the origin is assumed in the proposed formulation, in order to avoid rotating the coordinate system. To do so, the simultaneously illumination of the sample and the mirror is suppressed and two different illumination schemes are considered. The gain is to keep the same coordinate system but the reader should not be confused with illumination at different times.
Thus, the electric field E, which is obtained by illuminating the sample with the initial field E (0) (that is E solves (4) with the initial condition (7)), is combined with E r which is the electric field obtained by replacing the sample by a mirror and illuminating with the same initial field E (0).
The mirror is placed orthogonal to the unit vector e 3 = (0, 0, 1) through the point re 3. As in (7), it is assumed that supp E (0)(t, ⋅ ) does not interact with the mirror for t < 0, so that
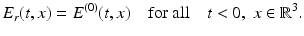
Then the resulting electric field 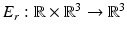 is given as the solution of the same equations as E (Maxwell’s equations (1) together with the assumptions (2) and initial condition (8)) with the susceptibility χ replaced by the susceptibility χ r of the mirror at position r. One sort of (ideal) mirror can be described via the susceptibility χ r (t, x) = 0 for x 3 > r and
is given as the solution of the same equations as E (Maxwell’s equations (1) together with the assumptions (2) and initial condition (8)) with the susceptibility χ replaced by the susceptibility χ r of the mirror at position r. One sort of (ideal) mirror can be described via the susceptibility χ r (t, x) = 0 for x 3 > r and 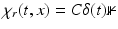 for x 3 ≤ r with an (infinitely) large constant C > 0.
for x 3 ≤ r with an (infinitely) large constant C > 0.
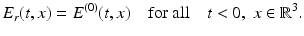
(8)
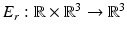 is given as the solution of the same equations as E (Maxwell’s equations (1) together with the assumptions (2) and initial condition (8)) with the susceptibility χ replaced by the susceptibility χ r of the mirror at position r. One sort of (ideal) mirror can be described via the susceptibility χ r (t, x) = 0 for x 3 > r and
is given as the solution of the same equations as E (Maxwell’s equations (1) together with the assumptions (2) and initial condition (8)) with the susceptibility χ replaced by the susceptibility χ r of the mirror at position r. One sort of (ideal) mirror can be described via the susceptibility χ r (t, x) = 0 for x 3 > r and 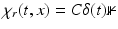 for x 3 ≤ r with an (infinitely) large constant C > 0.
for x 3 ≤ r with an (infinitely) large constant C > 0.The intensity I r of each component of the superposition of the electric fields E and E r averaged over all time is measured at some detector points. The detectors are positioned at all points on the plane
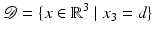 parallel to the mirror at a distance d > 0 from the origin. The mirror and the sample are both located in the lower half plane of the detector surface with some minimal distance to
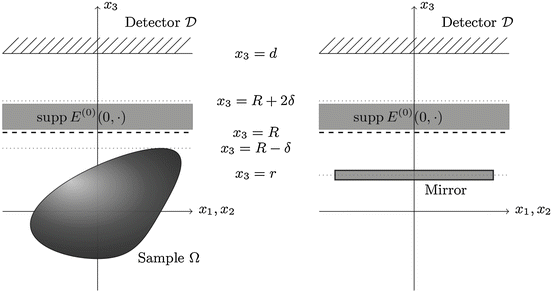
parallel to the mirror at a distance d > 0 from the origin. The mirror and the sample are both located in the lower half plane of the detector surface with some minimal distance to 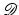 . Moreover, the highest possible position R ∈ (δ, d − 2δ) of the mirror shall be by some distance δ > 0 closer to the detector than the sample, this means (see Fig. 2)
. Moreover, the highest possible position R ∈ (δ, d − 2δ) of the mirror shall be by some distance δ > 0 closer to the detector than the sample, this means (see Fig. 2)
 . Moreover, the highest possible position R ∈ (δ, d − 2δ) of the mirror shall be by some distance δ > 0 closer to the detector than the sample, this means (see Fig. 2)
. Moreover, the highest possible position R ∈ (δ, d − 2δ) of the mirror shall be by some distance δ > 0 closer to the detector than the sample, this means (see Fig. 2)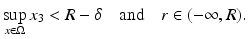
(9)

Fig. 2
The two scattering problems involved in OCT: On the left hand side the scattering of the initial wave on the sample  ; on the right hand side the reference problem where the initial wave E (0) is reflected by a perfect mirror at a tunable position r ∈ (−∞, R). The two resulting electric fields, E and E r , are then combined and this superposition E + E r is measured at the detector surface
; on the right hand side the reference problem where the initial wave E (0) is reflected by a perfect mirror at a tunable position r ∈ (−∞, R). The two resulting electric fields, E and E r , are then combined and this superposition E + E r is measured at the detector surface 
 ; on the right hand side the reference problem where the initial wave E (0) is reflected by a perfect mirror at a tunable position r ∈ (−∞, R). The two resulting electric fields, E and E r , are then combined and this superposition E + E r is measured at the detector surface
; on the right hand side the reference problem where the initial wave E (0) is reflected by a perfect mirror at a tunable position r ∈ (−∞, R). The two resulting electric fields, E and E r , are then combined and this superposition E + E r is measured at the detector surface 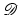
To simplify the argument, let us additionally assume that the incoming electric field E (0) does not influence the detector after the time t = 0, meaning that
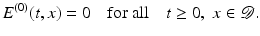
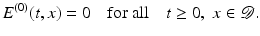
(10)
At the detector array, the data are obtained by measuring
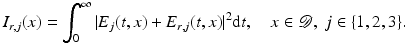
In standard OCT, the polarization is usually ignored. In this case, only the total intensity 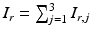 needs to be measured, see Sect. 5 for the reconstruction formulas in the isotropic case.
needs to be measured, see Sect. 5 for the reconstruction formulas in the isotropic case.
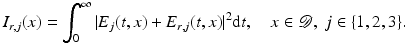
(11)
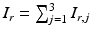 needs to be measured, see Sect. 5 for the reconstruction formulas in the isotropic case.
needs to be measured, see Sect. 5 for the reconstruction formulas in the isotropic case.In this measurement setup, it is easy to acquire besides the intensity I r also the intensity of the two waves E and E r separately by blocking one of the two waves E and E r at a time. Practically, it is sometimes not even necessary to measure them since the intensity of the reflected laser beam E r can be explicitly calculated from the knowledge of the initial beam E (0), and the intensity of E is usually negligible compared with the intensity I r (because of the assumption (10), the field E contains only backscattered light at the detector after the measurement starts). Therefore, one can consider instead of I r the function
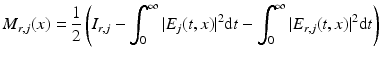
for r ∈ (−∞, R), j ∈ { 1, 2, 3}, and 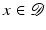 as the measurement data.
as the measurement data.
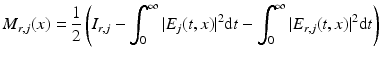
(12)
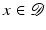 as the measurement data.
as the measurement data.Proposition 3.
Proof.
Expanding the function I r, j , given by (11), gives
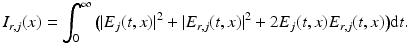 Thus, by the Definition (12) of M r , it follows that
Thus, by the Definition (12) of M r , it follows that
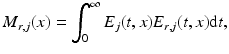 which, using the assumption (10), can be rewritten in the form
which, using the assumption (10), can be rewritten in the form
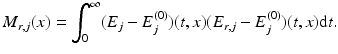 Then, since E and E r coincide with E (0) for t < 0, see (7) and (8), the integration can be extended to all times. This proves the formula (13a) for M r . The second formula follows from Plancherel’s theorem. □
Then, since E and E r coincide with E (0) for t < 0, see (7) and (8), the integration can be extended to all times. This proves the formula (13a) for M r . The second formula follows from Plancherel’s theorem. □
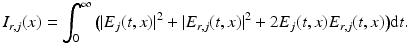
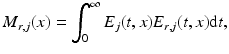
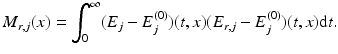
4 Solution of the Direct Problem
In this section the solution of the direct problem, to determine the measurements M r , defined by (13a), from the susceptibility χ, is derived using Born and far field approximation for the electric field.
Proposition 4.
Proof.
Using that 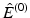 solves (6), the difference
solves (6), the difference 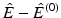 satisfies the inhomogeneous vector Helmholtz equation
satisfies the inhomogeneous vector Helmholtz equation
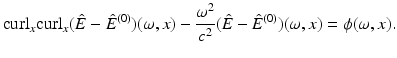
The divergence of this equation, using that 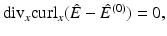 implies
implies
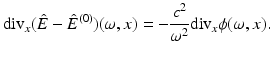
Applying the vector identity
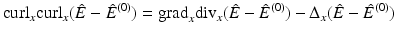 in (16) and using (17) yields
in (16) and using (17) yields
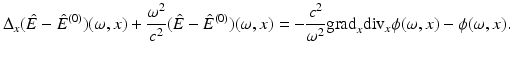 This is a Helmholtz equation for
This is a Helmholtz equation for 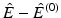 and the general solution which is (with respect to ω) holomorphic in the upper half plane (equivalent to (7) by 2) is given by, see [8]
and the general solution which is (with respect to ω) holomorphic in the upper half plane (equivalent to (7) by 2) is given by, see [8]
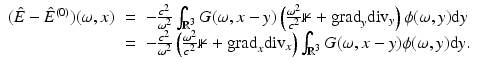 For the last equality, integration by parts and
For the last equality, integration by parts and 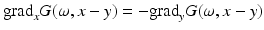 were used. The Lippmann–Schwinger equation (14) follows from the last expression inserting the expression (15) for ϕ. □
were used. The Lippmann–Schwinger equation (14) follows from the last expression inserting the expression (15) for ϕ. □
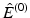 solves (6), the difference
solves (6), the difference 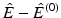 satisfies the inhomogeneous vector Helmholtz equation
satisfies the inhomogeneous vector Helmholtz equation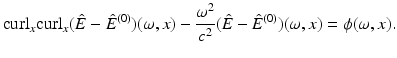
(16)
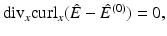 implies
implies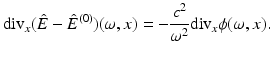
(17)
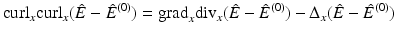
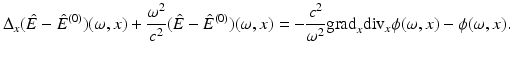
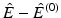 and the general solution which is (with respect to ω) holomorphic in the upper half plane (equivalent to (7) by 2) is given by, see [8]
and the general solution which is (with respect to ω) holomorphic in the upper half plane (equivalent to (7) by 2) is given by, see [8]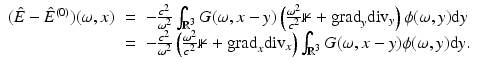
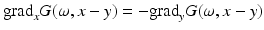 were used. The Lippmann–Schwinger equation (14) follows from the last expression inserting the expression (15) for ϕ. □
were used. The Lippmann–Schwinger equation (14) follows from the last expression inserting the expression (15) for ϕ. □ This integral equation uniquely defines the electric field E. The reader is referred to [1, 8] for the isotropic case and to [33] for an anisotropic medium.
Born and Far Field Approximation
To solve the Lippmann–Schwinger equation (14), the medium is assumed to be weakly scattering, which means that 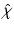 is sufficiently small (implying that the difference
is sufficiently small (implying that the difference 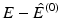 becomes small compared to E (0)) so that the Born approximation E (1), defined by
becomes small compared to E (0)) so that the Born approximation E (1), defined by
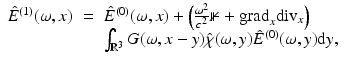
is considered a good approximation for the electric field E, see [3]. To describe multiple scattering events, one considers higher order Born approximations. For different linearization techniques, the reader is referred to [1, 23]. Moreover, since the detector in OCT is typically quite far away from the sample, one can simplify the expression (18) for the electric field at the detector array by replacing it with its asymptotic behavior for | x | → ∞, that is replace the formula for E (1) by its far field approximation (the far field approximation could also be applied to the solution E of the Lippmann–Schwinger equation (14)).
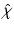 is sufficiently small (implying that the difference
is sufficiently small (implying that the difference 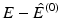 becomes small compared to E (0)) so that the Born approximation E (1), defined by
becomes small compared to E (0)) so that the Born approximation E (1), defined by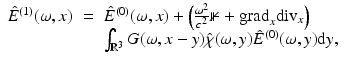
(18)
Proposition 5.
Consider, for a given function 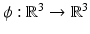 with compact support and some parameter
with compact support and some parameter 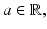 the function
the function
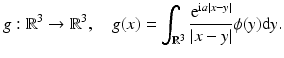 Then, it follows, asymptotically for ρ →∞ and uniformly in
Then, it follows, asymptotically for ρ →∞ and uniformly in 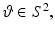 that
that
![$$\displaystyle{ (a^{2} + {\mathrm{grad}}_{ x}{\mathrm{div}}_{x})g(\rho \vartheta ) \simeq -\frac{a^{2}{\mathrm{e}}^{{\mathrm{i}}a\rho }} {\rho } \int _{\mathbb{R}^{3}}\vartheta \times (\vartheta \times \phi (y)){\mathrm{e}}^{-{\mathrm{i}}a\left <\vartheta,y\right >}{\mathrm{d}}y }$$” src=”/wp-content/uploads/2016/04/A183156_2_En_44_Chapter_Equ30.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(19)</DIV></DIV></DIV></DIV><br />
<DIV class=]()
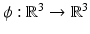 with compact support and some parameter
with compact support and some parameter 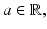 the function
the function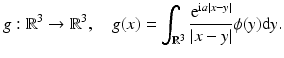
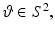 that
thatProof.
Consider the function
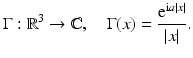 Then
Then
![$$\displaystyle\begin{array}{rcl} \frac{\partial ^{2}\Gamma } {\partial x_{j}\partial x_{k}}(x)& =& \frac{\partial } {\partial x_{j}}\left [\left ( \frac{{\mathrm{i}}a} {\vert x\vert ^{2}} - \frac{1} {\vert x\vert ^{3}}\right )x_{k}{\mathrm{e}}^{{\mathrm{i}}a\vert x\vert }\right ] {}\\ & =& \left [\left ( \frac{{\mathrm{i}}a} {\vert x\vert ^{2}} - \frac{1} {\vert x\vert ^{3}}\right )\delta _{jk} + \left ( \frac{{\mathrm{i}}a} {\vert x\vert ^{2}} - \frac{1} {\vert x\vert ^{3}}\right )\frac{{\mathrm{i}}ax_{j}x_{k}} {\vert x\vert } \right. {}\\ & & +\left.\left (-2 \frac{{\mathrm{i}}a} {\vert x\vert ^{3}} + 3 \frac{1} {\vert x\vert ^{4}}\right )\frac{x_{j}x_{k}} {\vert x\vert } \right ]{\mathrm{e}}^{{\mathrm{i}}a\vert x\vert }. {}\\ \end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_44_Chapter_Equ31.gif) Therefore, writing x in spherical coordinates:
Therefore, writing x in spherical coordinates: 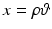 with ρ > 0,
with ρ > 0,  , for ρ → ∞ uniformly in
, for ρ → ∞ uniformly in  it can be seen that
it can be seen that
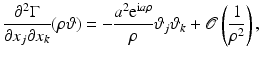 The approximation (locally uniformly in
The approximation (locally uniformly in 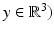
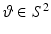 )
)
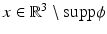
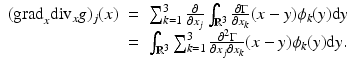 Asymptotically for | x | → ∞ (again using the compact support of ϕ) one obtains
Asymptotically for | x | → ∞ (again using the compact support of ϕ) one obtains
![$$\displaystyle{a^{2}g_{ j}(\rho \vartheta ) + ({\mathrm{grad}}_{x}{\mathrm{div}}_{x}g)_{j}(\rho \vartheta ) \simeq a^{2}\int _{ \mathbb{R}^{3}}\sum _{k=1}^{3}\frac{{\mathrm{e}}^{{\mathrm{i}}a(\rho -\left <\vartheta,y\right >)}} {\rho } \left (\delta _{jk} -\vartheta _{j}\vartheta _{k}\right )\phi _{k}(y){\mathrm{d}}y.}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_44_Chapter_Equq.gif”></DIV></DIV></DIV>The approximation (<SPAN class=InternalRef><A href=]() 19) follows from the vector identity
19) follows from the vector identity 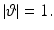 □
□
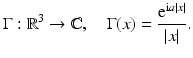
![$$\displaystyle\begin{array}{rcl} \frac{\partial ^{2}\Gamma } {\partial x_{j}\partial x_{k}}(x)& =& \frac{\partial } {\partial x_{j}}\left [\left ( \frac{{\mathrm{i}}a} {\vert x\vert ^{2}} - \frac{1} {\vert x\vert ^{3}}\right )x_{k}{\mathrm{e}}^{{\mathrm{i}}a\vert x\vert }\right ] {}\\ & =& \left [\left ( \frac{{\mathrm{i}}a} {\vert x\vert ^{2}} - \frac{1} {\vert x\vert ^{3}}\right )\delta _{jk} + \left ( \frac{{\mathrm{i}}a} {\vert x\vert ^{2}} - \frac{1} {\vert x\vert ^{3}}\right )\frac{{\mathrm{i}}ax_{j}x_{k}} {\vert x\vert } \right. {}\\ & & +\left.\left (-2 \frac{{\mathrm{i}}a} {\vert x\vert ^{3}} + 3 \frac{1} {\vert x\vert ^{4}}\right )\frac{x_{j}x_{k}} {\vert x\vert } \right ]{\mathrm{e}}^{{\mathrm{i}}a\vert x\vert }. {}\\ \end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_44_Chapter_Equ31.gif)
 with ρ > 0,
with ρ > 0,  , for ρ → ∞ uniformly in
, for ρ → ∞ uniformly in 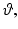 it can be seen that
it can be seen that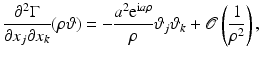
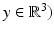
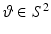 )
)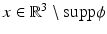
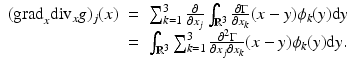
 □
□ The application of both the far field and the Born approximation, this means 5 for the expression (18) of E (1), that is setting a = ω∕c and 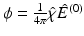 in 5, imply the asymptotic behavior
in 5, imply the asymptotic behavior
![$$\displaystyle{ \hat{E}^{(1)}(\omega,\rho \vartheta ) \simeq \hat{ E}^{(0)}(\omega,\rho \vartheta ) -\frac{\omega ^{2}{\mathrm{e}}^{{\mathrm{i}} \frac{\omega } {c}\rho }} {4\pi \rho c^{2}} \int _{\mathbb{R}^{3}}\vartheta \times \big (\vartheta \times (\hat{\chi }(\omega,y)\hat{E}^{(0)}(\omega,y))\big){\mathrm{e}}^{-{\mathrm{i}} \frac{\omega } {c}\left <\vartheta,y\right >}{\mathrm{d}}y. }$$” src=”/wp-content/uploads/2016/04/A183156_2_En_44_Chapter_Equ33.gif”></DIV></DIV><br />
<DIV class=EquationNumber>(20)</DIV></DIV></DIV></DIV><br />
<DIV id=Sec9 class=]()
Maxwell’s equations (1) in the vacuum, that is with the additional assumptions (3) .
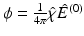 in 5, imply the asymptotic behavior
in 5, imply the asymptotic behaviorThe Forward Operator
To obtain a forward model for the measurements described in Sect. 3, the (approximative) formula (20) is considered as a model for the solution of the scattering problem. To make this formula concrete, one has to plug in a function E (0) describing the initial illumination (recall that E (0) has to solve (6)).
Proof.
The four equations of (1) can be directly verified:
Get Clinical Tree app for offline access

In the case of an illumination E (0) of the form (21), the electric field E r produced by an ideal mirror at the position r is given by
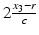 . The change in polarization of the reflected wave (from p to − p) comes from the fact that the tangential components of the electric field have to be continuous across the border of the mirror.
. The change in polarization of the reflected wave (from p to − p) comes from the fact that the tangential components of the electric field have to be continuous across the border of the mirror.




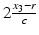 . The change in polarization of the reflected wave (from p to − p) comes from the fact that the tangential components of the electric field have to be continuous across the border of the mirror.
. The change in polarization of the reflected wave (from p to − p) comes from the fact that the tangential components of the electric field have to be continuous across the border of the mirror.The following proposition gives the form of the measurements M r , described in Sect. 3, on the detector surface  for the specific illumination (21).
for the specific illumination (21).
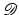 for the specific illumination (21).
for the specific illumination (21).Proposition 7.
Proof.
Since the electric field E r reflected on a mirror at vertical position r ∈ (−∞, R) is according to (23) given by
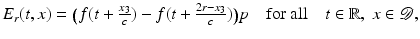 the measurement functions M r (defined by (12) and computed with (13a)) are simplified, for the particular initial illumination E (0) of the form (21), to (24a) for
the measurement functions M r (defined by (12) and computed with (13a)) are simplified, for the particular initial illumination E (0) of the form (21), to (24a) for 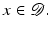
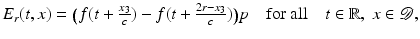
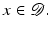
In the limiting case of a delta impulse as initial wave, that is for f(ξ) = δ(ξ −ξ 0) with some constant 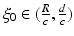 satisfying (22), the measurements provide directly the electric field. Indeed, it can be seen from (24a) that
satisfying (22), the measurements provide directly the electric field. Indeed, it can be seen from (24a) that
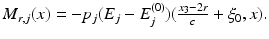 By varying r ∈ (−∞, R), the electric field E can be obtained (to be more precise, its component in direction of the initial polarization) as a function of time at every detector position.
By varying r ∈ (−∞, R), the electric field E can be obtained (to be more precise, its component in direction of the initial polarization) as a function of time at every detector position.
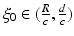 satisfying (22), the measurements provide directly the electric field. Indeed, it can be seen from (24a) that
satisfying (22), the measurements provide directly the electric field. Indeed, it can be seen from (24a) that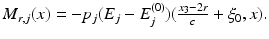
The following assumptions are made:
Assumption 1.
The susceptibility χ is sufficiently small so that the Born approximation E (1) for the solution E of the Lippmann–Schwinger equation ( 14 ) can be applied.
Assumption 2.
The detectors are sufficiently far away from the object so that one can use the far field asymptotics ( 20 ) for the measured field.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree