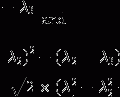([1])
where B 0 is the strength of the external magnetic field (measured in Tesla), ω 0 and ν 0 are the angular velocity and frequency of the precession, respectively, and γ is the gyromagnetic ratio, depending only on the nuclear species. ν 0 is called the Larmor frequency for the given nucleus at field B 0. Table 1 contains the gyromagnetic ratios for a few of the most used nuclei in NMR.
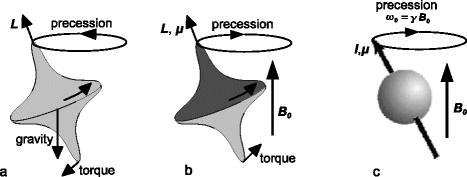
Fig. 1.
Precession of (a) a spinning top with angular momentum L under the influence of gravity, (b) a magnetic top with angular momentum L and magnetic moment μ inside a magnetic field and (c) a nucleus with spin I and an associated magnetic moment μ inside a magnetic field B 0.
Table 1
Gyromagnetic ratio, spin quantum number and natural abundance of some of the most used nuclei in in vivo NMR
Nucleus | γ [106 rad/T] | γ/2π [MHz/T] | Spin | Natural abundance [%] |
|---|---|---|---|---|
1H | 267.522 | 42.576 | 1/2 | 100 |
2H | 41.066 | 6.536 | 1 | 0.015 |
13C | 67.283 | 10.705 | 1/2 | 1.1 |
19F | 251.815 | 40.078 | 1/2 | 100 |
31P | 108.394 | 17.235 | 1/2 | 100 |
23Na | 70.808 | 11.262 | 3/2 | 100 |
17O | −36.281 | −5.7716 | 5/2 | 0.04 |
3He | −203.789 | −32.434 | 1/2 | 100 |
129Xe | −74.521 | −11.777 | 1/2 | 24.4 |
In contrast to the spinning top, the nucleus is subject to the laws of quantum mechanics, which change its behaviour in many ways. The analogy of the magnetic top, however, can be (and effectively is often) used to qualitatively describe many of the phenomena associated with NMR.
2.1 Zeeman Effect
For a better understanding of the principles of nuclear magnetism, a short look into the quantum mechanical properties of atomic nuclei is necessary: Many nuclei possess an intrinsic angular momentum, also called spin, and an associated magnetic moment μ. It is described by a spin quantum number I, which can only assume integer and half integer values and is a constant for the species of the nucleus. In the classical picture, this would mean that each nucleus of a certain species always rotates with the same, constant frequency. The 1H-nucleus, for example, has spin 1/2, while 23Na has spin 3/2 and 17O, 5/2. Other nuclei, like 12C or 16O, however, have a spin of zero, meaning that they have no angular momentum and do not precess, which makes them invisible to NMR.
Due to their magnetic moment, the nuclei with a spin larger than zero behave like tiny bar magnets. However, in the absence of an external magnetic field, this is not discernible from the outside, since their axes are arbitrarily aligned in space, all orientations having the same energy. Macroscopically, these randomly oriented magnetic moments will cancel and no effect is observed. When placed inside a magnetic field, however, the behaviour of these nuclei will change: The spins now may only assume a limited set of spin states, the number of possible states depending on the spin quantum number: A nucleus with spin I can assume (2I+1) separate states, described by numbers from −I to +I, with integer steps between the states. The 1H-nucleus can thus assume two levels, labelled −1/2 and +1/2, while 23Na can have four states between −3/2 and +3/2. Each of these states corresponds to a separate orientation of the axes of angular momentum and magnetic moment in space, described by the angle to the magnetic field direction: For 1H, the rotational axis either deflects by an angle of 54.7° from the direction of the magnetic field, or by the same angle from the opposite direction. These two different states differ in energy, an effect that is called Zeeman splitting (Fig. 2): The spins with axes oriented in direction of the field have a slightly lower energy than those pointed in the opposite direction. Although this energy difference is very small, it is the basis for all NMR experiments. If all states were populated by the same number of spins, the net effect would cancel, yielding no macroscopic magnetization. However, the small energy gap causes a tiny difference in the population numbers of the states. According to Boltzmann’s law, the population difference between two energy levels is given by:
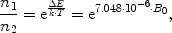
where n 1 and n 2 are the population numbers of the two states separated by the energy difference ΔE, k is Boltzmann’s constant and T is the temperature. While the left-hand part of Eq. [2] is valid for all nuclei, the number in the exponential on the right was calculated specifically for protons at room temperature.
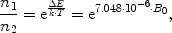
([2])

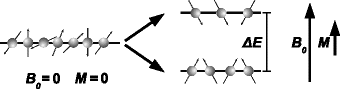
Fig. 2.
The Zeeman effect: While in absence of a magnetic field all spins have the same energy (left) and are oriented randomly, in a magnetic field the energy levels split up (right). The energy gap causes a population difference which generates a macroscopic magnetization.
Thus, the energy gap between the spin states causes slightly more spins to be oriented in the direction of the field than in the opposite one, leaving a small net effect that is used in magnetic resonance techniques. This difference is very small. For example, of one million hydrogen nuclei in a magnetic field of 3 T, only about 11 contribute to the NMR signal. This explains the limited sensitivity of NMR, which is its main drawback and poses strong constraints on the spatial resolution that can be reached in MRI experiments or on the minimum concentrations of metabolites detectable in MR spectroscopy studies.
While the magnetic moments of the individual spins thus have different orientations and behave according to the laws of quantum mechanics, the macroscopic magnetization that arises from the superposition of all the single magnetic moments is, in equilibrium, oriented parallel to the external magnetic field and behaves, under certain conditions, similar to the magnetic spinning top described in the last section. This analogy is thus often used to describe NMR experiments. However, when using this picture, keep in mind that
it describes the macroscopic magnetization and not the individual spins, which are governed by quantum mechanics,
this magnetization is much smaller than the sum of the magnetic moments of all nuclei, since it is formed only by the small surplus of nuclei in the lower energy level,
it is only valid for spins that can be assumed not to interact with any other spins. Many phenomena that play an important role in NMR experiments (e.g. spin–spin coupling or the Nuclear Overhauser effect) cannot be explained in this image. Even a thorough examination of the relaxation (which will be discussed briefly later in this section) requires quantum mechanics.
Mathematically, the motion of the magnetization in the classical picture is described by the Bloch equations, which are often used to compute the behaviour of the spins in an experiment.
2.2 Excitation
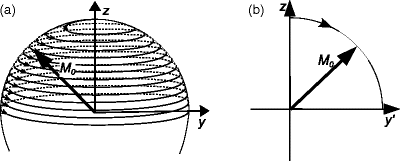
As shown above, in equilibrium, the macroscopic magnetization M 0 that is generated by the combined magnetic moments of the spinning nuclei is longitudinal, which means that it is oriented in the z-direction, parallel to the magnetic field. This corresponds to a spinning top that is standing exactly upright. It will not experience a torque and thus not precess at all. Thus, it can not be detected in an NMR experiment. To obtain a signal, the magnetization has to be forced to precess, which is, just as for the spinning top, achieved by tilting the rotational axis with respect to the external magnetic field B 0. For this, again, precession is used: Applying another external magnetic field, usually labelled B 1, perpendicular to B 0, induces an additional rotation about its direction. The magnetization will deflect from M 0 and immediately start precessing with the Larmor frequency around the direction of B 0. To obtain a steady motion away from the z-axis, the direction of this additional field has to rotate with ω 0 around the z-axis, thus following the precession of the magnetization. Only if the frequency of the second field is exactly equal to the Larmor frequency will there be an effect, which is the reason why the phenomenon is termed resonance. The necessary frequency for protons is between 63.9 MHz for 1.5 T and 1 GHz (for 23.5 T) and is thus in the radiofrequency (rf) range.
Subjected to an rf field with the correct frequency, the precession around B 0 is superimposed by a tilt towards the transverse plane (Fig. 3a). This motion is also governed by Eq. [1], though here the B 1-field determines the precession frequency:
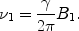
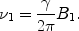
([3])

Fig. 3.
A 90° pulse in the laboratory frame (a) and in the rotating coordinate system (b). In the laboratory frame, the magnetization moves in spirals, which result as a superposition of the precession around B 0 with frequency ω 0 and that around the rotating B 1 with ω 1. In the rotating coordinate system, the B 0-field and the corresponding precession disappear, leaving just the simple rotation around the B 1-direction.
Usually, B 1 is much smaller than B 0 and ν 1 is in the order of some hundred Hertz, leading to pulse durations in the millisecond range.
If the B 1-field is turned off after time τ, the magnetization will be tilted against the z-direction by an angle 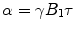 . In an NMR experiment, only the transverse component of the magnetization can be detected, which again is proportional to sin α. Maximum signal thus is obtained after a pulse with a flip angle of 90° (therefore called a 90° or a π/2 pulse) or 270°, while a 180° or 360° pulse will yield no signal at all, the magnetization being oriented towards the negative or positive z-axis, respectively.
. In an NMR experiment, only the transverse component of the magnetization can be detected, which again is proportional to sin α. Maximum signal thus is obtained after a pulse with a flip angle of 90° (therefore called a 90° or a π/2 pulse) or 270°, while a 180° or 360° pulse will yield no signal at all, the magnetization being oriented towards the negative or positive z-axis, respectively.
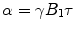 . In an NMR experiment, only the transverse component of the magnetization can be detected, which again is proportional to sin α. Maximum signal thus is obtained after a pulse with a flip angle of 90° (therefore called a 90° or a π/2 pulse) or 270°, while a 180° or 360° pulse will yield no signal at all, the magnetization being oriented towards the negative or positive z-axis, respectively.
. In an NMR experiment, only the transverse component of the magnetization can be detected, which again is proportional to sin α. Maximum signal thus is obtained after a pulse with a flip angle of 90° (therefore called a 90° or a π/2 pulse) or 270°, while a 180° or 360° pulse will yield no signal at all, the magnetization being oriented towards the negative or positive z-axis, respectively.For easier examination of the different precession components, it is practical to observe the magnetization from a rotating coordinate system. Described by coordinate axes usually labelled x ′, y ′ and z, it rotates around the z-axis with the nucleus’ resonance frequency ω 0. Now, the effect of the B 0-field is just compensated by the rotation of the coordinate system, thus eliminating the precession around the z-axis. An on-resonance rf irradiation with the Larmor frequency then corresponds to a static field perpendicular to the z-axis and thus induces a rotation around its direction with the constant frequency ν 1 (see Fig. 3b).
In the quantum mechanical interpretation of the excitation, the B 1-field induces transitions between the different spin quantum states: Electromagnetic radiation with the frequency ν carries an energy given by E = hν, h being Planck’s constant. If ν is equal to the Larmor frequency, this energy is just equal to the energy difference between the spin states. The field will thus induce transitions between the levels and cause changes in their populations.
2.3 The Free Induction Decay
The simplest NMR experiment consists of a single excitation pulse, which flips the magnetization by an angle of, e.g. 90°. It is then oriented in the transverse direction, precessing around the z-axis. The detected signal S(t) will also oscillate with ω 0 and fall off exponentially:
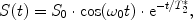
with S 0 being the initial signal amplitude and T 2 * the usual term for the decay rate, the apparent transverse relaxation time (Fig. 4). This signal is called Free Induction Decay (FID).
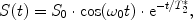
([4])

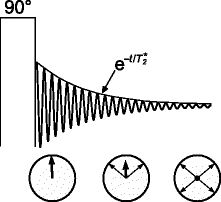
Fig. 4.




A 90° pulse flips the magnetization into the transverse plane, where it precesses. The single spins contributing to the signal have slightly different frequencies, so that their phases diverge, causing the total magnetization to decay.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree