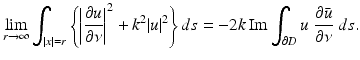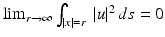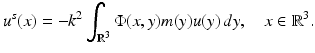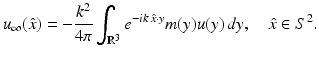(1)
for the pressure p = p(x, t), is obtained by linearization of the equations for the motion of fluids. Here, c = c(x) denotes the local speed of sound, and the fluid velocity is proportional to
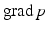 . For time-harmonic acoustic waves of the form
. For time-harmonic acoustic waves of the form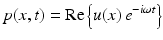
(2)
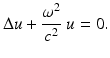
(3)
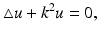
(4)
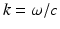 .
.A solution to the Helmholtz equation whose domain of definition contains the exterior of some sphere is called radiating if it satisfies the Sommerfeld radiation condition
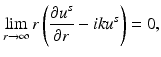
where r = | x | and the limit holds uniformly in all directions x∕ | x | . Here, and in the sequel, 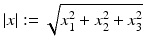 denotes the Euclidean norm of
denotes the Euclidean norm of 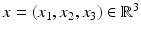 . For more details on the physical background of linear acoustic waves, the reader is referred to [66].
. For more details on the physical background of linear acoustic waves, the reader is referred to [66].
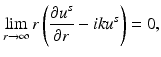
(5)
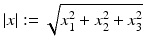 denotes the Euclidean norm of
denotes the Euclidean norm of 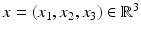 . For more details on the physical background of linear acoustic waves, the reader is referred to [66].
. For more details on the physical background of linear acoustic waves, the reader is referred to [66].We will confine our presentation of scattering theory for time-harmonic acoustic waves to two basic problems, namely, scattering by a bounded impenetrable obstacle and scattering by a penetrable inhomogeneous medium of compact support. For a vector 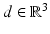 with | d | = 1, the function e ik x⋅ d satisfies the Helmholtz equation for all
with | d | = 1, the function e ik x⋅ d satisfies the Helmholtz equation for all 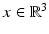 . It is called a plane wave, since e i(k x⋅ d−ω t) is constant on the planes
. It is called a plane wave, since e i(k x⋅ d−ω t) is constant on the planes 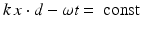 . Note that these wave fronts travel with velocity c in the direction d. Assume that an incident field is given by the plane wave u i (x) = e ik x⋅ d . Then the simplest obstacle scattering problem is to find the scattered field u s as a radiating solution to the Helmholtz equation in the exterior of a bounded scatterer D such that the total field
. Note that these wave fronts travel with velocity c in the direction d. Assume that an incident field is given by the plane wave u i (x) = e ik x⋅ d . Then the simplest obstacle scattering problem is to find the scattered field u s as a radiating solution to the Helmholtz equation in the exterior of a bounded scatterer D such that the total field 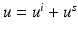 satisfies the Dirichlet boundary condition
satisfies the Dirichlet boundary condition
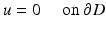
corresponding to a sound-soft obstacle with the total pressure, i.e., the excess pressure over the static pressure p 0, vanishing on the boundary. Concerning the geometry of scattering obstacles, for simplicity, we always will assume that D is a bounded domain with a connected boundary ∂ D of class C 2. In particular, this implies that the complement 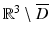 is connected. However, our results remain valid for a finite number of scattering obstacles.
is connected. However, our results remain valid for a finite number of scattering obstacles.
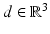 with | d | = 1, the function e ik x⋅ d satisfies the Helmholtz equation for all
with | d | = 1, the function e ik x⋅ d satisfies the Helmholtz equation for all 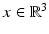 . It is called a plane wave, since e i(k x⋅ d−ω t) is constant on the planes
. It is called a plane wave, since e i(k x⋅ d−ω t) is constant on the planes 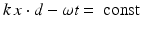 . Note that these wave fronts travel with velocity c in the direction d. Assume that an incident field is given by the plane wave u i (x) = e ik x⋅ d . Then the simplest obstacle scattering problem is to find the scattered field u s as a radiating solution to the Helmholtz equation in the exterior of a bounded scatterer D such that the total field
. Note that these wave fronts travel with velocity c in the direction d. Assume that an incident field is given by the plane wave u i (x) = e ik x⋅ d . Then the simplest obstacle scattering problem is to find the scattered field u s as a radiating solution to the Helmholtz equation in the exterior of a bounded scatterer D such that the total field 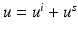 satisfies the Dirichlet boundary condition
satisfies the Dirichlet boundary condition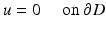
(6)
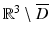 is connected. However, our results remain valid for a finite number of scattering obstacles.
is connected. However, our results remain valid for a finite number of scattering obstacles.Boundary conditions other than the Dirichlet condition also need to be considered such as the Neumann or sound-hard boundary condition
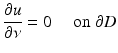
or, more generally, the impedance boundary condition
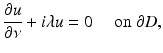
where ν is the outward unit normal to ∂ D and λ is a positive constant called the surface impedance. More generally the impedance λ can also vary on ∂ D. Since 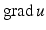 is proportional to the fluid velocity, the impedance boundary condition describes obstacles for which the normal velocity of the fluid on the boundary is proportional to the excess pressure on the boundary. The Neumann condition corresponds to a vanishing normal velocity on the boundary. In order to avoid repetitions by considering all possible types of boundary conditions, we will in general confine ourselves to presenting the basic ideas in acoustic obstacle scattering for the case of a sound-soft obstacle.
is proportional to the fluid velocity, the impedance boundary condition describes obstacles for which the normal velocity of the fluid on the boundary is proportional to the excess pressure on the boundary. The Neumann condition corresponds to a vanishing normal velocity on the boundary. In order to avoid repetitions by considering all possible types of boundary conditions, we will in general confine ourselves to presenting the basic ideas in acoustic obstacle scattering for the case of a sound-soft obstacle.
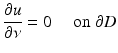
(7)
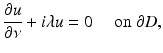
(8)
 is proportional to the fluid velocity, the impedance boundary condition describes obstacles for which the normal velocity of the fluid on the boundary is proportional to the excess pressure on the boundary. The Neumann condition corresponds to a vanishing normal velocity on the boundary. In order to avoid repetitions by considering all possible types of boundary conditions, we will in general confine ourselves to presenting the basic ideas in acoustic obstacle scattering for the case of a sound-soft obstacle.
is proportional to the fluid velocity, the impedance boundary condition describes obstacles for which the normal velocity of the fluid on the boundary is proportional to the excess pressure on the boundary. The Neumann condition corresponds to a vanishing normal velocity on the boundary. In order to avoid repetitions by considering all possible types of boundary conditions, we will in general confine ourselves to presenting the basic ideas in acoustic obstacle scattering for the case of a sound-soft obstacle.The simplest scattering problem for an inhomogeneous medium assumes that the speed of sound is constant outside a bounded domain D. Then the total field 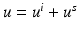 satisfies
satisfies
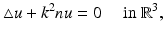
and the scattered wave u s fulfills the Sommerfeld radiation condition (5), where the wave number is given by 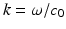 and
and 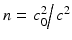 is the refractive index given by the ratio of the square of the sound speeds c = c 0 in the homogeneous host medium and c = c(x) in the inhomogeneous medium. The refractive index is positive and satisfies n(x) = 1 for x ∉ D, and we assume n to be continuously differentiable in
is the refractive index given by the ratio of the square of the sound speeds c = c 0 in the homogeneous host medium and c = c(x) in the inhomogeneous medium. The refractive index is positive and satisfies n(x) = 1 for x ∉ D, and we assume n to be continuously differentiable in  (our results are also in general valid for n being merely piecewise continuous in
(our results are also in general valid for n being merely piecewise continuous in  ). An absorbing medium is modeled by adding an absorption term which leads to a refractive index with a positive imaginary part of the form
). An absorbing medium is modeled by adding an absorption term which leads to a refractive index with a positive imaginary part of the form
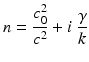 in terms of a possibly space-dependent absorption coefficient γ.
in terms of a possibly space-dependent absorption coefficient γ.
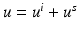 satisfies
satisfies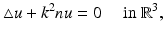
(9)
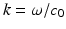 and
and 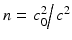 is the refractive index given by the ratio of the square of the sound speeds c = c 0 in the homogeneous host medium and c = c(x) in the inhomogeneous medium. The refractive index is positive and satisfies n(x) = 1 for x ∉ D, and we assume n to be continuously differentiable in
is the refractive index given by the ratio of the square of the sound speeds c = c 0 in the homogeneous host medium and c = c(x) in the inhomogeneous medium. The refractive index is positive and satisfies n(x) = 1 for x ∉ D, and we assume n to be continuously differentiable in 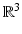 (our results are also in general valid for n being merely piecewise continuous in
(our results are also in general valid for n being merely piecewise continuous in 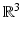 ). An absorbing medium is modeled by adding an absorption term which leads to a refractive index with a positive imaginary part of the form
). An absorbing medium is modeled by adding an absorption term which leads to a refractive index with a positive imaginary part of the form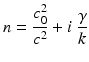
Summarizing, given the incident wave and the physical properties of the scatterer, the direct scattering problem is to find the scattered wave and in particular its behavior at large distances from the scattering object, i.e., its far-field behavior. The inverse scattering problem takes this answer to the direct scattering problem as its starting point and asks what the nature of the scatterer that gave rise to such far-field behavior is.
To be more specific, it can be shown that radiating solutions u s to the Helmholtz equation have the asymptotic behavior
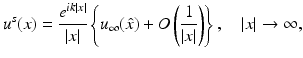
uniformly for all directions 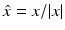 , where the function u ∞ defined on the unit sphere S 2 is known as the far-field pattern of the scattered wave. For plane wave incidence, we indicate the dependence of the far-field pattern on the incident direction d and the observation direction
, where the function u ∞ defined on the unit sphere S 2 is known as the far-field pattern of the scattered wave. For plane wave incidence, we indicate the dependence of the far-field pattern on the incident direction d and the observation direction 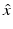 by writing
by writing 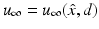 . The inverse scattering problem can now be formulated as the problem of determining either the sound-soft obstacle D or the index of refraction n (and hence also D) from a knowledge of the far-field pattern
. The inverse scattering problem can now be formulated as the problem of determining either the sound-soft obstacle D or the index of refraction n (and hence also D) from a knowledge of the far-field pattern 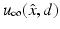 for
for 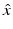 and d on the unit sphere S 2 (or a subset of S 2).
and d on the unit sphere S 2 (or a subset of S 2).
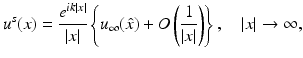
(10)
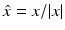 , where the function u ∞ defined on the unit sphere S 2 is known as the far-field pattern of the scattered wave. For plane wave incidence, we indicate the dependence of the far-field pattern on the incident direction d and the observation direction
, where the function u ∞ defined on the unit sphere S 2 is known as the far-field pattern of the scattered wave. For plane wave incidence, we indicate the dependence of the far-field pattern on the incident direction d and the observation direction 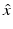 by writing
by writing 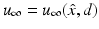 . The inverse scattering problem can now be formulated as the problem of determining either the sound-soft obstacle D or the index of refraction n (and hence also D) from a knowledge of the far-field pattern
. The inverse scattering problem can now be formulated as the problem of determining either the sound-soft obstacle D or the index of refraction n (and hence also D) from a knowledge of the far-field pattern 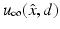 for
for 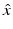 and d on the unit sphere S 2 (or a subset of S 2).
and d on the unit sphere S 2 (or a subset of S 2).One of the earliest mathematical results in inverse scattering theory was Schiffer’s proof in 1967 that the far-field pattern 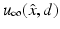 for
for 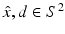 uniquely determines the shape of a sound-soft obstacle D. Unfortunately, Schiffer’s proof does not immediately generalize to other boundary conditions. This problem was remedied by Kirsch and Kress in 1993 who, using an idea originally proposed by Isakov, showed that
uniquely determines the shape of a sound-soft obstacle D. Unfortunately, Schiffer’s proof does not immediately generalize to other boundary conditions. This problem was remedied by Kirsch and Kress in 1993 who, using an idea originally proposed by Isakov, showed that 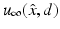 for
for 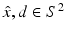 uniquely determines the shape of D as long as the solution of the direct scattering problem depends continuously on the boundary data [54]. In particular, it is not necessary to know the boundary condition a priori in order to guarantee uniqueness! The uniqueness problem for inverse scattering by an inhomogeneous medium was solved by Nachman [68], Novikov [70], and Ramm [79] in 1988 who based their analysis on the fundamental work of Sylvester and Uhlmann [88]. Their uniqueness proof was subsequently considerably simplified by Hähner [35].
uniquely determines the shape of D as long as the solution of the direct scattering problem depends continuously on the boundary data [54]. In particular, it is not necessary to know the boundary condition a priori in order to guarantee uniqueness! The uniqueness problem for inverse scattering by an inhomogeneous medium was solved by Nachman [68], Novikov [70], and Ramm [79] in 1988 who based their analysis on the fundamental work of Sylvester and Uhlmann [88]. Their uniqueness proof was subsequently considerably simplified by Hähner [35].
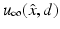 for
for 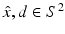 uniquely determines the shape of a sound-soft obstacle D. Unfortunately, Schiffer’s proof does not immediately generalize to other boundary conditions. This problem was remedied by Kirsch and Kress in 1993 who, using an idea originally proposed by Isakov, showed that
uniquely determines the shape of a sound-soft obstacle D. Unfortunately, Schiffer’s proof does not immediately generalize to other boundary conditions. This problem was remedied by Kirsch and Kress in 1993 who, using an idea originally proposed by Isakov, showed that 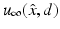 for
for 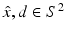 uniquely determines the shape of D as long as the solution of the direct scattering problem depends continuously on the boundary data [54]. In particular, it is not necessary to know the boundary condition a priori in order to guarantee uniqueness! The uniqueness problem for inverse scattering by an inhomogeneous medium was solved by Nachman [68], Novikov [70], and Ramm [79] in 1988 who based their analysis on the fundamental work of Sylvester and Uhlmann [88]. Their uniqueness proof was subsequently considerably simplified by Hähner [35].
uniquely determines the shape of D as long as the solution of the direct scattering problem depends continuously on the boundary data [54]. In particular, it is not necessary to know the boundary condition a priori in order to guarantee uniqueness! The uniqueness problem for inverse scattering by an inhomogeneous medium was solved by Nachman [68], Novikov [70], and Ramm [79] in 1988 who based their analysis on the fundamental work of Sylvester and Uhlmann [88]. Their uniqueness proof was subsequently considerably simplified by Hähner [35].The first attempt to reconstruct the shape of a sound-soft scattering obstacle from a knowledge of the far-field pattern in a manner acknowledging the nonlinear and ill-posed nature of the problem was made by Roger in 1981 using Newton’s iteration method [81]. A characterization and rigorous proof of the existence of the Fréchet derivative of the solution operator in Newton’s method were then established by Kirsch [47] and Potthast [75] in 1993 and 1994, respectively. An alternative approach to solving the inverse scattering problem was proposed by Colton and Monk in 1986 and by Kirsch and Kress in 1987 who broke up the inverse scattering problem into a linear, ill-posed problem and a nonlinear, well-posed problem [24, 53]. The optimization method of Kirsch and Kress has the attractive feature of needing only a single incident field for its implementation. On the other hand, to use such methods, it is necessary to know the number of components of the scatterer as well as the boundary condition satisfied by the field on the surface of the scatterer. These problems were overcome by Colton and Kirsch in 1996 through the derivation of a linear integral equation with the far-field data as its kernel (i.e., multistatic data is needed for its implementation) [19]. This method, subsequently called the linear sampling method , was further developed by Colton et al. [29] and numerous other researchers. A significant development in this approach to the inverse scattering problem was the introduction of the factorization method by Kirsch in 1998 [48]. For further historical information on these “sampling” methods in inverse scattering theory, we refer the reader to the chapter in this handbook on sampling methods as well as the monographs [7, 52].
Optimization methods and sampling methods for the inverse scattering problem for inhomogeneous media have been extensively investigated by numerous authors. In general, the optimization methods are based on rewriting the scattering problem corresponding to (9) as the Lippmann–Schwinger integral equation
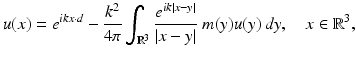
where 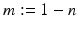 and the object is to determine m from a knowledge of
and the object is to determine m from a knowledge of
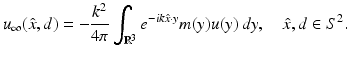
On the other hand, sampling methods have also been used to study the inverse scattering problem associated with (9) where now the object is to only determine the support of m. For details and further references, see [7, 22, 52].
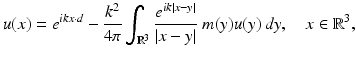
(11)
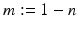 and the object is to determine m from a knowledge of
and the object is to determine m from a knowledge of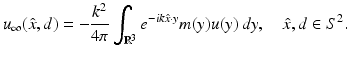
(12)
Finally, as pointed out in [21], an alternative direction in inverse scattering theory than that discussed above is to only try to obtain lower and upper bounds on a few relevant features of the scattering object rather than attempting a complete reconstruction. This relatively new direction in inverse scattering theory will be discussed in Sect. 5.
2 Direct Scattering Problems
The Helmholtz Equation
Most of the basic properties of solutions to the Helmholtz equation (3) can be deduced from the fundamental solution
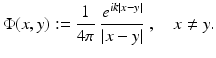
For fixed 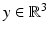 , it satisfies the Helmholtz equation in
, it satisfies the Helmholtz equation in 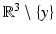 . In addition, it satisfies the radiation condition (5) uniformly with respect to y on compact subsets of
. In addition, it satisfies the radiation condition (5) uniformly with respect to y on compact subsets of 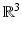 . Physically speaking, the fundamental solution represents an acoustic point source located at the point y. In addition to plane waves, point sources will also occur as incident fields in scattering problems.
. Physically speaking, the fundamental solution represents an acoustic point source located at the point y. In addition to plane waves, point sources will also occur as incident fields in scattering problems.
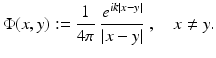
(13)
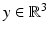 , it satisfies the Helmholtz equation in
, it satisfies the Helmholtz equation in 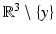 . In addition, it satisfies the radiation condition (5) uniformly with respect to y on compact subsets of
. In addition, it satisfies the radiation condition (5) uniformly with respect to y on compact subsets of 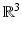 . Physically speaking, the fundamental solution represents an acoustic point source located at the point y. In addition to plane waves, point sources will also occur as incident fields in scattering problems.
. Physically speaking, the fundamental solution represents an acoustic point source located at the point y. In addition to plane waves, point sources will also occur as incident fields in scattering problems.Green’s integral theorems provide basic tools for investigating the Helmholtz equation. As an immediate consequence, they imply the Helmholtz representation
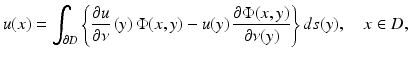
for solutions 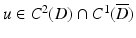 to the Helmholtz equation. The representation (2) implies that solutions to the Helmholtz equation inherit analyticity from the fundamental solution. Any solution u to the Helmholtz equation in D satisfying
to the Helmholtz equation. The representation (2) implies that solutions to the Helmholtz equation inherit analyticity from the fundamental solution. Any solution u to the Helmholtz equation in D satisfying
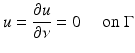
for some open subset 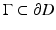 must vanish identically in D. This can be seen via extending the definition of u by (2) for
must vanish identically in D. This can be seen via extending the definition of u by (2) for 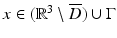 . Then, by Green’s integral theorem, applied to u and
. Then, by Green’s integral theorem, applied to u and 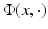 , we have u = 0 in
, we have u = 0 in 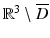 . Clearly u solves the Helmholtz equation in
. Clearly u solves the Helmholtz equation in 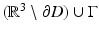 and therefore by analyticity u = 0 in D since D and
and therefore by analyticity u = 0 in D since D and 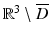 are connected through the gap
are connected through the gap 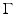 in ∂ D.
in ∂ D.
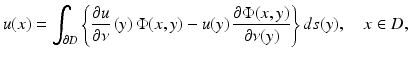
(14)
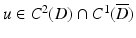 to the Helmholtz equation. The representation (2) implies that solutions to the Helmholtz equation inherit analyticity from the fundamental solution. Any solution u to the Helmholtz equation in D satisfying
to the Helmholtz equation. The representation (2) implies that solutions to the Helmholtz equation inherit analyticity from the fundamental solution. Any solution u to the Helmholtz equation in D satisfying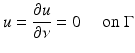
(15)
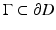 must vanish identically in D. This can be seen via extending the definition of u by (2) for
must vanish identically in D. This can be seen via extending the definition of u by (2) for 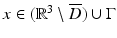 . Then, by Green’s integral theorem, applied to u and
. Then, by Green’s integral theorem, applied to u and 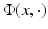 , we have u = 0 in
, we have u = 0 in 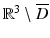 . Clearly u solves the Helmholtz equation in
. Clearly u solves the Helmholtz equation in 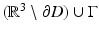 and therefore by analyticity u = 0 in D since D and
and therefore by analyticity u = 0 in D since D and 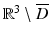 are connected through the gap
are connected through the gap 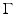 in ∂ D.
in ∂ D.As a consequence of the radiation condition (5), the Helmholtz representation is also valid in the exterior domain 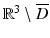 , i.e., we have
, i.e., we have
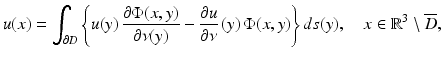
for radiating solutions 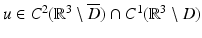 to the Helmholtz equation. From Eq. (4) we observe that radiating solutions u to the Helmholtz equation satisfy Sommerfeld’s finiteness condition
to the Helmholtz equation. From Eq. (4) we observe that radiating solutions u to the Helmholtz equation satisfy Sommerfeld’s finiteness condition
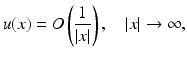
uniformly for all directions and that the validity of the Sommerfeld radiation condition (5) is invariant under translations of the origin.
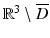 , i.e., we have
, i.e., we have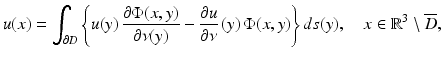
(16)
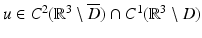 to the Helmholtz equation. From Eq. (4) we observe that radiating solutions u to the Helmholtz equation satisfy Sommerfeld’s finiteness condition
to the Helmholtz equation. From Eq. (4) we observe that radiating solutions u to the Helmholtz equation satisfy Sommerfeld’s finiteness condition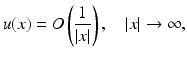
(17)
We are now in a position to introduce the fundamental notion of the far-field pattern of radiating solutions to the Helmholtz equation.
Theorem 1.
Every radiating solution u to the Helmholtz equation has an asymptotic behavior of the form
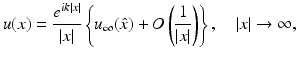
uniformly in all directions 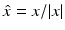 , where the function u ∞ defined on the unit sphere S 2 is called the far-field pattern of u. Under the assumptions of (16), we have
, where the function u ∞ defined on the unit sphere S 2 is called the far-field pattern of u. Under the assumptions of (16), we have
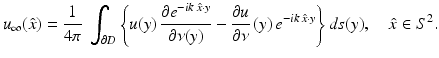
(18)
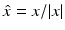 , where the function u ∞ defined on the unit sphere S 2 is called the far-field pattern of u. Under the assumptions of (16), we have
, where the function u ∞ defined on the unit sphere S 2 is called the far-field pattern of u. Under the assumptions of (16), we have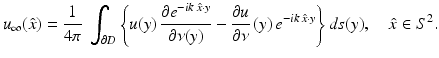
(19)
Proof.
This follows from (16) by using the estimates
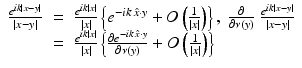 which hold uniformly for all y ∈ ∂ D and all directions x∕ | x | as | x | → ∞. ■
which hold uniformly for all y ∈ ∂ D and all directions x∕ | x | as | x | → ∞. ■
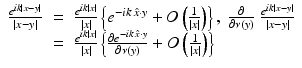
From the representation (19), it follows that the far-field pattern is an analytic function on S 2. As an extension of (18), each radiating solution u to the Helmholtz equation has an Atkinson–Wilcox expansion of the form
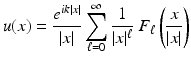
that converges absolutely and uniformly on compact subsets of  , where
, where 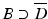 is a ball centered at the origin. The coefficients in the expansion (20) are determined in terms of the far-field pattern F 0 = u ∞ by the recursion
is a ball centered at the origin. The coefficients in the expansion (20) are determined in terms of the far-field pattern F 0 = u ∞ by the recursion
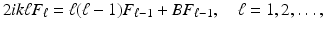
where B denotes the Laplace–Beltrami operator for the unit sphere. The following consequence of the expansion (20) is known as Rellich’s lemma .
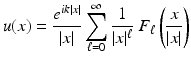
(20)
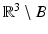 , where
, where 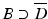 is a ball centered at the origin. The coefficients in the expansion (20) are determined in terms of the far-field pattern F 0 = u ∞ by the recursion
is a ball centered at the origin. The coefficients in the expansion (20) are determined in terms of the far-field pattern F 0 = u ∞ by the recursion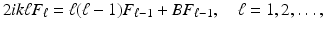
(21)
Lemma 1.
Let u be a radiating solution to the Helmholtz equation for which the far-field pattern u ∞ vanishes identically. Then u vanishes identically.
Proof.
Corollary 1.
Let 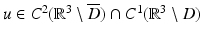 be a radiating solution to the Helmholtz equation in
be a radiating solution to the Helmholtz equation in 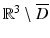 for which
for which
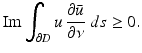
Then u = 0 in 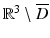 .
.
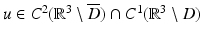 be a radiating solution to the Helmholtz equation in
be a radiating solution to the Helmholtz equation in 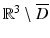 for which
for which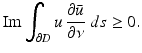
(22)
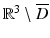 .
.Proof.
Scattering from infinitely long cylindrical obstacles or inhomogeneities leads to the Helmholtz equation in 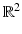 . The two-dimensional case can be used as an approximation for scattering from finitely long cylinders, and more importantly, it can serve as a model case for testing numerical approximation schemes in direct and inverse scattering. Without giving details, we can summarize that our analysis remains valid in two dimensions after appropriate modifications of the fundamental solution and the radiation condition. The fundamental solution to the Helmholtz equation in two dimensions is given by
. The two-dimensional case can be used as an approximation for scattering from finitely long cylinders, and more importantly, it can serve as a model case for testing numerical approximation schemes in direct and inverse scattering. Without giving details, we can summarize that our analysis remains valid in two dimensions after appropriate modifications of the fundamental solution and the radiation condition. The fundamental solution to the Helmholtz equation in two dimensions is given by
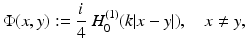
in terms of the Hankel function H 0 (1) of the first kind of order zero. In 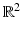 the Sommerfeld radiation condition has to be replaced by
the Sommerfeld radiation condition has to be replaced by
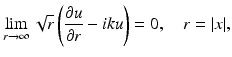
uniformly for all directions x∕ | x | . According to the form (24) of the radiation condition, the definition of the far-field pattern (18) has to be replaced by
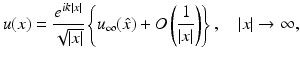
and the representation (19) assumes the form
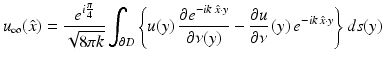
for 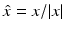 .
.
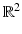 . The two-dimensional case can be used as an approximation for scattering from finitely long cylinders, and more importantly, it can serve as a model case for testing numerical approximation schemes in direct and inverse scattering. Without giving details, we can summarize that our analysis remains valid in two dimensions after appropriate modifications of the fundamental solution and the radiation condition. The fundamental solution to the Helmholtz equation in two dimensions is given by
. The two-dimensional case can be used as an approximation for scattering from finitely long cylinders, and more importantly, it can serve as a model case for testing numerical approximation schemes in direct and inverse scattering. Without giving details, we can summarize that our analysis remains valid in two dimensions after appropriate modifications of the fundamental solution and the radiation condition. The fundamental solution to the Helmholtz equation in two dimensions is given by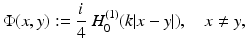
(23)
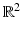 the Sommerfeld radiation condition has to be replaced by
the Sommerfeld radiation condition has to be replaced by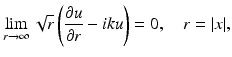
(24)
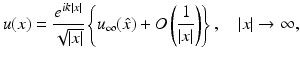
(25)
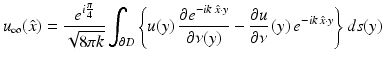
(26)
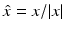 .
. Obstacle Scattering
After renaming the unknown functions, the direct scattering problem for sound-soft obstacles is a special case of the following exterior Dirichlet problem: Given a function f ∈ C(∂ D), find a radiating solution 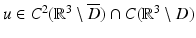 to the Helmholtz equation that satisfies the boundary condition
to the Helmholtz equation that satisfies the boundary condition
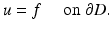
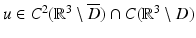 to the Helmholtz equation that satisfies the boundary condition
to the Helmholtz equation that satisfies the boundary condition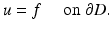
(27)
Theorem 2.
The exterior Dirichlet problem for the Helmholtz equation has at most one solution.
Proof.
Let u satisfy the homogeneous boundary condition u = 0 on ∂ D. If u were continuously differentiable up to the boundary, we could immediately apply Corollary 1 to obtain u = 0 in 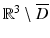 . However, in the formulation of the exterior Dirichlet problem,
. However, in the formulation of the exterior Dirichlet problem, 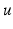 is only assumed to be in
is only assumed to be in 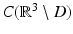 . We refrain from discussing possibilities to overcome this regularity gap and refer to the literature [22]. ■
. We refrain from discussing possibilities to overcome this regularity gap and refer to the literature [22]. ■
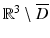 . However, in the formulation of the exterior Dirichlet problem,
. However, in the formulation of the exterior Dirichlet problem, 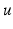 is only assumed to be in
is only assumed to be in 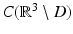 . We refrain from discussing possibilities to overcome this regularity gap and refer to the literature [22]. ■
. We refrain from discussing possibilities to overcome this regularity gap and refer to the literature [22]. ■ Theorem 3.
The exterior Dirichlet problem has a unique solution.
Proof.
The existence of a solution can be elegantly based on boundary integral equations. In the layer approach, one tries to find the solution in the form of a combined acoustic double- and single-layer potential
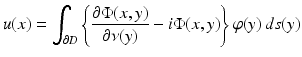
for 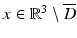 with a density
with a density 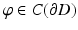 . Then, after introducing the single- and double-layer integral operators S, K: C(∂ D) → C(∂ D) by
. Then, after introducing the single- and double-layer integral operators S, K: C(∂ D) → C(∂ D) by
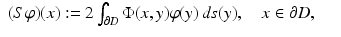
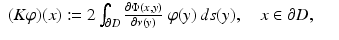
and using their regularity and jump relations, it can be seen that (28) solves the exterior Dirichlet problem provided the density φ is a solution of the integral equation
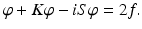
Due to their weakly singular kernels, the operators S and K turn out to be compact. Hence, the existence of a solution to (31) can be established with the aid of the Riesz–Fredholm theory for compact operators by showing that the homogeneous form of (31) only allows the trivial solution φ = 0.
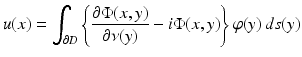
(28)
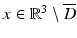 with a density
with a density 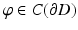 . Then, after introducing the single- and double-layer integral operators S, K: C(∂ D) → C(∂ D) by
. Then, after introducing the single- and double-layer integral operators S, K: C(∂ D) → C(∂ D) by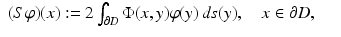
(29)
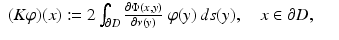
(30)
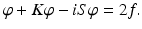
(31)
Let φ be a solution of the homogeneous equation, and let the subscripts ± denote the limits obtained by approaching ∂ D from 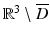 and D, respectively. Then the potential u defined by (28) in all of
and D, respectively. Then the potential u defined by (28) in all of 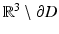 satisfies the homogeneous boundary condition
satisfies the homogeneous boundary condition 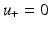 on ∂ D whence u = 0 in
on ∂ D whence u = 0 in 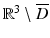 followed by Theorem 2. The jump relations for single- and double-layer potentials now yield
followed by Theorem 2. The jump relations for single- and double-layer potentials now yield
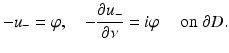 Hence, using Green’s first integral theorem, we obtain
Hence, using Green’s first integral theorem, we obtain
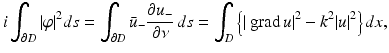 and taking the imaginary part yields φ = 0. ■
and taking the imaginary part yields φ = 0. ■
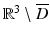 and D, respectively. Then the potential u defined by (28) in all of
and D, respectively. Then the potential u defined by (28) in all of 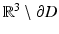 satisfies the homogeneous boundary condition
satisfies the homogeneous boundary condition 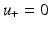 on ∂ D whence u = 0 in
on ∂ D whence u = 0 in 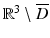 followed by Theorem 2. The jump relations for single- and double-layer potentials now yield
followed by Theorem 2. The jump relations for single- and double-layer potentials now yield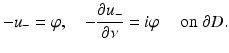
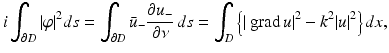
We note that, in addition to existence of a solution, the Riesz–Fredholm theory also establishes well-posedness, i.e., the continuous dependence of the solution on the data. Instead of the classical setting of continuous function spaces, the existence analysis can also be considered in the Sobolev space H 1∕2(∂ D) for the boundary integral operators leading to solutions in the energy space 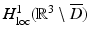 (see [64, 69]).
(see [64, 69]).
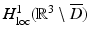 (see [64, 69]).
(see [64, 69]).We further note that without the single-layer potential included in (28), the corresponding double-layer integral equation suffers from nonuniqueness if k is a so-called irregular wave number or internal resonance, i.e., if there exist nontrivial solutions u to the Helmholtz equation in the interior domain D satisfying homogeneous Neumann boundary conditions 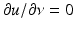 on ∂ D.
on ∂ D.
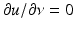 on ∂ D.
on ∂ D.For the numerical solution of the boundary integral equations in scattering theory via spectral methods in two and three dimensions, we refer to [22]. For boundary element methods, we refer to [80].
In general, for the scattering problem, the boundary values are as smooth as the boundary, since they are given by the restriction of the analytic function u i to ∂ D. Therefore, we may use the Helmholtz representation (16) and Green’s second integral theorem applied to u i and 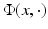 to obtain the following theorem.
to obtain the following theorem.
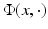 to obtain the following theorem.
to obtain the following theorem.Theorem 4.
For scattering from a sound-soft obstacle D, we have
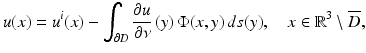
and the far-field pattern of the scattered field u s is given by
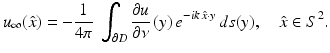
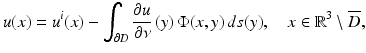
(32)
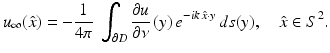
(33)
The representation (32) for the scattered field through the so-called secondary sources on the boundary is known as Huygens’ principle . Here we will use it for the motivation of the Kirchhoff or physical optics approximation as an intuitive procedure to simplify the direct scattering problem. For large wave numbers k, i.e., for small wave lengths, in a first approximation, a convex object D locally may be considered at each point x of ∂ D as a plane with normal ν(x). This suggests
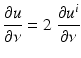 on the part
on the part 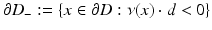 that is illuminated and
that is illuminated and
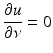 in the shadow region
in the shadow region 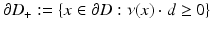 . Thus, the Kirchhoff approximation for the scattering of a plane wave with incident direction d at a convex sound-soft obstacle is given by
. Thus, the Kirchhoff approximation for the scattering of a plane wave with incident direction d at a convex sound-soft obstacle is given by
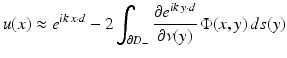
for 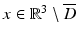 .
.
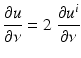
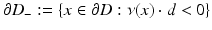 that is illuminated and
that is illuminated and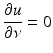
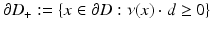 . Thus, the Kirchhoff approximation for the scattering of a plane wave with incident direction d at a convex sound-soft obstacle is given by
. Thus, the Kirchhoff approximation for the scattering of a plane wave with incident direction d at a convex sound-soft obstacle is given by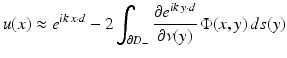
(34)
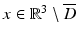 .
. Scattering by an Inhomogeneous Medium
Recall the scattering problem for an inhomogeneous medium with refractive index n as described by (9) for the total wave 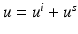 with incident field u i and the scattered wave u s satisfying the Sommerfeld radiation condition. The function
with incident field u i and the scattered wave u s satisfying the Sommerfeld radiation condition. The function 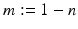 has support
has support 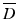 .
.
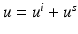 with incident field u i and the scattered wave u s satisfying the Sommerfeld radiation condition. The function
with incident field u i and the scattered wave u s satisfying the Sommerfeld radiation condition. The function 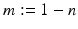 has support
has support 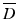 .
.The counterpart of the Helmholtz representation is given by the Lippmann–Schwinger equation
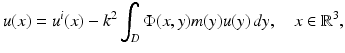
which can be shown to be equivalent to the scattering problem.
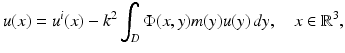
(35)
In order to establish existence of a solution to (35) via the Riesz–Fredholm theory, it must be shown that the homogeneous equation has only the trivial solution or, equivalently, that the only solution to (9) satisfying the radiation condition is identically zero. For this, in addition to Rellich’s lemma, the following unique continuation principle is required: Any solution u ∈ C 2(G) of Eq. (9) in a domain 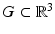 such that n ∈ C(G) and u vanishes in an open subset of G vanishes identically. Hence, we have the following result on existence and uniqueness for the inhomogeneous medium scattering problem.
such that n ∈ C(G) and u vanishes in an open subset of G vanishes identically. Hence, we have the following result on existence and uniqueness for the inhomogeneous medium scattering problem.
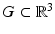 such that n ∈ C(G) and u vanishes in an open subset of G vanishes identically. Hence, we have the following result on existence and uniqueness for the inhomogeneous medium scattering problem.
such that n ∈ C(G) and u vanishes in an open subset of G vanishes identically. Hence, we have the following result on existence and uniqueness for the inhomogeneous medium scattering problem.Theorem 5.
For a refractive index 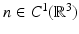 with
with 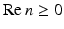 and
and 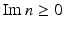 , the Lippmann–Schwinger equation or, equivalently, the inhomogeneous medium scattering problem has a unique solution.
, the Lippmann–Schwinger equation or, equivalently, the inhomogeneous medium scattering problem has a unique solution.
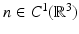 with
with 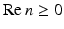 and
and 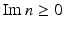 , the Lippmann–Schwinger equation or, equivalently, the inhomogeneous medium scattering problem has a unique solution.
, the Lippmann–Schwinger equation or, equivalently, the inhomogeneous medium scattering problem has a unique solution. Proof.
From Green’s first integral theorem, it follows that
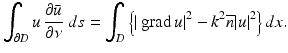 Taking the imaginary part and applying Corollary 1 yields u = 0 in
Taking the imaginary part and applying Corollary 1 yields u = 0 in  in view of the assumptions on n, and the proof is finished by the unique continuation principle. ■
in view of the assumptions on n, and the proof is finished by the unique continuation principle. ■
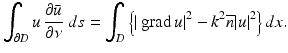
 in view of the assumptions on n, and the proof is finished by the unique continuation principle. ■
in view of the assumptions on n, and the proof is finished by the unique continuation principle. ■ We note that for 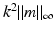 sufficiently small, u can be obtained by the method of successive approximations. If in (36) we replace u by the first term in this iterative process, we obtain the Born approximation
sufficiently small, u can be obtained by the method of successive approximations. If in (36) we replace u by the first term in this iterative process, we obtain the Born approximation
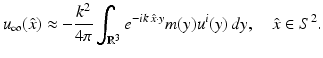
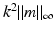 sufficiently small, u can be obtained by the method of successive approximations. If in (36) we replace u by the first term in this iterative process, we obtain the Born approximation
sufficiently small, u can be obtained by the method of successive approximations. If in (36) we replace u by the first term in this iterative process, we obtain the Born approximation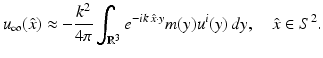
(37)
For numerical solutions of the inverse medium scattering problem by finite element methods coupled with boundary element methods via nonlocal boundary conditions, we refer to [65].
The Maxwell Equations
We now consider the Maxwell equations as the foundation of electromagnetic scattering theory. Our presentation is organized parallel to that on the Helmholtz equation, i.e., on acoustic scattering, and will be confined to homogeneous isotropic media. Consider electromagnetic wave propagation in an isotropic dielectric medium in 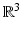 with constant electric permittivity
with constant electric permittivity 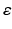 and magnetic permeability μ. The electromagnetic wave is described by the electric field
and magnetic permeability μ. The electromagnetic wave is described by the electric field 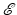 and the magnetic field
and the magnetic field 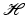 satisfying the time-dependent Maxwell equations
satisfying the time-dependent Maxwell equations
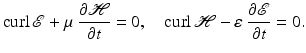
For time-harmonic electromagnetic waves of the form
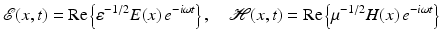
with frequency ω > 0, the complex-valued space-dependent parts E and H satisfy the reduced Maxwell equations
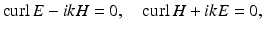
where the wave number k is given by the positive constant 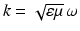 . We will only be concerned with the reduced Maxwell equations and will henceforth refer to them as the Maxwell equations.
. We will only be concerned with the reduced Maxwell equations and will henceforth refer to them as the Maxwell equations.
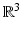 with constant electric permittivity
with constant electric permittivity 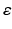 and magnetic permeability μ. The electromagnetic wave is described by the electric field
and magnetic permeability μ. The electromagnetic wave is described by the electric field 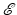 and the magnetic field
and the magnetic field 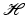 satisfying the time-dependent Maxwell equations
satisfying the time-dependent Maxwell equations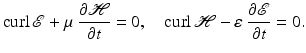
(38)
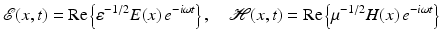
(39)
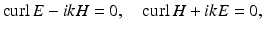
(40)
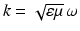 . We will only be concerned with the reduced Maxwell equations and will henceforth refer to them as the Maxwell equations.
. We will only be concerned with the reduced Maxwell equations and will henceforth refer to them as the Maxwell equations.A solution E, H to the Maxwell equations whose domain of definition contains the exterior of some sphere is called radiating if it satisfies one of the Silver–Müller radiation conditions
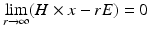
or
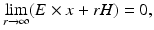
where r = | x | and the limits hold uniformly in all directions x∕ | x | . For more details on the physical background of electromagnetic waves, we refer to [46, 67].
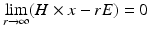
(41)
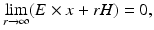
(42)
For the Maxwell equations, the counterpart of the Helmholtz representation (2) is given by the Stratton–Chu formula
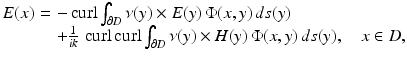
for solutions 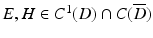 to the Maxwell equations. A corresponding representation for H can be obtained from (43) with the aid of
to the Maxwell equations. A corresponding representation for H can be obtained from (43) with the aid of 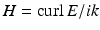 .
.
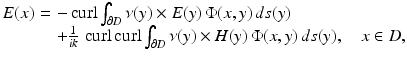
(43)
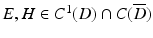 to the Maxwell equations. A corresponding representation for H can be obtained from (43) with the aid of
to the Maxwell equations. A corresponding representation for H can be obtained from (43) with the aid of 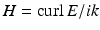 .
.The representation (43) implies that each continuously differentiable solution to the Maxwell equations automatically has analytic Cartesian components. Therefore, one can employ the vector identity 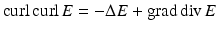 to prove that for a solution E, H to the Maxwell equations, both E and H are divergence-free and satisfy the vector Helmholtz equation. Conversely, if E is a solution to the vector Helmholtz equation
to prove that for a solution E, H to the Maxwell equations, both E and H are divergence-free and satisfy the vector Helmholtz equation. Conversely, if E is a solution to the vector Helmholtz equation 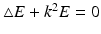 satisfying
satisfying 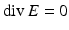 , then E and
, then E and 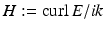 satisfy the Maxwell equations.
satisfy the Maxwell equations.
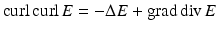 to prove that for a solution E, H to the Maxwell equations, both E and H are divergence-free and satisfy the vector Helmholtz equation. Conversely, if E is a solution to the vector Helmholtz equation
to prove that for a solution E, H to the Maxwell equations, both E and H are divergence-free and satisfy the vector Helmholtz equation. Conversely, if E is a solution to the vector Helmholtz equation 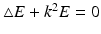 satisfying
satisfying 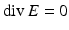 , then E and
, then E and 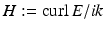 satisfy the Maxwell equations.
satisfy the Maxwell equations.It can be shown that solutions E, H to the Maxwell equations in D satisfying
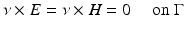
for some open subset 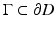 must vanish identically in D.
must vanish identically in D.
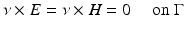
(44)
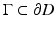 must vanish identically in D.
must vanish identically in D.As a consequence of the Silver–Müller radiation condition, the Stratton–Chu formula is also valid in the exterior domain 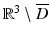 , i.e., we have
, i.e., we have
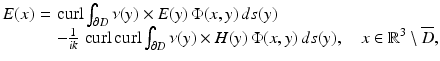
for radiating solutions 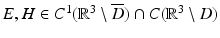 to the Maxwell equations. Again, a corresponding representation for H can be obtained from (45) with the aid of
to the Maxwell equations. Again, a corresponding representation for H can be obtained from (45) with the aid of 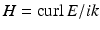 .
.
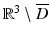 , i.e., we have
, i.e., we have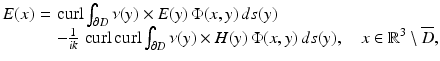
(45)
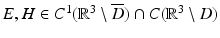 to the Maxwell equations. Again, a corresponding representation for H can be obtained from (45) with the aid of
to the Maxwell equations. Again, a corresponding representation for H can be obtained from (45) with the aid of 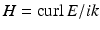 .
.From (45) it can be seen that the radiation condition (41) implies (42) and vice versa. Furthermore, one can deduce that radiating solutions E, H to the Maxwell equations automatically satisfy the Silver–Müller finiteness conditions
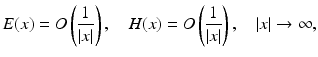
uniformly for all directions and that the validity of the Silver–Müller radiation conditions (41) and (42) is invariant under translations of the origin. From the Helmholtz representation (16) for radiating solutions to the Helmholtz equation and the Stratton–Chu formulas for radiating solutions to the Maxwell equations, it can be deduced that for solutions to the Maxwell equations, the Silver–Müller radiation condition is equivalent to the Sommerfeld radiation condition for the Cartesian components of E and H.
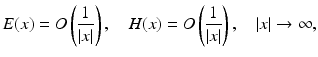
(46)
The Stratton–Chu formula (45) can be used to introduce the notion of the electric and magnetic far-field patterns.
Theorem 6.
Every radiating solution E,H to the Maxwell equations has the asymptotic form
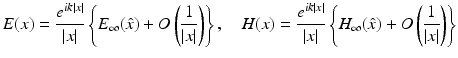
for |x|→∞ uniformly in all directions 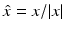 , where the vector fields E ∞ and H ∞ defined on the unit sphere S 2 are called the electric far-field pattern and magnetic far-field pattern, respectively. They satisfy
, where the vector fields E ∞ and H ∞ defined on the unit sphere S 2 are called the electric far-field pattern and magnetic far-field pattern, respectively. They satisfy
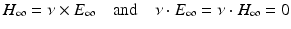
with the unit outward normal ν on S 2. Under the assumptions of (45), we have
![$$\displaystyle{ E_{\infty }(\hat{x}) = \frac{ik} {4\pi } \;\hat{x} \times \int _{\partial D}\left \{\nu (y) \times E(y) + [\nu (y) \times H(y)] \times \hat{ x}\right \}\,e^{-ik\,\hat{x}\cdot y}\,ds(y) }$$](/wp-content/uploads/2016/04/A183156_2_En_48_Chapter_Equ50.gif)
for 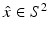 and a corresponding expression for H ∞.
and a corresponding expression for H ∞.
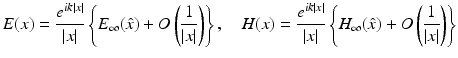
(47)
 , where the vector fields E ∞ and H ∞ defined on the unit sphere S 2 are called the electric far-field pattern and magnetic far-field pattern, respectively. They satisfy
, where the vector fields E ∞ and H ∞ defined on the unit sphere S 2 are called the electric far-field pattern and magnetic far-field pattern, respectively. They satisfy
(48)
![$$\displaystyle{ E_{\infty }(\hat{x}) = \frac{ik} {4\pi } \;\hat{x} \times \int _{\partial D}\left \{\nu (y) \times E(y) + [\nu (y) \times H(y)] \times \hat{ x}\right \}\,e^{-ik\,\hat{x}\cdot y}\,ds(y) }$$](/wp-content/uploads/2016/04/A183156_2_En_48_Chapter_Equ50.gif)
(49)
 and a corresponding expression for H ∞.
and a corresponding expression for H ∞.Rellich’s lemma carries over immediately from the Helmholtz to the Maxwell equations.
Lemma 2.
Let E,H be a radiating solution to the Maxwell equations for which the electric far-field pattern E ∞ vanishes identically. Then E and H vanish identically.
The electromagnetic counterpart of Corollary 1 is given by the following result.
Corollary 2.
Let 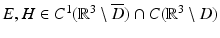 be a radiating solution to the Maxwell equations in
be a radiating solution to the Maxwell equations in 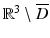 for which
for which
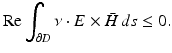 Then
Then 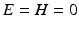 in
in 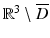 .
.
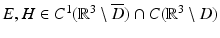 be a radiating solution to the Maxwell equations in
be a radiating solution to the Maxwell equations in 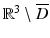 for which
for which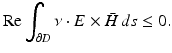
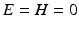 in
in 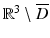 .
.For two vectors 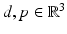 with | d | = 1 and p ⋅ d = 0, the plane waves
with | d | = 1 and p ⋅ d = 0, the plane waves
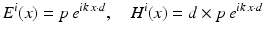
satisfy the Maxwell equations for all 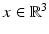 . The orthogonal vectors p and d × p describe the polarization direction of the electric and the magnetic field, respectively. Given the incident field E i , H i and a bounded domain
. The orthogonal vectors p and d × p describe the polarization direction of the electric and the magnetic field, respectively. Given the incident field E i , H i and a bounded domain 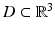 , the simplest obstacle scattering problem is to find the scattered field E s , H s as a radiating solution to the Maxwell equations in the exterior of the scatterer D such that the total field
, the simplest obstacle scattering problem is to find the scattered field E s , H s as a radiating solution to the Maxwell equations in the exterior of the scatterer D such that the total field 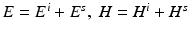 satisfies the perfect conductor boundary condition
satisfies the perfect conductor boundary condition
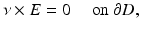
where ν is the outward unit normal to ∂ D. A more general boundary condition is the impedance or Leontovich boundary condition
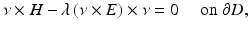
where λ is a positive constant or function called the surface impedance.
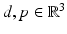 with | d | = 1 and p ⋅ d = 0, the plane waves
with | d | = 1 and p ⋅ d = 0, the plane waves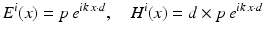
(50)
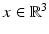 . The orthogonal vectors p and d × p describe the polarization direction of the electric and the magnetic field, respectively. Given the incident field E i , H i and a bounded domain
. The orthogonal vectors p and d × p describe the polarization direction of the electric and the magnetic field, respectively. Given the incident field E i , H i and a bounded domain 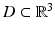 , the simplest obstacle scattering problem is to find the scattered field E s , H s as a radiating solution to the Maxwell equations in the exterior of the scatterer D such that the total field
, the simplest obstacle scattering problem is to find the scattered field E s , H s as a radiating solution to the Maxwell equations in the exterior of the scatterer D such that the total field 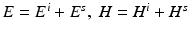 satisfies the perfect conductor boundary condition
satisfies the perfect conductor boundary condition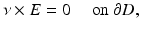
(51)
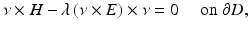
(52)
Theorem 7.
The scattering problem for a perfect conductor has a unique solution.
Proof.
Uniqueness follows from Corollary 2. The existence of a solution again can be based on boundary integral equations. In the layer approach, one tries to find the solution in the form of a combined magnetic and electric dipole distribution
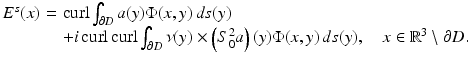
Here S 0 denotes the single-layer operator (29) in the potential theoretic limit case k = 0, and the density a is assumed to belong to the space 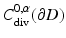 of Hölder continuous tangential fields with Hölder continuous surface divergence. After defining the electromagnetic boundary integral operators M and N by
of Hölder continuous tangential fields with Hölder continuous surface divergence. After defining the electromagnetic boundary integral operators M and N by
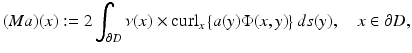
and
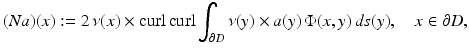
it can be shown that E s given by (53) together with 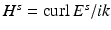 solves the perfect conductor scattering problem provided the density a satisfies the integral equation
solves the perfect conductor scattering problem provided the density a satisfies the integral equation
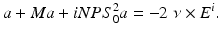
Here the operator P is defined by 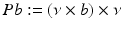 for (not necessarily tangential) vector fields b. Exploiting the smoothing properties of the operator S 0, it can be shown that M + iNPS 0 2 is a compact operator from
for (not necessarily tangential) vector fields b. Exploiting the smoothing properties of the operator S 0, it can be shown that M + iNPS 0 2 is a compact operator from  into itself. The existence of a solution to (56) can now be based on the Riesz–Fredholm theory by establishing that the homogeneous form of (56) only has the trivial solution [22]. ■
into itself. The existence of a solution to (56) can now be based on the Riesz–Fredholm theory by establishing that the homogeneous form of (56) only has the trivial solution [22]. ■
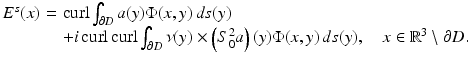
(53)
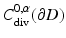 of Hölder continuous tangential fields with Hölder continuous surface divergence. After defining the electromagnetic boundary integral operators M and N by
of Hölder continuous tangential fields with Hölder continuous surface divergence. After defining the electromagnetic boundary integral operators M and N by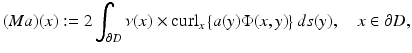
(54)
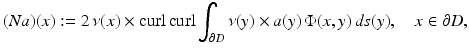
(55)
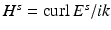 solves the perfect conductor scattering problem provided the density a satisfies the integral equation
solves the perfect conductor scattering problem provided the density a satisfies the integral equation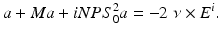
(56)
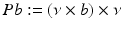 for (not necessarily tangential) vector fields b. Exploiting the smoothing properties of the operator S 0, it can be shown that M + iNPS 0 2 is a compact operator from
for (not necessarily tangential) vector fields b. Exploiting the smoothing properties of the operator S 0, it can be shown that M + iNPS 0 2 is a compact operator from 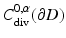 into itself. The existence of a solution to (56) can now be based on the Riesz–Fredholm theory by establishing that the homogeneous form of (56) only has the trivial solution [22]. ■
into itself. The existence of a solution to (56) can now be based on the Riesz–Fredholm theory by establishing that the homogeneous form of (56) only has the trivial solution [22]. ■ Note that, analogous to the acoustic case, without the electric dipole distribution included in (53), the corresponding magnetic dipole integral equation is not uniquely solvable if k is a irregular wave number, i.e., if there exists a nontrivial solution E, H to the Maxwell equations in D satisfying the homogeneous boundary condition ν × E = 0 on ∂ D.
Instead of the classical setting of Hölder continuous functions, the integral equation can also be considered in the Sobolev space 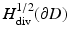 of tangential fields in H 1∕2(∂ D) that have a weak surface divergence in H 1∕2(∂ D) (see [69]).
of tangential fields in H 1∕2(∂ D) that have a weak surface divergence in H 1∕2(∂ D) (see [69]).
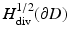 of tangential fields in H 1∕2(∂ D) that have a weak surface divergence in H 1∕2(∂ D) (see [69]).
of tangential fields in H 1∕2(∂ D) that have a weak surface divergence in H 1∕2(∂ D) (see [69]).In addition to electromagnetic obstacle scattering, one can also consider scattering from an inhomogeneous medium where outside a bounded domain D the electric permittivity 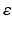 and magnetic permeability μ are constant and the conductivity σ vanishes, i.e.,
and magnetic permeability μ are constant and the conductivity σ vanishes, i.e., 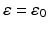 ,
, 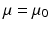 and σ = 0 in
and σ = 0 in 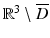 . For simplicity we will assume that the magnetic permeability is constant throughout ℝ 3. Then, again assuming the time-harmonic form (39) with
. For simplicity we will assume that the magnetic permeability is constant throughout ℝ 3. Then, again assuming the time-harmonic form (39) with 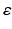 and μ replaced by
and μ replaced by 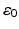 and μ 0, respectively, the total fields
and μ 0, respectively, the total fields 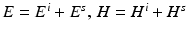 satisfy
satisfy
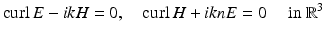
and the scattered wave E s , H s satisfies the Silver–Müller radiation condition, where the wave number is given by 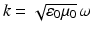 and
and 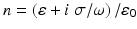 is the refractive index. Establishing uniqueness requires an electromagnetic analogue of the unique continuation principle, and existence can be based on an electromagnetic variant of the Lippmann–Schwinger equation [22].
is the refractive index. Establishing uniqueness requires an electromagnetic analogue of the unique continuation principle, and existence can be based on an electromagnetic variant of the Lippmann–Schwinger equation [22].
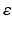 and magnetic permeability μ are constant and the conductivity σ vanishes, i.e.,
and magnetic permeability μ are constant and the conductivity σ vanishes, i.e., 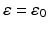 ,
, 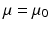 and σ = 0 in
and σ = 0 in 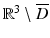 . For simplicity we will assume that the magnetic permeability is constant throughout ℝ 3. Then, again assuming the time-harmonic form (39) with
. For simplicity we will assume that the magnetic permeability is constant throughout ℝ 3. Then, again assuming the time-harmonic form (39) with 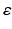 and μ replaced by
and μ replaced by 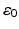 and μ 0, respectively, the total fields
and μ 0, respectively, the total fields 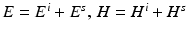 satisfy
satisfy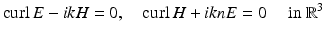
(57)
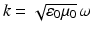 and
and 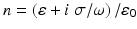 is the refractive index. Establishing uniqueness requires an electromagnetic analogue of the unique continuation principle, and existence can be based on an electromagnetic variant of the Lippmann–Schwinger equation [22].
is the refractive index. Establishing uniqueness requires an electromagnetic analogue of the unique continuation principle, and existence can be based on an electromagnetic variant of the Lippmann–Schwinger equation [22].The scattering of time-harmonic electromagnetic waves by an infinitely long cylinder with a simply connected cross section D leads to boundary value problems for the two-dimensional Helmholtz equation in the exterior  of D. If the electric field is polarized parallel to the axis of the cylinder and if the axis of the cylinder is parallel to the x 3 axis, then
of D. If the electric field is polarized parallel to the axis of the cylinder and if the axis of the cylinder is parallel to the x 3 axis, then
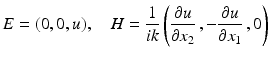 satisfies the Maxwell equations if and only if u = u(x 1, x 2) satisfies the Helmholtz equation. The homogeneous perfect conductor boundary condition is satisfied on the boundary of the cylinder if the homogeneous Dirichlet boundary condition u = 0 on ∂ D is satisfied. If the magnetic field is polarized parallel to the axis of the cylinder, then the roles of E and H have to be reversed, i.e.,
satisfies the Maxwell equations if and only if u = u(x 1, x 2) satisfies the Helmholtz equation. The homogeneous perfect conductor boundary condition is satisfied on the boundary of the cylinder if the homogeneous Dirichlet boundary condition u = 0 on ∂ D is satisfied. If the magnetic field is polarized parallel to the axis of the cylinder, then the roles of E and H have to be reversed, i.e.,
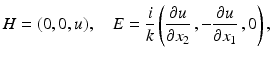 and the perfect conductor boundary condition corresponds to the Neumann boundary condition
and the perfect conductor boundary condition corresponds to the Neumann boundary condition 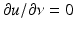 on ∂ D with the unit normal ν to the boundary ∂ D of the cross section D. Hence, the analysis of two-dimensional electromagnetic scattering problems coincides with that of two-dimensional acoustic scattering problems.
on ∂ D with the unit normal ν to the boundary ∂ D of the cross section D. Hence, the analysis of two-dimensional electromagnetic scattering problems coincides with that of two-dimensional acoustic scattering problems.
 of D. If the electric field is polarized parallel to the axis of the cylinder and if the axis of the cylinder is parallel to the x 3 axis, then
of D. If the electric field is polarized parallel to the axis of the cylinder and if the axis of the cylinder is parallel to the x 3 axis, then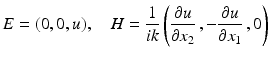
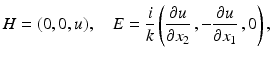
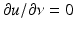 on ∂ D with the unit normal ν to the boundary ∂ D of the cross section D. Hence, the analysis of two-dimensional electromagnetic scattering problems coincides with that of two-dimensional acoustic scattering problems.
on ∂ D with the unit normal ν to the boundary ∂ D of the cross section D. Hence, the analysis of two-dimensional electromagnetic scattering problems coincides with that of two-dimensional acoustic scattering problems. Historical Remarks
Equation (4) carries the name of Helmholtz (1821–1894) for his contributions to mathematical acoustics. The radiation condition (5) was introduced by Sommerfeld in 1912 to characterize an outward energy flux. The expansion (20) was first established by Atkinson in 1949 and generalized by Wilcox in 1956. The fundamental Lemma 1 is due to Rellich (1943) and Vekua (1943). The combined single- and double-layer approach (28) for the existence analysis was introduced independently by Leis, Brakhage and Werner, and Panich in the 1960s in order to remedy the nonuniqueness deficiency of the classical double-layer approach due to Vekua, Weyl, and Müller from the 1950s. Huygens’ principle is also referred to as the Huygens–Fresnel principle and named for Huygens (1629–1695) and Fresnel (1788–1827) in recognition of their contributions to wave optics. The physical optics approximation (34) is named for Kirchhoff (1824–1887) for his contributions to optics. The terms Lippmann–Schwinger equation and Born approximation are adopted from quantum physics. Equation (38) is named for Maxwell (1831–1879) for his fundamental contributions to electromagnetic theory. The radiation conditions (41) and (42) were independently introduced in the 1940s by Silver and Müller. The integral representations (43) and (45) were first presented by Stratton and Chu in 1939. Extending the ideas of Leis, Brakhage and Werner, and Panich from acoustics to electromagnetics, the approach (53) was introduced independently by Knauff and Kress, Jones, and Mautz and Harrington in the 1970s in order to remedy the nonuniqueness deficiency of the classical approach due to Weyl and Müller from the 1950s.
3 Uniqueness in Inverse Scattering
Scattering by an Obstacle
The first step in studying any inverse scattering problem is to establish a uniqueness result, i.e., if a given set of data is known exactly, does this data uniquely determine the support and/or the material properties of the scatterer? We will begin with the case of scattering by an impenetrable obstacle and then proceed to the case of a penetrable obstacle.
From section “Obstacle Scattering,” we recall that the direct obstacle scattering problem is to find 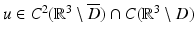 such that the total field
such that the total field 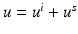 satisfies the Helmholtz equation
satisfies the Helmholtz equation
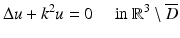
and the sound-soft boundary condition
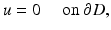
where u i (x) = e ik x⋅ d , | d | = 1, and u s is a radiating solution. We also recall from Theorem 1 that u s has the asymptotic behavior
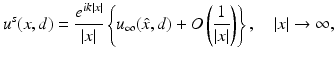
uniformly for all directions 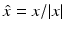 , where u ∞ is the far-field pattern of the scattered field E s . By Green’s integral theorem and the far-field representation (33), it can be shown that the far-field pattern satisfies the reciprocity relation [22]
, where u ∞ is the far-field pattern of the scattered field E s . By Green’s integral theorem and the far-field representation (33), it can be shown that the far-field pattern satisfies the reciprocity relation [22]
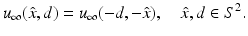
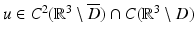 such that the total field
such that the total field 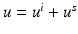 satisfies the Helmholtz equation
satisfies the Helmholtz equation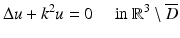
(58)
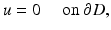
(59)
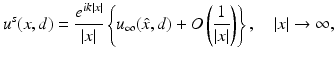
(60)
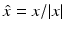 , where u ∞ is the far-field pattern of the scattered field E s . By Green’s integral theorem and the far-field representation (33), it can be shown that the far-field pattern satisfies the reciprocity relation [22]
, where u ∞ is the far-field pattern of the scattered field E s . By Green’s integral theorem and the far-field representation (33), it can be shown that the far-field pattern satisfies the reciprocity relation [22]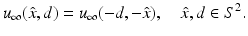
(61)
The inverse scattering problem we are concerned with is to determine D from a knowledge of 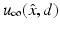 for
for 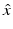 and d on the unit sphere S 2 and fixed wave number k. In particular, for the acoustic scattering problem (58) and (59), we want to show that D is uniquely determined by
and d on the unit sphere S 2 and fixed wave number k. In particular, for the acoustic scattering problem (58) and (59), we want to show that D is uniquely determined by 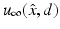 for
for 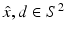 . We note that by the reciprocity relation (61), the far-field pattern u ∞ is an analytic function of both
. We note that by the reciprocity relation (61), the far-field pattern u ∞ is an analytic function of both 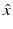 and d, and hence it would suffice to consider u ∞ for
and d, and hence it would suffice to consider u ∞ for 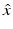 and d restricted to a surface patch of the unit sphere S 2.
and d restricted to a surface patch of the unit sphere S 2.
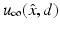 for
for 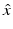 and d on the unit sphere S 2 and fixed wave number k. In particular, for the acoustic scattering problem (58) and (59), we want to show that D is uniquely determined by
and d on the unit sphere S 2 and fixed wave number k. In particular, for the acoustic scattering problem (58) and (59), we want to show that D is uniquely determined by 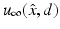 for
for 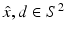 . We note that by the reciprocity relation (61), the far-field pattern u ∞ is an analytic function of both
. We note that by the reciprocity relation (61), the far-field pattern u ∞ is an analytic function of both 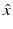 and d, and hence it would suffice to consider u ∞ for
and d, and hence it would suffice to consider u ∞ for 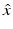 and d restricted to a surface patch of the unit sphere S 2.
and d restricted to a surface patch of the unit sphere S 2.Theorem 8.
Proof.
Let u 1 s and u 2 s be the scattered fields corresponding to D 1 and D 2, respectively. By the analyticity of the scattered field as a function of x and Rellich’s Lemma 1, the scattered fields satisfy u 1 s (⋅ , d) = u 2 s (⋅, d) in the unbounded component G of the complement of 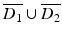 for all d ∈ S 2. This in turn implies that the scattered fields corresponding to
for all d ∈ S 2. This in turn implies that the scattered fields corresponding to 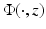 as incident field and D 1 or D 2 as the scattering obstacle satisfy u 1 s (x, z) = u 2 s (x, z) for all x, z ∈ G. Now assume that D 1 ≠ D 2. Then, without loss of generality, there exists x ∗ ∈ ∂ G such that x ∗ ∈ ∂ D 1 and
as incident field and D 1 or D 2 as the scattering obstacle satisfy u 1 s (x, z) = u 2 s (x, z) for all x, z ∈ G. Now assume that D 1 ≠ D 2. Then, without loss of generality, there exists x ∗ ∈ ∂ G such that x ∗ ∈ ∂ D 1 and 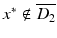 . Then setting
. Then setting 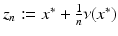 , we have that
, we have that 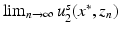 exists but
exists but 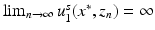 which is a contradiction and hence D 1 = D 2. ■
which is a contradiction and hence D 1 = D 2. ■
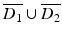 for all d ∈ S 2. This in turn implies that the scattered fields corresponding to
for all d ∈ S 2. This in turn implies that the scattered fields corresponding to 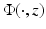 as incident field and D 1 or D 2 as the scattering obstacle satisfy u 1 s (x, z) = u 2 s (x, z) for all x, z ∈ G. Now assume that D 1 ≠ D 2. Then, without loss of generality, there exists x ∗ ∈ ∂ G such that x ∗ ∈ ∂ D 1 and
as incident field and D 1 or D 2 as the scattering obstacle satisfy u 1 s (x, z) = u 2 s (x, z) for all x, z ∈ G. Now assume that D 1 ≠ D 2. Then, without loss of generality, there exists x ∗ ∈ ∂ G such that x ∗ ∈ ∂ D 1 and 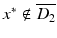 . Then setting
. Then setting 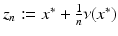 , we have that
, we have that 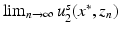 exists but
exists but 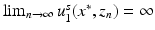 which is a contradiction and hence D 1 = D 2. ■
which is a contradiction and hence D 1 = D 2. ■ An open problem is to determine if one incident plane wave at a fixed wave number k is sufficient to uniquely determine the scatterer D. If it is known a priori that in addition to the sound-soft boundary condition (59) D is contained in a ball of radius R such that kR < 4. 49, then D is uniquely determined by its far-field pattern for a single incident direction d and fixed wave number k [32] (see also [22]). D is also uniquely determined if instead of assuming that D is contained in a ball of sufficiently small radius, it is assumed that D is close to a given obstacle [87]. It is also known that for a wide class of sound-soft scatterers, a finite number of incident fields are sufficient to uniquely determine D [82]. Finally, if it is assumed that D is polyhedral, then a single incident plane wave is sufficient to uniquely determine D [1, 63].
We conclude this section on uniqueness results for the inverse scattering problem for an obstacle by considering the scattering of electromagnetic waves by a perfectly conducting obstacle D. From section “The Maxwell Equations” we recall that the direct obstacle scattering problem is to find 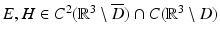 such that the total field
such that the total field 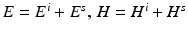 satisfies the Maxwell equations
satisfies the Maxwell equations
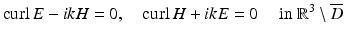
and the perfect conductor boundary condition
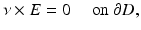
where E i , H i is the plane wave given by (50) and E s , H s is a radiating solution. We also recall from Theorem 1 that u s has the asymptotic behavior
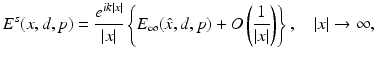
where E ∞ is the electric far-field pattern of the scattered field E s .
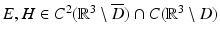 such that the total field
such that the total field 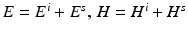 satisfies the Maxwell equations
satisfies the Maxwell equations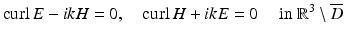
(62)
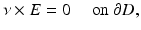
(63)
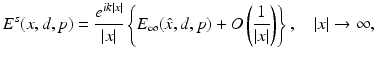
(64)
The inverse scattering problem is to determine D from a knowledge of 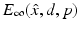 for
for 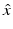 and d on the unit sphere S 2, three linearly independent polarizations p, and fixed wave number k. We note that E ∞ is an analytic function of
and d on the unit sphere S 2, three linearly independent polarizations p, and fixed wave number k. We note that E ∞ is an analytic function of 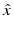 and d and is linear with respect to p. The following theorem can be proved using the same ideas as in the proof of Theorem 8.
and d and is linear with respect to p. The following theorem can be proved using the same ideas as in the proof of Theorem 8.
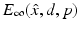 for
for 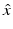 and d on the unit sphere S 2, three linearly independent polarizations p, and fixed wave number k. We note that E ∞ is an analytic function of
and d on the unit sphere S 2, three linearly independent polarizations p, and fixed wave number k. We note that E ∞ is an analytic function of 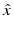 and d and is linear with respect to p. The following theorem can be proved using the same ideas as in the proof of Theorem 8.
and d and is linear with respect to p. The following theorem can be proved using the same ideas as in the proof of Theorem 8.Theorem 9.
Assume that D 1 and D 2 are two perfect conductors such that for a fixed wave number k, the electric far-field patterns for both scatterers coincide for all incident directions d and three linearly independent polarizations p. Then D 1 = D 2.
In the case when D consists of finitely many polyhedra, a single incident wave is sufficient to uniquely determine D [62].
Scattering by an Inhomogeneous Medium
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree