Fig. 1
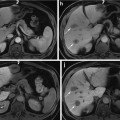
Two axial midsections of the prostate of fat-suppressed T2 MRI from different individuals (the red and green contours delineate the peripheral zone and the central gland respectively) (a, b) and a three-dimensional schematic depiction of the anatomical zones of the prostate (c) [1] © 2006 IEEE
We consider segmentation as a process that consists of two distinct tasks: the localization/recognition of the anatomy of interest and its boundary delineation, as suggested in [2]. Consequently, we suggest a two-staged framework that handles these two tasks separately. For each stage we identify and evaluate potential candidate methods against ground truth. Our evaluation can be regarded as an assessment of the extent of the effectiveness of data-driven methods towards the solution of this particular problem.
The results of the experimental work presented in this chapter demonstrate that the suggested framework can provide results close to the ground truth, without any user interaction, serving as an advanced starting point of an interactive process with a small number of further interactive maneuvers. Moreover, we observe that the framework’s repeatability improves when the segmentation task is tackled in two distinct stages. Parts of the work that is discussed in this chapter have also appeared in [3–5].
Background
Differential Segmentation of the Prostate
The prostate is a gland of the size and shape of a chestnut [6]. It exists only in men and is located immediately below the urinary bladder, where it surrounds a part of the urethra. Its function is the production of a slightly alkaline fluid (40 % of the volume of the semen), which assists towards the neutralization of the acidity of the vaginal tract, thus prolonging the sperm lifespan. In addition, it assists the motility of the sperm cells [6]. Benign prostatic hyperplasia (BPH) is a noncancerous enlargement of the prostate that affects 50 % of men over 60 years old [7]. Approximately a third of them will develop lower urinary tract symptoms, and a quarter of them will need to be operated. For the remaining BPH patients, drug treatment is increasingly utilized [7, 8].
The prostate is anatomically divided into the peripheral (PZ), central (CZ), transitional (TZ), and fibromuscular (FZ) zones. In BPH, the prostatic enlargement is mainly due to the volumetric increase in the TZ. Therefore, the estimation of the TZ volume and the TZ ratio (TZ volume/total prostate volume) is important for monitoring the progress of the disease and the effectiveness of drug treatments [8]. In MRI, two regions are identified: the PZ and the central gland (CG), which includes the other three anatomical zones (Fig. 1). However, in BPH, the TZ is the predominant zone in the CG, due to its expansion, and therefore TZ and CG can be considered as equivalent [1]. Differential segmentation—identifying the surfaces of both the CG and PZ—is challenging. The appearance of the central and peripheral glands varies significantly among individuals (Fig. 1). Furthermore, surrounding tissue (seminal vesicles, blood vessels, the urethra, and the bladder) present contrast challenges at different locations.
While a number of studies recently have addressed segmentation of the prostate in MR images [9–19], segmentation of separate zones has attracted rather less attention [3, 20–24]. These studies fall into two categories: those that employ algorithms trained on multiple image examples in an attempt to model in detail the morphology and shape of the different zones of the prostate and those that tackle the segmentation task interactively. Of the former group, Allen et al. [1] combine a 3-D point distribution model with a Gaussian mixture model, while others apply trained classifiers, such as an evidential C-means classifier in [20] and a Random Forest classifier used within a contextual Markov random field model in [21], or trainable graph-based models [22]. Litjens et al. [18] report that a trained linear discriminant classifier outperforms a multi-atlas approach. Interactive or semi-interactive methods [3, 24] base the segmentation on graphical representations. Given the difficulties in the segmentation task, we have taken the direction in this study of seeking to reduce the workload of interactive methods by leveraging the prior knowledge arising from a single previously segmented example.
Segmentation Propagation from One Image Example
As differential segmentation of the prostate is a challenging task, we assume that expert interaction will be required and investigate methods for minimizing the workload required to achieve a final segmentation. It can often be the case that images are acquired in a sequential (online) manner, rather than being available in a group. In this study we consider the use of a single example as a guide for further segmentations, reducing the level of intervention in subsequent cases. Forward propagation of the template segmentation results in an approximate segmentation for new cases. If this approximate segmentation is accurate, the interactive workload required is correspondingly reduced.
One of the few studies of the literature, which addresses the same problem as we formulate it in this chapter, is the study of Cootes and Taylor in [25]. They adopt a shape representation based on finite element methods (FEMs) [26, 27] when prior knowledge is based on a single image example, whereas they employ an active shape model [28] strategy when multiple image examples are available. When only a single example is available, the allowable shape variation is expressed in terms of the vibrational modes of the FEM model. As further examples are added, this artificial representation of variability is replaced by observed statistical variability.
A single image example is also employed by Rother et al. [29] in a method they call cosegmentation. This denotes simultaneous segmentation of the common parts of a pair of images. In order to tackle this task, they employ an algorithm, which matches the appearance histograms of the common parts of the images. At the same time, the imposition of MRF-based spatial constrains guarantees the spatial coherence of the resulting segmented regions. Results are presented for applications such as video tracking and interactive cosegmentation. Similar ideas have been reported in [30–35]. Most of these methods aim at segmenting 2-D colored natural images. Photographs generally demonstrate good contrast between foreground and background and, due to the variation in color, simple statistics such as color histograms can offer effective discrimination of segments (e.g., [29]). However, histogram-based classification has little to offer in the context of segmentation of greyscale medical images, especially in cases where foreground and background demonstrate similar intensity variations or in case of images with complex appearance.
Active Graph Cuts (AGC) [36] leverages previous segmentations to achieve convergence in a new image in a different way. AGC, when provided with an initial cut, constructs two disjoint subgraphs from the original graph. The initial cut defines the boundary of the two subgraphs. Subsequently, the max-flow/min-cut problem is solved on each of these two subgraphs separately. The combined solution from these subgraphs provides the overall segmentation outcome in the image. We consider and evaluate AGC in our work. To the best of our knowledge, it is the first time that this algorithm is implemented and evaluated independently with respect to its performance on 3-D medical image segmentation tasks.
Atlas-based segmentation is one additional segmentation approach in which often a single image example, termed the atlas, is employed as the prior knowledge about the anatomy of interest [37]. An atlas constitutes a complete description of the geometrical constraints and the neighborhood relationships of the anatomy of interest and is often created by manual segmentation of one image. The segmentation of subsequent images is obtained via registration of the processed image and the atlas. Registration constitutes a procedure, which establishes a point-to-point correspondence between two images [38]. When deformable registration is employed for achieving the dense correspondence of the two images, the atlas is deformed and its labels are mapped onto the processed image, also termed reference image or target image. This process is often referred to as warping, fusion, or matching [38].
One issue associated with frameworks leveraging prior knowledge is the effect of the latter on their performance. If the sample that encapsulates the prior knowledge is representative of the processed population, good results are obtained. However, in the case that it consists of one image, as in this study, the results decline drastically if this image is an outlier with respect to the population. This in turn reduces the framework’s repeatability. This is an issue which has attracted considerable attention in the context of atlas-based segmentation [37]. Solutions towards this problem typically involve the combination of multiple atlases into a mean atlas or alternatively the selection of a single atlas that demonstrates a high degree of similarity with the processed image from a group of atlases. A more recent approach is the multi-atlas label fusion [37]. In the context of this strategy, the segmentation suggestions from multiple atlases onto the target image are utilized as individual classifiers, which are combined via a voting scheme. These approaches improve the repeatability of atlas-based methods. However, they all employ multiple atlases. In our study, we are restricted to utilize one single example as prior knowledge. Therefore, the repeatability issue remains.
In the work presented in this chapter, we follow an approach that is driven by registration, similarly to atlas-based segmentation. However, in order to improve its repeatability, we employ a two-staged strategy, as outlined above. Each of the stages, localization/recognition of the anatomy of interest and delineation of its boundary, is tackled separately. In the first stage, the localization task is tackled via registration; in the second stage, a semi-automatic refinement of the segmentation boundary is realized via graph cuts [39, 40]. We show that adopting this strategy improves the repeatability of the framework (in comparison to the single-stage processing approach) and the sensitivity to unhelpful templates is reduced. While we address this in the context of interactive segmentation, a similar conclusion applies in “automatic” atlas-based segmentation, especially on occasions where a single atlas is employed. In addition, for each stage of our approach we identify and evaluate potential candidate methods against ground truth. Therefore, our study can also serve as a comparative performance evaluation of registration and segmentation strategies. In the next sections, we will discuss further the different components of the suggested framework.
Methods
Figure 2 summarizes our segmentation strategy, its constituent stages, and the operations performed in each of these stages, illustrated here in two-dimensions for the sake of clarity. The segmented example consists of the raw image and a binary mask.
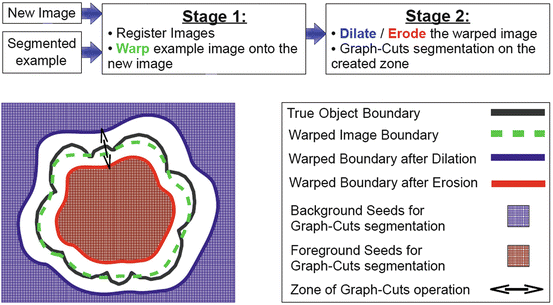

Fig. 2
Overview of the suggested framework
The registration (warping) stage is followed by boundary delineation using graph cuts. As we shall discuss further in the following sections, we employ graph cuts to operate on a zone, which is created via successive erosions and dilations of the warped binary mask produced by the framework’s first stage. This operation aims at the refinement of the boundary of the anatomy of interest, in cases where registration has failed to provide an accurate segmentation boundary.
Dataset
We use a dataset consisting of 22 3-D T2 fat-suppressed MR images of the prostate from individuals with BPH. T2 fat-suppressed MRI provides good contrast not only between the prostate and its surrounding tissue but also between the prostatic anatomical zones. The images were acquired using a 1.5 T Philips Gyroscan ACS MR scanner. After their acquisition, all images were manually cropped close to the prostate (Fig. 3). The ground truth for each image is a binary volumetric mask produced after averaging the manual delineation of two radiologists on the cropped images. Prior to the experiments, the intensities of all images were normalized to lie in the bounded interval [0, 255]. Lastly, all images were resampled to allow for an iso-voxel resolution and volumes of equal sizes to be created.
Localization of the Anatomy of Interest
The framework’s first stage addresses the localization of the anatomy of interest. We evaluate four different registration methods and AGC. In the following paragraphs, we provide the necessary background information with respect to these techniques.
a.
Registration
Registration is a process that establishes a point-to-point correspondence between two images. The images are considered to be identical, but one of them is treated as being corrupted by spatial distortions; therefore, they cannot be aligned in their current form. The two images are known as target and floating image. The terms reference or fixed and template or moving image respectively are also encountered in the literature [38, 41]. The aim of registration is to compute the exact geometrical transformation that the floating image needs to suffer, in order to match the target image. For a more comprehensive review of registration and its constituent components as a framework, readers can refer to the relevant literature (e.g., [38, 41, 42]).
In the context of our framework, the example image plays the role of the template image (Fig. 2). The registration scheme computes the spatial transformation, which best aligns this image to the image to be segmented, denoted as New Image in Fig. 2. Subsequently, the spatial transformation is applied to the template image’s binary mask. The deformed (warped) binary mask constitutes the segmentation suggestion of the framework’s first stage. It also represents the prior knowledge with respect to the segmentation outcome, in the new image’s coordinate system.
The registration methods that we assess are the B-Spline-based registration method of Rueckert et al. which employs nonrigid free-form deformations [43]; Thirion’s demons registration method [44]; the deformable registration method of Glocker et al. [45], which employs MRFs and discrete optimization [46]; and the groupwise registration method of Cootes et al. [47], utilized here in a pair-wise fashion. The implementations of Kroon and Slump [48] were used for the first two registration methods, whereas the authors’ implementations were provided for the latter two methods. In the next paragraphs, we highlight briefly the main components of these registration methods.
The B-Spline method of Rueckert et al. [43] employs a hierarchical transformation model, which combines global and local motion of the anatomy of interest. Global motion is described by an affine transformation, whereas local motion is described by a free-form deformation, which is based on cubic B-Splines. The overall transformation is performed within a multi-resolution setting, which reduces the likelihood of occurrence of a deformation field with invalid topology due to folding of the control points (grid points). The similarity metric employed in this method is normalized mutual information, and the optimization component is based on a gradient descent approach [49].
The underlying concept of the original demons method [44] is that every voxel of the template image is displaced by a local force, which is applied by a demon. The demons of all voxels specify a deformation field, which describes fluidlike free-form deformations; when this field is applied to the template image, the latter deforms so that it matches the reference image. The algorithm operates in an iterative multi-resolution fashion for increased robustness and faster convergence. The original demons algorithm, as presented in [44], is data driven and demonstrates analogies with diffusion models and optical flow equations. Since its original conception, several variants have emerged in the literature [50]. In our study, we use and evaluate the implementation of Kroon and Slump [48], which employs a variant suggested by Vercauteren et al. in [51]. In this variant, the authors follow an optimization approach to demons image registration; more specifically, they employ a gradient descent minimization scheme and operate over a given space of diffeomorphic spatial transformations. Diffeomorphic transformations can be inverted, which is often desirable in image registration. Lastly, Kroon and Slump employ the joint histogram peaks as the similarity metric of their implementation, which allows for the computation of local image statistics [48].
The registration method of Glocker et al. [45], denoted as DROP (deformable image registration using discrete optimization), follows a discrete approach to deformable image registration. Similarly to the method of Ruckert et al., local motion of the anatomy of interest is modeled by cubic B-Splines. The difference, however, is that image registration is reformulated as a discrete multi-labeling problem and modeled via discrete MRFs. In addition, their optimization scheme is based on a primal-dual algorithm, which circumvents the computation of the derivatives of the objective function [46, 52]. This is due to its discrete nature. In their approach, they also follow a multi-resolution strategy, which is based on a Gaussian pyramid with several levels. Moreover, diffeomorphic transformations are guaranteed through the restriction of the maximum displacement of the control points. The authors’ implementation, which is available online [53], features a range of well-known similarity metrics. In this study, the sum of absolute differences was employed.
The registration method of Cootes et al. [47], denoted as GWR, belongs to the groupwise approaches to image registration. Groupwise registration methods aim to establish dense correspondence among a set of images [47], as opposed to pair-wise approaches. In the context of groupwise registration, every image in the set is registered to the mean image, which evolves as the overall process advances. Groupwise registration is often employed in the context of automatic building of shape and appearance models from a group of images, given few annotated examples (e.g., [54]). Conversely, models of shape and appearance can assist registration, when integrated in the process, by imposing certain topological constraints in the spatial deformations. As a result of this integration, Cootes et al. follow a model-fitting approach in their registration method; for each image that is registered to the reference (mean) image, the parameters of the mean texture model are estimated, so that the texture model fits the target image. The overall aim in the process is to minimize the residual errors of the mean texture model with respect to the images of the set. This is achieved via an information theoretic framework, which is based on the minimization of description length (MDL) principle, described in [55]. Piecewise affine transformations are employed for the spatial transformations, which guarantee invertibility of the deformation field. A simple elastic shape model is employed to impose shape constraints to the transformation. Similarly to the previous methods, the registration technique of Cootes et al. follows a multi-resolution approach [47]. In our work, we utilize this method in a pair-wise fashion. We achieve this by employing the reference image to play the role of the mean image. Consequently, the texture and shape model are derived from this single image.
b.
Active Graph Cuts
AGC [36] exploits an approximate segmentation as initialization, in order to compute the optimal final segmentation outcome via max-flow/min-cut algorithms. The authors pose no restriction on the nature of images that this algorithm may process and they claim that convergence is achieved even when the approximate segmentation is very different from the desired one. In the context of our study, this approximate solution is provided by the surface of the segmented example image. While it does not perform registration, AGC does provide a method of propagating an initial segmentation and is a likely candidate method for the first stage of our framework. For the needs of our experimental work, we realized our own implementation of the method in MATLAB®. To the best of our knowledge, this is the first independent implementation and evaluation of this technique in the context of 3-D medical image segmentation. In the following paragraphs, we provide further details about the method.
AGC is a graph-based method; therefore, in the context of this technique, an image is represented as a graph. Its initialization, termed “initial cut”, is a set of contiguous graph edges, which separates the overall graph into two subgraphs that form two independent flow networks. The vertices adjacent to the initial cut are connected to the source graph terminal. Their t-link weight is equal to the capacity of the adjacent graph edge, which is part of the initial cut. In order to solve the max-flow/min-cut problem, different algorithms may be employed. In [36], the authors suggest a preflow-push [56] approach to tackle this problem on the subgraphs. Preflow-push strategies operate locally and thus flood the network gradually. This in turn generates intermediate cuts as the algorithm progresses. However, in our work, we are rather interested in the final min-cut instead of the intermediate cuts. Therefore, we employ an implementation of a max-flow/min-cut algorithm [57], which follows the augmenting paths approach as described in [58]. The final segmentation outcome is provided by the aggregation of the solutions of the max-flow/min-cut problem on the two subgraphs.
The authors provide no instruction about the positioning of the sink graph terminal on the two subgraphs in [36]. In our work, we observed that different choices may significantly affect the segmentation outcome. For the sake of consistency, with respect to this problem, in all our experiments, the voxels at the image borders were connected to the sink graph terminal of the subgraph that lies outside the initial cut, whereas for the subgraph that is contained by the initial cut, the voxels at a fixed distance, using a distance transform, from the centroid of the initial cut were connected to the sink.
Delineation of the Anatomical Boundary
In the previous sections, we highlighted the candidate methods for the first stage of our framework: localization of the anatomy of interest in the “New Image” of Fig. 2. The second stage of our framework aims for the delineation of an accurate boundary of the anatomy of interest, given the output of the first stage as initialization.
In a previous study [57], we demonstrated that graph cuts segmentation [39, 40] offers significant advantages over several other methods in the context of interactive segmentation. In the work presented in this chapter, we employ graph cuts in a semi-automated fashion to refine the boundary of the anatomy of interest. As shown in Fig. 2, graph cuts (GC) operates in a zone that surrounds the initial boundary defined by successive erosions and dilations of the initial binary segmentation. Erosion and dilation are morphological operations, which result into contraction and expansion of a binary object respectively [59]. The width of the zone is controlled via a user-defined parameter and depends on the number of erosions and dilations performed on the segmented image example. This is the only interaction that takes place during delineation of the anatomy of interest.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree