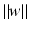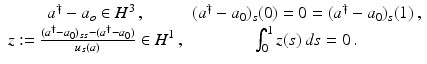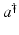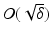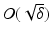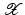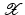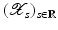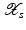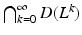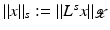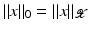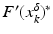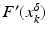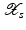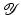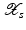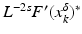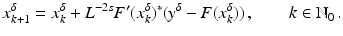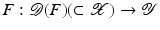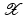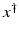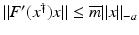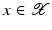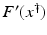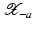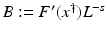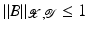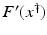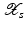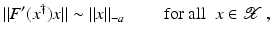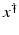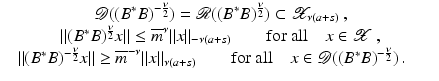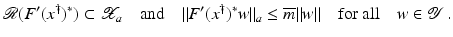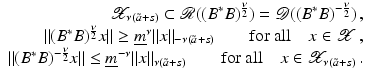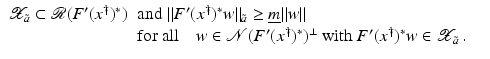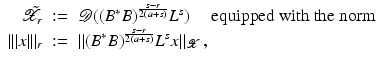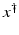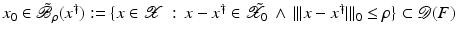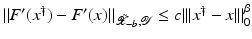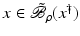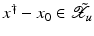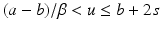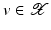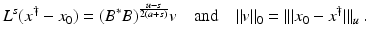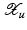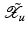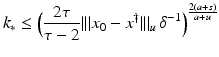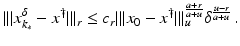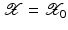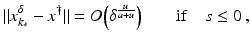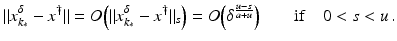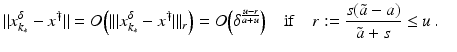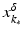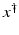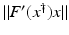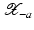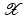(1)
where
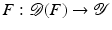 with domain
with domain 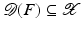 . The exposition will be mainly restricted to the case of
. The exposition will be mainly restricted to the case of 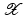 and
and 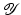 being Hilbert spaces with inner products
being Hilbert spaces with inner products 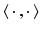 and norms
and norms 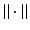 . Some references for the Banach space case will be given.
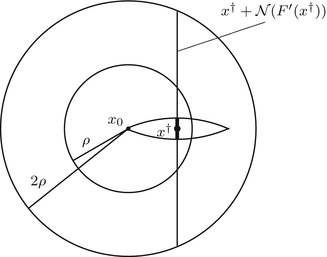
. Some references for the Banach space case will be given.We will assume attainability of the exact data y in a ball 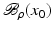 , i.e., the equation F(x) = y is solvable in
, i.e., the equation F(x) = y is solvable in 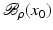 . The element x 0 is an initial guess which may incorporate a-priori knowledge of an exact solution.
. The element x 0 is an initial guess which may incorporate a-priori knowledge of an exact solution.
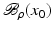 , i.e., the equation F(x) = y is solvable in
, i.e., the equation F(x) = y is solvable in 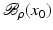 . The element x 0 is an initial guess which may incorporate a-priori knowledge of an exact solution.
. The element x 0 is an initial guess which may incorporate a-priori knowledge of an exact solution.The actually available data y δ will in practice usually be contaminated with noise for which we here use a deterministic model, i.e.,
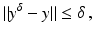
where the noise level δ is assumed to be known. For a convergence analysis with stochastic noise, see the references in section “Further Literature on Gauss–Newton Type Methods”.
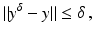
(2)
2 Preliminaries
Conditions on F
For the proofs of well-definedness and local convergence of the iterative methods considered here we need several conditions on the operator F. Basically, we inductively show that the iterates remain in a neighborhood of the initial guess. Hence, to guarantee applicability of the forward operator to these iterates, we assume that
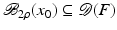
for some ρ > 0.
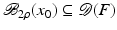
(3)
Moreover, we need that F is continuously Fréchet-differentiable, that 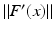 is uniformly bounded with respect to
is uniformly bounded with respect to 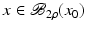 , and that problem (1) is properly scaled, i.e., certain parameters occurring in the iterative methods have to be chosen appropriately in dependence of this uniform bound.
, and that problem (1) is properly scaled, i.e., certain parameters occurring in the iterative methods have to be chosen appropriately in dependence of this uniform bound.
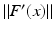 is uniformly bounded with respect to
is uniformly bounded with respect to 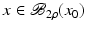 , and that problem (1) is properly scaled, i.e., certain parameters occurring in the iterative methods have to be chosen appropriately in dependence of this uniform bound.
, and that problem (1) is properly scaled, i.e., certain parameters occurring in the iterative methods have to be chosen appropriately in dependence of this uniform bound.The assumption that F ′ is Lipschitz continuous,
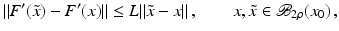
that is often used to show convergence of iterative methods for well-posed problems, implies that
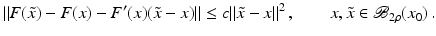
However, this Taylor remainder estimate is too weak for the ill-posed situation unless the solution is sufficiently smooth (see, e.g., case (ii) in Theorem 9 below). An assumption on F that can often be found in the literature on nonlinear ill-posed problems is the tangential cone condition
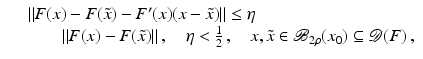
which implies that
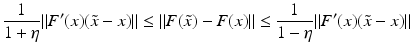 for all
for all 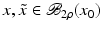 . One can even prove (see [70, Proposition 2.1]).
. One can even prove (see [70, Proposition 2.1]).
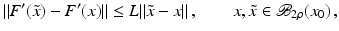
(4)
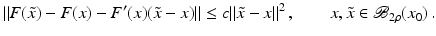
(5)
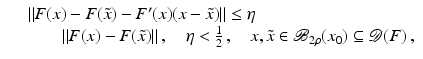
(6)
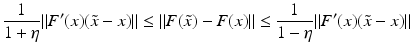
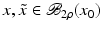 . One can even prove (see [70, Proposition 2.1]).
. One can even prove (see [70, Proposition 2.1]).Proposition 1.
Let 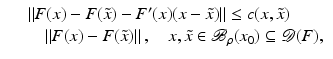
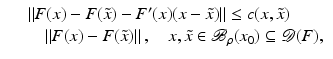
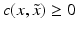 , where
, where 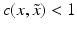 if
if 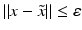 .
.(i)
Then for all 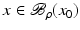
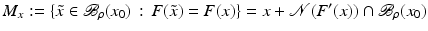 and
and 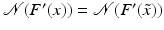 for all
for all 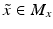 . Moreover,
. Moreover,
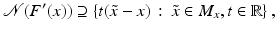 where instead of
where instead of 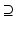 equality holds if
equality holds if 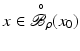 .
.
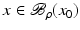
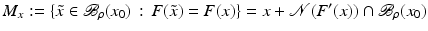
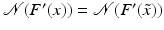 for all
for all 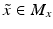 . Moreover,
. Moreover,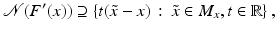
 equality holds if
equality holds if 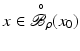 .
.(ii)
If F(x) = y is solvable in 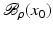 , then a unique x 0 -minimum-norm solution exists. It is characterized as the solution
, then a unique x 0 -minimum-norm solution exists. It is characterized as the solution 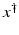 of F(x) = y in
of F(x) = y in 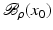 satisfying the condition
satisfying the condition
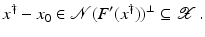
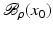 , then a unique x 0 -minimum-norm solution exists. It is characterized as the solution
, then a unique x 0 -minimum-norm solution exists. It is characterized as the solution 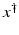 of F(x) = y in
of F(x) = y in 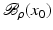 satisfying the condition
satisfying the condition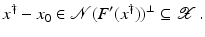
(7)
If F(x) = y is solvable in 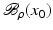 but a condition like (6) is not satisfied, then at least existence (but no uniqueness) of an x 0-minimum-norm solution is guaranteed provided that F is weakly sequentially closed (see [36, Chapter 10]).
but a condition like (6) is not satisfied, then at least existence (but no uniqueness) of an x 0-minimum-norm solution is guaranteed provided that F is weakly sequentially closed (see [36, Chapter 10]).
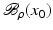 but a condition like (6) is not satisfied, then at least existence (but no uniqueness) of an x 0-minimum-norm solution is guaranteed provided that F is weakly sequentially closed (see [36, Chapter 10]).
but a condition like (6) is not satisfied, then at least existence (but no uniqueness) of an x 0-minimum-norm solution is guaranteed provided that F is weakly sequentially closed (see [36, Chapter 10]).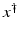
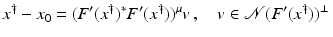
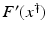
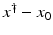
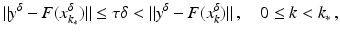
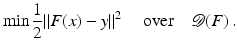
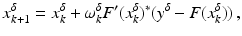
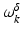
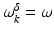
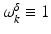
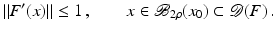
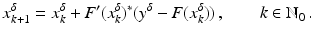
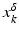
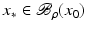
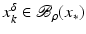
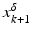
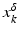
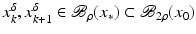 .
.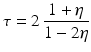
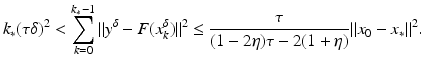
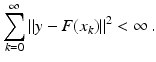
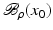
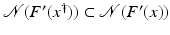
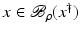
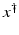
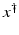
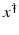
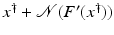
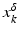
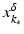
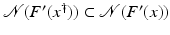
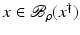
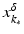
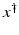
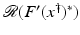
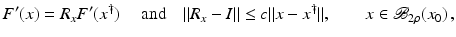
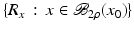
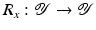
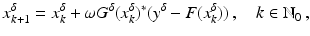
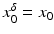
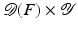
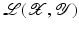
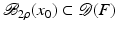
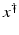
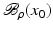
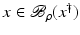
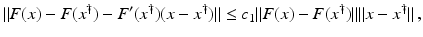
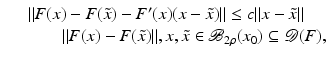
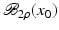
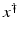
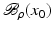
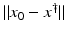
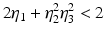
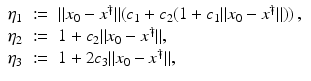
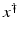
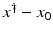
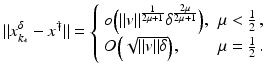
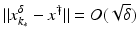
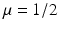
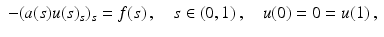
![$$\displaystyle\begin{array}{rcl} F^{{\prime}}(a)h& =& A(a)^{-1}[(hu_{ s}(a))_{s}]\,, {}\\ F^{{\prime}}(a)^{{\ast}}w& =& -B^{-1}[u_{ s}(a)(A(a)^{-1}w)_{ s}]\,, {}\\ \end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_9_Chapter_Equ26.gif)
![$$\displaystyle\begin{array}{rcl} A(a): H^{2}[0,1] \cap H_{ 0}^{1}[0,1]& \rightarrow & L^{2}[0,1] {}\\ u& \mapsto & A(a)u:= -(au_{s})_{s} {}\\ \end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_9_Chapter_Equ27.gif)
![$$\displaystyle\begin{array}{rcl} B: \mathcal{D}(B):=\{\psi \in H^{2}[0,1]\,:\,\psi ^{{\prime}}(0) =\psi ^{{\prime}}(1) = 0\}& \rightarrow & L^{2}[0,1] {}\\ \psi & \mapsto & B\psi:= -\psi ^{{\prime\prime}}+\psi \,; {}\\ \end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_9_Chapter_Equ28.gif)
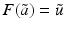
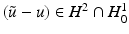
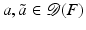
![$$\displaystyle\begin{array}{rcl} & & \langle \,F(\tilde{a}) - F(a) - F^{{\prime}}(a)(\tilde{a} - a),w)\,\rangle _{ L^{2}}\qquad \qquad {}\\ & & \quad =\langle \, (\tilde{u} - u) - A(a)^{-1}[((\tilde{a} - a)u_{ s})_{s}],w\,\rangle _{L^{2}} {}\\ & & \quad =\langle \, A(a)(\tilde{u} - u) - ((\tilde{a} - a)u_{s})_{s},A(a)^{-1}w\,\rangle _{ L^{2}} {}\\ & & \quad =\langle \, ((\tilde{a} - a)(\tilde{u}_{s} - u_{s}))_{s},A(a)^{-1}w\,\rangle _{ L^{2}} {}\\ & & \quad = -\langle \,(\tilde{a} - a)(\tilde{u} - u)_{s},(A(a)^{-1}w)_{ s}\,\rangle _{L^{2}} {}\\ & & \quad =\langle \, F(\tilde{a}) - F(a),((\tilde{a} - a)(A(a)^{-1}w)_{ s})_{s}\,\rangle _{L^{2}}\,. {}\\ \end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_9_Chapter_Equ29.gif)
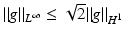
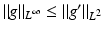
![$$\displaystyle\begin{array}{rcl} & & \|F(\tilde{a}) - F(a) - F^{{\prime}}(a)(\tilde{a} - a)\|_{ L^{2}}\quad \\ & & \quad \leq \sup _{\|w\|_{ L^{2}}=1}\langle \,F(\tilde{a}) - F(a),((\tilde{a} - a)(A(a)^{-1}w)_{ s})_{s}\,\rangle _{L^{2}} \\ & & \quad \leq \| F(\tilde{a}) - F(a)\|_{L^{2}}\sup _{\|w\|_{ L^{2}}=1}\Big[\Big\|\Big(\frac{\tilde{a} - a} {a} \Big)_{s}\Big\|_{L^{2}}\|a(A(a)^{-1}w)_{ s}\|_{L^{\infty }} \\ & & \qquad +\,\Big\| \frac{\tilde{a} - a} {a} \Big\|_{L^{\infty }}\|w\|_{L^{2}}\Big] \\ & & \quad \leq \underline{a}^{-1}(1 + \sqrt{2} + \underline{a}^{-1}\sqrt{2}\|a\|_{ H^{1}})\|F(\tilde{a}) - F(a)\|_{L^{2}}\|\tilde{a} - a\|_{H^{1}}\,.\qquad {}\end{array}$$](/wp-content/uploads/2016/04/A183156_2_En_9_Chapter_Equ30.gif)
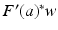
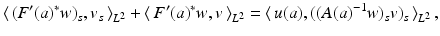
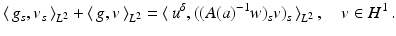
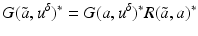
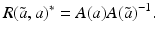
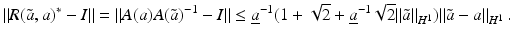
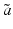
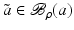
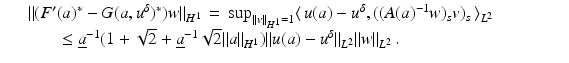
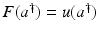
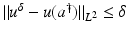
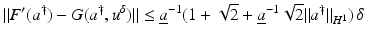
![$$\displaystyle{a^{\dag }- a_{ 0} = -B^{-1}[u_{ s}(a^{\dag })(A(a^{\dag })^{-1}w)_{ s}]}$$](/wp-content/uploads/2016/04/A183156_2_En_9_Chapter_Equs.gif)