of water and lipid tissue in humans and animal models. A wealth of information can be added to these parameters using MR spectroscopy (MRS) since levels of metabolites can in vivo be detected with this technique. In fact, for mice brain, levels of up to 17 metabolites can be detected using proton MRS (see Note 1), which can be used for understanding metabolism in fundamental research or used as diagnostic markers (1). Mice are of special interest because numerous (transgenic) mouse models are available to investigate metabolism or to mimic pathology (2). Figure 1 shows an example of a proton MR spectrum obtained from a 4 μL volume in the cortex/hippocampus of a mouse brain, illustrating a number of detectable metabolites.
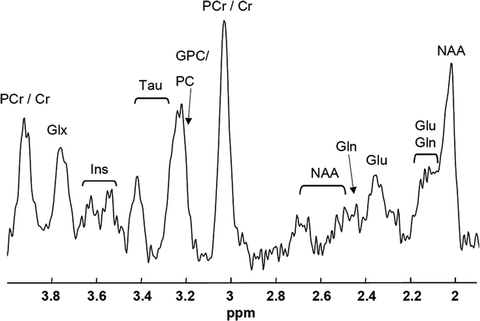
Fig. 1.
MR spectrum obtained from a 4 μL volume in the cortex/hippocampus of a mouse brain at 7 T (23). Clear resonances can be depicted of NAA, glutamate (Glu), glutamine (Gln), (phospho-) creatine (PCr/Cr), (glycero-)phospocholine (GPC/PC), taurine (Tau), and myo-inositol (Ins).
Spatial mapping of metabolism benefits research in brain metabolism even further (3); however, most of the published proton MR spectra of mice brain are obtained from single volume elements (voxel). Limiting the detection to a single voxel allows focused optimization of the MR system in maximizing the quality of the MR spectrum, whereas spatial mapping of metabolism over a larger field of view (FOV) requires more technical challenges to overcome. Especially in the mouse brain, this is challenging due to its small size.
MRSI data of good quality has to meet quite a few prerequisites (1). First of all, the signal-to-noise ratio (SNR) needs to be sufficient to detect metabolic alterations with respect to controls. Secondly, good B 0 shim needs to be obtained to minimize linewidths of the peaks in order to reduce signal overlap, thereby enabling distinct detection of metabolites (4). Thirdly, the signals from the highly concentrated water content have to be accurately suppressed not only to overcome dynamic range limitations of the MR receiver but also to reduce spectral contamination caused by potential vibrations, eddy currents, and (physiologic) motion (5). Fourthly, contaminating signals originating from areas outside the volume of interest need to be suppressed to below noise level as these may leak into the voxels of interest due to the point spread function in spatial Fourier transform. Fifthly, the actual spatial resolution should be sufficient to obtain metabolic information from distinct anatomical areas. Finally, nonuniformities in spin excitation, spin relaxation, and signal reception both in spatial and spectral domain should be known and accounted for when analyzing the data.
Although MRSI of the mouse brain is feasible, artifacts in spectra can easily occur if the acquisition methods are not optimized properly (6). In MRSI, spectra are obtained from a relatively large area, therefore B 0 shimming has to be optimized for the entire region of interest. However, if a small part of this area includes tissue transitions with substantial differences in susceptibility (e.g., brain–air transition in ear cavities in mice results in inhomogeneities), the B 0 shimming using conventional shim systems (up to third-order shim coils) will be poor, leading to broad and overlapping peaks in the spectra.
When regions of interest are selected that exclude large susceptibility transitions (e.g., the centre of the brain), B 0 shimming can be excellent over the entire region of interest. As such, spectral resolution will be optimal and chemical shift-selective water suppression can be obtained relatively easily. Outside the region of interest, however, the B 0 shim is not optimal, leading to off resonances of the spins. Water suppression will therefore be insufficient leading to high remaining signals of water with a high probability that these will shift into the spectral range of the metabolites of interest. These signals can contaminate the spectra in the region of interest due to voxel bleeding caused by spatial Fourier transform.
Another potential artifact originates from highly concentrated lipids at the skull, generally outside the region of interest. With only chemical shift-selective water suppression techniques, these signals will not be attenuated and may therefore leak into the voxels of interest by spatial Fourier transform.
Both hardware and pulse sequences have been developed to meet the challenges in MRSI of the mouse brain, overcoming most of the limitations described above. In this chapter, the basics of spectroscopic imaging are described including application of filtering to reduce voxel bleeding. In addition, pulse sequences are discussed that use spatially selective spin perturbation, thereby excluding unwanted signals outside the region of interest. Finally, dedicated hardware for mice MRSI in terms of RF coils and B 0 shims are briefly discussed.
2 Materials
2.1 Scanner and Animal Handling
Compared to the rat or the human brain, the mouse brain is relatively small; thus the number of spins that contribute to the signal is relatively low, potentially resulting in a low SNR. The strength of the magnet that is used to obtain MR spectra of the mouse brain is therefore generally at least 7 T, but preferably even stronger. The bore size must be at least the size of the mouse, including space for the RF coils and gradient system. For example, a magnet bore size of 12 cm can be used with a gradient set of 8 cm and an RF coil of 6 cm, still enabling the positioning of the mouse.
Although a larger bore size may be beneficial for positioning the mouse, it may result in higher costs and reduced gradient strength performance. For mouse MRS, small voxel sizes are required that can only be effectively obtained with strong gradients. Therefore at least 200 mT/m of gradient strength is recommended for MRS(I) of the mouse brain (see Note 2).
The ideal RF coil setup for mouse MRSI would be a volume transmit coil, which can generate a uniform B 1 field for spin excitation/manipulation, with an array of local receiver coils for maximum SNR (7). It should be considered, however, that whole body volume coils are not very efficient in obtaining strong B 1 fields resulting in a low bandwidth with severe chemical shift displacement artifacts (as described below). The use of RF amplifiers with more peak power can overcome this issue, but also a dedicated (small-size) mouse headcoil would help. On the signal reception side, it should also be pointed out that an array may not be that efficient, even compared to a single loop coil. In mouse brain imaging, the tissue losses do not dominate the coil losses; adding multiple elements will therefore add more noise to the data (8). However, when parallel imaging in MRSI is required, multi-element arrays are essential. Nevertheless, when SNR is crucial, the receiver coil should be positioned as close as possible to the tissue of interest.
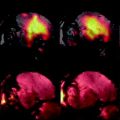
Finally, the mouse has to be positioned in the coil setup, while being kept under anesthesia for the duration of the experiment. As these experiments may take hours, the temperature of the mouse has to be regulated as well, since mice are unable to maintain body temperature under these conditions. Figure 2 shows an illustration of a setup that can be used for MRSI of the mouse brain using a surface coil and anesthetics system mounted on an animal tray that can be shifted inside the MR system. A gas mixture of 1–2% of isoflurane with a 50–50% mixture of O2 and N2 gas may be applied to the mouse using a gas mask. Hot water can be pumped through a mouse bed to warm the mouse, while rectum thermometry is used to control the temperature. All cables, water tubes and gas lines are guided through a filter plate at the end of the bore of the magnet, to prevent RF noise sources entering the bore.


Fig. 2.
Experimental setup that can be used for MRSI of the mouse brain. The RF coil is ideally positioned close to the mouse brain while the mouse is kept under anesthesia using a gas mask. The temperature of the mouse is controlled by circulating warm water through a dedicated mouse bed and monitored using fiber optic rectal thermometry. The setup is positioned in the magnet via a probe platform, the cables and tubes of which are interfaced through an RF filter box.
2.2 Basic Scanning Considerations
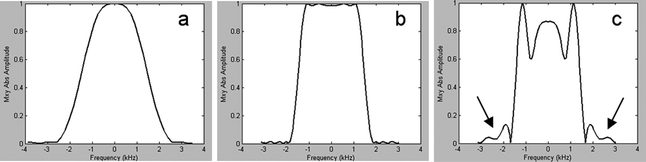
In analogy with phase encoding in MRI, spatial information in spectroscopic imaging can be obtained by phase encoding of the excited spins using an array of B 0 gradient settings (9). For each spatial dimension (i.e., x-, y-, and z-axes), a unique number of N phase encoding steps are required to encode the data in that dimension in N spatial segments. The dataset is stored into an array called k-space. The nominal dimensions of the segments (voxel size) and field of view (FOV) of the encoded spatial domain are related as voxel size = FOV/N. The actual dimensions are related to the gradient strength and length used to encode the spins. In particular, the step size of the gradient (dGt) defines the FOV, whereas the maximum gradient change (i.e., dGt × N) defines the pixel size with dGt = 1/γFOV, where Gt is the integral of the gradient over its duration t and γ the gyromagnetic ratio of the nuclear spin. Spatial information can be decoded from the dataset in k-space by fast Fourier transform (FFT) of each spatial dimension. Since the number of gradient steps is limited, FFT will result in point spread artifacts; i.e., signals originating from a voxel will leak into other voxels (voxel bleeding, Fig. 3). Such leakage may be reduced by application of filters like Hamming, but will result in broadening of the voxel dimension (i.e., for a 3D Hamming filtered SI dataset with a nominal voxel size of 1 mm in all dimensions, this would lead to a voxel of a sphere with a diameter of 1.78 mm) (10).
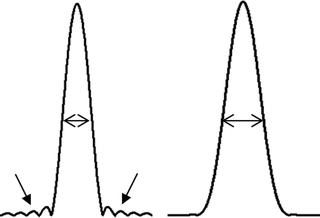

Fig. 3.
Effects of point spread without (left) and with (right) Hamming filtering. Application of a Hamming filter results in a broader voxel size; however, contamination of signals from outside this voxel (voxel bleeding) is substantially reduced (see arrows).
As a unique phase-encoding step is required to encode spins in spatial domain, a three-dimensionally encoded dataset consists of a k-space matrix of N x N y N z data lines. Each line is obtained by acquisition of the signals from the excited spins. The acquisition will be repeated N x N y N z times leading to a scan duration of N x N y N z TR (with TR being the repetition time that elapses between two acquisitions). In case spectra are required from the entire mouse brain with a FOV of 16 × 16 × 8 mm3 at a resolution of 1 mm3 with a TR of 5 s, a typical 3D MRSI sequence would take 16 × 16 × 8 × 5 s = 3 h.
Scan times can be reduced by decreasing TR; however, the signal intensities acquired will have a stronger dependence on the T 1 of the specific spins making quantification more challenging. Proton echo planar spectroscopic imaging (PEPSI) can be applied to reduce scan time by one dimension (11). In this method, as in MRI, a readout gradient is applied during the acquisition of the data lines. To maintain spectral information, each data point in the time domain is obtained with the same balanced readout gradient.
FOV can be reduced to reduce scan time, but care must be taken not to excite spins outside the FOV for these will fold into the region of interest as a consequence of phase wrap. Using an array of receiver coils, these wraps can still be unfolded by means of SENSE reconstruction (12). Slice-selective excitation can also be applied to reduce scan times, as spatial encoding can be omitted in one dimension.
2.3 Volume Selection
As a consequence of voxel bleeding by spatial FFT, signals outside the region of interest need to be excluded to prevent contamination of the spectra of interest. The most effective methods combine spectroscopic imaging with volume selection and refocusing techniques, like stimulated echo acquisition method (STEAM) (13) or point resolved spectroscopy (PRESS) (14). With STEAM, a combination of three orthogonally oriented slice selective radio frequency (RF) pulses are applied. Stimulated echoes from these three RF pulses result in a detectable echo signal that originates from the cross section of the three slices. With PRESS, a slice-selective RF pulse is succeeded with two orthogonally oriented slice-selective refocusing pulses resulting in two echoes of which the second detectable echo originates from the cross section of the three slices. Intrinsically PRESS can give twice the SNR compared to STEAM (see Note 3) but may come with potentially more artifacts.
A slice-selective RF pulse is obtained with a B 0 gradient applied in conjunction with an RF pulse. The bandwidth of the RF pulse (BW, in hertz) combined with the gradient strength (G, in mT/m) defines the thickness (d, in mm) of the slice by d = BW/(γ·G), where γ is the gyromagnetic ratio of the nuclear spin (i.e., 42.56 MHz/T for 1H spins). The slice position (p, in mm) with respect to the isocenter of the magnet can be controlled by setting the offset frequency (Δf, in Hz) of the RF pulse to Δf = BW·p/d.
Spins of metabolites with different chemical shifts will experience a different offset frequency between their Larmor frequency and the selected frequency of the RF pulse. The position of the slice will therefore be different for metabolites with different chemical shifts, which is called chemical shift displacement artifact (CSDA). This is expressed as the relative mismatch of the slice position over the entire chemical shift range (Δσ, in ppm) of the metabolites of interest as CSDA = Δσ·γ·B 0/BW. By maximizing the bandwidth of the RF pulse (see Note 2), the chemical shift displacement artifact can be minimized (15).
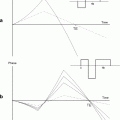
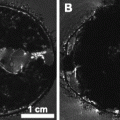
Apart from a minimum CSDA, the slice profile needs to be appropriate to not only uniformly perturb the spins within the slice, but also exclude excitation of spins outside the selected slice. Inverse FFT can be applied to calculate the RF pulse shape for small tip angles. As can be predicted by the nonlinear behavior of the Bloch equations, Shinnar–le Roux optimizations need to be applied to calculate these RF pulses for the larger tip angles used in MR spectroscopy (16). When assuming a uniform B 1 field over the entire subject of investigation, the maximum bandwidth of these RF pulses is related to the maximum B 1 field that can be obtained with the MR system, whereas the transition from full perturbation to no excitation can be minimized by maximizing the length of the RF pulse (Fig. 4a and b). This will have a consequence for the minimum echo time that can be obtained. When the B 1 field over the entire subject is not uniform or does not match the expected B 1 field, the slice profile itself becomes a function of the actual B 1 strength (Fig. 4c). Not only do the spins inside the selected slice have a deviated perturbation, but also spins outside the slice are partially being excited, giving rise to unwanted signals or artifacts. At lower flip angles, e.g., 90°, in a STEAM sequence, this effect is less severe than in a PRESS sequence that uses two 180° pulses. Another option would be to adapt the PRESS sequence into an adiabatic version like a LASER sequence (localization by adiabatic selective refocusing), which is not sensitive to B 1 nonuniformities. This method, however, requires substantially longer and more RF pulses which has a consequence for the TE (17). Figure 5 shows an MRSI dataset obtained with STEAM selection of the mouse brain.