The BOLD Effect

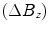an applied field $\left[{B_o}\right]$ ” (7). Schenck goes on to highlight that only a perturbation parallel $\left(\Delta {B_z}\right)$ to the applied field is relevant in NMR and that the perturbation is strongest within or at the surface of the object leading to 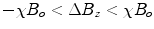$- \chi {B_o} < \Delta {B_z} < \chi {B_o}$ and an estimation of 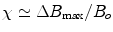$\chi \simeq \Delta {B_{\max }}/{B_o}$ . From this definition, it is easily surmised that a material with magnetic susceptibility 10 times that of another material can perturb the applied field, and hence resonant frequency of nearby spins, ten times as much.

During imaging, every proton inside the body is exposed to a magnetic field which, at any given time, could be composed of the static main field, the RF excitation field, gradient fields to achieve spatial localization, and a localized internal field based on that proton’s location relative to other endogenous and exogenous tissues and materials. The localized internal field is dominated by the neighboring atomic electrons (8) and associated magnetic moments. Following Lenz’s law, all of the electrons exposed to a magnetic field experience an alteration in their orbital motion which results in the induced magnetic field opposing the applied field. 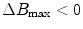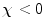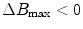This mechanism of an opposing magnetization is called diamagnetism and would result in $\Delta {B_{\max }} < 0$ , i.e., $\chi < 0$ . 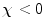Diamagnetism is ubiquitous in all materials and therefore is aptly described by Schenck (7) as the “default mechanism” that determines a material’s magnetic susceptibility, with the caveat, “unless it is overridden by some more powerful mechanism,” e.g., paramagnetism.

Paramagnetism arises when materials are present that have unpaired electrons. Returning to one’s first chemistry class, electrons in an atom are organized such that the spin moments of each pair cancel. Non-zero magnetic moments are therefore only present in materials with unpaired electrons. In the absence of an externally applied field, these moments are randomly distributed. However, upon interaction with an externally applied field, the moments tend to align with the applied field, thereby augmenting the local magnetic field, i.e., $$$\Delta {B_{\max }} > 0$$” src=”/wp-content/uploads/2017/02/A184233_1_En_8_Chapter_IEq8.gif”></SPAN> and <SPAN id=IEq9 class=InlineEquation><IMG alt=$ 0$$” src=”/wp-content/uploads/2017/02/A184233_1_En_8_Chapter_IEq9.gif”>. The paramagnetic response of unpaired electrons (spin alignment) can swamp the diamagnetic response of paired electrons (orbital motion) in surrounding material/tissue. Although a single paramagnetic ion could cancel the diamagnetism of thousands of surrounding water molecules, more often than not, such ions are found in trace amounts in tissue and therefore largely do not supersede the bulk diamagnetism. 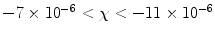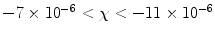As a result, the magnetic susceptibility of most tissues falls within the range of: $- 7 \times {10^{ - 6}} < \chi < - 11 \times {10^{ - 6}}$ (7).

An example of an exogenous paramagnetic material commonly used in NMR imaging to achieve certain contrast in the image is gadolinium which has unpaired electrons in the f-shell. An example of an endogenous paramagnetic material commonly used in NMR imaging to achieve certain contrast in the image is deoxyhemoglobin which has unpaired electrons present in the heme complex.

The third magnetic susceptibility class of materials, ferromagnetic materials, are not discussed since no such materials are naturally found in vivo. Ferromagnetic materials such as nickel and iron have very high susceptibilities of ∼600 and 200,000, respectively, due to unpaired electrons in ordered structures (7).

2 Magnetic Susceptibility In Vivo

2.1 What Is the Source of Magnetic Susceptibility In Vivo?

The proteins of the globin superfamily may not share an evolutionarily conserved sequence but they certainly share structural and functional characteristics (9). Perhaps the most well-known function of globins is to reversibly bind oxygen for transport throughout the cardiovascular system. The term “globin” derives from a three-dimensional folding confirmation of the polypeptide that is constructed mainly of alpha helices. The globin-folded protein is non-covalently bound to a heme moiety consisting of a porphyrin (macrocyclic molecule) coordinated to a ferrous iron (Fe²⁺) in the center. The heme moiety is a chemically active group and needs to be surrounded by a hydrophobic environment, provided by the 3D globin fold, to retain its activity.

Hemoglobin (Hb) is a remarkable molecule. It is probably the most well-known globin and was one of the first protein structures determined by X-ray crystallography (10). The most common form of adult hemoglobin contains two polypeptides folded in the α form and two folded in the β form accompanied by a heme moiety to which oxygen (O₂) attaches via the ferrous iron. Each hemoglobin molecule can therefore carry four molecules of O₂, Hb₄O_8. The presence of hemoglobin in the blood increases its O₂-carrying capacity approximately 70-fold (11). When O₂ is not present, the globin units are tightly bound reducing the affinity for O₂. Upon binding of an oxygen molecule, there is a change in configuration which exposes the other oxygen binding sites, resulting in an increasing affinity of each heme for each subsequent O₂ molecule. This effect is represented by the oxygen–hemoglobin dissociation curve having a sigmoidal shape. To underscore the exquisite balance of structure and function, consider the fact that a single amino acid mutation in hemoglobin results in sickle-cell anemia.

What is of most relevance to BOLD contrast in NMR imaging is the amount of deoxyhemoglobin in the blood vessels of a given volume of tissue because it is paramagnetic thanks to the Fe²⁺ and lack of oxygen while oxyhemoglobin has a susceptibility approximately equal to the surrounding tissue. As the amount of deoxyhemoglobin increases in the blood vessels of a given volume of tissue, so too does the localized internal field which is experienced by surrounding spins. The ultimate result of this is a loss of signal intensity in that region of the NMR image due to loss of phase coherence amongst spins (Fig. 1).

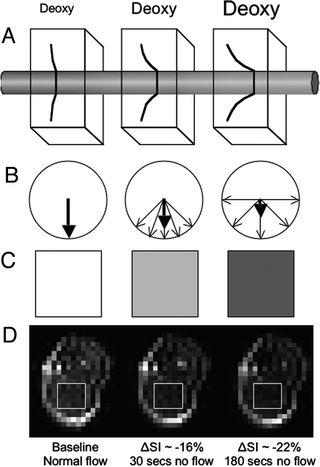
Fig. 1.

Graphical representation of the basic concept of BOLD contrast. (a) Increasing the amount of deoxyhemoglobin (deoxy) produces larger local magnetic field gradients around the blood vessel. (b) The larger the magnetic field gradients, the more the phase dispersion of nearby spins. (c) Greater phase dispersion results in greater loss in signal intensity in the NMR images. (d) Empirical example derived from quantifying the signal intensity in a region of interest centered in the gastrocnemius muscle of a mouse (rectangle) during normal blood flow and 30 s and 180 s after complete cessation of flow to the hindlimb by occluding the aorta and vena cava while the animal was in the magnet (see Chapter 27 or Greve et al. (38)).

2.2 Where Is the Source of Magnetic Susceptibility Found In Vivo?

Iron is the most abundant paramagnetic ion in the body with approximately 70% of it residing within hemoglobin (7) compartmentalized in red blood cells (RBCs; a.k.a. erythrocytes), which themselves are contained inside blood vessels along with plasma. The proportion of blood volume occupied by RBCs is defined by the metric hematocrit (Hct) which averages 40–50% in humans (11). RBCs are approximately 6–8 μm in diameter, 2 μm thick, and can contain approximately 280 million hemoglobin molecules (7). RBCs are more homogeneously distributed during bulk flow through large vessels but take on a single-file alignment when traversing capillaries and venules which have diameters similar to the RBCs themselves (12, 13). Deoxyhemoglobin is also spatially distributed along the length of the vascular network; hemoglobin in arterial blood is approximately 97% saturated with oxygen, while that in venous blood is about 75% saturated (11). The difference in magnetic susceptibility between tissue and blood that is approximately 60% saturated with oxygen has been estimated at 3 × 10⁻⁸ (14).

What is of most relevance to BOLD contrast in NMR imaging is the fact that the source of magnetic susceptibility in vivo, deoxyhemoglobin, has a very specific spatial distribution. It is compartmentalized intravascularly within the red blood cell and its basal level concentration depends on location along the vascular network. The water molecules residing within the RBCs, the plasma, and extravascularly all experience the paramagnetism of deoxyhemoglobin. To be explored in the next section are situations that alter the “what and where” of magnetic susceptibility (i.e., deoxyhemoglobin) in vivo, e.g., increases in blood flow that change the concentration of deoxyhemoglobin and the size of the vessel where the deoxyhemoglobin resides, respectively.

3 BOLD Contrast Generation

The aim of this section is to explain how alterations in the “what and where” of magnetic susceptibility in vivo alter the contrast in NMR images.

3.1 Things That Change the Amount of Deoxyhemoglobin

The factors that change the amount of deoxyhemoglobin are oxygen utilization, blood volume, blood flow. Similar to Norris (15), we will start by taking each parameter individually while holding the other two constant.

Increased oxygen utilization will increase the concentration of deoxyhemoglobin, increasing the amount of paramagnetic material present and local magnetic field inhomogeneity, thereby leading to a reduction in signal intensity in the NMR images.
Without changing the concentration of deoxyhemoglobin, increased blood volume will increase the total amount of paramagnetic material present and local magnetic field inhomogeneity, thereby leading to a reduction in signal intensity in the NMR images.
Increased blood flow will increase the washout of deoxyhemoglobin, decreasing the amount of paramagnetic material present and local magnetic field inhomogeneity, thereby leading to an increase in signal intensity in the NMR images.

Taken individually, things are simple enough. However, these parameters usually change concurrently. In fMRI experiments, for example, neuronal activation tends to increase all three. The local magnetic field increase resulting from O₂ utilization and increased blood volume is overcome by the local magnetic field decrease resulting from increased blood flow, resulting in an overall increase in signal intensity (16). Norris reflects the sentiment of the fMRI field when he describes the situation as a “near paradox” (15). Even Ogawa et al. originally hypothesized that “the active region could show darker lines in the image because of the increased level of deoxyhemoglobin resulting from higher oxygen consumption” (3). Although it is possible they were envisioning the “fast response” of the BOLD signal changes (beyond the scope of this chapter; for an excellent brief introduction see Buxton’s commentary (17)), it seems more likely they initially did not realize that increased blood flow would far surpass volume and O₂ utilization effects. This learning curve, even for the pioneers of the BOLD effect, is respectfully highlighted to emphasize the complicated nature of the physiology that underlies the contrast mechanism and buoy the confidence of novice imagers that time can provide clarity.

For the physiologists entering the NMR imaging realm, there is likely one more consideration in mind: changes in blood volume due to recruitment or vasodilation. Boxerman et al. (14) addressed BOLD signal changes due to recruitment as defined by increased number of perfused vessels or increased blood flow velocity through vessels. The focus of the latter was changes in RBC velocity through the capillaries and how that might affect the BOLD signal changes. Changes in R ₂ ^* and R ₂ linearly increased with physiologically relevant increases in blood volume. There was very little difference between whether the volume was increased due to recruitment (increased number of perfused vessels) or vasodilation. For recruitment as defined by increased blood flow/RBC velocity, changes in R ₂ ^* and R ₂ remained at the same level as those seen for typical velocities through the capillaries. It should also be noted that changes in R ₂ ^* and R ₂ calculated for typical RBC velocities through the capillaries are slightly smaller compared to models run with the non-physiologic situation of stationary RBCs. Macrovascular velocity effects were not studied due to more homogeneous distribution of RBCs during bulk flow through large vessels as mentioned above.

3.2 Things That Relate to the Localized Nature of Deoxyhemoglobin

Although deoxyhemoglobin is contained intravascularly within the RBCs, its field perturbations extend into the extravascular space, giving BOLD contrast an intravascular as well as an extravascular component.

3.2.1 Intravascular Relaxation Mechanisms

To begin the discussion of these two contributing components, it is worthwhile to remember that the contrast in MRI derives from water molecules and how their frequencies and phases are altered based on the magnetic field they experience locally. Therefore, we should begin by noting where the water molecules can reside:

(1)

Within the vessel in the plasma.

(2)

Within the vessel in the RBCs.

(3)

Extravascularly in the tissue.

There is a difference in magnetic susceptibility between the RBC and plasma itself. Therefore, one can imagine that spins contained within the RBC experience a different field compared to spins contained in the plasma. This simple idea becomes more complicated when one considers the fact that spins are not stationary. There are two options put forth to help conceptualize this last fact:

(1)

One can think of the signal loss resulting from the water molecules in the plasma diffusing through fields produced by the paramagnetic deoxyhemoglobin contained within the RBC.

(2)

Alternatively, one can think of the signal loss resulting from two-site exchange. Spins could be contained within an RBC or the plasma (experiencing the respective magnetic susceptibility) and then could exchange to the alternative compartment to experience a completely different magnetic susceptibility.

Modeling to explore each of these concepts has been performed (18).

A second intravascular component comes into focus with a slightly bigger picture view. A blood vessel containing some concentration of deoxyhemoglobin can be thought of as a cylinder made of a paramagnetic material. The frequency shift inside the cylinder depends on both the size of the cylinder and its orientation relative to the main field (4). This effect is important for larger vessels, radii > 10 μm, and is reduced when diffusion/two-site exchange is included in the model (4) (see Section 3.2.4). This frequency shift is a static mechanism, will be refocused during a spin echo acquisition, and therefore will not contribute to changes in R ₂.

3.2.2 Extravascular Relaxation Mechanisms

With regard to water exchange between either intravascular compartment (RBC or plasma) and the extravascular space, Boxerman et al. (14) showed virtually no effect on changes in R ₂ ^* or R ₂ whether the vessel was modeled as impermeable or with a level of permeability that is physiologically relevant. Although the model was not specific to the brain, per se, the argument of blood vessel impermeability may be due to the blood–brain barrier. Weisskoff (19) also notes this and follows with empirical evidence of the fact that there is no T ₁ enhancement in healthy brain tissue upon injection of non-blood-pool gadolinium agents. In organs where vascular permeability to water is higher (heart, kidney, muscle), it may contribute to the BOLD effect.

Beyond vessel permeability, what is important when considering extravascular relaxation mechanisms are the field gradients that extend into the extravascular space and diffusion of water molecules through these gradients. This will be discussed in more detail in the next section as it leads to the dependence of BOLD contrast on vessel size and pulse sequence.

3.2.3 Intra- vs. Extravascular Contributions to BOLD Contrast

Boxerman et al. (16) combined Monte Carlo simulations with an fMRI simulation emulating visual stimulation to assess the intravascular and extravascular contributions to signal changes on gradient echo images acquired at 1.5 T. They concluded from this work that approximately 2/3 of the change in signal intensity can be attributed to intravascular spins. They elegantly went on to emphasize this point empirically by acquiring fMRI data with and without diffusion gradients present that were set at values suitable to null signal from blood, thereby removing the intravascular contribution to signal changes that occur upon visual stimulation. In a similar manner, they observed that changes in signal intensity upon visual stimulation were reduced as diffusion weighting increased, thereby bolstering the notion that intravascular spins dominate gradient echo signal changes at 1.5 T. It should be noted that at higher field strengths, intravascular contributions become less important due to the fact that the T ₂ of blood is dramatically reduced (T ₂ of blood: 109–180 ms at 1.5 T; 6.7 ms at 7 T (15)).

3.2.4 Static Dephasing Regime vs. Motional Narrowing Regime

Blood vessel size and choice of sequence (gradient vs. spin echo) have an impact on the contrast in BOLD images. As mentioned above, extravascular relaxation mechanisms result from the static fields outside of the blood vessel caused by the intravascular deoxyhemoglobin and diffusion of extravascular spins through these fields (20). These mechanisms can largely be broken into static and diffusive regimes.

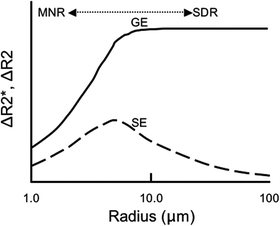
Initially ignoring diffusion of water, the magnetic fields that extend into the extravascular space give rise to a spatially dependent frequency shift that causes the accumulated phase of one spin to differ from that of its neighbor. The result is a loss of phase coherence in that voxel. Several groups have shown through modeling that this mechanism dominates for larger vessels (≥20 μm). It should be noted that this is a static mechanism, can be refocused during a spin echo acquisition, and therefore will not contribute to changes in R ₂. This is called the static dephasing regime (SDR) (20).

Diffusion becomes important when the random walk of a spin during the echo time is on the same order as the extent of the extravascular field gradients surrounding the blood vessel, i.e., approximately the radius of the vessel (15). In this situation, spins do not solely experience an increased or decreased field but instead experience a variety of fields throughout the echo time that depends on their particular path. The result is the same, viz., loss of phase coherence and hence a decrease in signal intensity on the NMR images. This mechanism is most important for vessels with radii of 6–8 μm (14). This mechanism is irreversible, will not be refocused during a spin echo acquisition, and therefore will contribute to changes in R ₂ and R ₂ ^*.

An additional consideration related to diffusion is when spins interchange position rapidly enough through the field gradients such that each spin, essentially, sees the same spread of frequencies, thereby accumulating approximately the same amount of phase, and maintaining some phase coherence resulting in smaller changes in signal intensity on BOLD images. This is called the motionally narrowed regime (MNR) (20).

Both vessel size and pulse sequence considerations are referred to in the above discussion. These effects are qualitatively summarized in Fig. 2, an adaptation from Boxerman, et al. (14) and Weisskoff et al. (19). One can see from Fig. 2 that changes in relaxation for gradient echo acquisitions (ΔR ₂ ^*) reach a plateau for vessel sizes greater than ∼10 μm. Changes in relaxation for spin echo acquisitions (ΔR ₂), however, have a maximum at ∼8 μm and decline for vessels smaller than (MNR) or larger than (SDR) this radius. Spin echo acquisitions are a specific reflection of the microvasculature while gradient echo sequences are overall more sensitive (i.e., changes in R ₂ ^* are larger than changes in R ₂ across all vessel sizes). As another means to emphasize the fact that BOLD data acquired via a spin echo or gradient echo sequence are weighted by the microvasculature and macrovasculature, respectively, models run varying the blood volume fraction composed of capillaries showed that changes in R ₂ ^* decreased by ∼1/3 as the model became solely composed of capillaries while changes in R ₂ were relatively unaffected for models composed of 40% capillaries or more (14). The focus on looking for a sequence and/or parameters that reflect changes in the microvasculature stems from the, not unfounded, hypothesis that microvascular changes are “a better reflection of localized neuronal activation” (14). In addition, gradient echo acquisitions depend more heavily on the experimental conditions and regional field properties, the latter of which can be dependent on shimming, for example. Therefore, although gradient echo acquisitions dominate the majority of BOLD investigations, it might be desirable to implement spin echo acquisitions especially at higher field strengths where some sensitivity can be regained.