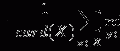Fig. 2.1
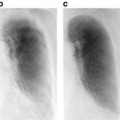
A mammogram image with suspected areas highlighted, and a magnified view of a region with clustered microcalcifications
Mammography currently provides the most effective strategy for early detection of breast cancer. The sensitivity of mammography could be up to approximately 90 % for patients without symptoms [2]. However, this sensitivity is highly dependent on the patient’s age, the size and conspicuity of the lesion, the hormonal status of the tumor, the density of a woman’s breasts, the overall image quality, and the interpretative skills of the radiologist [3]. Therefore, the overall sensitivity of mammography could range between from 90 to 70 % only [4]. Furthermore, it is very difficult to distinguish mammographically benign lesions from malignant ones. It has been estimated that one third of regularly screened women experience at least one false-positive (benign lesions being biopsied) screening mammogram over a period of 10 years [5]. A population-based study that included about 27,394 screening mammograms, which were interpreted by 1,067 radiologists showed that the radiologists had substantial variations in the false-positive rates ranging from 1.5 to 24.1 % [6]. Unnecessary biopsy is often cited as one of the risks of screening mammography. Surgical, needle-core, and fine-needle aspiration biopsies are expensive, invasive, and traumatic for the patient.
The last two decades have witnessed a great deal of research for developing computer-aided detection (CADe)/diagnosis (CADx) tools for detection and diagnosis of breast cancer [7–10]. This intensive research has resulted in several FDA approved commercial systems since the late 1990s, which aim to play the role of a virtual “second reader” by highlighting suspicious areas for further review by the radiologist in association with their own reading. Improvement in cancer detection and diagnosis has been reported in retrospective and prospective studies [11–13]. However, this was not without controversies [14]. A multi-institutional study of 43 facilities showed that the current CAD systems were associated with reduced accuracy of interpretation for screening mammograms [14]. In any case, these negative results may strongly urge the need for utilizing more improved techniques for analyzing mammogram images.
Content-based image retrieval (CBIR) may potentially provide new and exciting opportunities for the analysis and the interpretation of mammogram images. The underlying principle in CBIR is analogous to textual search engines (e.g., Google), in which a search engine aims to retrieve information that is relevant (or similar) to the user’s query. Instead of textual description, however, in CBIR the information is embedded in the form of an image or its extracted features. CBIR could serve as a diagnostic tool for aiding radiologists by comparing current cases with previously diagnosed ones in a medical archive.
In this chapter, we provide an overview of CBIR in recent years in the medical imaging literature and specifically for mammography. We discuss its expanding role and provide examples based on our experience using CBIR in mammography and highlight its strong potential as a valuable tool for computerized detection and diagnosis in mammography.
Background
Content-Based Image Retrieval
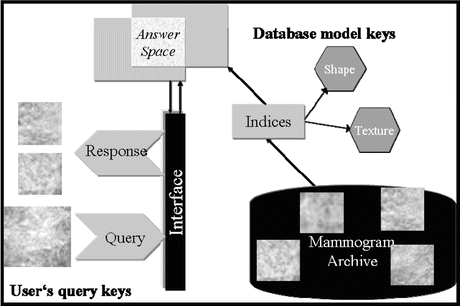
Image retrieval has been one of the most exciting and fastest growing research areas in image processing over the past decade [15]. There have been several general-purpose image retrieval systems developed. For instance, Guo et al. [16] developed a supervised approach for learning similarity measures for natural images, while Chen et al. [17] investigated unsupervised clustering-based image retrieval. Interested readers are referred to [15] for further examples on general-purpose CBIR systems. However, an evolving application of CBIR in recent years has been in the area of medical imaging [18]. CBIR has been developed as a visual-based approach to overcome some of the difficulties and problems associated with human perception subjectivity and annotation impreciseness in text-based retrieval systems. However, despite the significant developments over the past decade with respect to similarity measures, objective image interpretations, feature extraction, and semantic descriptors [18, 19], some fundamental difficulties still remain pertaining to CBIR applications. First, it is understood that similarity measures can vary with the different aspects of perceptual similarity between images; the selection of an appropriate similarity measure thus becomes problem-dependent. Second, the relation between the low-level visual features and the high-level human interpretation of similarity is not well defined when comparing two images; it is thus not exactly clear what features or combination of them are relevant for such judgment [20, 21]. Finally, while the user may understand more about the query, the database system can only guess (possibly through interactive learning) what the user is looking for during the retrieval process. This is an indispensable challenge in information retrieval, where the correct answer may not always be clearly identified. In Fig. 2.2, we show a diagram to illustrate a typical scenario of image retrieval from mammography databases, where an archive is organized into mammogram images, which in turn is organized into indices (i.e., a data structure of selected image features) for rapid lookup. The user formulates his/her retrieval problem as an expression in the query language (e.g., by presenting the images of the current case as query). The query is then translated into the language of indices and matched against those in the database, and those images with matching indices are retrieved.
CBIR as a CAD Tool
Historically, the concept of image retrieval in medical images was first introduced by Swett et al. [22], who developed a rudimentary, rule-based expert system to display radiographs from a library of images as illustrative examples for helping radiologists’ diagnosis. However, application of CBIR for medical images is a quite challenging task due to the complexity of image content in relation to the disease conditions. As a consequence, many of the useful image features in traditional CBIR are no longer adequate in medical imaging. For example, global image features (such as grayscale histogram) would not be salient for describing the characteristics of pathological regions or lesions which are typically localized in the images [18]. In such a case, it is important to derive quantitative features that correlate well with the anatomical or functional information perceived as important for diagnostic purposes by the physicians. Therefore, present medical CBIR systems mostly focus on a specific topic, thus offering support only for a restricted variety of image types and feature sets, such as high-resolution computed tomography (HRCT) scans of the lung [23]. This system was referred to as the ASSERT system, where a rich set of texture features was derived from the disease bearing regions. In [24], a new hierarchical approach to CBIR called “customized-queries” approach is applied to lung images. In [25], a system called CBIR2 was developed for retrieval of spine X-ray images. Three-dimensional MR image retrieval was studied in [26] based on anatomical structure matching. An online pathological neuroimage retrieval system was investigated in [27] under the framework of classification-driven feature selection. Cai et al. [28] presented a prototype design for content-based functional image retrieval for dynamic PET images. Tobin et al. [29] developed a CBIR system for retrieving diabetic retinopathy cases using a k-nearest neighbors (KNN)-based approach. Application to different medical databases such as dermatological images [30], cervicographic images [31], and microscopic pathology databases [32] was explored in the literature. More recently, there has also been growing interest in retrieving reference images from PACS, and CBIR has now become an important research direction in radiological sciences [18, 33, 34].
Despite the extensive research efforts in CBIR, current imaging standards such as DICOM v3.0 still rely on textual attributes of images (e.g., study, patient, and other parameters), which are still to date the only information used to select relevant images within PACS [35]. However, in recent years several research-oriented image retrieval projects and prototypes have been developed for management of medical images for research and teaching purposes. Examples of such systems include: the ASSERT mentioned above; CasImage [36], which retrieves a variety of images ranging from CT, MR, and radiographs to color photos based on color and textural features; IRMA (image retrieval in medical applications) [37], a development platform of components intended for CBIR in medical applications; NHANES II (the second national health and nutrition examination survey) [38] for retrieval of cervical and lumbar spine X-ray images based on the shape of the vertebra. In the rest of this chapter, we will focus on CBIR application to mammography due to its important role in breast cancer management.
Mammography
Mammograms are low-energy X-ray images of the breast of patients. Typically, they are in the order of 0.7 mSv. A mammogram can detect a cancerous or precancerous tumor in the breast even before the tumor is large enough to be palpable. The results are interpreted according to an American College of Radiology (ACR) score known as the Breast Imaging Reporting and Data System (BI-RADS™) with values ranging from 0 (incomplete) to 6 (known biopsy—proven malignancy) [39]. To date mammography remains the modality of choice for early screening of breast cancer. As mentioned earlier, there has been intensive development of CAD systems for computerized lesion detection; however, this was not without controversies about the value of such systems compared to human readers [14]. It is expected that human decision-making is much more complex than what a detection algorithm can provide. We share the belief that the potential value for application of CAD systems to mammography could be facilitated through the development of information systems based on CBIR.
CBIR for Mammography
Review of Existing Methods
Since the pioneering work by Swett et al. [22], there have been extensive efforts to apply CBIR to medical imaging in general and mammography in particular. Sklansky et al. [40] developed a technique that produces a two-dimensional (2D) map based on the decision space of a neural network classifier, in which images that are close to each other are selected for purposes of visualization; the neural network was trained for separating “biopsy recommended” and “biopsy not recommended” classes. Qi and Snyder [41] demonstrated the potential use of CBIR in PACS using a digital mammogram database based on the shape and size information of mass lesions. At about the same time, we started developing our perceptual similarity approach for retrieval of MC lesions in mammograms [42–44]. Giger et al. [45] developed an intelligent workstation interface that displays known malignant and benign cases similar to lesions in question (based on one or more selected features or computer estimated likelihood of malignancy), and demonstrated that radiologists’ performance, especially specificity, increases with the use of such aid tool. Tourassi et al. [46–48] developed an approach for retrieval and detection of masses in mammograms based on the use of information-theoretic measures (such as mutual information), where a decision index is calculated based on the query’s best matches. Zheng et al. [49] applied a KNN algorithm and further used observer-rated spiculation levels to improve the similarity of breast masses and subsequently investigated the use of mutual information [50] to improve the similarity measure. An unsupervised learning approach based on Kohonen self-organizing map (SOM) was proposed in [51]. The SOM was trained using a set of 88 features for each mammogram, which included common shape factors, texture, and moment features as well as angular projections and morphological features derived from segmented fibroglandular tissues.
As noted above, CBIR has been studied recently by researchers as a useful tool for exploring known cases from a reference library that can assist radiologists in diagnosis. The idea is to provide evidence for case-based reasoning with information from the retrieved cases [52]. As an indication of the predictive value of retrieved cases, the correlation in disease condition between the query and the retrieved cases was examined in previous work [21, 53]. The ratio of malignant cases among all retrieved cases was used as a useful predictor for the query [54, 55]; conceptually, this can be viewed as a KNN classifier using only the retrieved cases. The similarity level between a retrieved case and the query was used by Zheng et al. [49] as a weighting factor in the prediction. A genetic algorithm was used by Mazurowski et al. [56] to adjust the weighting factors of the retrieved cases. An observer study was used by Nakayama et al. [57] to investigate the potential diagnostic value of similar cases. These studies provide evidence on the positive predictive value of similar cases in CADx.
Evaluation Metrics
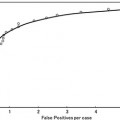
Retrieval systems are typically evaluated using the so-called precision-recall curves [58]. The retrieval precision is defined as the proportion of the images among all the retrieved that are truly relevant to a given query; the term recall is measured by the proportion of the images that are actually retrieved among all the relevant images to a query. Mathematically, they are given by:
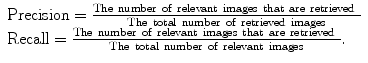
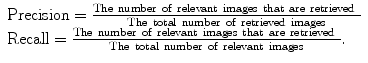
(2.1)
The precision-recall curve is a plot of the retrieval precision versus the recall over a continuum of the operating threshold. An example of precision-recall curves is given later in Fig. 2.4 in section “Case-Study Example.”
Other metrics to quantify the accuracy of a retrieval system could be defined on the similarity measure used, such as the mean-squared error (MSE) of the model score compared to the observer score. In addition, to evaluate the merit of the similarity measure for cancer diagnosis, criteria such as cumulative neighbor matching rate could be used [59]. In this case, for each query image, the ratio of top k images that actually match the disease condition of the query is computed and averaged over all the queries.
For statistical validation of the retrieval performance, resampling techniques such as cross-validation and bootstrap are typically used. In cross-validation, the data samples are divided into a number of subsets which are permuted for training and testing in a round-robin fashion, whereas in bootstrap, the data samples are randomly selected for training and testing for many times. Bootstrap could be regarded as a smoothed version of cross-validation. It is thought to be more realistic in modeling real life scenarios [60].
Finally, we add that besides these rather generic measures used in information retrieval, it is also necessary to evaluate the retrieval efficiency based on specific clinical tasks.
Example 1: Similarity Learning for CBIR
In this section, we present a CBIR application to mimic radiologists’ perceptual similarity using machine learning methods. As an example, we will consider in particular lesions with clustered MCs, which can be an important early sign of breast cancer in women. Their clustering patterns play an important role in determining malignancy risk following the BI-RADS criteria as mentioned in section “Mammography.”
Similarity as Nonlinear Regression Functional
In this approach, the notion of similarity is modeled as a nonlinear function of the image features in a pair of mammogram images containing lesions of interest, e.g., microcalcification clusters (MCCs). If we let vectors u and v denote the features of two MCCs at issue, the following regression model could be used to determine their similarity coefficient (SC):
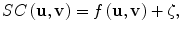
where f(u,v) is a function determined using a machine learning approach, which we choose to be support vector machine (SVM) learning [61], and ζ is the modeling error. The similarity function f(u,v) in Eq. (2.2) is trained using data samples collected in an observer study. For convenience, we denote f(u,v) by f(x) with x = [u T , v T ] T .
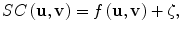
(2.2)
Assume that we have a set of N training samples, denoted by Z = {(x i ,y i )} i=1 N , where y i denotes the user similarity score for the MCC pair denoted by x i , i = 1, 2,…, N. The regression function f(x) is written in the following form:
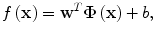
where Φ(x) is a mapping implicitly defined by a so-called kernel function which we introduce below. The parameters w and b in Eq. (2.3) are determined through minimization of the following structured risk:
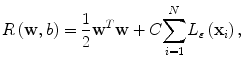
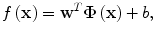
(2.3)
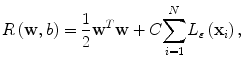
(2.4)
where L ε (•) is the so-called ε-insensitive loss function, which has the property that it does not penalize errors below the parameter ε. The constant C in Eq. (2.4) determines the trade-off between the model complexity and the training error. In this study the Gaussian radial basis function is used for the SVM kernel function K(⋅,⋅), where K(⋅,⋅) = Φ T (x)Φ(x). The regression function f(x) in Eq. (2.2) is characterized by a set of so-called support vectors:
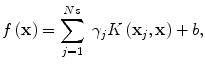
where x j are the support vectors and N s is the number of the support vectors.
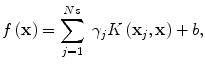
(2.5)
To model the similarity between two feature vectors, we want to learn a symmetric function satisfying f(u,v) = f(v,u), i.e., the notion of similarity is commutative. This can be achieved by duplicating the training image pairs, i.e., first with (u, v) and then with (v, u). We can explicitly enforce this property in the SVM cost function as:
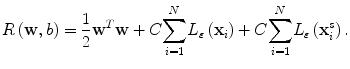
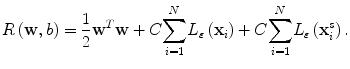
(2.6)
Here y(x i ) = y(x i s ), x i = (u i T , v i T ) T , x i s = (v i T , u i T ) T .
With this formulation the SVM training algorithm yields the global optimum of a symmetric Lagrangian. The resulting regression function can be written as:
![$$ f\left(\mathbf{x}\right)={\displaystyle \sum_{j=1}^{Ns}}\kern0.5em {\gamma}_j\left[K\left({\mathbf{x}}_j,\mathbf{x}\right)+K\left({\mathbf{x}}_j^s,\mathbf{x}\right)\right]+b. $$](/wp-content/uploads/2016/03/A218098_1_En_2_Chapter_Equ7.gif)
![$$ f\left(\mathbf{x}\right)={\displaystyle \sum_{j=1}^{Ns}}\kern0.5em {\gamma}_j\left[K\left({\mathbf{x}}_j,\mathbf{x}\right)+K\left({\mathbf{x}}_j^s,\mathbf{x}\right)\right]+b. $$](/wp-content/uploads/2016/03/A218098_1_En_2_Chapter_Equ7.gif)
(2.7)
That is, if a training sample x j is a support vector, i.e., |y j − f(x j )| ≥ ε, then its symmetric sample x j s is also a support vector and γ j = γ j s . This will ensure that the solution is symmetric: f(x) = f(x s ). A detailed proof of this is given in [59].